Solved papers for J & K CET Engineering J and K - CET Engineering Solved Paper-2007

done J and K - CET Engineering Solved Paper-2007 Total Questions - 225

• question_answer1) The only mechanical quantity which has negative dimension of mass is
  A)
   angular momentum
  done clear
  B)
   torque                                 
  done clear
  C)
   coefficient of thermal conductivity
  done clear
  D)
   gravitational constant
  done clear
  View Answer play_arrow

• question_answer2) Two vectors are given by \[\vec{A}=3\hat{i}+\hat{j}+3\hat{k}\]and \[\vec{B}=3\hat{i}+5\hat{j}-2\hat{k}\]. Find the third vector \[\vec{C},\] if \[\vec{A}+3\vec{B}-\vec{C}=\vec{0}\].
  A)
    \[12\hat{i}+14\hat{j}+12\hat{k}\]
  done clear
  B)
   \[13\hat{i}+17\hat{j}+12\hat{k}\]
  done clear
  C)
   \[12\hat{i}+16\hat{j}-3\hat{k}\]
  done clear
  D)
   \[15\hat{i}+13\hat{j}+4\hat{k}\]
  done clear
  View Answer play_arrow

• question_answer3) A particle moves from position \[3\hat{i}+2\hat{j}+6\hat{k}\] to \[14\hat{i}+13\hat{j}+9\hat{k}\] due to a uniform force of\[4\hat{i}+\hat{j}+3k\text{ }N\]. Find the work done, if the displacement is in metre.
  A)
   \[16\text{ }J\]         
  done clear
  B)
   \[64\text{ }J\]
  done clear
  C)
   \[32\text{ }J\]         
  done clear
  D)
   \[48\text{ }J\]
  done clear
  View Answer play_arrow

• question_answer4) The coordinates of a moving particle at any time t are given by \[x=\alpha {{t}^{3}}\]and \[y=\beta {{t}^{3}}\]. The speed of the particle at time t is given by
  A)
   \[3t\,\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\]   
  done clear
  B)
   \[3{{t}^{2}}\,\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\]
  done clear
  C)
   \[{{t}^{2}}\,\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\]
  done clear
  D)
   \[\,\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer5) A body is moving with uniform acceleration. covers \[200\text{ }m\]in the first \[2\text{ }s\]and \[220\text{ }m\]in the next\[4\text{ }s\] . Find the velocity in m/s after\[7\text{ }s\].
  A)
   \[10\]           
  done clear
  B)
   \[15\]
  done clear
  C)
   \[20\]           
  done clear
  D)
   \[30\]
  done clear
  View Answer play_arrow

• question_answer6) From the top of a tower a body A is projected vertically up, another body B is horizontally thrown and a third body C is thrown vertically down with same velocity. Then
  A)
   B strikes the ground with more velocity
  done clear
  B)
   C strikes the ground with less velocity
  done clear
  C)
   A,B,C strike the ground with same velocity
  done clear
  D)
   A and C strike the ground with more velocity than B
  done clear
  View Answer play_arrow

• question_answer7) A body is released from a great height falls freely towards the earth. Another body is released from the same height exactly a second latter. Then the separation between two bodies, 2 s after the release of the second body is, nearly
  A)
   \[15\,\,m\]        
  done clear
  B)
   \[20\,\,m\]
  done clear
  C)
   \[25\,\,m\]         
  done clear
  D)
   \[30\,\,m\]
  done clear
  View Answer play_arrow

• question_answer8) A body of mass \[10\text{ }kg\]is acted upon by two forces each of magnitude \[10\,\,N\]making an angle of \[{{60}^{o}}\] with each other. Find the net acceleration of the body.
  A)
   \[2\sqrt{3}m/{{s}^{2}}\]    
  done clear
  B)
    \[\sqrt{3}m/{{s}^{2}}\]
  done clear
  C)
   \[3\sqrt{3}m/{{s}^{2}}\]    
  done clear
  D)
    \[4\sqrt{3}m/{{s}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer9) A body of mass \[{{m}_{1}}\] collides elastically with another body of mass \[{{m}_{2}}\] at rest. If the velocity of \[{{m}_{1}}\] after collision becomes \[2/3\] times its initial velocity, the ratio of their masses, is
  A)
   \[1:5\]         
  done clear
  B)
   \[5:1\]
  done clear
  C)
   \[5:2\]         
  done clear
  D)
   \[2:5\]
  done clear
  View Answer play_arrow

• question_answer10) With increase of temperature, the frictional force acting between two surfaces
  A)
   increases
  done clear
  B)
   remains the same
  done clear
  C)
   decreases
  done clear
  D)
   becomes zero
  done clear
  View Answer play_arrow

• question_answer11) The motion of the centre of mass is the result of
  A)
   internal forces                         
  done clear
  B)
   external forces
  done clear
  C)
   attractive forces                             
  done clear
  D)
   repulsive forces
  done clear
  View Answer play_arrow

• question_answer12) A stationary bomb explodes into two parts of masses in the ratio of \[1:3\]. If the heavier mass moves with a velocity \[4\text{ }m/s,\] what is the velocity of lighter part?
  A)
   \[12\text{ }m{{s}^{-1}}\]opposite to heavier mass
  done clear
  B)
   \[12\text{ }m{{s}^{-1}}\] in the direction of heavier mass
  done clear
  C)
   \[\text{6 }m{{s}^{-1}}\] opposite to heavier mass
  done clear
  D)
   \[\text{6 }m{{s}^{-1}}\] in the direction of heavier mass
  done clear
  View Answer play_arrow

• question_answer13) A body is tied to one end of the string and whirled in a vertical circle, the physical quantity which remains constant is
  A)
   momentum   
  done clear
  B)
   speed
  done clear
  C)
   kinetic energy
  done clear
  D)
   total energy
  done clear
  View Answer play_arrow

• question_answer14) A thin metal disc of radius of \[0.25\text{ }m\]and mass \[2\text{ }kg\]starts from rest and rolls down on an inclined plane. If its rotational kinetic energy is \[4\text{ }J\]at the foot of inclined plane, then the linear velocity at the same point, is in m/s
  A)
   \[2\]            
  done clear
  B)
   \[2\sqrt{2}\]
  done clear
  C)
   \[2\sqrt{3}\]          
  done clear
  D)
   \[3\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer15) A stone tied to one end of rope and rotated in a circular motion. If the string suddenly breaks, then the stone travels
  A)
   in perpendicular direction
  done clear
  B)
   in direction of centrifugal force
  done clear
  C)
   towards centripetal force
  done clear
  D)
   in tangential direction
  done clear
  View Answer play_arrow

• question_answer16) The escape velocity of a body from the earth is \[{{v}_{e}}\]. If the radius of earth contracts to \[\frac{1}{4}th\] of its value, keeping the mass of the earth constant, the escape velocity will be
  A)
   doubled      
  done clear
  B)
   halved
  done clear
  C)
   tripled        
  done clear
  D)
   unaltered
  done clear
  View Answer play_arrow

• question_answer17) The-radius of the earth is R. The height of a point vertically above the earth's surface at which acceleration due to gravity becomes \[1%\] of its value at the surface is
  A)
   \[8\,\,R\]          
  done clear
  B)
   \[9\,\,R\]
  done clear
  C)
   \[10\,\,R\]         
  done clear
  D)
   \[20\,\,R\]
  done clear
  View Answer play_arrow

• question_answer18) A heavy uniform rod is hanging vertically from a fixed support. It is stretched by its own weight. The diameter of the rod is
  A)
   smallest at the top and gradually increases down the rod
  done clear
  B)
   largest at the top and gradually decreases down the rod
  done clear
  C)
   uniform everywhere
  done clear
  D)
   maximum in the middle
  done clear
  View Answer play_arrow

• question_answer19) A particular force (F) applied on a wire increases its length by \[2\times {{10}^{-3}}\text{ }m\]. To increase the wire's length by \[4\times {{10}^{-3}}\text{ }m\]the applied force will be             
  A)
   \[4\,\,F\]           
  done clear
  B)
   \[3\,\,F\]
  done clear
  C)
   \[2\,\,F\]           
  done clear
  D)
   \[F\]
  done clear
  View Answer play_arrow

• question_answer20) The meniscus of mercury in a capillary glass tube, is
  A)
   concave      
  done clear
  B)
   plane
  done clear
  C)
   cylindrical    
  done clear
  D)
   convex
  done clear
  View Answer play_arrow

• question_answer21) Two liquid drops have diameters of \[1\text{ }cm\]and \[1.5\text{ }cm\] The ratio of excess of pressures inside them is
  A)
   \[1:1\]        
  done clear
  B)
   \[5:3\]
  done clear
  C)
   \[2:3\]        
  done clear
  D)
   \[3:2\]
  done clear
  View Answer play_arrow

• question_answer22) Temperature remaining constant, the pressure of gas is decreased by \[20%\]. The percentage change in volume
  A)
   increases by \[20%\]
  done clear
  B)
   decreases by \[20%\]
  done clear
  C)
   increases by \[25%\]
  done clear
  D)
   decreases by \[25%\]
  done clear
  View Answer play_arrow

• question_answer23) Work done in converting one gram of ice at \[-{{10}^{o}}C\]into steam at \[{{100}^{o}}C\]is
  A)
   \[3045\text{ }J\]       
  done clear
  B)
   \[6056\text{ }J\]
  done clear
  C)
   \[721\text{ }J\]        
  done clear
  D)
   \[616\text{ }J\]
  done clear
  View Answer play_arrow

• question_answer24) The temperature of the system decreases in the process of
  A)
   free expansion
  done clear
  B)
   adiabatic expansion
  done clear
  C)
   isothermal expansion
  done clear
  D)
   isothermal compression
  done clear
  View Answer play_arrow

• question_answer25) The temperature at which a black body ceases to radiate energy, is
  A)
   \[0\,\,K\]          
  done clear
  B)
   \[273\text{ }K\]
  done clear
  C)
   \[30\text{ }K\]         
  done clear
  D)
   \[100\text{ }K\]
  done clear
  View Answer play_arrow

• question_answer26) A particle executes SHM with a period of \[8\text{ }s\]and amplitude \[4\text{ }cm\]. Its maximum speed in cm/s, is
  A)
   \[\pi \]              
  done clear
  B)
   \[\frac{\pi }{2}\]
  done clear
  C)
   \[\frac{\pi }{3}\]
  done clear
  D)
   \[\frac{\pi }{4}\]
  done clear
  View Answer play_arrow

• question_answer27) The displacement of a particle of mass \[3\text{ }g\] executing simple harmonic motion is given by \[Y=3\text{ }sin\text{ (}0.2\text{ t)}\]in SI units. The KE of the particle at a point which is at a distance equal to \[1/3\] of its amplitude from its mean position is
  A)
   \[12\times {{10}^{-3}}\,J\] 
  done clear
  B)
   \[25\times {{10}^{-3}}\,J\]
  done clear
  C)
   \[0.48\times {{10}^{-3}}\,J\]  
  done clear
  D)
   \[0.24\times {{10}^{-3}}\,J\]
  done clear
  View Answer play_arrow

• question_answer28) A uniform spring of force constant k is cut into two pieces whose lengths are in the ratio of \[1:2\]. What is the force constant of second piece in terms of k?
  A)
   \[\frac{k}{2}\]
  done clear
  B)
   \[\frac{2k}{2}\]
  done clear
  C)
   \[\frac{3k}{2}\]
  done clear
  D)
   \[\frac{4k}{2}\]
  done clear
  View Answer play_arrow

• question_answer29) A girl swings on cradle in a sitting position. If she stands what happens to the time period of girl and cradle?
  A)
   Time period decreases
  done clear
  B)
   Time period increases
  done clear
  C)
   Remains constant
  done clear
  D)
   First increases and then remains constant
  done clear
  View Answer play_arrow

• question_answer30) The intensity ratio of two waves is \[1:9\]. The ratio of their amplitudes, is
  A)
   \[3:1\]        
  done clear
  B)
   \[1:3\]
  done clear
  C)
   \[1:9\]        
  done clear
  D)
   \[9:1\]
  done clear
  View Answer play_arrow

• question_answer31) The speed of sound waves in a gas
  A)
   does not depend upon density of the gas
  done clear
  B)
   'does not depend upon changes in pressure
  done clear
  C)
   does not depend upon temperature
  done clear
  D)
   depends upon density of the gas
  done clear
  View Answer play_arrow

• question_answer32) A segment of wire vibrates with fundamental frequency of \[450\text{ }Hz\]under a tension of\[9\text{ }kg-wt\]. Then tension at which the fundamental frequency of the same wire becomes \[900\text{ }Hz\]is
  A)
   \[36\text{ }kg-wt\]     
  done clear
  B)
   \[27\text{ }kg-wt\]
  done clear
  C)
   \[18\text{ }kg-wt\]     
  done clear
  D)
   \[72\text{ }kg-wt\]
  done clear
  View Answer play_arrow

• question_answer33) Sound waves in air cannot be polarized because
  A)
    their speed is small
  done clear
  B)
   they require medium
  done clear
  C)
   these are longitudinal
  done clear
  D)
   their speed is temperature dependent
  done clear
  View Answer play_arrow

• question_answer34) Electric potential at the centre of a charged hollow metal sphere is
  A)
   zero
  done clear
  B)
   twice as that on the surface
  done clear
  C)
   half of that on the surface
  done clear
  D)
   same as that on the surface
  done clear
  View Answer play_arrow

• question_answer35) Three charges \[1\mu C,\] \[1\mu C\] and \[2\mu C\] are kept at vertices of A, B and C of an equilateral triangle ABC of \[10\text{ }cm\]side respectively. The resultant force on the charge at C is
  A)
   \[0.9\text{ }N\]         
  done clear
  B)
   \[1.8\text{ }N\]
  done clear
  C)
   \[2.72\text{ }N\]
  done clear
  D)
   \[3.12\text{ }N\]
  done clear
  View Answer play_arrow

• question_answer36) A dielectric of dielectric constant K is introduced such that half of its area of a capacitor of capacity C is occupied by it. The new capacity is
  A)
   \[2\,C\]          
  done clear
  B)
   \[C/2\]
  done clear
  C)
   \[(1+K)C/2\]   
  done clear
  D)
   \[2C(1+K)\]
  done clear
  View Answer play_arrow

• question_answer37) The value equal to the velocity of light in vacuum is
  A)
   \[\frac{\sqrt{{{\mu }_{0}}}}{{{\varepsilon }_{0}}}\]
  done clear
  B)
   \[\frac{1}{\sqrt{{{\mu }_{0}}{{\varepsilon }_{0}}}}\]
  done clear
  C)
   \[\sqrt{{{\mu }_{0}}\,{{\varepsilon }_{0}}}\]
  done clear
  D)
   \[\sqrt{\frac{{{\mu }_{0}}}{\,{{\varepsilon }_{0}}}}\]
  done clear
  View Answer play_arrow

• question_answer38) Two unlike charges of the same magnitude Q are placed at a distance d. The intensity of the electric field at the middle point in the line joining the two charges
  A)
   zero         
  done clear
  B)
   \[\frac{8\,Q}{4\pi {{\varepsilon }_{0}}{{d}^{2}}}\]
  done clear
  C)
   \[\frac{6\,Q}{4\pi {{\varepsilon }_{0}}{{d}^{2}}}\]
  done clear
  D)
   \[\frac{4\,Q}{4\pi {{\varepsilon }_{0}}{{d}^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer39) In a meter bridge experiment, the ratio of the left gap resistance to right gap resistance is \[2:3,\] the balance point from left is
  A)
   \[60\text{ }cm\]       
  done clear
  B)
   \[50\text{ }cm\]
  done clear
  C)
   \[40\text{ }cm\]        
  done clear
  D)
   \[20\text{ }cm\]
  done clear
  View Answer play_arrow

• question_answer40) The  physical  quantity in  electrostatics analogous to temperature in heat is
  A)
   heat energy   
  done clear
  B)
   capacity
  done clear
  C)
   resistance     
  done clear
  D)
   potential
  done clear
  View Answer play_arrow

• question_answer41) If the electric current through an electric bulb is \[3.2\text{ }A,\] the number of electrons flow through it in one second is
  A)
   \[2\times {{10}^{9}}\]       
  done clear
  B)
   \[2\times {{10}^{19}}\]
  done clear
  C)
   \[3.2\times {{10}^{19}}\]     
  done clear
  D)
   \[1.6\times {{10}^{18}}\]
  done clear
  View Answer play_arrow

• question_answer42) A wire P has a resistance of \[20\,\Omega \]. Another wire Q of same material but length twice that of P has resistance of \[8\,\,\,\Omega \]. If r is the radius of cross-section of P, the radius of cross-section of Q is
  A)
   \[r\]
  done clear
  B)
   \[\frac{r}{\sqrt{2}}\]
  done clear
  C)
   \[\sqrt{5}\,r\]
  done clear
  D)
   \[2\,r\]
  done clear
  View Answer play_arrow

• question_answer43) When a metal conductor connected to the left gap of a meter bridge is heated, the balancing point
  A)
   shifts towards right
  done clear
  B)
   shifts towards left
  done clear
  C)
   remains unchanged
  done clear
  D)
   remains at zero
  done clear
  View Answer play_arrow

• question_answer44) The thermocouple among the following that can produce maximum thermo emf for the same temperature difference between the junction is
  A)
   \[Fe-Cu\]        
  done clear
  B)
  \[Ag-Au\]
  done clear
  C)
  \[Sb-Bi\]        
  done clear
  D)
   \[Cu-Pb\]
  done clear
  View Answer play_arrow

• question_answer45) A bar magnet of magnetic moment At and moment of inertia I is freely suspended such that the magnetic axial line is in the direction of magnetic meridian. If the magnet is displaced by a very small angle \[\theta ,\] angular acceleration is (magnetic induction of earth's horizontal field \[={{B}_{H}}\])
  A)
   \[\frac{M{{B}_{H}}\theta }{I}\]
  done clear
  B)
   \[\frac{I{{B}_{H}}\theta }{M}\]
  done clear
  C)
   \[\frac{M\theta }{I{{B}_{H}}}\]
  done clear
  D)
   \[\frac{I\theta }{M{{B}_{H}}}\]
  done clear
  View Answer play_arrow

• question_answer46) A long magnet is cut into two equal parts, such that the length of each half is same as that of original magnet. If the period of original magnet is T, the period of new magnet is
  A)
   \[T\]              
  done clear
  B)
   \[\frac{T}{2}\]
  done clear
  C)
   \[\frac{T}{4}\]            
  done clear
  D)
   \[2T\]
  done clear
  View Answer play_arrow

• question_answer47) The time period of a freely suspended bar magnet in a field is 2 s. It is cut into two equal parts along its axis, (hen the time period is
  A)
   \[4\,\,s\]          
  done clear
  B)
   \[0.5\,\,s\]
  done clear
  C)
   \[2\,\,s\]          
  done clear
  D)
   \[0.25\,\,s\]
  done clear
  View Answer play_arrow

• question_answer48) The angle between magnetic meridian and geographical meridian is known as
  A)
   magnetic dip
  done clear
  B)
   magnetic latitude
  done clear
  C)
   magnetic declination
  done clear
  D)
   magnetic longitude
  done clear
  View Answer play_arrow

• question_answer49) The net magnetic flux through any closed surface, kept in a magnetic field is
  A)
   zero          
  done clear
  B)
   \[\frac{{{\mu }_{0}}}{4\pi }\]
  done clear
  C)
   \[4\,\,\pi {{\mu }_{0}}\]        
  done clear
  D)
   \[\frac{4\,\,{{\mu }_{0}}}{\pi }\]
  done clear
  View Answer play_arrow

• question_answer50) A paramagnetic liquid is taken in a U-tube and arranged so that one of its limbs is kept between pole pieces of the magnet. The liquid level in the limb
  A)
   goes down
  done clear
  B)
   rises up
  done clear
  C)
   remains same
  done clear
  D)
   first goes down and then rises
  done clear
  View Answer play_arrow

• question_answer51) Two wires A and B are of lengths \[40\text{ }cm\]and\[30\text{ }cm\]. A is bent into a circle of radius r and B into an arc of radius r. A current \[{{i}_{1}}\] is passed through A and 13 through B. To have the same magnetic inductions at the centre, the ratio of \[{{i}_{1}}:{{i}_{2}}\] is
  A)
   \[3:4\]      
  done clear
  B)
   \[3:5\]
  done clear
  C)
   \[2:3\]       
  done clear
  D)
   \[4:3\]
  done clear
  View Answer play_arrow

• question_answer52) An electron and proton having same kinetic energy enter into magnetic field perpendicular to it. Then
  A)
   the path of electron is less curved
  done clear
  B)
   the path of proton is less curved
  done clear
  C)
   both have equal curved paths
  done clear
  D)
   both have straight line paths
  done clear
  View Answer play_arrow

• question_answer53) Two free parallel wires carrying currents in the opposite directions
  A)
   attract each other
  done clear
  B)
   repel each other
  done clear
  C)
   do not effect each other
  done clear
  D)
   get rotated to be perpendicular to each other
  done clear
  View Answer play_arrow

• question_answer54) A circular coil of diameter \[21\text{ }cm\]is placed in a magnetic field of induction\[{{10}^{-4}}\text{ }T\]. The magnitude of flux linked with coil when the plane of coil makes an angle \[{{30}^{o}}\] with the field is
  A)
   \[1.44\times {{10}^{-6}}\,Wb\]
  done clear
  B)
   \[1.732\times {{10}^{-6}}\,\,Wb\]
  done clear
  C)
   \[3.1\times {{10}^{-6}}\,\,Wb\]
  done clear
  D)
   \[4.2\times {{10}^{-6}}\,\,Wb\]
  done clear
  View Answer play_arrow

• question_answer55) The cladding material of optical fibres has refractive index
  A)
   greater than that of core
  done clear
  B)
   infinity
  done clear
  C)
   equal to that of core
  done clear
  D)
   less than that of core
  done clear
  View Answer play_arrow

• question_answer56) Red colour is used for danger signals because
  A)
   it causes fear
  done clear
  B)
   it undergoes least scattering
  done clear
  C)
   it undergoes maximum scattering
  done clear
  D)
   it is in accordance with international convention
  done clear
  View Answer play_arrow

• question_answer57) The least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is \[1.5\]. Then the angle of prism is
  A)
   \[2\,{{\cos }^{-1}}\left( \frac{3}{4} \right)\]
  done clear
  B)
   \[si{{n}^{-1}}\left( \frac{3}{4} \right)\]
  done clear
  C)
   \[2\,\,si{{n}^{-1}}\left( \frac{3}{2} \right)\]
  done clear
  D)
   \[{{\cos }^{-1}}\left( \frac{3}{2} \right)\]
  done clear
  View Answer play_arrow

• question_answer58) In a spectrometer experiment the prisms A, B, C with same angle but different refractive index \[{{\mu }_{A}}=1.33,\,\,{{\mu }_{B}}=1.5,\,\,{{\mu }_{C}}=1.44\]are used. The corresponding angles of minimum deviation \[{{D}_{A}},\,{{D}_{B}},\,{{D}_{C}}\] measured will be such that
  A)
   \[{{D}_{A}}>\,{{D}_{B}}>\,{{D}_{C}}\]
  done clear
  B)
   \[{{D}_{A}}<\,{{D}_{B}}<\,{{D}_{C}}\]
  done clear
  C)
   \[{{D}_{A}}<\,{{D}_{C}}<\,{{D}_{B}}\]
  done clear
  D)
   \[{{D}_{A}}>\,{{D}_{C}}>\,{{D}_{B}}\]
  done clear
  View Answer play_arrow

• question_answer59) Young's double slit experiment arrangement is shifted from air to water medium, the fringe width
  A)
   increases
  done clear
  B)
   decreases
  done clear
  C)
   becomes infinite
  done clear
  D)
   remains the same
  done clear
  View Answer play_arrow

• question_answer60) On introducing a thin film in the path of one of the two interfering beams, the central fringe will shift by one fringe width. If \[\mu =1.5,\] the thickness of the film is (wavelength of monochromatic light is \[\lambda \])
  A)
   \[4\,\lambda \]           
  done clear
  B)
   \[3\,\lambda \]
  done clear
  C)
   \[2\,\lambda \]           
  done clear
  D)
   \[\lambda \]
  done clear
  View Answer play_arrow

• question_answer61) The critical angle of the medium with respect to vacuum is \[{{30}^{o}}\]. If the velocity of light in vacuum is \[3\times {{10}^{8}}\text{ }m{{s}^{-1}},\] the velocity of light in medium is
  A)
   \[2\times {{10}^{8}}\text{ }m{{s}^{-1}}\]  
  done clear
  B)
   \[1.5\times {{10}^{8}}\text{ }m{{s}^{-1}}\]
  done clear
  C)
   \[3\times {{10}^{8}}\text{ }m{{s}^{-1}}\] 
  done clear
  D)
   \[\sqrt{2}\times {{10}^{8}}\text{ }m{{s}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer62) The distance between the first dark and bright band formed in Young's double slit experiment with band width B is
  A)
   \[\frac{B}{4}\]
  done clear
  B)
   \[B\]
  done clear
  C)
   \[\frac{B}{2}\]
  done clear
  D)
   \[\frac{3B}{2}\]
  done clear
  View Answer play_arrow

• question_answer63) The important conclusion given by Millikan's experiment about the charge is
  A)
   charge is never quantized
  done clear
  B)
   charge has no definite value
  done clear
  C)
   charge is quantized
  done clear
  D)
   charge on oil drop always increases
  done clear
  View Answer play_arrow

• question_answer64) An electron is accelerated through a potential difference of V volts. The speed of electrons will be
  A)
   \[\sqrt{\frac{eV}{m}}\]
  done clear
  B)
   \[\sqrt{\frac{2eV}{m}}\]
  done clear
  C)
   \[\sqrt{\frac{eV}{2m}}\]
  done clear
  D)
   \[\sqrt{\frac{m}{2eV}}\]
  done clear
  View Answer play_arrow

• question_answer65) How many photons are emitted by a laser source of \[5\times {{10}^{-3}}W\]operating at \[632.2\text{ }nm\]in \[2s\]?
  A)
   \[3.2\times {{10}^{16}}\]    
  done clear
  B)
   \[1.6\times {{10}^{16}}\]
  done clear
  C)
   \[4\times {{10}^{16}}\]     
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer66) If a is radius of first Bohr orbit in hydrogen atom, the radius of the third orbit is
  A)
   \[3a\]           
  done clear
  B)
   \[9a\]
  done clear
  C)
   \[27a\]          
  done clear
  D)
   \[81a\]
  done clear
  View Answer play_arrow

• question_answer67) Nuclear fission can be explained based on
  A)
   Millikan's oil drop method
  done clear
  B)
   Liquid drop model
  done clear
  C)
   Shell model
  done clear
  D)
   Buffs model
  done clear
  View Answer play_arrow

• question_answer68) The radius of a nucleus with atomic mass number 7 is 2 Fermi. Find the radius of nucleus with atomic number 189.
  A)
   3 Fermi      
  done clear
  B)
   4 Fermi
  done clear
  C)
   5 Fermi      
  done clear
  D)
   6 Fermi
  done clear
  View Answer play_arrow

• question_answer69) As mass number increases, surface area
  A)
   decreases
  done clear
  B)
   increases
  done clear
  C)
   remains the same
  done clear
  D)
   remains the same and increases
  done clear
  View Answer play_arrow

• question_answer70) All nucleons in an atom are held by      
  A)
   nuclear forces
  done clear
  B)
   van der Waals' forces
  done clear
  C)
   tensor forces
  done clear
  D)
   Coulomb forces
  done clear
  View Answer play_arrow

• question_answer71) The temperature of germanium is decreased from room temperature to \[100\text{ }K,\]the resistance of germanium
  A)
   decreases
  done clear
  B)
   increases
  done clear
  C)
   unaffected
  done clear
  D)
   depends on external conditions
  done clear
  View Answer play_arrow

• question_answer72) The potential in depletion layer is due to
  A)
   electrons
  done clear
  B)
   holes
  done clear
  C)
   ions
  done clear
  D)
   forbidden band
  done clear
  View Answer play_arrow

• question_answer73) In breakdown region, a zener diode behaves as a
  A)
   constant current source
  done clear
  B)
   constant voltage source
  done clear
  C)
   constant resistance source
  done clear
  D)
   constant power source
  done clear
  View Answer play_arrow

• question_answer74) When boron is added as an impurity to silicon, the resulting material is
  A)
   n-type semiconductor
  done clear
  B)
   n-type conductor
  done clear
  C)
   p -type conductor 
  done clear
  D)
   p -type semiconductor
  done clear
  View Answer play_arrow

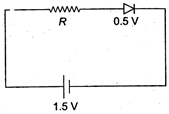
• question_answer75) The diode used in the circuit shown in the figure has a constant voltage drop of \[0.5\text{ }V\]at all currents and a maximum power rating of 100 milli-watt. What should be the value of the resistance R, connected in series with the diode, for obtaining maximum current?
  A)
   \[1.5\,\Omega \]
  done clear
  B)
   \[5\,\Omega \]
  done clear
  C)
   \[6.67\,\,\Omega \]
  done clear
  D)
   \[200\]
  done clear
  View Answer play_arrow

• question_answer76) The presence of electric charge on colloidal particles is indicated by the property, called
  A)
   dialysis       
  done clear
  B)
   solubility
  done clear
  C)
   electrophoresis
  done clear
  D)
   osmosis
  done clear
  View Answer play_arrow

• question_answer77) The protective action of different lyophilic colloids is expressed in terms of
  A)
   oxidation number
  done clear
  B)
   atomic number
  done clear
  C)
   Avogadro number
  done clear
  D)
   gold number
  done clear
  View Answer play_arrow

• question_answer78) The group of elements in which the differentiating electrons  enters  in  the antipenultimate shell of atoms are called
  A)
   \[f-\]block elements   
  done clear
  B)
  \[p-\]block elements
  done clear
  C)
   \[s-\]block elements   
  done clear
  D)
   \[d-\]block elements
  done clear
  View Answer play_arrow

• question_answer79) Lanthanides and actinides are also called as
  A)
   short periods
  done clear
  B)
   inner-transition elements
  done clear
  C)
   long periods
  done clear
  D)
   main transition elements
  done clear
  View Answer play_arrow

• question_answer80) The geometrical shape of \[s{{p}^{3}}d\]hybridisation is
  A)
   linear
  done clear
  B)
   trigonal bipyramid
  done clear
  C)
   square planar
  done clear
  D)
   tetrahedral
  done clear
  View Answer play_arrow

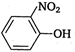
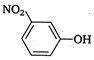
• question_answer81) Intermolecular hydrogen bonding exists in
  A)
  \[~o-\] nitrophenol
  done clear
  B)
   \[~o-\]chlorophenol
  done clear
  C)
   water
  done clear
  D)
   ammonium chloride
  done clear
  View Answer play_arrow

• question_answer82) Which one of the following examples exhibit transient existence?
  A)
   H            
  done clear
  B)
   \[H_{2}^{+}\]
  done clear
  C)
  \[{{H}^{+}}\]           
  done clear
  D)
   He
  done clear
  View Answer play_arrow

• question_answer83) The number of covalent bonds in fluorine molecule is
  A)
   2              
  done clear
  B)
   3
  done clear
  C)
   1              
  done clear
  D)
   5
  done clear
  View Answer play_arrow

• question_answer84) Carbon shows the following oxidation state a its hydrides
  A)
   + 1        
  done clear
  B)
   + 4
  done clear
  C)
   + 2         
  done clear
  D)
   + 3
  done clear
  View Answer play_arrow

• question_answer85) The following is not an example of oxyacids of sulphur
  A)
  \[{{H}_{2}}S{{O}_{3}}\]
  done clear
  B)
  \[{{H}_{2}}{{S}_{2}}{{O}_{3}}\]
  done clear
  C)
   \[{{H}_{2}}S{{O}_{4}}\]
  done clear
  D)
  \[S{{O}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer86) Calcium sulphate is sparingly soluble in
  A)
   water        
  done clear
  B)
   alcohol
  done clear
  C)
   acetic acid    
  done clear
  D)
   benzene
  done clear
  View Answer play_arrow

• question_answer87) The bleaching action of chlorine is due to the liberation of the following
  A)
  \[HOCl\]
  done clear
  B)
   \[HCl\]
  done clear
  C)
   \[[O]\]
  done clear
  D)
  \[{{O}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer88) The colour of transition metal ions is due to presence of unpaired electron transitions in available empty electron in
  A)
   \[d-\]orbitals
  done clear
  B)
   \[p-\]orbitals
  done clear
  C)
   \[s-\]orbitals
  done clear
  D)
   s and p-orbitals
  done clear
  View Answer play_arrow

• question_answer89) The oxidation state of Cr in chromium trioxide is
  A)
   + 3         
  done clear
  B)
   + 4
  done clear
  C)
   + 5         
  done clear
  D)
   + 6
  done clear
  View Answer play_arrow

• question_answer90) Monel metal is an alloy of
  A)
  \[Cu,Ni,Fe,Mn\]
  done clear
  B)
   \[Cu,Sn,Zn\]
  done clear
  C)
   \[Cu,Sn,P\]
  done clear
  D)
  \[Cu,Zn\]
  done clear
  View Answer play_arrow

• question_answer91) The catalyst used in the manufacture of \[{{H}_{2}}S{{O}_{4}}\]by contact process is
  A)
  \[{{V}_{2}}{{O}_{3}}\]
  done clear
  B)
  \[{{V}_{2}}{{O}_{5}}\]
  done clear
  C)
   \[FeO\]
  done clear
  D)
   \[Cu\]
  done clear
  View Answer play_arrow

• question_answer92) The tetrahedral complexes have coordination number
  A)
   3              
  done clear
  B)
   6
  done clear
  C)
   4              
  done clear
  D)
   8
  done clear
  View Answer play_arrow

• question_answer93) Potassium ferrocyanide is an example of
  A)
   tetrahedral   
  done clear
  B)
   octahedral
  done clear
  C)
   square planar
  done clear
  D)
   linear
  done clear
  View Answer play_arrow

• question_answer94) Which one amongst the following, exhibit geometrical isomerism?
  A)
  \[\text{ }\!\![\!\!\text{ C}{{\text{o}}^{\text{III}}}{{\text{(N}{{\text{H}}_{\text{3}}}\text{)}}_{\text{5}}}\text{Br }\!\!]\!\!\text{ S}{{\text{O}}_{\text{4}}}\]
  done clear
  B)
   \[C{{o}^{\text{III}}}{{[EDTA]}^{-1}}\]
  done clear
  C)
   \[{{\text{ }\!\![\!\!\text{ C}{{\text{r}}^{\text{III}}}{{(SCN)}_{6}}]}^{3-}}\]
  done clear
  D)
   \[[P{{t}^{\text{III}}}{{(N{{H}_{3}})}_{2}}C{{l}_{2}}]\]
  done clear
  View Answer play_arrow

• question_answer95) Benzoylacetonato beryllium exhibit isomerism of the type
  A)
   structural     
  done clear
  B)
   geometrical
  done clear
  C)
   optical       
  done clear
  D)
   conformational
  done clear
  View Answer play_arrow

• question_answer96) The composition of malachite is
  A)
  \[CuFe{{S}_{2}}\]
  done clear
  B)
  \[CuC{{O}_{3}}\]
  done clear
  C)
   \[CuCO3.Cu{{(OH)}_{2}}\]
  done clear
  D)
   \[Cu{{(OH)}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer97) Which one of the following metals, is extracted on smelting of its ore in blast furnace?
  A)
   Iron         
  done clear
  B)
   Sodium
  done clear
  C)
   Potassium    
  done clear
  D)
   Magnesium
  done clear
  View Answer play_arrow

• question_answer98) Prussian blue is obtained by mixing together aqueous solution of \[\text{F}{{\text{e}}^{\text{3+}}}\]salt with
  A)
   ferricyanide
  done clear
  B)
   ferrocyanide
  done clear
  C)
   hydrogen cyanide
  done clear
  D)
   sodium cyanide
  done clear
  View Answer play_arrow

• question_answer99) The reaction intermediate produced, by homolytic cleavage of a bond is called
  A)
   carbene      
  done clear
  B)
   carbocation
  done clear
  C)
   carbanion    
  done clear
  D)
   free radical
  done clear
  View Answer play_arrow

• question_answer100) The formation of cyanohydrin from a ketone is an example of
  A)
   electrophilic addition
  done clear
  B)
   nucleophilic Substitution
  done clear
  C)
   nucleophilic addition
  done clear
  D)
   electrophilic substitution
  done clear
  View Answer play_arrow

• question_answer101) According to Huckel?s rule an aromatic compound must possess
  A)
  \[(4n+1)\pi \] electrons
  done clear
  B)
  \[(4n+2)\pi \] electrons
  done clear
  C)
  \[4n\,\pi \] electrons
  done clear
  D)
  \[(4n+3)\pi \] electrons
  done clear
  View Answer play_arrow

• question_answer102) Identify the substitute group, that acts as ortho-para director, during electrophilic substitution in aromatic compounds.
  A)
   \[-N{{H}_{2}}\]
  done clear
  B)
  \[-N{{O}_{2}}\]
  done clear
  C)
   \[-S{{O}_{3}}H\]
  done clear
  D)
   \[{{N}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer103) In a group of isomeric alkyl halides, the order of boiling points is
  A)
   primary < secondary < tertiary
  done clear
  B)
   primary > secondary < tertiary
  done clear
  C)
   primary < secondary > tertiary
  done clear
  D)
   primary > secondary > tertiary
  done clear
  View Answer play_arrow

• question_answer104) On reacting with neutral ferric chloride, phenol gives
  A)
   red colour    
  done clear
  B)
   blue colour
  done clear
  C)
   violet colour  
  done clear
  D)
   green colour
  done clear
  View Answer play_arrow

• question_answer105) The hybridisation of the ipso-carbon in chlorobenzene is
  A)
   \[sp\]hybridised
  done clear
  B)
  \[~s{{p}^{2}}\] hybridised
  done clear
  C)
  \[~s{{p}^{2}}\] hybridised
  done clear
  D)
  \[~s{{p}^{3}}\] hybridised
  done clear
  View Answer play_arrow

• question_answer106) Which one of the following alcohol is used as an antifreeze reagent for making explosives?
  A)
   Glycerol      
  done clear
  B)
   Glycol
  done clear
  C)
   Ethanol      
  done clear
  D)
   Phenol
  done clear
  View Answer play_arrow

• question_answer107) \[n-\]pentane, \[iso-\]pentane, and neo-pentane are examples for isomers of the type
  A)
   geometrical  
  done clear
  B)
   optical
  done clear
  C)
   chain        
  done clear
  D)
   positional
  done clear
  View Answer play_arrow

• question_answer108) One of the following compounds exhibit geometrical isomerism
  A)
  \[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{3}}\]
  done clear
  B)
   \[C{{H}_{3}}-HC(C{{H}_{3}})-H(C)C{{H}_{3}}-C{{H}_{3}}\]
  done clear
  C)
   \[C{{H}_{3}}-HC(C{{H}_{3}})-C{{H}_{3}}\]
  done clear
  D)
   \[C{{H}_{3}}CH=CH-C{{H}_{3}}\]
  done clear
  View Answer play_arrow

• question_answer109) Different structures generated due to rotation about, C-C axis, of an organic molecule, are examples of
  A)
   geometrical isomerism
  done clear
  B)
    conformational isomerism
  done clear
  C)
   optical isomerism
  done clear
  D)
   structural isomerism
  done clear
  View Answer play_arrow

• question_answer110) The number of isomeric halopropanes produced, when propane gets halogenated, is
  A)
   1            
  done clear
  B)
   2
  done clear
  C)
   4           
  done clear
  D)
   3
  done clear
  View Answer play_arrow

• question_answer111) The acid strength obeys the order. Arrange the following carboxylic acids in the decreasing order of their reactivities
  A)
   \[C{{H}_{3}}COOH\]
  done clear
  B)
  \[ClC{{H}_{2}}COOH\]
  done clear
  C)
   \[C{{l}_{2}}CHCOOH\]
  done clear
  D)
  \[C{{l}_{3}}CCOOH\]
  done clear
  View Answer play_arrow

• question_answer112) Mohocarboxylic acids react with alcohols in the presence of an acid catalyst to form
  A)
   acid chlorides
  done clear
  B)
   acid amides
  done clear
  C)
   esters        
  done clear
  D)
   ethers
  done clear
  View Answer play_arrow

• question_answer113) On reaction with hydroxylamine, aldehydes produce
  A)
   ketoxime     
  done clear
  B)
   hydrazone
  done clear
  C)
   semicarbazone
  done clear
  D)
   aldoxime
  done clear
  View Answer play_arrow

• question_answer114) Amides are formed by the reaction of acid chloride with
  A)
  \[N{{H}_{2}}N{{H}_{2}}\]
  done clear
  B)
  \[N{{H}_{3}}\]
  done clear
  C)
   \[N{{H}_{2}}OH\]
  done clear
  D)
  \[{{C}_{6}}{{H}_{5}}NHN{{H}_{2}}\]
  done clear
  View Answer play_arrow

• question_answer115) Which one of the following, is more acidic?
  A)
   
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
   
  done clear
  View Answer play_arrow

• question_answer116) Aliphatic nitriles are prepared by the  treatment of alkyl halides with
  A)
   sodium cyanide
  done clear
  B)
   sodium isocyanide
  done clear
  C)
   sodium isocyanate                  
  done clear
  D)
   cyanamide
  done clear
  View Answer play_arrow

• question_answer117) Among the following compounds, the most basic is
  A)
   aniline       
  done clear
  B)
   acetanilide
  done clear
  C)
   \[p-\]nitroaniline
  done clear
  D)
   benzylamine
  done clear
  View Answer play_arrow

• question_answer118) Reduction of alkyl nitriles, produces
  A)
   secondary amine
  done clear
  B)
   primary amine
  done clear
  C)
   tertiary amine
  done clear
  D)
   amide
  done clear
  View Answer play_arrow

• question_answer119) Polypeptides having, molecular weights, above 10,000 are known as
  A)
   amino acids
  done clear
  B)
   harmones
  done clear
  C)
   proteins
  done clear
  D)
   terminal amino acids                
  done clear
  View Answer play_arrow

• question_answer120) Which one of the following is an example of a non-reducing sugar?
  A)
   Sucrose      
  done clear
  B)
   Lactose
  done clear
  C)
   Maltose      
  done clear
  D)
   Cellobiose
  done clear
  View Answer play_arrow

• question_answer121) The value of Rydberg constant is
  A)
  \[10,9678\,\text{c}{{\text{m}}^{-1}}\]
  done clear
  B)
  \[10,9876\,\text{c}{{\text{m}}^{-1}}\]
  done clear
  C)
   \[10,8769\,\text{c}{{\text{m}}^{-1}}\]
  done clear
  D)
   \[10,8976\,\text{c}{{\text{m}}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer122) The wavelength of a spectral line in Lyman series, when electron jumps back from 2nd orbit, is
  A)
  \[\text{1162 }\overset{\text{o}}{\mathop{\text{A}}}\,\]      
  done clear
  B)
  \[1216\overset{\text{o}}{\mathop{\text{A}}}\,\]
  done clear
  C)
   \[1362\overset{\text{o}}{\mathop{\text{A}}}\,\]
  done clear
  D)
  \[1176\overset{\text{o}}{\mathop{\text{A}}}\,\]
  done clear
  View Answer play_arrow

• question_answer123) The number of electrons accommodated in an orbit with principal quantum number 2, is
  A)
   2           
  done clear
  B)
   6
  done clear
  C)
   10          
  done clear
  D)
   8
  done clear
  View Answer play_arrow

• question_answer124) Uranium with a mass number 237 and atomic number 92, changes to a nucleus with atomic number 90 and mass number 233 on emission of
  A)
   \[\beta -\]particle     
  done clear
  B)
  \[\gamma -\]particle
  done clear
  C)
   \[\alpha -\]particle     
  done clear
  D)
   positron
  done clear
  View Answer play_arrow

• question_answer125) The only, most stable nucleus formed by bombarding, either \[_{\text{13}}\text{A}{{\text{l}}^{\text{27}}}\]by neutrons or \[_{\text{11}}\text{N}{{\text{a}}^{\text{23}}}\]by deuterons, is
  A)
  \[_{15}{{P}^{30}}\]
  done clear
  B)
  \[_{14}S{{i}^{30}}\]
  done clear
  C)
   \[_{12}M{{g}^{24}}\]
  done clear
  D)
   \[_{56}B{{a}^{137}}\]
  done clear
  View Answer play_arrow

• question_answer126) The stable  electronic configuration of chromium is
  A)
  \[3{{d}^{6}},4{{s}^{1}}\]
  done clear
  B)
  \[3{{d}^{5}},4{{s}^{2}}\]
  done clear
  C)
   \[3{{d}^{5}},4{{s}^{1}}\]
  done clear
  D)
  \[3{{d}^{6}},4{{s}^{0}}\]
  done clear
  View Answer play_arrow

• question_answer127) The half-life of \[\text{R}{{\text{a}}^{\text{226}}}\]is \[1620\text{ }yr,\] the decay constant (k) is
  A)
   0.000452    
  done clear
  B)
   0.0004278
  done clear
  C)
   0.04278      
  done clear
  D)
   0.004278
  done clear
  View Answer play_arrow

• question_answer128) According to Lowry and Bronsted, the strength of an acid depends upon
  A)
   the tendency to gain electrons
  done clear
  B)
   the tendency to loss protons
  done clear
  C)
   the tendency to accept protons
  done clear
  D)
   the tendency to loss electrons
  done clear
  View Answer play_arrow

• question_answer129) By applying law of mass action, the equilibrium constant,\[K\] for the reaction \[HA+{{H}_{2}}O\rightleftharpoons {{H}_{3}}{{O}^{+}}+\bar{A},\]is given as
  A)
  \[K=\frac{[HA][{{H}_{2}}O]}{[{{H}_{3}}{{O}^{+}}][\bar{A}]}\]
  done clear
  B)
   \[K=\frac{[{{H}_{3}}{{O}^{+}}][\bar{A}]}{[HA][{{H}_{2}}O]}\]
  done clear
  C)
   \[K=\frac{[{{H}_{3}}{{O}^{+}}][{{H}_{2}}O]}{[\bar{A}][HA]}\]
  done clear
  D)
   \[K=\frac{[HA][\bar{A}]}{[\bar{A}][HA]}\]
  done clear
  View Answer play_arrow

• question_answer130) The ionisation of strong electrolytes in acetic. acid, compared to in water, is
  A)
   weak, low
  done clear
  B)
   strong, more
  done clear
  C)
   medium, the same
  done clear
  D)
   no ionisation, 100%
  done clear
  View Answer play_arrow

• question_answer131) Calculate the pH of a solution in which hydrogen ion concentration is 0.005 g-equi/L?
  A)
   2.3           
  done clear
  B)
   2.8
  done clear
  C)
   2.9           
  done clear
  D)
   2.6
  done clear
  View Answer play_arrow

• question_answer132) Inversion of cane-sugar in dilute acid is a
  A)
   bimolecular reaction
  done clear
  B)
   Pseudo-unimolecular reaction
  done clear
  C)
   unimolecular reaction
  done clear
  D)
   trimolecular reaction
  done clear
  View Answer play_arrow

• question_answer133) The units of the rate constant of a second  order reaction are
  A)
   \[mo{{l}^{-1}}L{{\,}^{-1}}{{s}^{-1}}\]
  done clear
  B)
  \[mo{{l}^{-1}}L\,{{s}^{-1}}\]
  done clear
  C)
  \[mo{{l}^{-1}}L\,s\]
  done clear
  D)
  \[mol\,{{L}^{-1}}{{s}^{-1}}\]
  done clear
  View Answer play_arrow

• question_answer134) For the first order reaction half-life is 14 s, the time required for the initial concentration to reduce to 1/8 of its value is
  A)
  \[{{(14)}^{3}}s\]        
  done clear
  B)
   28 s
  done clear
  C)
   42 s          
  done clear
  D)
  \[{{(14)}^{2}}s\]
  done clear
  View Answer play_arrow

• question_answer135) One part of solute in one million parts of solvent is expressed as
  A)
   ppm        
  done clear
  B)
   mg/100 cc
  done clear
  C)
   g/L           
  done clear
  D)
   g/100cc
  done clear
  View Answer play_arrow

• question_answer136) The molarity of the solution obtained by dissolving 2.5 g of NaCI in 100 mL of water is
  A)
   0.00428 moles
  done clear
  B)
   428 moles
  done clear
  C)
   0.428 moles  
  done clear
  D)
   0.0428 moles
  done clear
  View Answer play_arrow

• question_answer137) The osmotic pressure is expressed in the units of
  A)
   MeV         
  done clear
  B)
   cat
  done clear
  C)
   cm/s         
  done clear
  D)
   atm
  done clear
  View Answer play_arrow

• question_answer138) Fractional distillation is a process by which the separation of different fractions from mixture of solution is carried by making use of the following property of the fractions.
  A)
   freezing point
  done clear
  B)
   boiling point.
  done clear
  C)
   melting point
  done clear
  D)
   solubility
  done clear
  View Answer play_arrow

• question_answer139) The quantity of heat measured for a reaction in a bomb calorimeter is equal to
  A)
  \[\Delta G\]
  done clear
  B)
   \[\Delta H\]
  done clear
  C)
   \[p\Delta V\]
  done clear
  D)
   \[\Delta E\]
  done clear
  View Answer play_arrow

• question_answer140)  All naturally occurring process, proceed in a direction, which leads to
  A)
   increase of enthalpy
  done clear
  B)
   increase of free energy
  done clear
  C)
   decrease of free energy
  done clear
  D)
   decrease of entropy
  done clear
  View Answer play_arrow

• question_answer141) Heat of combustion of carbon monoxide at constant volume and at \[17{{\,}^{o}}C\]is \[-67,710\,\text{cal}\text{.}\]The heat of combustion at constant pressure is
  A)
  \[~-68,000\text{ cal}\]  
  done clear
  B)
  \[~-67,800\text{ cal}\]
  done clear
  C)
  \[~-67,050\text{ cal}\]   
  done clear
  D)
  \[~+\,68,500\text{ cal}\]
  done clear
  View Answer play_arrow

• question_answer142) The free energy change \[\Delta G=0\] when
  A)
   the reactants are completely consumed
  done clear
  B)
   a catalyst is added
  done clear
  C)
   the system is at equilibrium
  done clear
  D)
   the reactants are initially mixed
  done clear
  View Answer play_arrow

• question_answer143) The units of equivalent conductance, are
  A)
   ohm \[\text{c}{{\text{m}}^{\text{2}}}\text{equivalen}{{\text{t}}^{-1}}\]
  done clear
  B)
   ohm \[\text{c}{{\text{m}}^{\text{2}}}\,\text{equivalent}\]
  done clear
  C)
  \[\text{oh}{{\text{m}}^{-1}}\,c{{m}^{2}}\,\text{equivalen}{{\text{t}}^{-1}}\]
  done clear
  D)
   \[\text{mho c}{{\text{m}}^{\text{2}}}\text{ equivalent}\]
  done clear
  View Answer play_arrow

• question_answer144) The specific conductance \[(\kappa )\] of an electrolyte of 0.1 N concentration is related to equivalent  \[(\Lambda )\]by the following formula
  A)
  \[A=\kappa \]
  done clear
  B)
  \[A=10\,\kappa \]
  done clear
  C)
   \[A=100\,\kappa \]
  done clear
  D)
  \[A=10,000\,\kappa \]
  done clear
  View Answer play_arrow

• question_answer145) The standard electrode potential of hydrogen electrode at 1 M concentration and hydrogen gas at 1 atm pressure is
  A)
  \[1\,V\]          
  done clear
  B)
  \[~6\,V\]
  done clear
  C)
  \[~8\,V\]          
  done clear
  D)
  \[~0\,V\]
  done clear
  View Answer play_arrow

• question_answer146) Pure water does not conduct electricity because it is
  A)
   basic
  done clear
  B)
   almost not ionized
  done clear
  C)
   decomposed easily
  done clear
  D)
   acidic
  done clear
  View Answer play_arrow

• question_answer147) The crystalline structure of \[\text{NaCl}\]is
  A)
   hexagonal close packing
  done clear
  B)
   face centred cubic
  done clear
  C)
   square planar
  done clear
  D)
   body centred cubic
  done clear
  View Answer play_arrow

• question_answer148) Which one, among the following, is the van der Waals' equation, describing the behaviour of one mole of a real gas over wide ranges. temperature and pressure?
  A)
  \[\left( p+\frac{a}{^{{{V}^{2}}}} \right)(V-b)=RT\]
  done clear
  B)
   \[\left( p-\frac{a}{^{{{V}^{2}}}} \right)(V-b)=RT\]
  done clear
  C)
  \[\left( p+\frac{a}{^{{{V}^{2}}}} \right)(V-b)=\frac{R}{T}\]
  done clear
  D)
   \[\left( p+\frac{a}{^{{{V}^{2}}}} \right)(V+b)=RT\]
  done clear
  View Answer play_arrow

• question_answer149) The following is a method to determine  surface tension of liquids
  A)
   single capillary method
  done clear
  B)
   refractometric method
  done clear
  C)
   polarimetric method
  done clear
  D)
   boiling point method
  done clear
  View Answer play_arrow

• question_answer150) The colloidal system of a solid dispersed in liquid medium, is called
  A)
   aerosol       
  done clear
  B)
   sol
  done clear
  C)
   gel           
  done clear
  D)
   foam
  done clear
  View Answer play_arrow

• question_answer151) If \[2\hat{i}+4\hat{j}-5\hat{k}\] and \[\hat{i}+2\hat{j}+3\hat{k}\]  are adjacent sides of a parallelogram, then the lengths of its diagonals are
  A)
   \[7,\,\sqrt{69}\]       
  done clear
  B)
   \[6,\,\sqrt{59}\]
  done clear
  C)
   \[5,\,\sqrt{65}\]
  done clear
  D)
   \[5,\,\sqrt{55}\]
  done clear
  View Answer play_arrow

• question_answer152) If the points \[\hat{i}-\hat{j}+\hat{k},\,\,\,2\hat{i}+3\hat{j}+4\hat{k}\]and  \[3\hat{i}++7\hat{j}+p\hat{k}\]are collinear, then the value of p is
  A)
   \[6\]              
  done clear
  B)
   \[5\]
  done clear
  C)
   \[4\]               
  done clear
  D)
   \[7\]
  done clear
  View Answer play_arrow

• question_answer153) If \[\hat{i}+2\hat{j}+3\hat{k}\]  and \[2\hat{i}-\hat{j}+4\hat{k}\] are the position vectors of the points A and B, then the position vector of the points of trisection of AB are
  A)
   \[\frac{4}{3}\hat{i}+\hat{j}+\frac{10}{3}\hat{k},\,\frac{5}{3}\hat{i}+\frac{11}{3}\hat{k}\]
  done clear
  B)
   \[-\frac{4}{3}\hat{i}-\hat{j}-\frac{10}{3}\hat{k},-\,\frac{5}{3}\hat{i}-\frac{11}{3}\hat{k}\]
  done clear
  C)
   \[\frac{4}{3}\hat{i}-\hat{j}-\frac{10}{3}\hat{k},-\,\frac{5}{3}\hat{i}-\frac{11}{3}\hat{k}\]
  done clear
  D)
   \[-\frac{4}{3}\hat{i}+\hat{j}-\frac{10}{3}\hat{k},\,\frac{5}{3}\hat{i}-\frac{11}{3}\hat{k}\]
  done clear
  View Answer play_arrow

• question_answer154) If \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] are three vectors such that \[|\vec{a}|=3,|\,\,\vec{b}|=4,|\,\,\vec{c}|=5\] and \[\vec{a},\,\,\vec{b},\,\,\vec{c}\] are  perpendicular    to   \[\vec{b}+\vec{c},\,\vec{c}+\vec{a},\,\,\vec{a}+\vec{b}\]respectively, then \[|\vec{a}\,+\,\vec{b}\,+\vec{c}|\] is equal to
  A)
   \[4\sqrt{2}\]         
  done clear
  B)
   \[5\sqrt{2}\]
  done clear
  C)
   \[6\sqrt{2}\]
  done clear
  D)
   \[3\sqrt{2}\]
  done clear
  View Answer play_arrow

• question_answer155) The area of a parallelogram having diagonals \[\vec{a}=3\hat{i}+\hat{j}-2\hat{k}\] and \[\vec{b}=\hat{i}-3\hat{j}+4\hat{k}\] is
  A)
   \[10\sqrt{3}\]         
  done clear
  B)
   \[5\sqrt{3}\]
  done clear
  C)
   \[8\]            
  done clear
  D)
   \[4\]
  done clear
  View Answer play_arrow

• question_answer156) If \[|\vec{a}|=10,\,\,|\vec{b}|=2\] and \[\vec{a}.\vec{b}=12,\]then \[|\vec{a}\times \vec{b}|\] is equal to
  A)
   \[12\]           
  done clear
  B)
   \[14\]
  done clear
  C)
   \[16\]           
  done clear
  D)
   \[18\]
  done clear
  View Answer play_arrow

• question_answer157) If \[\vec{a}\] and \[\vec{b}\] are unit vectors and a is the angle between them, then \[\vec{a}\,\,.\,\,\vec{b}\] will be a unit  vector, if a is equal to
  A)
   \[\frac{\pi }{4}\]           
  done clear
  B)
   \[\frac{\pi }{3}\]
  done clear
  C)
   \[\frac{2\pi }{3}\]
  done clear
  D)
   \[\frac{\pi }{2}\]
  done clear
  View Answer play_arrow

• question_answer158) The angle between the lines with direction ratios \[(4,-3,5)\] and \[(3,4,5)\] is
  A)
   \[\frac{\pi }{2}\]
  done clear
  B)
   \[\frac{\pi }{4}\]
  done clear
  C)
   \[\frac{\pi }{3}\]
  done clear
  D)
   \[\frac{\pi }{6}\]
  done clear
  View Answer play_arrow

• question_answer159) If the extremities of a diagonal of a square are \[(1,-2,3)\] and  \[(2,-3,5)\]   then the length of the side is
  A)
   \[\sqrt{6}\]       
  done clear
  B)
   \[\sqrt{3}\]
  done clear
  C)
   \[\sqrt{5}\]           
  done clear
  D)
   \[\sqrt{7}\]
  done clear
  View Answer play_arrow

• question_answer160) If the foot of the perpendicular from \[(0,0,0)\]to a plane is \[(1,2,2),\] then the equation of the plane is
  A)
   \[-x+2y+8y-9=0\]
  done clear
  B)
   \[x+2y+2z-9=0\]
  done clear
  C)
   \[x+y+z-5=0\]
  done clear
  D)
   \[x+2y-3z+1=0\]
  done clear
  View Answer play_arrow

• question_answer161) If a line makes angles \[\frac{\pi }{3}\] and \[\frac{\pi }{4}\] with the X and Y-axes respectively, then the angle made by the line and Z-axis is
  A)
   \[\frac{\pi }{2}\]
  done clear
  B)
   \[\frac{\pi }{3}\]
  done clear
  C)
   \[\frac{\pi }{4}\]
  done clear
  D)
   \[\frac{5\pi }{12}\]
  done clear
  View Answer play_arrow

• question_answer162) If \[P=(0,1,2),\,\,Q=(4,-2,1),O=(0,0,0),\] then \[\angle POQ\] is equal to
  A)
   \[\frac{\pi }{6}\]
  done clear
  B)
   \[\frac{\pi }{4}\]
  done clear
  C)
   \[\frac{\pi }{3}\]
  done clear
  D)
   \[\frac{\pi }{2}\]
  done clear
  View Answer play_arrow

• question_answer163) The direction cosines of two rays \[\overrightarrow{AB}\] and \[\overrightarrow{AC}\] are \[\left( \frac{1}{2},\frac{1}{2},-1 \right)\] and \[\left( \frac{2}{7},\frac{-3}{7},\frac{6}{7} \right).\] The direction ratios of one of the bisectors of angle \[\left( \overrightarrow{AB},\overrightarrow{AC} \right)\]are
  A)
   \[(13,\,-5,\,\,4)\]   
  done clear
  B)
   \[(13,\,5,\,\,-5)\]
  done clear
  C)
   \[(13,\,5,4)\]     
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer164) The equation of the plane passing through the points \[(a,0,0),(0,b,0)\] and \[(0,0,c)\] is
  A)
   \[ax+by+cz=0\]
  done clear
  B)
   \[ax+by+cz=1\]
  done clear
  C)
   \[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\]
  done clear
  D)
   \[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=0\]
  done clear
  View Answer play_arrow

• question_answer165) Through the point \[P(\alpha ,\,\beta ,\,\,\gamma )\] a plane is drawn at right angles to OP to meet the coordinate axes are A, B,. C respectively. If \[OP=p,\]then equation of plane \[\underset{ABC}{\longleftrightarrow}\] is
  A)
   \[\alpha x+\beta y+\gamma z=p\]
  done clear
  B)
   \[\frac{x}{\alpha }+\frac{x}{\beta }+\frac{z}{\gamma }=p\]
  done clear
  C)
   \[2\alpha x+2\beta y+2\gamma z={{p}^{2}}\]
  done clear
  D)
   \[\alpha x+\beta y+\gamma z={{p}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer166) The    solution    of    the    equation \[2{{x}^{3}}-{{x}^{2}}-22x-24=0\]when two of the roots are in the ratio \[3:4,\] is
  A)
   \[3,\,4,\frac{1}{2}\]
  done clear
  B)
   \[-\frac{3}{2},-2,4\]
  done clear
  C)
   \[-\frac{1}{2},\frac{3}{2},2\]
  done clear
  D)
   \[\frac{3}{2},2,\frac{5}{2}\]
  done clear
  View Answer play_arrow

• question_answer167) The condition that the roots of the equation \[{{x}^{3}}+3p{{x}^{2}}+3qx+r=0\] satisfied, is
  A)
   \[2{{p}^{3}}-3pq+r=0\]
  done clear
  B)
   \[2{{p}^{3}}+3pq+r=0\]
  done clear
  C)
   \[2{{p}^{3}}-3pq-r=0\]
  done clear
  D)
   \[{{p}^{3}}+3pq-r=0\]
  done clear
  View Answer play_arrow

• question_answer168) If \[\alpha ,\beta ,\gamma \] are the roots of the equation \[{{x}^{3}}-7x+7=0,\] then \[\frac{1}{{{\alpha }^{4}}}+\frac{1}{{{\beta }^{4}}}+\frac{1}{{{\gamma }^{4}}}\] is
  A)
   \[\frac{7}{3}\]
  done clear
  B)
   \[\frac{3}{7}\]
  done clear
  C)
   \[\frac{4}{7}\]
  done clear
  D)
   \[\frac{7}{4}\]
  done clear
  View Answer play_arrow

• question_answer169) At \[x=\frac{3}{2}\] the function \[f(x)=\frac{|2x-3|}{2x-3}\] is
  A)
   continuous   
  done clear
  B)
   discontinuous
  done clear
  C)
   differentiable 
  done clear
  D)
   non-zero
  done clear
  View Answer play_arrow

• question_answer170) \[\underset{x\to -1}{\mathop{\lim }}\,\frac{1+\sqrt[3]{x}}{1+\sqrt[5]{x}}\]is equal to
  A)
   \[\frac{5}{3}\]             
  done clear
  B)
   \[\frac{3}{7}\]
  done clear
  C)
   \[\frac{4}{7}\]           
  done clear
  D)
   \[\frac{-3}{5}\]
  done clear
  View Answer play_arrow

• question_answer171) \[\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{2}^{-n}}({{n}^{2}}+5n+6)}{(n+4)\,(n+5)}\] is equal to
  A)
   \[0\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[\infty \]
  done clear
  D)
   \[-\infty \]
  done clear
  View Answer play_arrow

• question_answer172) \[\underset{x\to \pi /4}{\mathop{\lim }}\,\frac{\sqrt{2}\cos \,x-1}{\cot \,x-1}\] is equal to
  A)
   \[1\]           
  done clear
  B)
   \[-\frac{1}{2}\]
  done clear
  C)
   \[\frac{1}{2\sqrt{2}}\]
  done clear
  D)
   \[\frac{1}{2}\]
  done clear
  View Answer play_arrow

• question_answer173) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{1}{x}{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)\]is equal to
  A)
   \[-2\]            
  done clear
  B)
   \[0\]
  done clear
  C)
   \[2\]               
  done clear
  D)
   \[\infty \]
  done clear
  View Answer play_arrow

• question_answer174) If n is an integer, then \[\underset{x\to n}{\mathop{\lim }}\,[x]\]
  A)
   \[n-1\]
  done clear
  B)
   \[n\]
  done clear
  C)
   does not exist
  done clear
  D)
   \[n+1\]
  done clear
  View Answer play_arrow

• question_answer175) If \[f(x)=\frac{{{e}^{1/x}}}{1+{{e}^{1/x}}}\]for \[x\ne 0\] and \[f(0)=0,\] then at \[x=0\] the function \[f(x)\] is
  A)
   continuous   
  done clear
  B)
   discontinuous
  done clear
  C)
   increasing     
  done clear
  D)
   differentiable
  done clear
  View Answer play_arrow

• question_answer176) Derivative of \[{{\log }_{10}}\,x\] with respect to \[{{x}^{2}}\]is
  A)
   \[2{{x}^{2}}\,{{\log }_{e}}\,10\]   
  done clear
  B)
   \[\frac{{{\log }_{10}}\,e}{2{{x}^{2}}}\]
  done clear
  C)
   \[\frac{{{\log }_{e}}\,10}{2{{x}^{2}}}\]     
  done clear
  D)
   \[{{x}^{2}}\,{{\log }_{e}}\,10\]
  done clear
  View Answer play_arrow

• question_answer177) The greatest value of \[si{{n}^{3}}x+co{{s}^{3}}x\]is
  A)
   \[1\]             
  done clear
  B)
   \[2\]
  done clear
  C)
   \[\sqrt{2}\]           
  done clear
  D)
   \[\sqrt{3}\]
  done clear
  View Answer play_arrow

• question_answer178) The function \[f(x)=1-{{x}^{3}}\]
  A)
   increases everywhere
  done clear
  B)
   decrease in \[(0,\infty )\]
  done clear
  C)
   increases is \[(0,\infty )\]
  done clear
  D)
   None of the above
  done clear
  View Answer play_arrow

• question_answer179) The equation of the normal line to the curve \[y=x\,{{\log }_{e}}x\] parallel to\[2x-2y+3=0\] is
  A)
   \[x+y=3{{e}^{-2}}\]  
  done clear
  B)
   \[x-y=6{{e}^{-2}}\]
  done clear
  C)
   \[x-y=3{{e}^{-2}}\]  
  done clear
  D)
   \[x-y=6{{e}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer180) If \[f(x)=\sin \,x/{{e}^{x}}\] in \[[0,\pi ],\] then \[f(x)\]
  A)
   satisfies Rollers theorem and \[c=\frac{\pi }{4},\] so  that \[f'\left( \frac{\pi }{4} \right)=4\]
  done clear
  B)
   does not satisfy Rolle's theorem but \[f'\left( \frac{\pi }{4} \right)>0\]
  done clear
  C)
   satisfies Rolle's theorem but \[f'\left( \frac{\pi }{4} \right)=0\]
  done clear
  D)
   satisfies Lagranges Mean value theorem but \[f'\left( \frac{\pi }{4} \right)\ne 0\]
  done clear
  View Answer play_arrow

• question_answer181) \[\int{\frac{1}{1+\cos \,\,ax}}\,\,dx\] is equal to
  A)
   \[\cot \,\frac{ax}{2}+c\]
  done clear
  B)
   \[\frac{1}{a}\,\tan \,\frac{ax}{2}+c\]
  done clear
  C)
   \[\frac{1}{a}(\text{cosec ax - cot ax)+c}\]
  done clear
  D)
   \[\frac{1}{a}(\text{cosec ax + cot ax)+c}\]
  done clear
  View Answer play_arrow

• question_answer182) \[\int{\frac{{{\log }_{e}}\,(\tan x)}{sin\,x\,\cos \,x}}\,\,dx\] is equal to
  A)
   \[{{[{{\log }_{e}}\,(tan\,x)]}^{2}}+c\]                      
  done clear
  B)
   \[\frac{1}{2}{{({{\log }_{e}}\,\tan x)}^{2}}+c\]                  
  done clear
  C)
   \[{{\log }_{e}}\,\,({{\log }_{e}}\,\,\tan \,x)+c\]
  done clear
  D)
   \[{{\log }_{e}}\,\,\tan \,x+c\]
  done clear
  View Answer play_arrow

• question_answer183) \[\int_{0}^{\pi }{{{\cos }^{3}}\,x\,\,dx}\]is equal to
  A)
   \[0\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[-1\]
  done clear
  D)
   \[\frac{1}{2\sqrt{2}}\]
  done clear
  View Answer play_arrow

• question_answer184) \[\int_{0}^{a}{\sqrt{{{a}^{2}}-{{x}^{2}}}}\,\,\,dx\] is equal to
  A)
   \[\pi {{a}^{2}}\]
  done clear
  B)
   \[\frac{1}{2}\pi {{a}^{2}}\]
  done clear
  C)
   \[\frac{1}{3}\pi {{a}^{2}}\]         
  done clear
  D)
   \[\frac{1}{4}\pi {{a}^{2}}\]
  done clear
  View Answer play_arrow

• question_answer185) The area bounded by the curves \[y=3x\]and \[y={{x}^{2}}\]is (in square units)
  A)
   \[10\]            
  done clear
  B)
   \[5\]
  done clear
  C)
   \[4.5\]          
  done clear
  D)
   \[9\]
  done clear
  View Answer play_arrow

• question_answer186) The order of the differential equation \[{{\left( \frac{dy}{dx} \right)}^{3}}+{{\left( \frac{dy}{dx} \right)}^{2}}+{{y}^{4}}=0\]is
  A)
   \[4\]
  done clear
  B)
   \[3\]
  done clear
  C)
   \[1\]
  done clear
  D)
   \[2\]
  done clear
  View Answer play_arrow

• question_answer187) The solution \[\frac{dy}{dx}+y={{e}^{x}}\]is
  A)
   \[2y={{e}^{2x}}+c\]
  done clear
  B)
   s\[2y{{e}^{x}}={{e}^{2}}+c\]
  done clear
  C)
   \[2y{{e}^{x}}={{e}^{2x}}+c\]
  done clear
  D)
   \[2y{{e}^{2x}}=2{{e}^{x}}+c\]
  done clear
  View Answer play_arrow

• question_answer188) When three dice are thrown the probability of getting a 4 or a 5 on each of the dice simultaneously is
  A)
   \[\frac{1}{72}\]           
  done clear
  B)
   \[\frac{1}{108}\]
  done clear
  C)
   \[\frac{1}{24}\]           
  done clear
  D)
   None of these
  done clear
  View Answer play_arrow

• question_answer189) The probability of forming a three digit number with the same digits when three digit numbers are formed out of the digits \[0,2,4,6,8\]
  A)
   \[\frac{1}{16}\]
  done clear
  B)
   \[\frac{1}{12}\]
  done clear
  C)
   \[\frac{1}{645}\]
  done clear
  D)
   \[\frac{1}{25}\]
  done clear
  View Answer play_arrow

• question_answer190) \[P(A\cup B)=\frac{1}{2},P(\bar{A})=\frac{2}{3},\] find \[P(\bar{A}\cap B)\]
  A)
   \[\frac{1}{3}\]
  done clear
  B)
   \[1\]
  done clear
  C)
   \[\frac{1}{5}\]
  done clear
  D)
   \[\frac{1}{6}\]
  done clear
  View Answer play_arrow

• question_answer191) A random variable X has the following probability distribution

  \[X(={{x}_{i}})\]	\[1\]	\[2\]	\[3\]	\[4\]
  \[P(X={{x}_{i}})\]	\[k\]	\[2k\]	\[3k\]	\[4k\]

  Then, the mean of X is
  A)
   \[3\]             
  done clear
  B)
   \[1\]
  done clear
  C)
   \[4\]            
  done clear
  D)
   \[2\]
  done clear
  View Answer play_arrow

• question_answer192) The mean and variance of a random variable X having a Binomial distribution are 4 and 2 respectively. Then, \[P(X>6)\] is equal to
  A)
   \[\frac{1}{256}\]
  done clear
  B)
   \[\frac{3}{256}\]
  done clear
  C)
   \[\frac{9}{256}\]
  done clear
  D)
   \[\frac{7}{256}\]
  done clear
  View Answer play_arrow

• question_answer193) If A and B are mutually exclusive events with \[P(A)=\frac{1}{2}\times P(B)\] and \[A\cup B=S,\] (total sample space) then \[P(A)\] is equal to
  A)
   \[\frac{2}{3}\]
  done clear
  B)
   \[\frac{1}{3}\]
  done clear
  C)
   \[\frac{1}{4}\]
  done clear
  D)
   \[\frac{3}{4}\]
  done clear
  View Answer play_arrow

• question_answer194) A coin is tossed three times. The probability of getting a head once and a tail twice is
  A)
   \[\frac{1}{8}\]
  done clear
  B)
   \[\frac{1}{3}\]
  done clear
  C)
   \[\frac{3}{8}\]
  done clear
  D)
   \[\frac{1}{2}\]
  done clear
  View Answer play_arrow

• question_answer195) The probability of choosing a number divisible by 6 or 8 from among 1 to 90 is
  A)
   \[\frac{1}{6}\]
  done clear
  B)
   \[\frac{1}{90}\]
  done clear
  C)
   \[\frac{1}{30}\]
  done clear
  D)
   \[\frac{23}{90}\]
  done clear
  View Answer play_arrow

• question_answer196) If the function \[f:R\to R\] denned by \[f(x)=[x]\]where \[[x]\] is the greatest integer not exceeding x, for \[x\in R\] then /is
  A)
   even
  done clear
  B)
   odd
  done clear
  C)
   neither even nor odd
  done clear
  D)
   strictly increasing
  done clear
  View Answer play_arrow

• question_answer197) If \[f:R\to R\] is given by \[f(x)=\left\{ \begin{matrix}    -1,\,when\,\,x\,\,is\,\,rational  \\    1,\,when\,\,x\,\,is\,\,irrational  \\ \end{matrix} \right.\] then \[(fof)\,(1-\sqrt{3})\] is equal to
  A)
   \[1\]             
  done clear
  B)
   \[-1\]
  done clear
  C)
   \[\sqrt{3}\]           
  done clear
  D)
   \[0\]
  done clear
  View Answer play_arrow

• question_answer198) If \[\frac{{{(1+i)}^{2}}}{2-i}=x+iy,\] then \[x+y\] is equal to
  A)
   \[-\frac{2}{5}\]
  done clear
  B)
   \[\frac{6}{5}\]
  done clear
  C)
   \[\frac{2}{5}\]
  done clear
  D)
   \[-\frac{6}{5}\]
  done clear
  View Answer play_arrow

• question_answer199) If \[1,\,\omega ,\,{{\omega }^{2}}\] are the cube roots of unity, then \[(1-\omega +{{\omega }^{2}})(1-{{\omega }^{2}}+{{\omega }^{4}})(1-{{\omega }^{4}}+{{\omega }^{8}})\] \[(1-{{\omega }^{8}}+{{\omega }^{16}})....\] upto 2n factors is
  A)
   \[2n\]              
  done clear
  B)
   \[{{2}^{2n}}\]
  done clear
  C)
   \[1\]              
  done clear
  D)
   \[-{{2}^{2n}}\]
  done clear
  View Answer play_arrow

• question_answer200) If \[\alpha \] and \[\beta \] are the roots of \[{{x}^{2}}+5x+4=0,\]then equation whose roots are \[\frac{\alpha +2}{3},\frac{\beta +2}{3}\]is
  A)
   \[9{{x}^{2}}+3x+2=0\]
  done clear
  B)
   \[9{{x}^{2}}-3x-2=0\]
  done clear
  C)
   \[9{{x}^{2}}+3x-2=0\]
  done clear
  D)
   \[9{{x}^{2}}-3x+2=0\]
  done clear
  View Answer play_arrow

• question_answer201) If the difference between the roots of \[{{x}^{2}}+ax-b=0\]is equal to the difference between the roots of \[{{x}^{2}}-px+q=0,\]then \[{{a}^{2}}-{{p}^{2}}\]in terms of b and q is
  A)
   \[-4(b+q)\]     
  done clear
  B)
    \[4(b+q)\]
  done clear
  C)
   \[4(b-q)\]       
  done clear
  D)
   \[4(q-b)\]
  done clear
  View Answer play_arrow

• question_answer202) In a geometric progression (GP) the ratio of the sum of the 1st three terms and first six terms is \[125:152\] the common ratio is
  A)
   \[\frac{1}{5}\]              
  done clear
  B)
   \[\frac{2}{5}\]
  done clear
  C)
   \[\frac{4}{5}\]             
  done clear
  D)
   \[\frac{3}{5}\]
  done clear
  View Answer play_arrow

• question_answer203) The term independent of x in the expansion of \[\left( \frac{2\sqrt{x}}{x}-\frac{1}{2x\sqrt{x}} \right)\] is
  A)
   5th term     
  done clear
  B)
   6th term
  done clear
  C)
   11 th term    
  done clear
  D)
   no term
  done clear
  View Answer play_arrow

• question_answer204) The mid points of the sides of a triangle are \[D(6,1),\,\,E(3,\,5)\] and \[F(-1,-2),\] then the vertex opposite to D is
  A)
   \[(-4,2)\]       
  done clear
  B)
    \[(-4,5)\]
  done clear
  C)
   \[(2,\,5)\]         
  done clear
  D)
   \[(10,\,8)\]
  done clear
  View Answer play_arrow

• question_answer205) If the centroid of the triangle formed by the points \[(0,\,0),\,\,(\cos \theta ,\sin \theta )\] and \[(sin\theta ,-\cos \theta )\] lies on the line \[y=2x,\]then \[\theta \] is equal to
  A)
   \[{{\tan }^{-1}}\,\,2\]       
  done clear
  B)
   \[{{\tan }^{-1}}\,\,3\]
  done clear
  C)
   \[{{\tan }^{-1}}\,\,(-3)\]   
  done clear
  D)
   \[{{\tan }^{-1}}\,\,(-2)\]
  done clear
  View Answer play_arrow

• question_answer206) The point of concurrence of the lines \[ax+by+c=0\]and \[a,b,c\]satisfy the relation \[3a+2b+4c=0\]is
  A)
   \[\left( \frac{3}{2},\frac{1}{4} \right)\]
  done clear
  B)
   \[\left( \frac{3}{4},\frac{1}{4} \right)\]
  done clear
  C)
   \[\left( \frac{3}{4},\frac{1}{2} \right)\]
  done clear
  D)
   \[\left( \frac{3}{2},\frac{1}{2} \right)\]
  done clear
  View Answer play_arrow

• question_answer207) If 3, 4 are intercepts of a line \[L=0,\]then the distance of \[L=0\]from the origin is
  A)
   5 unit        
  done clear
  B)
   12 unit
  done clear
  C)
   \[\frac{5}{12}\]unit       
  done clear
  D)
   \[\frac{12}{5}\]unit
  done clear
  View Answer play_arrow

• question_answer208) The angle between the pair of lines \[({{x}^{2}}+{{y}^{2}}){{\sin }^{2}}\alpha ={{(x\,\cos \theta -y\,\sin \theta )}^{2}}\] is
  A)
   \[\theta \]
  done clear
  B)
   \[2\,\theta \]
  done clear
  C)
   \[\alpha \]
  done clear
  D)
   \[2\,\alpha \]
  done clear
  View Answer play_arrow

• question_answer209) The other end of the diameter through the point \[(-1,1)\]     on     the     circle \[{{x}^{2}}+{{y}^{2}}-6x+4y-12=0\]'              
  A)
   \[(-7,5)\]       
  done clear
  B)
   \[(-7,-5)\]
  done clear
  C)
   \[(7,-5)\]
  done clear
  D)
   \[(7,5)\]
  done clear
  View Answer play_arrow

• question_answer210) In the parabola \[{{y}^{2}}=4ax,\]the length of the  chord passing through the vertex inclined to the axis at\[\frac{\pi }{4}\] is                   
  A)
   \[4a\sqrt{2}\]
  done clear
  B)
   \[2a\sqrt{2}\]
  done clear
  C)
   \[a\sqrt{2}\]
  done clear
  D)
   \[a\]
  done clear
  View Answer play_arrow

• question_answer211) If \[\frac{1+\cos A}{1-\cos A}=\frac{{{m}^{2}}}{{{n}^{2}}},\] then tan A is equal to
  A)
   \[\pm \frac{2mn}{{{m}^{2}}+{{n}^{2}}}\]
  done clear
  B)
   \[\pm \frac{2mn}{{{m}^{2}}-{{n}^{2}}}\]
  done clear
  C)
   \[\frac{{{m}^{2}}+{{n}^{2}}}{{{m}^{2}}-{{n}^{2}}}\]
  done clear
  D)
   \[\frac{{{m}^{2}}-{{n}^{2}}}{{{m}^{2}}+{{n}^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer212) If \[\alpha +\beta =\frac{\pi }{4},\]then the value of \[(1+\tan \alpha )\] \[(1+\tan \beta )\]is equal to                      
  A)
   \[1\]             
  done clear
  B)
   \[-1\]
  done clear
  C)
   \[2\]             
  done clear
  D)
   \[-2\]                
  done clear
  View Answer play_arrow

• question_answer213) The value of \[{{\cos }^{2}}\left( \frac{\pi }{4}+\theta  \right)-{{\sin }^{2}}\left( \frac{\pi }{4}-\theta  \right)\]is   
  A)
   \[0\]
  done clear
  B)
   \[\cos \,\,2\theta \]
  done clear
  C)
   \[sin\,\,2\theta \]
  done clear
  D)
   \[\cos \,\theta \]
  done clear
  View Answer play_arrow

• question_answer214) The solutions of \[x+\sin \,5x=\sin 3x\] in \[\left( 0,\frac{\pi }{2} \right)\]
  A)
   \[\frac{\pi }{4},\frac{\pi }{10}\]
  done clear
  B)
   \[\frac{\pi }{6},\frac{\pi }{3}\]
  done clear
  C)
   \[\frac{\pi }{4},\frac{\pi }{2}\]
  done clear
  D)
   \[\frac{\pi }{8},\frac{\pi }{16}\]
  done clear
  View Answer play_arrow

• question_answer215) If \[\cot \,x+\,\text{cosec x = }\sqrt{3},\] the principal value of \[\left( x-\frac{\pi }{6} \right)\]is
  A)
   \[\frac{\pi }{3}\]
  done clear
  B)
   \[\frac{\pi }{4}\]
  done clear
  C)
   \[\frac{\pi }{2}\]
  done clear
  D)
   \[\frac{\pi }{6}\]
  done clear
  View Answer play_arrow

• question_answer216) The value of \[{{\cos }^{-1}}\left( -\frac{1}{2} \right)\] among the following, is
  A)
   \[\frac{9\pi }{3}\]
  done clear
  B)
   \[\frac{8\pi }{3}\]
  done clear
  C)
   \[\frac{5\pi }{3}\]
  done clear
  D)
   \[\frac{11\pi }{3}\]
  done clear
  View Answer play_arrow

• question_answer217) The value of \[{{\cot }^{-1}}\,9+\text{cose}{{\text{c}}^{-1}}\frac{\sqrt{41}}{4}\]is
  A)
   \[\frac{\pi }{2}\]
  done clear
  B)
   \[\frac{\pi }{4}\]
  done clear
  C)
   \[\frac{\pi }{3}\]
  done clear
  D)
   \[\pi \]
  done clear
  View Answer play_arrow

• question_answer218) If \[\left| \begin{matrix}    1 & 1 & 0  \\    2 & 0 & 3  \\    5 & -6 & x  \\ \end{matrix} \right|=29,\] then x is
  A)
   \[1\]
  done clear
  B)
   \[2\]
  done clear
  C)
    \[3\]
  done clear
  D)
   \[4\]
  done clear
  View Answer play_arrow

• question_answer219) If \[A=\left[ \begin{matrix}    0 & 1 & 0  \\    1 & 0 & 0  \\    0 & 0 & 1  \\ \end{matrix} \right],\] then \[{{A}^{-1}}\]is equal to
  A)
   \[2A\]
  done clear
  B)
   \[A\]
  done clear
  C)
   \[-A\]
  done clear
  D)
   \[I\]
  done clear
  View Answer play_arrow

• question_answer220) If \[x\left[ \begin{matrix}    -3  \\    4  \\ \end{matrix} \right]+y\left[ \begin{matrix}    4  \\    3  \\ \end{matrix} \right]=\left[ \begin{matrix}    10  \\    -5  \\ \end{matrix} \right],\] then
  A)
   \[x=-2,\,y=1\]
  done clear
  B)
   \[x=-9,y=10\]
  done clear
  C)
   \[x=22,y=1\]
  done clear
  D)
   \[x=2,y=-1\]
  done clear
  View Answer play_arrow

• question_answer221) Let A be a square matrix and \[{{A}^{T}}\] is its transpose, then \[A+{{A}^{T}}\]is
  A)
   a diagonal matrix
  done clear
  B)
   a symmetric matrix
  done clear
  C)
   the identity matrix
  done clear
  D)
   a skew-symmetric matrix
  done clear
  View Answer play_arrow

• question_answer222) If \[\left| \begin{matrix}    x & y & z  \\    -x & y & z  \\    x & -y & z  \\ \end{matrix} \right|=kxyz,\] then k is equal to
  A)
   \[1\]
  done clear
  B)
   \[3\]
  done clear
  C)
   \[4\]
  done clear
  D)
   \[2\]
  done clear
  View Answer play_arrow

• question_answer223) The system of equations \[3x-y+4z=3\] \[x+2y-3z=-2\] \[6x+5y+\lambda z=-3\] has at least one solution, if
  A)
   \[\lambda =-5\]       
  done clear
  B)
   \[\lambda =5\]
  done clear
  C)
   \[\lambda =3\]
  done clear
  D)
   \[\lambda =-13\]
  done clear
  View Answer play_arrow

• question_answer224) The inverse of   \[\left[ \begin{matrix}    5 & 2  \\    3 & 1  \\ \end{matrix} \right]\]is
  A)
   \[\left[ \begin{matrix}    1 & -2  \\    -3 & 5  \\ \end{matrix} \right]\]
  done clear
  B)
   \[\left[ \begin{matrix}    -1 & 2  \\    3 & -5  \\ \end{matrix} \right]\]
  done clear
  C)
   \[\left[ \begin{matrix}    -1 & -2  \\    -3 & -5  \\ \end{matrix} \right]\]
  done clear
  D)
   \[\left[ \begin{matrix}    1 & 2  \\    3 & 5  \\ \end{matrix} \right]\]
  done clear
  View Answer play_arrow

• question_answer225) \[A=\left[ \begin{matrix}    \cos \alpha  & -\sin \alpha  & 0  \\    \sin \alpha  & \cos \alpha  & 0  \\    0 & 0 & 1  \\ \end{matrix} \right],\] then \[{{A}^{-1}}\] is
  A)
   \[A\]
  done clear
  B)
   \[-A\]
  done clear
  C)
   \[adj\,(A)\]
  done clear
  D)
   \[-adj\,(A)\]
  done clear
  View Answer play_arrow