-
question_answer1)
If an event cannot occur, then its probability is: (NCERT EXEMPLAR)
A)
\[1\] done
clear
B)
\[\frac{3}{4}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[0\] done
clear
View Solution play_arrow
-
question_answer2)
Which of the following cannot be the probability of an event? (NCERT EXEMPLAR)
A)
\[\frac{1}{3}\] done
clear
B)
\[0.1\] done
clear
C)
\[3%\] done
clear
D)
\[\frac{17}{16}\] done
clear
View Solution play_arrow
-
question_answer3)
An event is very unlikely to happen. Its probability is Closest to: (NCERT EXEMPLAR)
A)
\[0.0001\] done
clear
B)
\[0.001\] done
clear
C)
\[0.01\] done
clear
D)
\[0.1\] done
clear
View Solution play_arrow
-
question_answer4)
If the probability of an event is p, the probability of its complementary event will be: (NCERT EXEMPLAR)
A)
\[p-1\] done
clear
B)
\[p\] done
clear
C)
\[1-p\] done
clear
D)
\[1-\frac{1}{p}\] done
clear
View Solution play_arrow
-
question_answer5)
The probability expressed as a percentage of a particular occurrence can never be: (NCERT EXEMPLAR)
A)
less than 100 done
clear
B)
less than 0 done
clear
C)
greater than 1 done
clear
D)
anything but a whole number done
clear
View Solution play_arrow
-
question_answer6)
Which of the following can be the probability of an event: (NCERT EXEMPLAR)
A)
\[-0.04\] done
clear
B)
\[1.004\] done
clear
C)
\[\frac{18}{23}\] done
clear
D)
\[\frac{8}{7}\] done
clear
View Solution play_arrow
-
question_answer7)
Which of the following cannot be the probability of an event? (NCERT EXEMPLAR)
A)
\[\frac{2}{3}\] done
clear
B)
\[-15\] done
clear
C)
\[15%\] done
clear
D)
\[0.7\] done
clear
View Solution play_arrow
-
question_answer8)
Probability of an event cannot be:
A)
0 done
clear
B)
1 done
clear
C)
negative done
clear
D)
positive done
clear
View Solution play_arrow
-
question_answer9)
A fair dice is rolled. Probability of getting a number x such that \[1\le x\le 6,\] is:
A)
0 done
clear
B)
\[>1\] done
clear
C)
between 0 and 1 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer10)
The sum of the probabilities of all elementary events of an experiment is p, then:
A)
\[0<p<1\] done
clear
B)
\[0\le p<1\] done
clear
C)
\[p=1\] done
clear
D)
\[p=0\] done
clear
View Solution play_arrow
-
question_answer11)
For an event E, \[P(E)+P(\bar{E})=q,\]then:
A)
\[0\le q<1\] done
clear
B)
\[0<q\le 1\] done
clear
C)
\[0<q<1\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer12)
A fair dice is rolled. The probability of getting a number; more than six is:
A)
\[1<0\] done
clear
B)
\[\ge 1\] done
clear
C)
\[0\] done
clear
D)
cannot be determined done
clear
View Solution play_arrow
-
question_answer13)
The probability of a sure event is:
A)
\[0\] done
clear
B)
\[1\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
greater than 0 and less than 1, done
clear
View Solution play_arrow
-
question_answer14)
The probability of an impossible event is:
A)
\[0\] done
clear
B)
\[1\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
a number laying between 0 and 1. done
clear
View Solution play_arrow
-
question_answer15)
If p is the probability of the occurrence of an event, then the probability of non-occurrence of that event is:
A)
\[1-p\] done
clear
B)
\[p\] done
clear
C)
\[2p\] done
clear
D)
\[\frac{1}{2}p\] done
clear
View Solution play_arrow
-
question_answer16)
If the probability of the non-happening of an event is q, then the probability of happening of that event is:
A)
\[1-q\] done
clear
B)
\[q\] done
clear
C)
\[\frac{q}{2}\] done
clear
D)
\[2q\] done
clear
View Solution play_arrow
-
question_answer17)
If p is the probability of happening of an event and q is the probability of non-happening of the event, then \[p+q\] is equal to:
A)
0 done
clear
B)
1 done
clear
C)
\[-1\] done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer18)
Which of the following is true?
A)
\[0\le P(E)\le 1\] done
clear
B)
\[P(E)>1\] done
clear
C)
\[P(E)<0\] done
clear
D)
\[-\frac{1}{2}\le P(E)\le \frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer19)
The sum of the probabilities of all the elementary events of an experiment is:
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer20)
Which of the following cannot be the probability of an event?
A)
1 done
clear
B)
\[20%\] done
clear
C)
\[0.3\] done
clear
D)
\[\frac{5}{2}\] done
clear
View Solution play_arrow
-
question_answer21)
Which of the following relationship is the correct?
A)
\[P(E)+P(\bar{E})=1\] done
clear
B)
\[P(\bar{E})-P(E)=1\] done
clear
C)
\[P(E)=1+P(\bar{E})\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer22)
If probability of success is \[0.\text{9}%,\] then probability of failure is:
A)
\[0.\text{91}\] done
clear
B)
\[0.0\text{91}\] done
clear
C)
99.1 done
clear
D)
\[0.\text{991}\] done
clear
View Solution play_arrow
-
question_answer23)
The probability of passing a certain test is \[\frac{x}{24}\]. If the probability of not passing it is \[\frac{7}{8},\] then x is equal to:
A)
2 done
clear
B)
3 done
clear
C)
4 done
clear
D)
6 done
clear
View Solution play_arrow
-
question_answer24)
A girl calculates that the probability of her winning the first prize in a Lottery is\[0.0\text{8}\]. If 6000 tickets are sold, how many tickets has she bought? (NCERT EXEMPLAR)
A)
40 done
clear
B)
240 done
clear
C)
480 done
clear
D)
750 done
clear
View Solution play_arrow
-
question_answer25)
The probability of selecting a rotten apple randomly from a heap of 900 apples is \[0.\text{18}\]. What is the number of rotten apples in the heap? (CBSE 2017)
A)
152 done
clear
B)
155 done
clear
C)
162 done
clear
D)
173 done
clear
View Solution play_arrow
-
question_answer26)
The probability of guessing the correct answer to certain question is\[\text{P}/\text{12}\]. If the probability of not guessing the correct answer to same question is \[3/4,\] then the value of P is:
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer27)
The probability that it will rain tomorrow is\[0.\text{3}\]. What is the probability that it will not rain tomorrow?
A)
\[0.\text{3}\] done
clear
B)
\[0.2\] done
clear
C)
\[0.7\] done
clear
D)
\[0.07\] done
clear
View Solution play_arrow
-
question_answer28)
A single letter is selected at random from the word 'PROBABILITY'. The probability that it is a vowel is:
A)
\[\frac{3}{11}\] done
clear
B)
\[\frac{4}{11}\] done
clear
C)
\[\frac{2}{11}\] done
clear
D)
\[\frac{5}{11}\] done
clear
View Solution play_arrow
-
question_answer29)
Two coins are tossed simultaneously. The probability of getting no head is:
A)
\[\frac{1}{4}\] done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[1\] done
clear
View Solution play_arrow
-
question_answer30)
In tossing a die, the probability of getting a number 8 is:
A)
\[0\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer31)
The probability of getting any day in a week is:
A)
\[\frac{1}{7}\] done
clear
B)
\[\frac{2}{7}\] done
clear
C)
\[1\] done
clear
D)
\[0\] done
clear
View Solution play_arrow
-
question_answer32)
A die is thrown once. What is the probability of getting 4 on it?
A)
\[\frac{1}{4}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer33)
A card is drawn at random from a well shuffled deck of 52 playing cards. What is the probability of getting a black king? (CBSE 2020)
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{1}{26}\] done
clear
C)
\[\frac{3}{13}\] done
clear
D)
\[\frac{9}{13}\] done
clear
View Solution play_arrow
-
question_answer34)
A card is drawn at random from a well-shuffled pack of 52 cards, the probability of getting a red king is: (CBSE 2020)
A)
\[\frac{1}{26}\] done
clear
B)
\[\frac{1}{13}\] done
clear
C)
\[\frac{2}{13}\] done
clear
D)
\[\frac{7}{13}\] done
clear
View Solution play_arrow
-
question_answer35)
What is the probability of getting a tail on throwing an unbiased coin?
A)
1 done
clear
B)
0 done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer36)
What is the probability of getting a head on throwing an unbiased coin?
A)
0 done
clear
B)
1 done
clear
C)
\[-1\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer37)
The probability of getting a number greater than 2 is throwing a die is:
A)
\[2/3\] done
clear
B)
\[1/3\] done
clear
C)
\[4/3\] done
clear
D)
\[1/4\] done
clear
View Solution play_arrow
-
question_answer38)
A fair die is thrown once. The probability for getting a composite number less than 5 is:
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer39)
A letter is chosen at random from the English alphabets. Find the probability that the Letter chosen succeeds V.
A)
\[\frac{2}{13}\] done
clear
B)
\[\frac{5}{26}\] done
clear
C)
\[\frac{1}{26}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer40)
In a single throw of a die, the probability of getting a multiple of 2 is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer41)
In tossing a die, the probability of getting an even number or a number less than 4 is:
A)
1 done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
\[\frac{5}{6}\] done
clear
View Solution play_arrow
-
question_answer42)
If a die is thrown, what is the probability of getting a number less than 4 and greater than 3?
A)
0 done
clear
B)
1 done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer43)
A die is thrown once. The probability of getting a prime number is: (CBSE2020)
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{6}\] done
clear
View Solution play_arrow
-
question_answer44)
A card is selected from a deck of 52 cards. The probability of its being a red face card is: (NCERT EXEMPLAR)
A)
\[\frac{3}{26}\] done
clear
B)
\[\frac{3}{13}\] done
clear
C)
\[\frac{2}{13}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer45)
When a die is thrown, the probability of getting an odd number less than 3 is: (NCERT EXEMPLAR)
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer46)
A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is: (NCERT EXEMPLAR)
A)
4 done
clear
B)
13 done
clear
C)
48 done
clear
D)
51 done
clear
View Solution play_arrow
-
question_answer47)
The probability of getting a bad egg in a lot of 400 is\[0.0\text{35}\]. The number of bad eggs in the lot is: (NCERT EXEMPIAR)
A)
7 done
clear
B)
14 done
clear
C)
21 done
clear
D)
28 done
clear
View Solution play_arrow
-
question_answer48)
Probability of getting an even number of throwing a die is:
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{5}{6}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer49)
If a die is thrown once, the probability of getting a number less than 3 and greater than 2 is:
A)
1 done
clear
B)
0 done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer50)
In a throw of a die, the probability of getting an odd ' number less than 6 is: (CBSE 2013)
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer51)
The probability of throwing a number greater than 2 with a fair die is:
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{5}{6}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{2}{5}\] done
clear
View Solution play_arrow
-
question_answer52)
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.
A)
\[\frac{1}{26}\] done
clear
B)
\[\frac{1}{13}\] done
clear
C)
\[\frac{1}{52}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer53)
A bag contains 4 red and 6 black balls. A ball is taken out of the bag at random. Find the probability of getting a black ball.
A)
\[\frac{2}{5}\] done
clear
B)
\[\frac{3}{5}\] done
clear
C)
\[\frac{4}{5}\] done
clear
D)
\[\frac{1}{5}\] done
clear
View Solution play_arrow
-
question_answer54)
A bag contains 4 red, 5 black and 3 yellow balls. A ball taken out of the bag at random. Find the probability than the ball taken out is of yellow colour.
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
\[\frac{1}{5}\] done
clear
View Solution play_arrow
-
question_answer55)
A die is thrown once. Find the probability of getting number greater than 5.
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer56)
A dice is thrown once. Find the probability of getting number less than 5.
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer57)
A card is drawn from a well-shuffled pack of 52 cards. What is the probability that it is an ace of spade?
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{1}{26}\] done
clear
C)
\[\frac{1}{39}\] done
clear
D)
\[\frac{1}{52}\] done
clear
View Solution play_arrow
-
question_answer58)
In one thousand lottery tickets, there are 50 prizes to be given. Find the probability to Manish winning a prize, who bought one ticket.
A)
\[\frac{1}{10}\] done
clear
B)
\[\frac{1}{100}\] done
clear
C)
\[\frac{1}{1000}\] done
clear
D)
\[\frac{1}{20}\] done
clear
View Solution play_arrow
-
question_answer59)
Out of one digit prime numbers, one number is selected random. The probability of selecting an even number is
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{4}{9}\] done
clear
D)
\[\frac{2}{5}\] done
clear
View Solution play_arrow
-
question_answer60)
If in a lottery, there are 5 prizes and 20 blanks, then the probability of getting a prize is:
A)
\[\frac{2}{5}\] done
clear
B)
\[\frac{4}{5}\] done
clear
C)
\[\frac{1}{5}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer61)
Two dice are thrown together. The probability that sum the two numbers will be a multiple of 4, is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{8}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer62)
A bag contains 4 red, 5 black and 3 yellow balls. A ball is taken out of the bag at random. Find the probability that the ball taken out is not of red colour.
A)
1 done
clear
B)
4 done
clear
C)
5 done
clear
D)
25 done
clear
View Solution play_arrow
-
question_answer63)
| A child has a block is the shape of a cube with one letter written on each face as follows: |
 |
| The cube is thrown once. What is the probability of getting A? |
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer64)
A letter is chosen at random from the English alphabet. Find the probability that the letter chosen succeeds X.
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{1}{52}\] done
clear
C)
\[\frac{1}{26}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer65)
A card is drawn from a well shuffled deck of playing cards. Find the probability of drawing a black face card.
A)
\[\frac{1}{26}\] done
clear
B)
\[\frac{3}{26}\] done
clear
C)
\[\frac{1}{52}\] done
clear
D)
\[\frac{3}{52}\] done
clear
View Solution play_arrow
-
question_answer66)
Cards maked with number \[2,\,4,\,6,\,8,\,10\,........,\,50\] are placed in a bag and mixed thoroughly. One cards is then drawn. What is the probability that the card is marked with a prime number?
A)
\[\frac{1}{25}\] done
clear
B)
\[\frac{1}{50}\] done
clear
C)
\[\frac{1}{100}\] done
clear
D)
\[\frac{1}{10}\] done
clear
View Solution play_arrow
-
question_answer67)
A bag contains 4 red, 5 black and 3 yellow balls. A ball is taken out of the bag random. Find the probability that the ball taken out is not of red colour.
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer68)
Two coins are tossed simultaneously. The probability of getting a head on only or of the two coins is:
A)
1 done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
\[\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer69)
| A child has a die whose six faces show the number as given below: |
 |
| The die is thrown once. What is the probability of getting 5? |
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
0 done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer70)
Among 52 cards, there are 12 face cards. Probability that a card drawn at random is not a face card is:
A)
\[\frac{3}{13}\] done
clear
B)
\[\frac{9}{13}\] done
clear
C)
\[\frac{10}{13}\] done
clear
D)
\[\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer71)
The probability that a leap year should have exactly 52 Tuesday is:
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{3}{7}\] done
clear
C)
1 done
clear
D)
\[\frac{5}{7}\] done
clear
View Solution play_arrow
-
question_answer72)
A card is drawn from a pack of cards numbered 2 to 53. The probability that the number on the card is a prime number Less than 20 is:
A)
\[\frac{2}{13}\] done
clear
B)
\[\frac{4}{13}\] done
clear
C)
\[\frac{5}{13}\] done
clear
D)
\[\frac{8}{13}\] done
clear
View Solution play_arrow
-
question_answer73)
The probability of getting a number between 1 and 100 which is divisible by 1 and itself only is:
A)
\[\frac{29}{98}\] done
clear
B)
\[\frac{1}{2}\] done
clear
C)
\[\frac{25}{98}\] done
clear
D)
\[\frac{23}{98}\] done
clear
View Solution play_arrow
-
question_answer74)
Two unbiased dice are thrown. The probability that the total score is more than 5 is:
A)
\[\frac{1}{18}\] done
clear
B)
\[\frac{5}{18}\] done
clear
C)
\[\frac{7}{18}\] done
clear
D)
\[\frac{13}{18}\] done
clear
View Solution play_arrow
-
question_answer75)
A coin is tossed twice. The probability of getting both head is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer76)
The probability of a non-leap year having 53 Monday is
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{1}{7}\] done
clear
C)
\[\frac{5}{7}\] done
clear
D)
\[\frac{6}{7}\] done
clear
View Solution play_arrow
-
question_answer77)
A card is drawn from a well-shuffled deck of 52 playing cards. The probability that the card will not be an ace is:
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{12}{13}\] done
clear
D)
\[\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer78)
Cards bearing numbers \[\text{2},\text{ 5},\text{4},...,\text{ 11}\]are kept in a bag. A card is drawn at random from the bag. The probability of getting a card with a prime number is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{3}{10}\] done
clear
D)
\[\frac{5}{9}\] done
clear
View Solution play_arrow
-
question_answer79)
What is the probability that a randomly taken Leap year has 52 Sunday?
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{3}{7}\] done
clear
C)
\[\frac{5}{7}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer80)
A box contains 90 discs, numbered from 1 to 9. If one disc is drawn at random from the box, the probability that it bears a prime number less than 23 is: (CBSE 2013)
A)
\[\frac{4}{15}\] done
clear
B)
\[\frac{7}{90}\] done
clear
C)
\[\frac{4}{45}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer81)
A box contains cards numbered 6 to 50. A card is drawn at random from the box, the probability that the drawn card has a number which is a perfect square is: (CBSE 2013, 16)
A)
\[\frac{1}{9}\] done
clear
B)
\[\frac{2}{3}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{7}{18}\] done
clear
View Solution play_arrow
-
question_answer82)
Two different dice are tossed together. The probability that the product of the two numbers on the top of the dice is 6, is: (CBSE 2015)
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{9}\] done
clear
D)
\[\frac{7}{36}\] done
clear
View Solution play_arrow
-
question_answer83)
Two coins are tossed simultaneously. The probability of getting exactly one head is: (CBSE 2013)
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer84)
If two different dice are rolled together, the probability of getting an even number on both dice is: (CBSE2014, 15)
A)
\[\frac{1}{4}\] done
clear
B)
\[\frac{5}{18}\] done
clear
C)
\[\frac{7}{36}\] done
clear
D)
\[\frac{1}{6}\] done
clear
View Solution play_arrow
-
question_answer85)
Probability of getting exactly two heads on the tossing of two coins simultaneously is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer86)
If two dice are thrown once, then the probability of getting a total of 10 is:
A)
\[\frac{5}{12}\] done
clear
B)
\[\frac{7}{12}\] done
clear
C)
\[\frac{1}{12}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer87)
If two dice are thrown once, then the probability of getting a total more than 9 is:
A)
\[\frac{5}{6}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer88)
The probability of getting an even number or a multiple of 3 if an unbiased die is thrown, is:
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer89)
A bag contains 3 red balls, 5 white balls and 7 black balls. What is the probability that a ball drawn from the bag at random will be neither red nor black? (NCERT EXEMPLAR)
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{7}{15}\] done
clear
D)
\[\frac{8}{15}\] done
clear
View Solution play_arrow
-
question_answer90)
One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number, which is a multiple of 5 is: (NCERT EXEMPLAR)
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{3}{5}\] done
clear
C)
\[\frac{4}{5}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer91)
Someone is asked to take a number from 1 to 100. The probability that it is a prime is: (NCERT EXEMPLAR)
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{6}{25}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
\[\frac{13}{50}\] done
clear
View Solution play_arrow
-
question_answer92)
An integer is chosen between 0 to 50. What is the probability that it is divisible by 4?
A)
\[\frac{12}{49}\] done
clear
B)
\[\frac{13}{49}\] done
clear
C)
\[\frac{1}{7}\] done
clear
D)
\[\frac{4}{49}\] done
clear
View Solution play_arrow
-
question_answer93)
A coin is tossed twice. The probability of getting both tails is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{4}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer94)
A die is thrown once. Find the probability of getting an odd prime number.
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{6}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer95)
A card is drawn at random from a pack of 52 cards. The probability that the drawn card is not a king is:
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{9}{13}\] done
clear
C)
\[\frac{4}{13}\] done
clear
D)
\[\frac{12}{13}\] done
clear
View Solution play_arrow
-
question_answer96)
From a well shuffled pack of 52 cards, a card is drawn at random. The probability of getting a red king is:
A)
\[\frac{1}{13}\] done
clear
B)
\[\frac{1}{26}\] done
clear
C)
\[\frac{1}{52}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer97)
A month is selected at random from a year. The probability that it is May or July is:
A)
\[\frac{1}{12}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{1}{3}\] done
clear
View Solution play_arrow
-
question_answer98)
Two dice are rolled simultaneously. The probability that they show different faces is:
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{1}{3}\] done
clear
D)
\[\frac{5}{6}\] done
clear
View Solution play_arrow
-
question_answer99)
A bag contains 12 red roses only. Shalini takes out one rose without Looking into the bag. The probability that she takes out an orange rose is:
A)
\[\frac{1}{2}\] done
clear
B)
0 done
clear
C)
1 done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer100)
Two different coins are tossed simultaneously. The probability of getting at least one tail is:
A)
\[\frac{1}{4}\] done
clear
B)
\[\frac{1}{8}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{7}{8}\] done
clear
View Solution play_arrow
-
question_answer101)
Two dice are thrown. What is the probability that the sum of the numbers appearing on the dice is 7?
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{4}{9}\] done
clear
C)
\[\frac{5}{36}\] done
clear
D)
\[\frac{7}{36}\] done
clear
View Solution play_arrow
-
question_answer102)
| From a pack of 52 playing cards, a card is drawn at random. |
| The probability that the drawn card is not a face card, is: |
A)
\[\frac{3}{13}\] done
clear
B)
\[\frac{9}{13}\] done
clear
C)
\[\frac{10}{13}\] done
clear
D)
\[\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer103)
A card is accidently dropped, from a pack of 52 playing cards. The probability that it is a red card is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{13}\] done
clear
C)
\[\frac{1}{52}\] done
clear
D)
\[\frac{12}{13}\] done
clear
View Solution play_arrow
-
question_answer104)
If a letter of English alphabet is chosen at random, then the probability that the Letter is a consonant, is:
A)
\[\frac{5}{26}\] done
clear
B)
\[\frac{21}{26}\] done
clear
C)
\[\frac{10}{26}\] done
clear
D)
\[\frac{4}{26}\] done
clear
View Solution play_arrow
-
question_answer105)
In a single throw of a pair of dice, the probability of getting the sum as a perfect square is:
A)
\[\frac{7}{36}\] done
clear
B)
\[\frac{5}{36}\] done
clear
C)
\[\frac{8}{36}\] done
clear
D)
\[\frac{11}{36}\] done
clear
View Solution play_arrow
-
question_answer106)
In a throw of a pair of dice, what is the probability a getting a doublet?
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{6}\] done
clear
C)
\[\frac{5}{12}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer107)
Two coins are tossed simultaneously. The probability of getting at most one tail is:
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{1}{9}\] done
clear
D)
\[\frac{1}{6}\] done
clear
View Solution play_arrow
-
question_answer108)
A box contains 100 discs, numbered from 1 to 100. If one disc is drawn at random from the box, then the probability that it bears a prime number less than 30 is
A)
\[\frac{7}{100}\] done
clear
B)
\[\frac{1}{10}\] done
clear
C)
\[\frac{4}{50}\] done
clear
D)
\[\frac{9}{50}\] done
clear
View Solution play_arrow
-
question_answer109)
A card is drawn from a pack of 52 cards. The probability of drawing a black face card is:
A)
\[\frac{2}{13}\] done
clear
B)
\[\frac{3}{26}\] done
clear
C)
\[\frac{1}{13}\] done
clear
D)
\[\frac{3}{52}\] done
clear
View Solution play_arrow
-
question_answer110)
Two friends were born in the year 1996. The probability that they have the same birth date is:
A)
\[\frac{1}{183}\] done
clear
B)
\[\frac{2}{365}\] done
clear
C)
\[\frac{1}{365}\] done
clear
D)
\[\frac{1}{366}\] done
clear
View Solution play_arrow
-
question_answer111)
A number is selected at random from the numbers\[\text{2},\text{4},\text{4},\text{ 6},\text{6},\text{6},\text{ 8},\text{8},\text{8},\text{8}\]. The probability that the selected number is their average is:
A)
\[\frac{1}{10}\] done
clear
B)
\[\frac{3}{10}\] done
clear
C)
\[\frac{7}{10}\] done
clear
D)
\[\frac{9}{10}\] done
clear
View Solution play_arrow
-
question_answer112)
A bag contains 6 green balls and n yellow balls. If probability of drawing a yellow ball is five times that of a green ball, then n is equal to:
A)
10 done
clear
B)
20 done
clear
C)
30 done
clear
D)
40 done
clear
View Solution play_arrow
-
question_answer113)
A bag contains 24 balls of which x are red, \[\text{2x}\] are white and \[\text{3x}\] are blue. A ball is selected at random. What is the probability that the drawn ball is white or blue?
A)
\[1/2\] done
clear
B)
2 done
clear
C)
\[5/6\] done
clear
D)
\[7/12\] done
clear
View Solution play_arrow
-
question_answer114)
A number is selected from first 50 natural numbers. What is the probabilite that it is a multiple of 4 or 5?
A)
\[\frac{9}{25}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{6}{25}\] done
clear
D)
\[\frac{23}{50}\] done
clear
View Solution play_arrow
-
question_answer115)
A bag contains 4 red, 5 black and 3 yellow balls. A ball is taken out of the bag at random. Find the probability that the ball taken out is not of yellow colour.
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer116)
A number is selected at random from the numbers \[\text{2},\text{3},\text{3},\text{5},\text{5},\text{5},\text{7},\text{7},\text{7},\text{7,9},\text{9},\text{9},\text{9},\text{9}\] at random. Find the probability that the selected number is their median.
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{4}{15}\] done
clear
C)
\[\frac{3}{5}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer117)
If a number x is chosen from the numbers 1, 2, 3 and a number y is selected from the numbers 1. 4, 9. Then \[P(xy<8)\] is
A)
\[\frac{7}{9}\] done
clear
B)
\[\frac{5}{9}\] done
clear
C)
\[\frac{2}{3}\] done
clear
D)
\[\frac{4}{9}\] done
clear
View Solution play_arrow
-
question_answer118)
In a family of 3 children, the probability of having at Least one boy is:
A)
\[\frac{7}{8}\] done
clear
B)
\[\frac{1}{8}\] done
clear
C)
\[\frac{5}{8}\] done
clear
D)
\[\frac{3}{4}\] done
clear
View Solution play_arrow
-
question_answer119)
A card is drawn from a well shuffled pack of 52 playing cards. The probability that the card is a red or a club is:
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{3}{4}\] done
clear
D)
\[\frac{3}{13}\] done
clear
View Solution play_arrow
-
question_answer120)
If a number x is chosen at random from the numbers \[-\text{3},-\text{2},-\text{1},0,\text{1},\text{2},\text{3},\] then the probability of \[{{x}^{2}}<4\] is: (CBSE 2020)
A)
\[\frac{3}{7}\] done
clear
B)
\[\frac{2}{7}\] done
clear
C)
\[\frac{1}{7}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer121)
A card is drawn from a well shuffled pack of 52 playing cards. The probability that the card is a black or a club is:
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{3}{13}\] done
clear
View Solution play_arrow
-
question_answer122)
There are 25 tickets bearing numbers from 1 to 25. One ticket is drawn at random. The probability that the number on it is a multiple of 5 or 6 is:
A)
\[\frac{7}{25}\] done
clear
B)
\[\frac{9}{25}\] done
clear
C)
\[\frac{11}{12}\] done
clear
D)
\[\frac{13}{25}\] done
clear
View Solution play_arrow
-
question_answer123)
A bag contains 5 black balls, 4 white balls and 3 red balls If a ball is selected random wise, the probability that it is a black or red ball is:
A)
\[\frac{1}{3}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{5}{12}\] done
clear
D)
\[\frac{2}{3}\] done
clear
View Solution play_arrow
-
question_answer124)
Tickets are numbered from 1 to 100. They are well shuffled and a ticket is drawn at random. Probability that the drawn ticket has a number 5 or multiple of 5 is:
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{5}\] done
clear
C)
\[\frac{1}{25}\] done
clear
D)
\[\frac{3}{25}\] done
clear
View Solution play_arrow
-
question_answer125)
A man is known to speak truth 3 out of 4 times. He throws die and a number other than six comes up. Find the probability that he reports it is a six.
A)
\[\frac{3}{4}\] done
clear
B)
\[\frac{1}{4}\] done
clear
C)
\[\frac{1}{2}\] done
clear
D)
1 done
clear
View Solution play_arrow
-
question_answer126)
A man is known to speak truth 5 out of 7 times. He draws face card from a pack of 52 playing cards. Find the probability that he reports it is a face card.
A)
\[\frac{2}{7}\] done
clear
B)
\[\frac{3}{13}\] done
clear
C)
\[\frac{5}{7}\] done
clear
D)
\[\frac{10}{13}\] done
clear
View Solution play_arrow
-
question_answer127)
A box contains 30 chocolates in all out of which some are milk chocolates and the remaining are coco chocolates. One chocolate is taken out at random from the box and the probability that it is a milk chocolate is -, then the number coco chocolates in the box is:
A)
10 done
clear
B)
20 done
clear
C)
30 done
clear
D)
15 done
clear
View Solution play_arrow
-
question_answer128)
A bag contains 10 red flags and some green flags. If the probability of drawing a green flag is thrice that of drawing a red flag, then the number of green flags in the bag is:
A)
10 done
clear
B)
20 done
clear
C)
30 done
clear
D)
3 done
clear
View Solution play_arrow
-
question_answer129)
A purse contains 10 notes of Rs.1000, 20 notes of Rs.500 and 20 notes of Rs.100. One note is drawn at random. What is the probability that the note of Rs.500?
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{2}{5}\] done
clear
C)
\[\frac{3}{5}\] done
clear
D)
\[\frac{4}{5}\] done
clear
View Solution play_arrow
-
question_answer130)
Cards each marked with one of the numbers \[\text{4},\text{5},\text{6},.......\text{ 2}0\]are placed in a box and mixed thoroughly. One card is drawn at random from the box. What is the probability of getting an even prime number?
A)
0 done
clear
B)
1 done
clear
C)
\[-1\] done
clear
D)
\[\frac{1}{2}\] done
clear
View Solution play_arrow
-
question_answer131)
A number x is chosen at random from \[-\text{4},-\text{3},-\text{2},-\text{1},0,\text{1},\text{2},\text{3},\text{4}\] Find the probability that \[|x|\le 4\].
A)
0 done
clear
B)
1 done
clear
C)
\[\frac{1}{2}\] done
clear
D)
\[\frac{1}{9}\] done
clear
View Solution play_arrow
-
question_answer132)
| A dies is in the shape of a tetrahedron as shown in the following figure. On each face, one of the numbers 1, 2, 3 or 4 is written. |
| This die is tossed. Find the probability of getting a prime number. |
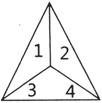 |
A)
\[\frac{1}{2}\] done
clear
B)
\[\frac{1}{3}\] done
clear
C)
1 done
clear
D)
0 done
clear
View Solution play_arrow
-
question_answer133)
| Suppose you drop a die at random on the rectangular region shown in the figure given below. What is the probability that it will Land inside the square of side \[1\,cm\]? |
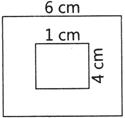 |
A)
\[\frac{1}{6}\] done
clear
B)
\[\frac{1}{12}\] done
clear
C)
\[\frac{1}{10}\] done
clear
D)
\[\frac{1}{24}\] done
clear
View Solution play_arrow
-
question_answer134)
A bag contains 8 red balls and some blue balls. If the probability of drawing a blue ball is three times of a red ball, then the number of blue balls in the bag:
A)
12 done
clear
B)
18 done
clear
C)
24 done
clear
D)
36 done
clear
View Solution play_arrow
-
question_answer135)
Ramesh buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random a tank containing 5 male fish and 9 female fish. Then, the probability that the fish taken out is a male fish, is:
A)
\[\frac{5}{13}\] done
clear
B)
\[\frac{5}{14}\] done
clear
C)
\[\frac{6}{13}\] done
clear
D)
\[\frac{7}{13}\] done
clear
View Solution play_arrow
-
question_answer136)
A letter is chosen at random from the Letters of the word 'ASSASSINATION', then the probability that the letter chosen is a vowel is in the form of \[\frac{6}{2x+1},\] then x is equal to:
A)
5 done
clear
B)
6 done
clear
C)
7 done
clear
D)
8 done
clear
View Solution play_arrow
-
question_answer137)
If a letter is chosen at random from the letter of English alphabet, then the probability that it is a letter of the word DELHI' is:
A)
\[\frac{1}{5}\] done
clear
B)
\[\frac{1}{26}\] done
clear
C)
\[\frac{5}{26}\] done
clear
D)
\[\frac{21}{26}\] done
clear
View Solution play_arrow
