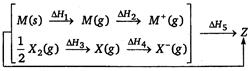question_answer 1) Solar spectrum is an example for
A)
line emission spectrum
done
clear
B)
continuous emission spectrum
done
clear
C)
band absorption spectrum
done
clear
D)
line absorption spectrum
done
clear
View Answer play_arrow
question_answer 2) When a piece of metal is illuminated by a monochromatic light of wavelength \[\lambda \], then stopping potential is \[3{{V}_{s}}\]. When same surface is illuminated by light of wavelength \[2\lambda \], then stopping potential becomes \[{{V}_{s}}\]. The value of threshold wavelength for photoelectric emission will be
A)
\[4\lambda \]
done
clear
B)
\[8\lambda \]
done
clear
C)
\[\frac{4}{3}\lambda \]
done
clear
D)
\[6\lambda \]
done
clear
View Answer play_arrow
question_answer 3) The maximum kinetic energy of emitted electrons in a photoelectric effect does not depend upon
A)
wavelength
done
clear
B)
frequency
done
clear
C)
intensity
done
clear
D)
work function
done
clear
View Answer play_arrow
question_answer 4) The ratio of minimum wavelengths of Lyman and Balmer series will be
A)
1.25
done
clear
B)
0.25
done
clear
C)
5
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 5) Hydrogen atom does not emit X-rays because
A)
it contains only a single electron
done
clear
B)
energy levels in it are far apart
done
clear
C)
its size is very small
done
clear
D)
energy levels in it are very close to each other
done
clear
View Answer play_arrow
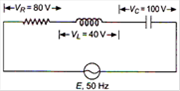
question_answer 6)
The potential difference between A and B in the following figure is
A)
32 V
done
clear
B)
48 V
done
clear
C)
24 V
done
clear
D)
14 V
done
clear
View Answer play_arrow
question_answer 7) The magnetic field at the centre of a circular current carrying conductor of radius r is \[{{B}_{c}}\]. The magnetic field on its axis at a distance r from the centre is \[{{B}_{a}}\]. The value of \[{{B}_{c}}:{{B}_{a}}\] will be
A)
\[1:\sqrt{2}\]
done
clear
B)
\[1:2\sqrt{2}\]
done
clear
C)
\[2\sqrt{2}:1\]
done
clear
D)
\[\sqrt{2}:1\]
done
clear
View Answer play_arrow
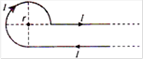
question_answer 8)
Current \[I\] is flowing in conductor shaped as shown in the figure. The radius of the curved part is r and the length of straight portion is very large. The value of the magnetic field at the centre O will be
A)
\[\frac{{{\mu }_{0}}I}{4\pi r}\left( \frac{3\pi }{2}+1 \right)\]
done
clear
B)
\[\frac{{{\mu }_{0}}I}{4\pi r}\left( \frac{3\pi }{2}-1 \right)\]
done
clear
C)
\[\frac{{{\mu }_{0}}I}{4\pi r}\left( \frac{\pi }{2}+1 \right)\]
done
clear
D)
\[\frac{{{\mu }_{0}}I}{4\pi r}\left( \frac{\pi }{2}-1 \right)\]
done
clear
View Answer play_arrow
question_answer 9) Two tangent galvanometers A and B are identical except in their number of rums. They are connected in series. On passing a current through them, deflections of \[{{60}^{o}}\] and \[{{30}^{o}}\] are produced. The ratio of the number of rums in A and B is
A)
\[1:3\]
done
clear
B)
\[3:1\]
done
clear
C)
\[1:2\]
done
clear
D)
\[2:1\]
done
clear
View Answer play_arrow
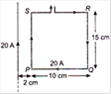
question_answer 10)
The resultant force on the current loop PQRS due to a long current carrying conductor will be
A)
\[{{10}^{-4}}N\]
done
clear
B)
\[3.6\times {{10}^{-4}}N\]
done
clear
C)
\[1.8\times {{10}^{-4}}N\]
done
clear
D)
\[5\times {{10}^{-4}}N\]
done
clear
View Answer play_arrow
question_answer 11) How many \[6\mu F\], 200 V condensers are needed to make a condenser of \[18\mu F\], 600 V?
A)
9
done
clear
B)
18
done
clear
C)
3
done
clear
D)
27
done
clear
View Answer play_arrow
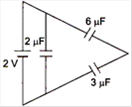
question_answer 12)
The total energy stored in the condenser system shown in the figure will be
A)
\[2\mu J\]
done
clear
B)
\[4\mu J\]
done
clear
C)
\[8\mu J\]
done
clear
D)
\[16\mu J\]
done
clear
View Answer play_arrow
question_answer 13) A metal wire is subjected to a constant potential difference. When the temperature of the metal wire increases, the drift velocity of the electron in it
A)
increases, thermal velocity of the electron decreases
done
clear
B)
decreases, thermal velocity of the electron decreases
done
clear
C)
increases, thermal velocity of the electron increases
done
clear
D)
decreases, thermal velocity of the electron increases
done
clear
View Answer play_arrow
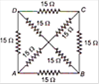
question_answer 14)
The equivalent resistance between the points A and B will be (each resistance is \[10\sqrt{3}\,kgwt\])
A)
\[30\,\Omega \]
done
clear
B)
\[8\,\Omega \]
done
clear
C)
\[10\,\Omega \]
done
clear
D)
\[40\,\Omega \]
done
clear
View Answer play_arrow
question_answer 15) In the Bohr model of hydrogen atom, the electron is pictured to rotate in a circular orbit of radius \[5\times {{10}^{-11}}m\], at a speed \[2.2\times {{10}^{6}}m/s\]. What is the current associated with electron motion?
A)
1.12 mA
done
clear
B)
3 mA
done
clear
C)
0.75 mA
done
clear
D)
2.25 mA
done
clear
View Answer play_arrow
question_answer 16) A certain current on passing through a galvanometer produces a deflection of 100 divisions. When a shunt of one ohm is connected, the deflection reduces to 1 division. The galvanometer resistance is
A)
\[100\,\Omega \]
done
clear
B)
\[99\,\Omega \]
done
clear
C)
\[10\,\Omega \]
done
clear
D)
\[9.9\,\Omega \]
done
clear
View Answer play_arrow
question_answer 17) Two similar circular loops carry equal current in the same direction. On moving coils further apart, the electric current will
A)
increase in both
done
clear
B)
decrease in both
done
clear
C)
remain unaltered
done
clear
D)
increases in one and decreases in the second
done
clear
View Answer play_arrow
question_answer 18)
The value of alternating emf E in the given circuit will be
A)
220 V
done
clear
B)
140 V
done
clear
C)
100 V
done
clear
D)
20 V
done
clear
View Answer play_arrow
question_answer 19) A current of 5 A is flowing at 220 V in the primary coil of a transformer. If the voltage produced in the secondary coil is 2200 V and 50% of power is lost, then the current secondary will be
A)
2.5 A
done
clear
B)
5 A
done
clear
C)
0.25 A
done
clear
D)
0.5 A
done
clear
View Answer play_arrow
question_answer 20) For a series LCR circuit at resonance, the statement which is not true is
A)
Peak energy stored by a capacitor = peak energy stored by an inductor.
done
clear
B)
Average power = apparent power.
done
clear
C)
Watt less current is zero.
done
clear
D)
Power factor is zero.
done
clear
View Answer play_arrow
question_answer 21) If \[{{\mu }_{0}}\] is permeability of free space and \[{{\varepsilon }_{0}}\] is permittivity of free space, the speed of light in vacuum is given by
A)
\[\sqrt{{{\mu }_{0}}{{\varepsilon }_{0}}}\]
done
clear
B)
\[\sqrt{\frac{{{\mu }_{0}}}{{{\varepsilon }_{0}}}}\]
done
clear
C)
\[\sqrt{\frac{1}{{{\varepsilon }_{0}}{{\mu }_{0}}}}\]
done
clear
D)
\[\sqrt{\frac{{{\varepsilon }_{0}}}{{{\mu }_{0}}}}\]
done
clear
View Answer play_arrow
question_answer 22) In Young's double slit experiment, a third slit is made in between the double slits. Then
A)
intensity of fringes totally disappears
done
clear
B)
only bright light is observed on the screen
done
clear
C)
fringes of unequal width are formed
done
clear
D)
contrast between bright and dark fringes is reduced
done
clear
View Answer play_arrow
question_answer 23) In a two slit experiment with monochromatic light fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by \[5\times {{10}^{-2}}m\] towards the slits, the change in fringe width is \[3\times {{10}^{-5}}m\]. If separation between the slits is \[{{10}^{-3}}m\], the wavelength of light used is
A)
\[6000\,\,\overset{o}{\mathop{A}}\,\]
done
clear
B)
\[5000\,\,\overset{o}{\mathop{A}}\,\]
done
clear
C)
\[3000\,\,\overset{o}{\mathop{A}}\,\]
done
clear
D)
\[4500\,\,\overset{o}{\mathop{A}}\,\]
done
clear
View Answer play_arrow
question_answer 24) In a Fraunhofer diffraction experiment at a single slit using a light of wavelength 400 nm, the first minimum is formed at an angle of \[{{30}^{o}}\]. The direction 6 of the first secondary maximum is given by
A)
\[{{\sin }^{-1}}\left( \frac{2}{3} \right)\]
done
clear
B)
\[{{\sin }^{-1}}\left( \frac{3}{4} \right)\]
done
clear
C)
\[{{\sin }^{-1}}\left( \frac{1}{4} \right)\]
done
clear
D)
\[ta{{n}^{-1}}\left( \frac{2}{3} \right)\]
done
clear
View Answer play_arrow
question_answer 25) Maximum diffraction takes place in a given slit for
A)
\[\gamma \]-rays
done
clear
B)
ultraviolet light
done
clear
C)
infrared light
done
clear
D)
radio waves
done
clear
View Answer play_arrow
question_answer 26) If an electron and a proton have the same de Broglie wavelength, then the kinetic energy of the electron is
A)
zero
done
clear
B)
less than that of a proton
done
clear
C)
more than that of a proton
done
clear
D)
equal to that of a proton
done
clear
View Answer play_arrow
question_answer 27) Two protons are kept at a separation of 40 \[{{A}^{o}}\] is the nuclear force and \[{{F}_{e}}\] is the electrostatic force between them. Then
A)
\[{{F}_{n}}>>{{F}_{e}}\]
done
clear
B)
\[{{F}_{n}}={{F}_{e}}\]
done
clear
C)
\[{{F}_{n}}<<{{F}_{e}}\]
done
clear
D)
\[{{F}_{n}}\approx {{F}_{e}}\]
done
clear
View Answer play_arrow
question_answer 28) Blue colour of sea water is due to
A)
interference of sunlight reflected from the water surface
done
clear
B)
scattering of sunlight by the water molecules
done
clear
C)
image of sky in water
done
clear
D)
refraction of sunlight
done
clear
View Answer play_arrow
question_answer 29) The ratio of the nuclear radii of elements with mass numbers 216 and 125 is
A)
\[216:125\]
done
clear
B)
\[\sqrt{216}:\sqrt{125}\]
done
clear
C)
\[6:5\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 30) On bombarding \[{{U}^{235}}\] by slow neutron, 200 MeV energy is released, if the power output of atomic reactor is 1.6 MW, then the rate of fission will be
A)
\[5\times {{10}^{22}}/s\]
done
clear
B)
\[5\times {{10}^{16}}/s\]
done
clear
C)
\[8\times {{10}^{16}}/s\]
done
clear
D)
\[20\times {{10}^{16}}/s\]
done
clear
View Answer play_arrow
question_answer 31) A ray of light enters from a rarer to a denser medium. The angle of incidence is \[i\]. Then the reflected and refracted rays are mutually perpendicular to each other. The critical angle for the pair of media is
A)
\[{{\sin }^{-1}}(\tan i)\]
done
clear
B)
\[{{\tan }^{-1}}(\sin i)\]
done
clear
C)
\[{{\sin }^{-1}}(\cot i)\]
done
clear
D)
\[{{\cos }^{-1}}(\tan i)\]
done
clear
View Answer play_arrow
question_answer 32) A fish in water (refractive index n) looks at a bird vertically above in the air. If y is the height of the bird and \[x\] is the depth of the fish from the surface, then the distance of the bird as estimated by the fish is
A)
\[x+y\left( 1-\frac{1}{n} \right)\]
done
clear
B)
\[x+ny\]
done
clear
C)
\[x+y\left( 1+\frac{1}{n} \right)\]
done
clear
D)
\[y+x\left( 1-\frac{1}{n} \right)\]
done
clear
View Answer play_arrow
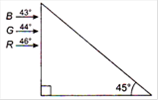
question_answer 33)
Figure shows a mixture of blue, green and red colored rays incident normally on a right angled prism. The critical angles of the material of the prism for red, green and blue are \[{{46}^{o}},{{44}^{o}}\] and \[{{43}^{o}}\] respectively. The arrangement will separate
A)
red colour from blue and green
done
clear
B)
blue colour from red and green
done
clear
C)
green colour from red and blue
done
clear
D)
all the three colours
done
clear
View Answer play_arrow
question_answer 34) A convex and a concave lens separated by distance d are then put in contact. The focal length of the combination
A)
decreases
done
clear
B)
increases
done
clear
C)
becomes
done
clear
D)
remains the same
done
clear
View Answer play_arrow
question_answer 35)
A convex lens is made of 3 layers of glass of 3 different materials as in the figures. A point object is placed on its axis. The number of images of the object are
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 36) An unpolarised beam of intensity \[{{I}_{0}}\] falls on a polarold. The intensity of the emergent light is
A)
\[\frac{{{I}_{0}}}{2}\]
done
clear
B)
\[{{I}_{0}}\]
done
clear
C)
\[\frac{{{I}_{0}}}{4}\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 37) Which of the following as a dichroic crystal?
A)
Quartz
done
clear
B)
Tourmaline
done
clear
C)
Mica
done
clear
D)
Selenite
done
clear
View Answer play_arrow
question_answer 38) Two identical metal spheres charged with \[+12\mu F\] and \[-8\mu F\] are kept at certain distance in air. They are brought into contact and then kept at the same distance. The ratio of the magnitudes of electrostatic forces between them before and after contact is
A)
\[12:1\]
done
clear
B)
\[8:1\]
done
clear
C)
\[24:1\]
done
clear
D)
\[4:1\]
done
clear
View Answer play_arrow
question_answer 39) A small conducting sphere of radius r is lying concentrically inside a bigger hollow conducting sphere of radius R. The bigger and smaller spheres are charged with Q and \[q\,(Q>q)\] and are insulated from each other. The potential difference between the spheres will be
A)
\[\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{q}{r}-\frac{q}{R} \right)\]
done
clear
B)
\[\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{q}{R}-\frac{Q}{r} \right)\]
done
clear
C)
\[\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{q}{r}-\frac{Q}{R} \right)\]
done
clear
D)
\[\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{Q}{R}+\frac{q}{r} \right)\]
done
clear
View Answer play_arrow
question_answer 40) The charges Q, +q and +q are placed at the vertices of an equilateral triangle of side \[l\]. If the net electrostatic potential energy of the system is zero, then Q is equal to
A)
\[-\frac{q}{2}\]
done
clear
B)
\[-q\]
done
clear
C)
\[\frac{+q}{2}\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 41) Dimensional formula for the universal gravitational constant G is
A)
\[[{{M}^{-1}}{{L}^{2}}{{T}^{-2}}]\]
done
clear
B)
\[[{{M}^{0}}{{L}^{0}}{{T}^{0}}]\]
done
clear
C)
\[[{{M}^{-1}}{{L}^{3}}{{T}^{-2}}]\]
done
clear
D)
\[[{{M}^{-1}}{{L}^{3}}{{T}^{-1}}]\]
done
clear
View Answer play_arrow
question_answer 42) A body is projected vertically upwards. The times corresponding to height h while ascending and while descending are \[{{t}_{1}}\] and \[{{t}_{2}}\]respectively Then the velocity of projection is (g is acceleration due to gravity)
A)
\[g\sqrt{{{t}_{1}}{{t}_{2}}}\]
done
clear
B)
\[\frac{g{{t}_{1}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\]
done
clear
C)
\[\frac{g\sqrt{{{t}_{1}}{{t}_{2}}}}{2}\]
done
clear
D)
\[\frac{g\,({{t}_{1}}+{{t}_{2}})}{2}\]
done
clear
View Answer play_arrow
question_answer 43) A mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of \[{{60}^{o}}\] with the vertical The new reading of the balance is
A)
20 kg - wt
done
clear
B)
10 kg - wt
done
clear
C)
\[10\sqrt{3}\,kgwt\]
done
clear
D)
\[20\sqrt{3}\,kg-wt\]
done
clear
View Answer play_arrow
question_answer 44) A body weighs 50 gin air and 40 gin water. How much would it weigh in a liquid of specific gravity 1.5?
A)
30 g
done
clear
B)
35 g
done
clear
C)
65 g
done
clear
D)
45 g
done
clear
View Answer play_arrow
question_answer 45) A body of mass 4 kg is accelerated upon b constant force, travels a distance of 5 m in the first second and a distance of 2 m in the third second. The force acting on the body is
A)
2 N
done
clear
B)
4 N
done
clear
C)
6 N
done
clear
D)
8 N
done
clear
View Answer play_arrow
question_answer 46) A simple pendulum is suspended from the ceiling of a lift. When the lift is at rest its time period is T. With what acceleration should lift be accelerated upwards in order to reduce its period to T/2? (g is acceleration due to gravity).
A)
2 g
done
clear
B)
3 g
done
clear
C)
4 g
done
clear
D)
g
done
clear
View Answer play_arrow
question_answer 47) If y is the ratio of specific heats and R is the universal gas constant, then the molar specific heat at constant volume C is given by
A)
\[\gamma R\]
done
clear
B)
\[\frac{(\gamma -1)R}{\gamma }\]
done
clear
C)
\[\frac{R}{\gamma -1}\]
done
clear
D)
\[\frac{\gamma R}{\gamma -1}\]
done
clear
View Answer play_arrow
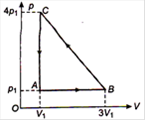
question_answer 48)
An ideal gas is taken via path ABCA as shown in figure. The net work done in the whole cycle is
A)
\[3{{p}_{1}}{{V}_{1}}\]
done
clear
B)
\[-3{{p}_{1}}{{V}_{1}}\]
done
clear
C)
\[6{{p}_{1}}{{V}_{1}}\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 49) In which of the processes, does the internal energy of the system remain constant?
A)
Adiabatic
done
clear
B)
Isochoric
done
clear
C)
Isobaric
done
clear
D)
Isothermal
done
clear
View Answer play_arrow
question_answer 50)
The coefficient of thermal conductivity of copper is 9 times that of steel. In the composite cylindrical bar shown in the figure, what will be the temperature at the junction of copper and steel?
A)
\[{{75}^{o}}C\]
done
clear
B)
\[{{67}^{o}}C\]
done
clear
C)
\[{{25}^{o}}C\]
done
clear
D)
\[{{33}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 51) The equation of a simple harmonic wave is given by \[y=6\text{ }\sin \text{ }2\pi \,(2t-0.1x)\] where \[x\] and y are in mm and t is in seconds. The phase difference between two particles 2 mm apart at any instant is
A)
\[{{18}^{o}}\]
done
clear
B)
\[{{36}^{o}}\]
done
clear
C)
\[{{54}^{o}}\]
done
clear
D)
\[{{72}^{o}}\]
done
clear
View Answer play_arrow
question_answer 52) With what velocity should an observer approach a stationary sound source, so that the apparent frequency of sound should appear double the actual frequency? (v is velocity of sound).
A)
\[\frac{v}{2}\]
done
clear
B)
3 v
done
clear
C)
2 v
done
clear
D)
v
done
clear
View Answer play_arrow
question_answer 53) If a black body emits 0.5 J of energy per second when it is at \[{{27}^{o}}C\], then the amount of energy emitted by it when it is at \[{{627}^{o}}C\] will be
A)
40.5 J
done
clear
B)
162 J
done
clear
C)
13.5 J
done
clear
D)
135 J
done
clear
View Answer play_arrow
question_answer 54) A string vibrates with a frequency of 200 Hz. When its length is doubled and tension is altered, it begins to vibrate with a frequency of 300 Hz. The ratio of the new tension to the original tension is
A)
\[9:1\]
done
clear
B)
\[1:9\]
done
clear
C)
\[3:1\]
done
clear
D)
\[1:3\]
done
clear
View Answer play_arrow
question_answer 55) How many times more intense is a 60 dB sound than a 30 dB sound?
A)
1000
done
clear
B)
2
done
clear
C)
100
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 56) The masses of two radioactive substances are same and their half-lives are 1 yr and 2 yr respectively. The ratio of their activities after 4 yr will be
A)
\[1:4\]
done
clear
B)
\[1:2\]
done
clear
C)
\[1:3\]
done
clear
D)
\[1:6\]
done
clear
View Answer play_arrow
question_answer 57) \[_{92}{{U}^{235}}\] undergoes successive disintegrations with the end product of \[_{82}P{{b}_{203}}\]. The number of \[\alpha \] and \[\beta \] particles emitted are
A)
\[\alpha =6,~\beta =4\]
done
clear
B)
\[\alpha =6,~\beta =0\]
done
clear
C)
\[\alpha =8,~\beta =6\]
done
clear
D)
\[\alpha =3,~\beta =3\]
done
clear
View Answer play_arrow
question_answer 58) The most stable particle in Baryon group is
A)
neutron
done
clear
B)
omega-particle
done
clear
C)
proton
done
clear
D)
lambda-particle
done
clear
View Answer play_arrow
question_answer 59) In an unbiased p-n junction
A)
Potential at p is more than that at n
done
clear
B)
Potential at p is less than that at n
done
clear
C)
Potential at p is equal to that at n
done
clear
D)
Potential at p is +ve and that at n is -ve
done
clear
View Answer play_arrow
question_answer 60)
To get an output \[Y=1\] from the circuit shown, the inputs A, B and C must be respectively
A)
0, 1, 0
done
clear
B)
1, 0, 0
done
clear
C)
1, 0, 1
done
clear
D)
1, 1, 0
done
clear
View Answer play_arrow
question_answer 61) The number of nodal planes present in \[{{\sigma }^{*}}s\] anti bonding orbitals is
A)
1
done
clear
B)
2
done
clear
C)
0
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 62) Which of the following electrolytic solutions has the least specific conductance?
A)
0.02 N
done
clear
B)
0.2 N
done
clear
C)
2 N
done
clear
D)
0.002 N
done
clear
View Answer play_arrow
question_answer 63) The overlapping of orbitals in benzene is of the type
A)
\[sp-sp\]
done
clear
B)
\[p-p\]
done
clear
C)
\[s{{p}^{2}}-s{{p}^{2}}\]
done
clear
D)
\[s{{p}^{3}}-s{{p}^{3}}\]
done
clear
View Answer play_arrow
question_answer 64) The calculated bond order of superoxide ion \[(CO_{2}^{-})\] is
A)
2.5
done
clear
B)
2
done
clear
C)
1.5
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 65) Which of the following can be measured by the Ostwald-Walker dynamic method?
A)
Relative lowering of vapour pressure
done
clear
B)
Lowering of vapour pressure
done
clear
C)
Vapour pressure of the solvent
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 66) Mesomeric effect involves delocalization of
A)
pi electrons
done
clear
B)
sigma electrons
done
clear
C)
protons
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 67) Which of the following has the maximum number of unpaired 'd' electrons?
A)
\[Z{{n}^{2+}}\]
done
clear
B)
\[F{{e}^{2+}}\]
done
clear
C)
\[N{{i}^{3+}}\]
done
clear
D)
\[C{{u}^{+}}\]
done
clear
View Answer play_arrow
question_answer 68) One mole of which of the following has the highest entropy?
A)
Liquid nitrogen
done
clear
B)
Hydrogen gas
done
clear
C)
Mercury
done
clear
D)
Diamond
done
clear
View Answer play_arrow
question_answer 69) Which of the following species does not exert a resonance effect?
A)
\[{{C}_{6}}{{H}_{5}}N{{H}_{2}}\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}\overset{+}{\mathop{N}}\,{{H}_{3}}\]
done
clear
C)
\[{{C}_{6}}{{H}_{5}}OH\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}Cl\]
done
clear
View Answer play_arrow
question_answer 70) A complex compound in which the oxidation number of a metal is zero is
A)
\[{{K}_{4}}[Fe{{(CN)}_{6}}]\]
done
clear
B)
\[{{K}_{3}}[Fe{{(CN)}_{6}}]\]
done
clear
C)
\[[Ni{{(CO)}_{4}}]\]
done
clear
D)
\[[Pt{{(N{{H}_{3}})}_{4}}]C{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 71) Catalytic dehydrogenation of a primary alcohol gives a
A)
secondary alcohol
done
clear
B)
aldehyde
done
clear
C)
ketone
done
clear
D)
ester
done
clear
View Answer play_arrow
question_answer 72) Excess of \[PC{{l}_{5}}\] reacts with cone \[{{H}_{2}}S{{O}_{4}}\] giving
A)
chlorosulphonic acid
done
clear
B)
thionyl chloride
done
clear
C)
sulphuryl chloride
done
clear
D)
sulphurous acid
done
clear
View Answer play_arrow
question_answer 73) If one mole of ammonia and one mole of hydrogen chloride are mixed in a closed container to form ammonium chloride gas, then
A)
\[\Delta H>\Delta U\]
done
clear
B)
\[\Delta H=\Delta U\]
done
clear
C)
\[\Delta H<\Delta U\]
done
clear
D)
there is no relationship
done
clear
View Answer play_arrow
question_answer 74) The compound on dehydrogenation gives a ketone. The original compound is
A)
primary alcohol
done
clear
B)
secondary alcohol
done
clear
C)
tertiary alcohol
done
clear
D)
carboxylic acid
done
clear
View Answer play_arrow
question_answer 75) Which is the most easily liquifiable rare gas?
A)
Xe
done
clear
B)
Kr
done
clear
C)
Ar
done
clear
D)
Ne
done
clear
View Answer play_arrow
question_answer 76) Three moles of \[PC{{l}_{5}}\], three moles of \[PC{{l}_{3}}\]and two moles of \[C{{l}_{2}}\] are taken in a closed vessel. If at equilibrium the vessel has 1.5 moles of\[PC{{l}_{5}}\], the number of moles of \[PC{{l}_{3}}\] present in it is
A)
5
done
clear
B)
3
done
clear
C)
6
done
clear
D)
4.5
done
clear
View Answer play_arrow
question_answer 77) How many optically active stereomers are possible for butan-2,3-diol?
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 78) An octahedral complex is formed when hybrid orbitals of the following type are involved
A)
\[s{{p}^{3}}\]
done
clear
B)
\[ds{{p}^{2}}\]
done
clear
C)
\[{{d}^{2}}s{{p}^{3}}\]
done
clear
D)
\[s{{p}^{2}}{{d}^{2}}\]
done
clear
View Answer play_arrow
question_answer 79) For the reaction\[2HI(g)\rightleftarrows {{H}_{2}}(g)+{{I}_{2}}(g)-Q\,\,kJ\],the equilibrium constant depends upon
A)
temperature
done
clear
B)
pressure
done
clear
C)
catalyst
done
clear
D)
volume
done
clear
View Answer play_arrow
question_answer 80) The angle strain in cyclobutane is
A)
\[{{24}^{o}}44'\]
done
clear
B)
\[{{29}^{o}}16'\]
done
clear
C)
\[{{19}^{o}}22'\]
done
clear
D)
\[{{9}^{o}}44'\]
done
clear
View Answer play_arrow
question_answer 81) Methoxy methane and ethanol are
A)
position isomers
done
clear
B)
chain isomers
done
clear
C)
functional isomers
done
clear
D)
optical isomers
done
clear
View Answer play_arrow
question_answer 82) When the azimuthal quantum number has the value of 2, the number of orbitals possible are
A)
7
done
clear
B)
5
done
clear
C)
3
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 83) For the reaction \[F{{e}_{2}}{{O}_{3}}+3CO\xrightarrow{{}}2Fe+3C{{O}_{2}}\] the volume of carbon monoxide required to reduce one mole of ferric oxide is
A)
\[22.4\,\,d{{m}^{3}}\]
done
clear
B)
\[44.8\,\,d{{m}^{3}}\]
done
clear
C)
\[67.2\,\,d{{m}^{3}}\]
done
clear
D)
\[11.2\,\,d{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 84) The monomers of buna-S rubber are
A)
vinyl chloride and sulphur
done
clear
B)
butadiene
done
clear
C)
styrene and butadiene
done
clear
D)
isoprene and butadiene
done
clear
View Answer play_arrow
question_answer 85) An element with atomic number 21 is a
A)
halogen
done
clear
B)
representative element
done
clear
C)
transition element
done
clear
D)
alkali metal
done
clear
View Answer play_arrow
question_answer 86) n-propyl bromide on treating with alcoholic KOH produces
A)
propane
done
clear
B)
propene
done
clear
C)
propyne
done
clear
D)
propanol
done
clear
View Answer play_arrow
question_answer 87) Mercury is a liquid metal because
A)
it has a completely filled s orbital
done
clear
B)
it has a small atomic size
done
clear
C)
it has a completely filled d orbital that prevents d-d overlapping of orbitals
done
clear
D)
it has a completely filled d orbital that causes d-d overlapping
done
clear
View Answer play_arrow
question_answer 88) A compound is formed by elements A and B. This crystallizes in the cubic structure where the A atoms are at the corners of the cube and B atoms are at the body centres. The simplest formula of the compound is
A)
AB
done
clear
B)
\[{{A}_{6}}B\]
done
clear
C)
\[{{A}_{8}}{{B}_{4}}\]
done
clear
D)
\[A{{B}_{6}}\]
done
clear
View Answer play_arrow
question_answer 89) Anisole can be prepared by the action of methyl iodide on sodium phenate. The reaction is called
A)
Wurtz's reaction
done
clear
B)
Williamson's reaction
done
clear
C)
Fittig's reaction
done
clear
D)
Etard's reaction
done
clear
View Answer play_arrow
question_answer 90) Malleability and ductility of metals can be accounted due to
A)
the presence of electrostatic force
done
clear
B)
the crystalline structure in metal
done
clear
C)
the capacity of layers of metal ions to slide over the other
done
clear
D)
the interaction of electrons with metal ions in the lattice
done
clear
View Answer play_arrow
question_answer 91) The correct order in which the first ionization potential increases is
A)
Na, K, Be
done
clear
B)
K, Na, Be
done
clear
C)
K, Be, Na
done
clear
D)
Be, Na, K
done
clear
View Answer play_arrow
question_answer 92) \[10\,\,c{{m}^{3}}\] of 0.1 N monobasic acid requires \[15\,\,c{{m}^{3}}\] of sodium hydroxide solution whose normality is
A)
1.5 N
done
clear
B)
0.15 N
done
clear
C)
0.066 N
done
clear
D)
0.66 N
done
clear
View Answer play_arrow
question_answer 93) The IUPAC name for tertiary butyl iodide is
A)
4-iodo butane
done
clear
B)
2-iodo butane
done
clear
C)
1-iodo-3-methyl propane
done
clear
D)
2-iodo-2-methyl propane
done
clear
View Answer play_arrow
question_answer 94) When sulphur dioxide is passed in an acidified\[{{K}_{2}}C{{r}_{2}}{{O}_{7}}\] solution, the oxidation state of sulphur is changed from
A)
+ 4 to 0
done
clear
B)
+ 4 to +2
done
clear
C)
+ 4 to +6
done
clear
D)
+6 to +4
done
clear
View Answer play_arrow
question_answer 95) Mass of 0.1 mole of methane is
A)
1g
done
clear
B)
16 g
done
clear
C)
1.6 g
done
clear
D)
0.1 g
done
clear
View Answer play_arrow
question_answer 96) The maximum number of hydrogen bonds that a molecule of water can have is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 97) A gas deviates from ideal behaviour at a high pressure because its molecules
A)
attract one another
done
clear
B)
show the Tyndall effect
done
clear
C)
have kinetic energy
done
clear
D)
are bound by covalent bonds
done
clear
View Answer play_arrow
question_answer 98) The reagent used to convert an alkyne to alkene is
A)
\[Zn/HCl\]
done
clear
B)
\[Sn/HCl\]
done
clear
C)
\[Zn-Hg/HCl\]
done
clear
D)
\[Pd-{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 99) When compared to \[\Delta {{G}^{o}}\] for the formation of \[A{{l}_{2}}{{O}_{3}}\], the \[\Delta {{G}^{o}}\] for the formation of \[C{{r}_{2}}{{O}_{3}}\] is
A)
higher
done
clear
B)
lower
done
clear
C)
same
done
clear
D)
unpredicted
done
clear
View Answer play_arrow
question_answer 100) In order to increase the volume of a gas by 10%, the pressure of the gas should be
A)
increased by 10%
done
clear
B)
increased by 1%
done
clear
C)
decreased by 10%
done
clear
D)
decreased by 1%
done
clear
View Answer play_arrow
question_answer 101) Helium is used in balloons in place of hydrogen because it is
A)
incombustible
done
clear
B)
lighter than hydrogen
done
clear
C)
radioactive
done
clear
D)
more abundant than hydrogen
done
clear
View Answer play_arrow
question_answer 102) The basic principle of Cottnell?s precipitator is
A)
Le-Chatelier's principle
done
clear
B)
peptisation
done
clear
C)
neutralization of charge on colloidal particles
done
clear
D)
scattering of light'
done
clear
View Answer play_arrow
question_answer 103) When carbon monoxide is passed over solid caustic soda heated to \[{{200}^{o}}C\], it forms
A)
\[N{{a}_{2}}C{{O}_{3}}\]
done
clear
B)
\[NaHC{{O}_{3}}\]
done
clear
C)
\[HCOONa\]
done
clear
D)
\[C{{H}_{3}}COONa\]
done
clear
View Answer play_arrow
question_answer 104) \[{{N}_{2}}+3{{H}_{2}}\rightleftarrows 2N{{H}_{3}}\]heat. What is the effect of the increase of temperature on the equilibrium of the reaction?
A)
Equilibrium is shifted to the left
done
clear
B)
Equilibrium is shifted to the right
done
clear
C)
Equilibrium is unaltered
done
clear
D)
Reaction rate does not change
done
clear
View Answer play_arrow
question_answer 105) Hydrogen gas is not liberated when the following metal is added to dil \[HCl\]
A)
Ag
done
clear
B)
Zn
done
clear
C)
Mg
done
clear
D)
Sn
done
clear
View Answer play_arrow
question_answer 106)
Consider the Bom-Haber cycle for the formation of an ionic compound given below and identify the compound (Z) formed.
A)
\[{{M}^{+}}{{X}^{-}}\]
done
clear
B)
\[{{M}^{+}}{{X}^{-}}(s)\]
done
clear
C)
\[MX\]
done
clear
D)
\[{{M}^{+}}{{X}^{-}}(g)\]
done
clear
View Answer play_arrow
question_answer 107) In the brown ring test, the brown colour of the ring is due to
A)
ferrous nitrate
done
clear
B)
ferric nitrate
done
clear
C)
a mixture of NO and \[N{{O}_{2}}\]
done
clear
D)
nitrosoferrous sulphate
done
clear
View Answer play_arrow
question_answer 108) Amines behave as
A)
Lewis acid
done
clear
B)
Lewis base
done
clear
C)
aprotic acid
done
clear
D)
neutral compound
done
clear
View Answer play_arrow
question_answer 109) Dalda is prepared from oils by
A)
oxidation
done
clear
B)
reduction
done
clear
C)
hydrolysis
done
clear
D)
distillation
done
clear
View Answer play_arrow
question_answer 110) The chemical name of anisole is
A)
ethanoic acid
done
clear
B)
methoxy benzene
done
clear
C)
propanone
done
clear
D)
acetone
done
clear
View Answer play_arrow
question_answer 111) The number of disulphide linkages present in insulin are
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 112) 80 g of oxygen contains as many atoms as in
A)
80 g of hydrogen
done
clear
B)
1 g of hydrogen
done
clear
C)
10 g of hydrogen
done
clear
D)
5 g of hydrogen
done
clear
View Answer play_arrow
question_answer 113) Which metal has a greater tendency to form metal oxide?
A)
Cr
done
clear
B)
Fe
done
clear
C)
Al
done
clear
D)
Ca
done
clear
View Answer play_arrow
question_answer 114) Identify the reaction that does not take place in a blast furnace.
A)
\[CaC{{O}_{3}}\xrightarrow{{}}CaO+C{{O}_{2}}\]
done
clear
B)
\[CaO+Si{{O}_{2}}\xrightarrow{{}}CaSi{{O}_{3}}\]
done
clear
C)
\[2F{{e}_{2}}{{O}_{3}}+3C\xrightarrow{{}}4Fe+3C{{O}_{2}}\]
done
clear
D)
\[C{{O}_{2}}+C\xrightarrow{{}}2CO\]
done
clear
View Answer play_arrow
question_answer 115) Waxes are esters of
A)
glycerol
done
clear
B)
long chain alcohols
done
clear
C)
glycerol and fatty acid
done
clear
D)
long chain alcohols and long chain fatty acids
done
clear
View Answer play_arrow
question_answer 116) An ionic compound is expected to have tetrahedral structure if \[{{r}_{+}}/{{r}_{-}}\] lies in the range of
A)
0.414 to 0.732
done
clear
B)
0.225 to 0.414
done
clear
C)
0.155 to 0.225
done
clear
D)
0.732 to 1
done
clear
View Answer play_arrow
question_answer 117) Among the following, which is least acidic?
A)
phenol
done
clear
B)
o-cresol
done
clear
C)
p-nitrophenol
done
clear
D)
p-chlorophenol
done
clear
View Answer play_arrow
question_answer 118) A ligand can also be regarded as
A)
Lewis acid
done
clear
B)
Bronstedbase
done
clear
C)
Lewis base
done
clear
D)
Bronsted acid
done
clear
View Answer play_arrow
question_answer 119) The colour of sky is due to
A)
transmission of light
done
clear
B)
wavelength of scattered light
done
clear
C)
absorption of light by atomspheric gases
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 120) Which of the following organic compounds answers to both iodoform test and Fehling's test?
A)
Ethanol
done
clear
B)
Methanal
done
clear
C)
Ethanal
done
clear
D)
Propanone
done
clear
View Answer play_arrow
question_answer 121) The locus of a point which moves such that the sum of its distances from two fixed points is a constant, is
A)
a circle
done
clear
B)
a parabola
done
clear
C)
an ellipse
done
clear
D)
a hyperbola
done
clear
View Answer play_arrow
question_answer 122) The centroid of the triangle ABC, where \[A\equiv (2,3),\]\[B\equiv (8,10)\] and \[C\equiv (5,5)\]is
A)
\[(5,6)\]
done
clear
B)
\[(6,5)\]
done
clear
C)
\[(6,6)\]
done
clear
D)
\[(15,18)\]
done
clear
View Answer play_arrow
question_answer 123) If \[3{{x}^{2}}+xy-{{y}^{2}}-3x+6y+k=0\] represents a pair of lines, then k is equal to
A)
\[0\]
done
clear
B)
\[9\]
done
clear
C)
\[1\]
done
clear
D)
\[-9\]
done
clear
View Answer play_arrow
question_answer 124) The equation of the smallest circle passing through the points \[(2,2)\] and \[(3,3)\] is
A)
\[{{x}^{2}}+{{y}^{2}}+5x+5y+12=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-5x-5y+12=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+5x-5y+12=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-5x+5y-12=0\]
done
clear
View Answer play_arrow
question_answer 125) The characteristic roots of the matrix \[\left[ \begin{matrix} 1 & 0 & 0 \\ 2 & 3 & 0 \\ 4 & 5 & 6 \\ \end{matrix} \right]\] are
A)
\[1,3,6\]
done
clear
B)
\[1,2,4\]
done
clear
C)
\[4,5,6\]
done
clear
D)
\[2,4,6\]
done
clear
View Answer play_arrow
question_answer 126) If \[{{e}_{1}}\] and \[{{e}_{2}}\] are the eccentricities of a hyperbola \[3{{x}^{2}}-3{{y}^{2}}=25\] and its conjugate, then
A)
\[e_{1}^{2}+e_{2}^{2}=2\]
done
clear
B)
\[e_{1}^{2}+e_{2}^{2}=4\]
done
clear
C)
\[{{e}_{1}}+{{e}_{2}}=4\]
done
clear
D)
\[{{e}_{1}}+{{e}_{2}}=\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 127) If p and q are prime numbers satisfying the condition \[{{p}^{2}}-2{{q}^{2}}=1,\] then the value of \[{{p}^{2}}+2{{q}^{2}}\]is
A)
\[5\]
done
clear
B)
\[15\]
done
clear
C)
\[16\]
done
clear
D)
\[17\]
done
clear
View Answer play_arrow
question_answer 128) If \[A(adj\,A)=5I\] where \[I\] is the identity matrix of order 3, then \[|adj\,\,A|\] is equal to
A)
\[125\]
done
clear
B)
\[25\]
done
clear
C)
\[5\]
done
clear
D)
\[10\]
done
clear
View Answer play_arrow
question_answer 129) The number of solutions for the equation \[\sin 2x+\cos 4x=2\] is
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 130) \[\int{{{e}^{x}}.{{x}^{5}}\,dx}\] is
A)
\[{{e}^{x}}[{{x}^{5}}+5{{x}^{4}}+20{{x}^{3}}+60{{x}^{2}}+120x+120]+C\]
done
clear
B)
\[{{e}^{x}}[{{x}^{5}}-5{{x}^{4}}-20{{x}^{3}}-60{{x}^{2}}-120x-120]+C\]
done
clear
C)
\[{{e}^{x}}[{{x}^{5}}-5{{x}^{4}}+20{{x}^{3}}-60{{x}^{2}}+120x-120]+C\]
done
clear
D)
\[{{e}^{x}}[{{x}^{5}}-5{{x}^{4}}+20{{x}^{3}}-60{{x}^{2}}-120x+120]+C\]
done
clear
View Answer play_arrow
question_answer 131) The equation \[\frac{{{x}^{2}}}{2-\lambda }-\frac{{{y}^{2}}}{\lambda -5}-1=0\] represents an ellipse, if
A)
\[\lambda >5\]
done
clear
B)
\[\lambda <2\]
done
clear
C)
\[2<\lambda <5\]
done
clear
D)
\[2>\lambda >5\]
done
clear
View Answer play_arrow
question_answer 132) The equation of the normal to the hyperbola \[\frac{{{x}^{2}}}{16}-\frac{{{y}^{2}}}{9}=1\] at \[(-4,0)\]is
A)
\[2x-3y=1\]
done
clear
B)
\[x=0\]
done
clear
C)
\[x=1\]
done
clear
D)
\[y=0\]
done
clear
View Answer play_arrow
question_answer 133) The converse of the contrapositive of the conditional \[p\to \tilde{\ }q\]is
A)
\[p\to q\]
done
clear
B)
\[\tilde{\ }p\to \tilde{\ }q\]
done
clear
C)
\[\tilde{\ }q\to p\]
done
clear
D)
\[\tilde{\ }p\to q\]
done
clear
View Answer play_arrow
question_answer 134) The perimeter of a certain sector of a circle is equal to the length of the arc of the semicircle. Then, the angle at the centre of the sector in radians is
A)
\[\pi -2\]
done
clear
B)
\[\pi +2\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{2\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 135) The value of \[\tan \,67\frac{{{1}^{o}}}{2}+\cos 67\frac{{{1}^{o}}}{2}\] is
A)
\[\sqrt{2}\]
done
clear
B)
\[3\sqrt{2}\]
done
clear
C)
\[2\sqrt{2}\]
done
clear
D)
\[2-\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 136) If \[f(x)\] is an even function and \[f'(x)\] exists, then \[f'(e)+f'(-e)\]is
A)
\[>0\]
done
clear
B)
\[0\]
done
clear
C)
\[\ge 0\]
done
clear
D)
\[<0\]
done
clear
View Answer play_arrow
question_answer 137) If a is a complex number satisfying the equation \[{{a}^{2}}+a+1=0,\]then \[{{\alpha }^{31}}\]is equal to
A)
\[\alpha \]
done
clear
B)
\[{{\alpha }^{2}}\]
done
clear
C)
\[1\]
done
clear
D)
\[i\]
done
clear
View Answer play_arrow
question_answer 138) The derivative of \[\sin ({{x}^{3}})\] w.r.t. \[cos({{x}^{3}})\] is
A)
\[-\tan ({{x}^{3}})\]
done
clear
B)
\[\tan ({{x}^{3}})\]
done
clear
C)
\[-cot({{x}^{3}})\]
done
clear
D)
\[cot({{x}^{3}})\]
done
clear
View Answer play_arrow
question_answer 139) A unit vector perpendicular to both the vectors \[\hat{i}+\hat{j}\]and \[\hat{j}+\hat{k}\]
A)
\[\frac{-\hat{i}-\hat{j}+\hat{k}}{\sqrt{3}}\]
done
clear
B)
\[\frac{\hat{i}+\hat{j}-\hat{k}}{3}\]
done
clear
C)
\[\frac{\hat{i}+\hat{j}+\hat{k}}{\sqrt{3}}\]
done
clear
D)
\[\frac{\hat{i}-\hat{j}+\hat{k}}{\sqrt{3}}\]
done
clear
View Answer play_arrow
question_answer 140) If \[A=\left| \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\ \end{matrix} \right|\] and \[B=\left| \begin{matrix} {{c}_{1}} & {{c}_{2}} & {{c}_{3}} \\ {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ \end{matrix} \right|,\] then
A)
\[A=-B\]
done
clear
B)
\[A=B\]
done
clear
C)
\[B=0\]
done
clear
D)
\[B={{A}^{2}}\]
done
clear
View Answer play_arrow
question_answer 141) On the set Z of all integers * is defined by \[a*b=a+b-5,\] if \[2*(x*3)=5,\]then x is equal to
A)
\[0\]
done
clear
B)
\[3\]
done
clear
C)
\[5\]
done
clear
D)
\[10\]
done
clear
View Answer play_arrow
question_answer 142) Which of the following is false?
A)
Addition is commutative in N
done
clear
B)
Multiplication is associative in N
done
clear
C)
If \[a*b={{a}^{b}}\] for all a, \[b\in N\] then * is commutative in N
done
clear
D)
Addition is associative in N
done
clear
View Answer play_arrow
question_answer 143) If \[\vec{a}.\hat{i}=\vec{a}.\left( \hat{i}+\hat{j} \right)=\vec{a}.\left( \hat{i}+\hat{j}+\hat{k} \right)=1\] then \[\vec{a}\] is equal to
A)
\[\hat{i}+\hat{j}\]
done
clear
B)
\[\hat{i}-\hat{k}\]
done
clear
C)
\[\hat{i}\]
done
clear
D)
\[\hat{i}+\hat{j}-\hat{k}\]
done
clear
View Answer play_arrow
question_answer 144) If a and b are unit vectors and \[|\vec{a}+\vec{b}|=1,\] then\[|\vec{a}-\vec{b}|=1,\] is equal to
A)
\[\sqrt{2}\]
done
clear
B)
\[1\]
done
clear
C)
\[\sqrt{5}\]
done
clear
D)
\[\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 145) The projection of \[\vec{a}=3\hat{i}-\hat{j}+5\hat{k}\] on \[\vec{b}=2\hat{i}+3\hat{j}+\hat{k}\]is
A)
\[\frac{8}{\sqrt{35}}\]
done
clear
B)
\[\frac{8}{\sqrt{39}}\]
done
clear
C)
\[\frac{8}{\sqrt{14}}\]
done
clear
D)
\[\sqrt{14}\]
done
clear
View Answer play_arrow
question_answer 146) If \[A\left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix} \right],\]then \[{{A}^{-1}}\] is equal to
A)
\[-\frac{1}{2}\left[ \begin{matrix} 4 & -2 \\ -3 & 1 \\ \end{matrix} \right]\]
done
clear
B)
\[\frac{1}{2}\left[ \begin{matrix} 4 & -2 \\ -3 & 1 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} -2 & 4 \\ 1 & 3 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 2 & 4 \\ 1 & 3 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 147) The set \[\{-1,0,1\}\] is not a multiplicative group because of the failure of
A)
closure law
done
clear
B)
associative law
done
clear
C)
identity law
done
clear
D)
inverse law
done
clear
View Answer play_arrow
question_answer 148) The angle of elevation of the top of a TV tower from three points A, B and C in a straight line through the foot of the tower are \[\alpha ,2\alpha \] and \[3\alpha \]respectively. If \[AB=a,\] then height of the tower is
A)
\[a\text{ }tan\text{ }\alpha \]
done
clear
B)
\[a\text{ }sin\text{ }\alpha \]
done
clear
C)
\[a\text{ }sin\text{ 2}\alpha \]
done
clear
D)
\[a\text{ }sin\text{ 3}\alpha \]
done
clear
View Answer play_arrow
question_answer 149) The angles A, B and C of a triangle ABC are in AP. If \[b:c=\sqrt{3}:\sqrt{2},\] then the angle A is
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{15}^{o}}\]
done
clear
C)
\[{{75}^{o}}\]
done
clear
D)
\[{{45}^{o}}\]
done
clear
View Answer play_arrow
question_answer 150) \[\sin \left( 2{{\sin }^{-1}}\sqrt{\frac{63}{65}} \right)\] is equal to
A)
\[\frac{2\sqrt{126}}{65}\]
done
clear
B)
\[\frac{4\sqrt{65}}{65}\]
done
clear
C)
\[\frac{8\sqrt{63}}{65}\]
done
clear
D)
\[\frac{\sqrt{63}}{65}\]
done
clear
View Answer play_arrow
question_answer 151) A variable line \[\frac{x}{a}+\frac{y}{b}=1\] is such that \[a+b=4\] The locus of the mid point of the portion of the line intercepted between the axes is
A)
\[x+y=4\]
done
clear
B)
\[x+y=8\]
done
clear
C)
\[x+y=1\]
done
clear
D)
\[x+y=2\]
done
clear
View Answer play_arrow
question_answer 152) The point \[(5,-7)\] lies outside the circle
A)
\[{{x}^{2}}+{{y}^{2}}-8x=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-5x+7y=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-5x+7y-1=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-8x+7y-2=0\]
done
clear
View Answer play_arrow
question_answer 153) If the circles \[{{x}^{2}}+{{y}^{2}}=9\]and \[{{x}^{2}}+{{y}^{2}}+2\alpha x+2y+1=0\]touch each other internally, then a is equal to
A)
\[\pm \frac{4}{3}\]
done
clear
B)
\[1\]
done
clear
C)
\[\frac{4}{3}\]
done
clear
D)
\[-\frac{4}{3}\]
done
clear
View Answer play_arrow
question_answer 154) The locus of the mid point of the line joining the focus and any point on the parabola \[{{y}^{2}}=4ax\] is a parabola with the equation of directrix as
A)
\[x+a=0\]
done
clear
B)
\[2x+a=0\]
done
clear
C)
\[x=0\]
done
clear
D)
\[x=\frac{a}{2}\]
done
clear
View Answer play_arrow
question_answer 155) The tangents drawn at the extremities of a focal chord of the parabola \[{{y}^{2}}=16x\]
A)
intersect on \[x=0\]
done
clear
B)
intersect on the line \[x+4=0\]
done
clear
C)
intersect at an angle of \[{{60}^{o}}\]
done
clear
D)
intersect at an angle of \[{{45}^{o}}\]
done
clear
View Answer play_arrow
question_answer 156) If \[f:R\to R\] is defined by \[f(x)={{x}^{3}},\] then \[{{f}^{-1}}(8)\]is equal to
A)
\[\{2\}\]
done
clear
B)
\[\{2,2\omega ,2{{\omega }^{2}}\}\]
done
clear
C)
\[\{2,-2\}\]
done
clear
D)
\[\{2,2\}\]
done
clear
View Answer play_arrow
question_answer 157) R is a relation on. N given by \[R=\{(x,y):4x+3y=20\}\]. Which of the following belongs to R?
A)
\[(-4,12)\]
done
clear
B)
\[(5,0)\]
done
clear
C)
\[(3,4)\]
done
clear
D)
\[(2,4)\]
done
clear
View Answer play_arrow
question_answer 158) If \[{{\log }_{10}}7=0.8451,\]then the position of the first significant figure of \[{{7}^{-20}}\]is
A)
\[16\]
done
clear
B)
\[17\]
done
clear
C)
\[20\]
done
clear
D)
\[15\]
done
clear
View Answer play_arrow
question_answer 159) \[\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+.....\]upto n terms is equal to
A)
\[\frac{n}{4n+6}\]
done
clear
B)
\[\frac{1}{6n+4}\]
done
clear
C)
\[\frac{n}{6n+4}\]
done
clear
D)
\[\frac{n}{3n+7}\]
done
clear
View Answer play_arrow
question_answer 160) The ten's digit in \[1!4!+7!+10!+12!+13!+15!+16!+17!\]is divisible by
A)
\[4\]
done
clear
B)
\[3!\]
done
clear
C)
\[5\]
done
clear
D)
\[7\]
done
clear
View Answer play_arrow
question_answer 161) The value of \[\int_{-2}^{2}{(a{{x}^{3}}+bx+c)}dx\] depends on the
A)
value of b
done
clear
B)
value of c
done
clear
C)
value of a
done
clear
D)
values of a and b
done
clear
View Answer play_arrow
question_answer 162) The area of the region bounded by \[y=2x-{{x}^{2}}\]and the x -axis is
A)
\[\frac{8}{3}sq\,unit\]
done
clear
B)
\[\frac{4}{3}sq\,unit\]
done
clear
C)
\[\frac{7}{3}sq\,unit\]
done
clear
D)
\[\frac{2}{3}sq\,unit\]
done
clear
View Answer play_arrow
question_answer 163) The differential equation \[y\,\frac{dy}{dx}+x=\]represents
A)
a family of hyperbolas
done
clear
B)
a family of circles whose centres are on the y-axis
done
clear
C)
a family of parabolas
done
clear
D)
a family of circles whose centres are on the x-axis
done
clear
View Answer play_arrow
question_answer 164) If \[f({{x}^{5}})=5{{x}^{3}},\]then \[f'(x)\] is equal to
A)
\[\frac{3}{\sqrt[5]{{{x}^{2}}}}\]
done
clear
B)
\[\frac{3}{\sqrt[5]{x}}\]
done
clear
C)
\[\frac{3}{x}\]
done
clear
D)
\[\sqrt[5]{x}\]
done
clear
View Answer play_arrow
question_answer 165) \[f(x)=\left\{ \begin{matrix} 2a-x & in & -a<x<a \\ 3x-2a & in & a\le x \\ \end{matrix} \right.\] Then, which of the following is true?
A)
\[f(x)\] is discontinuous at \[x=a\]
done
clear
B)
\[f(x)\] is not differentiable at \[x=a\]
done
clear
C)
\[f(x)\] is differentiable at \[x\ge a\]
done
clear
D)
\[f(x)\] is continuous at all \[x<a\]
done
clear
View Answer play_arrow
question_answer 166) The maximum area of a rectangle that can be inscribed in a circle of radius 2 unit is (in square unit)
A)
\[4\]
done
clear
B)
\[8\pi \]
done
clear
C)
\[8\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow
question_answer 167) If z is a complex number such that \[z=-\bar{z},\] then
A)
z is purely real
done
clear
B)
z is purely imaginary
done
clear
C)
z is any complex number
done
clear
D)
real part of z is the same as its imaginary part
done
clear
View Answer play_arrow
question_answer 168) The value of \[\underset{k=1}{\mathop{\overset{6}{\mathop{\Sigma }}\,}}\,\left( \sin \frac{2k\pi }{7}-i\cos \frac{2k\pi }{7} \right)\]is
A)
\[i\]
done
clear
B)
\[0\]
done
clear
C)
\[-i\]
done
clear
D)
\[-1\]
done
clear
View Answer play_arrow
question_answer 169) \[\underset{x\to \infty }{\mathop{\lim }}\,\,x\,\sin \left( \frac{2}{x} \right)\] is equal to
A)
\[\infty \]
done
clear
B)
\[0\]
done
clear
C)
\[2\]
done
clear
D)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 170) A stone is thrown vertically upwards and the height x ft reached by the stone in t seconds is given by\[x=80t-16{{t}^{2}}\]. The stone reaches the maximum height in
A)
\[2s\]
done
clear
B)
\[2.5s\]
done
clear
C)
\[3s\]
done
clear
D)
\[1.5s\]
done
clear
View Answer play_arrow
question_answer 171) The maximum value of \[\frac{\log x}{x}\] in \[(2,\infty )\] is
A)
\[1\]
done
clear
B)
\[\frac{2}{e}\]
done
clear
C)
\[e\]
done
clear
D)
\[\frac{1}{e}\]
done
clear
View Answer play_arrow
question_answer 172) If \[f(x)=b{{e}^{ax}}+a{{e}^{bx}},\] then \[f'(0)\] is equal to
A)
\[0\]
done
clear
B)
\[2ab\]
done
clear
C)
\[ab(a+b)\]
done
clear
D)
\[ab\]
done
clear
View Answer play_arrow
question_answer 173) If \[\sqrt{\frac{1+\cos A}{1-csoA}}=\frac{x}{y},\] then the value of tan A is is equal is
A)
\[\frac{{{x}^{2}}+{{y}^{2}}}{{{x}^{2}}-{{y}^{2}}}\]
done
clear
B)
\[\frac{2xy}{{{x}^{2}}+{{y}^{2}}}\]
done
clear
C)
\[\frac{{{x}^{2}}+{{y}^{2}}}{{{x}^{2}}-{{y}^{2}}}\]
done
clear
D)
\[\frac{2xy}{{{y}^{2}}-{{x}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 174) \[\int{\frac{\sec \,x}{\sec \,x+\tan x}}dx\]is equal to
A)
\[\tan \,x-\sec x+C\]
done
clear
B)
\[\log (1+\sec x)+C\]
done
clear
C)
\[\sec x+\tan \,x+C\]
done
clear
D)
\[\log \sin x+\log \cos x+C\]
done
clear
View Answer play_arrow
question_answer 175) If \[\int{f(x)\,dx=g(x),}\] then \[\int{f(x)\,g=g(x)\,dx}\] is equal to
A)
\[\frac{1}{2}{{f}^{2}}(x)\]
done
clear
B)
\[\frac{1}{2}{{g}^{2}}(x)\]
done
clear
C)
\[\frac{1}{2}{{[g'(x)]}^{2}}\]
done
clear
D)
\[f'(x)g(x)\]
done
clear
View Answer play_arrow
question_answer 176) The general solution of \[|\sin x|=\cos x\]is (when\[n\,\in \,I\]) given by
A)
\[n\pi +\frac{\pi }{4}\]
done
clear
B)
\[2n\,\,\pi \pm \frac{\pi }{4}\]
done
clear
C)
\[n\,\,\pi \pm \frac{\pi }{4}\]
done
clear
D)
\[n\,\,\pi -\frac{\pi }{4}\]
done
clear
View Answer play_arrow
question_answer 177) The real root of the equation \[{{x}^{3}}-6x+9=0\] is
A)
\[-6\]
done
clear
B)
\[-9\]
done
clear
C)
\[6\]
done
clear
D)
\[-3\]
done
clear
View Answer play_arrow
question_answer 178) The digit in the unit?s place of \[{{5}^{834}}\] is
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[3\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow
question_answer 179) The remainder when \[{{3}^{100}}\times {{2}^{50}}\]is divided by 5 is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 180) \[\int{\frac{\sin x\,\cos x}{\sqrt{1-{{\sin }^{4}}x}}}dx\] is equal to
A)
\[\frac{1}{2}{{\sin }^{-1}}({{\sin }^{2}}x)+C\]
done
clear
B)
\[\frac{1}{2}{{\cos }^{-1}}({{\sin }^{2}}x)+C\]
done
clear
C)
\[{{\tan }^{-1}}({{\sin }^{2}}x)+C\]
done
clear
D)
\[{{\tan }^{-1}}(2{{\sin }^{2}}x)+C\]
done
clear
View Answer play_arrow