question_answer 1) A boat carrying a number of large stones is floating in a water tank. What would happen to the water level, if a few stones are unloaded into water?
A)
Rises
done
clear
B)
Falls
done
clear
C)
Remains unchanged
done
clear
D)
Rises till half the number of stones are unloaded and then begins to fall
done
clear
View Answer play_arrow
question_answer 2) A container with square base of side a is filled up to a height H with a liquid. A hole is made at a depth h from the free surface of water. With what acceleration the container must be accelerated, so that the water does not come out?
A)
\[g\]
done
clear
B)
\[\frac{g}{2}\]
done
clear
C)
\[\frac{2gH}{2}\]
done
clear
D)
\[\frac{2gh}{2}\]
done
clear
View Answer play_arrow
question_answer 3) If two soap bubbles of equal radii r coalesce, then the radius of curvature of interface between two bubbles will be
A)
r
done
clear
B)
zero
done
clear
C)
infinity
done
clear
D)
\[\frac{1}{2r}\]
done
clear
View Answer play_arrow
question_answer 4) What is the mass of \[2\text{ }L\]of nitrogen at \[~22.4\text{ }arm\]pressure and \[273\text{ }K\]?
A)
\[28\text{ }g\]
done
clear
B)
\[14\times 22.4\text{ }g\]
done
clear
C)
\[56\text{ }g\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 5) \[2\text{ }g\]of water condenses when passed through \[40\text{ }g\]of water initially at\[{{25}^{o}}C\]. The- condensation of steam raises the temperature of water to \[{{54.3}^{o}}C\]. What is the latent heat of steam?
A)
\[540\,\,cal/g\]
done
clear
B)
\[536\,\,cal/g\]
done
clear
C)
\[270\,\,cal/g\]
done
clear
D)
\[480\,\,cal/g\]
done
clear
View Answer play_arrow
question_answer 6) Petrol engine does the work during
A)
suction stroke
done
clear
B)
exhaust stroke
done
clear
C)
adiabatic expansion
done
clear
D)
combustion
done
clear
View Answer play_arrow
question_answer 7) The spectral energy distribution of a star is maximum at twice temperature as that of sun. The total energy radiated by star is
A)
twice as that of the sun
done
clear
B)
same as that of the sun
done
clear
C)
sixteen times as that of the sun
done
clear
D)
one-sixteenth of sun
done
clear
View Answer play_arrow
question_answer 8) Two simple pendulums of lengths \[1.44\text{ }m\]and \[1\text{ }m\] start swinging together. After how many vibrations will they again start swinging together?
A)
5 oscillations of smaller pendulum
done
clear
B)
6 oscillations of smaller pendulum
done
clear
C)
4 oscillations of bigger pendulum
done
clear
D)
6 oscillations of bigger pendulum
done
clear
View Answer play_arrow
question_answer 9) A wave has velocity u in medium P and velocity \[2u\] in medium Q. If the wave is incident in medium P at an angle \[{{30}^{o}},\]then the angle of refraction will be
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{45}^{o}}\]
done
clear
C)
\[{{60}^{o}}\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 10) In \[1\text{ }m\]long open pipe what is the harmonic of resonance obtained with a tuning fork of frequency \[480\text{ }Hz\]?
A)
First
done
clear
B)
Second
done
clear
C)
Third
done
clear
D)
Fourth
done
clear
View Answer play_arrow
question_answer 11) Three sources of equal intensities with frequencies 400,401 and 402 vib/s are sounded together. The number of beat/s is
A)
zero
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 12) Two pendulums begin to swing simultaneously. If the ratio of the frequency of oscillations of the two is \[7:8,\] then the ratio of lengths of the two pendulums will be
A)
\[7:8\]
done
clear
B)
\[8:7\]
done
clear
C)
\[49:64\]
done
clear
D)
\[64:49\]
done
clear
View Answer play_arrow
question_answer 13) In a resonance pipe the first and second resonances are obtained at depths \[22.7\text{ }cm\]and \[70.2\text{ }cm\]respectively. What will be the end correction?
A)
\[1.05\,\,cm\]
done
clear
B)
\[115.5\,\,cm\]
done
clear
C)
\[92.5\,\,cm\]
done
clear
D)
\[113.5\,\,cm\]
done
clear
View Answer play_arrow
question_answer 14) The intensity level of sound A is 30 dB greater than of B. How many times more intense is the sound A than B?
A)
\[10\]
done
clear
B)
\[100\]
done
clear
C)
\[1000\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 15) An open tube is in resonance with string. If tube is dipped in water, so that \[75%\]of length of tube is inside water, then the ratio of the frequency \[({{v}_{o}})\] of tube to string is
A)
\[{{v}_{o}}\]
done
clear
B)
\[2{{v}_{o}}\]
done
clear
C)
\[\frac{2}{3}{{v}_{o}}\]
done
clear
D)
\[\frac{3}{2}{{v}_{o}}\]
done
clear
View Answer play_arrow
question_answer 16)
Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are suspended together by a massless spring of constant k. When the masses are in equilibrium \[{{m}_{1}},\] is removed without disturbing the system. The amplitude of oscillations is
A)
\[\frac{{{m}_{1}}g}{k}\]
done
clear
B)
\[\frac{{{m}_{2}}g}{k}\]
done
clear
C)
\[\frac{({{m}_{1}}+{{m}_{2}})g}{k}\]
done
clear
D)
\[\frac{({{m}_{1}}-{{m}_{2}})g}{k}\]
done
clear
View Answer play_arrow
question_answer 17) If a conducting medium is placed between two charges, then the electric force between will become
A)
zero
done
clear
B)
infinity
done
clear
C)
\[1N\]
done
clear
D)
1 dyne
done
clear
View Answer play_arrow
question_answer 18) If an electron moves from rest from a point at which potential is \[50\text{ }V\]to another point at which potential is \[70\text{ }V,\] then its kinetic energy in the final state will be
A)
\[3.2\times {{10}^{-20}}J~\]
done
clear
B)
\[3.2\times {{10}^{-18}}J\]
done
clear
C)
\[3.2\times {{10}^{-19}}J\]
done
clear
D)
zero
done
clear
View Answer play_arrow
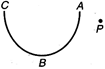
question_answer 19)
In the following diagram the work done in moving a point charge from point P to point A, B and C is respectively as \[{{W}_{A}},\] \[{{W}_{B}}\] and \[{{W}_{C}},\] then
A)
\[{{W}_{A}}={{W}_{B}}={{W}_{C}}\]
done
clear
B)
\[{{W}_{A}}={{W}_{B}}={{W}_{C}}=0\]
done
clear
C)
\[{{W}_{A}}>{{W}_{B}}>{{W}_{C}}\]
done
clear
D)
\[{{W}_{A}}<{{W}_{B}}<{{W}_{C}}\]
done
clear
View Answer play_arrow
question_answer 20) The electric field due to an electric dipole at a distance r from its centre in axial position is E. If the dipole is rotated through an angle of \[{{90}^{o}}\]about its perpendicular axis, the electric field at the same point will be
A)
\[E\]
done
clear
B)
\[\frac{E}{4}\]
done
clear
C)
\[\frac{E}{2}\]
done
clear
D)
\[2E\]
done
clear
View Answer play_arrow
question_answer 21) If eight similar charge drops combine to form a bigger drop, then the ratio of capacitance of bigger drop to that of smaller drop will be
A)
\[2:1\]
done
clear
B)
\[8:1\]
done
clear
C)
\[4:1\]
done
clear
D)
\[16:1\]
done
clear
View Answer play_arrow
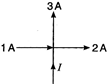
question_answer 22)
The value of current I in figure is
A)
\[4\,A\]
done
clear
B)
\[6\,A\]
done
clear
C)
\[3\,A\]
done
clear
D)
\[5\,A\]
done
clear
View Answer play_arrow
question_answer 23) The plates of a charged condenser are connected to a voltmeter. If the plates are moved apart, the reading of voltmeter will
A)
increase
done
clear
B)
decrease
done
clear
C)
remain unchanged
done
clear
D)
information is insufficient
done
clear
View Answer play_arrow
question_answer 24) The n rows each containing m cells in series are joined in parallel. Maximum current is taken from this combination across an external resistance of 30 resistance. If the total number of cells used are 24 and internal resistance of each cell is \[0.5\text{ }Q\]then
A)
\[m=8,\text{ }n=3\]
done
clear
B)
\[m=6,\text{ }n=4\]
done
clear
C)
\[m=12,\text{ }n=2\]
done
clear
D)
\[m=2,\text{ }n=12\]
done
clear
View Answer play_arrow
question_answer 25) A railway compartment is lit up by thirteen lamps each taking \[2.1\text{ }A\]at\[15\text{ }V\]. The heat generated per second in each lamp will be m
A)
\[4.35\text{ }cal\]
done
clear
B)
\[5.73\text{ }cal\]
done
clear
C)
\[7.5\text{ }cal\]
done
clear
D)
\[2.5\text{ }cal\]
done
clear
View Answer play_arrow
question_answer 26) The chemical equivalent of copper and zinc are 32 and 108 respectively. When copper and silver voltameter are connected in series and electric current is passed through for sometimes, \[1.6\text{ }g\]of copper is deposited. Then, the mass of silver deposited will be
A)
\[3.5\text{ }g\]
done
clear
B)
\[2.8g\]
done
clear
C)
\[5.4\text{ }g\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 27) If the emf of a thermocouple, one junction of which is kept \[0{}^\circ C\]is given by \[e=at+\frac{1}{2}b{{t}^{2}}\] then the neutral temperature will be
A)
\[\frac{a}{b}\]
done
clear
B)
\[-\frac{a}{b}\]
done
clear
C)
\[\frac{a}{2b}\]
done
clear
D)
\[-\frac{1}{ab}\]
done
clear
View Answer play_arrow
question_answer 28) The direction of magnetic lines of force produced by passing a direct current in a conductor is given by
A)
Lenz'slaw
done
clear
B)
Fleming's left hand rule
done
clear
C)
Right hand palm rule
done
clear
D)
Maxwell's law
done
clear
View Answer play_arrow
question_answer 29) A proton, a deuteron and an alpha particle are accelerated through same potential difference and then they enter a normal uniform magnetic field. The ratio of their kinetic energies will be
A)
\[2:1:3\]
done
clear
B)
\[1:1:2\]
done
clear
C)
\[1:1:1\]
done
clear
D)
\[1:2:4\]
done
clear
View Answer play_arrow
question_answer 30) For the magnetic field to be maximum due to a small element of current carrying conductor at a point, the angle between the element and the line joining the element to the given point must be
A)
\[{{0}^{o}}\]
done
clear
B)
\[{{90}^{o}}\]
done
clear
C)
\[{{180}^{o}}\]
done
clear
D)
\[{{45}^{o}}\]
done
clear
View Answer play_arrow
question_answer 31) A circular coil of 20 turns and radius 10 cm is placed in uniform magnetic field of \[0.10\text{ }T\]normal to the plane of the coil. If the current in coil is 5 A, then the torque acting on the coil will be
A)
\[31.4\text{ }Nm\]
done
clear
B)
\[3.14\text{ }Nm\]
done
clear
C)
\[0.314\text{ }Nm\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 32) The earth's magnetic field inside an iron box as compared to that outside the box is
A)
less
done
clear
B)
more
done
clear
C)
zero
done
clear
D)
same
done
clear
View Answer play_arrow
question_answer 33) The intensity of magnetic field due to an isolated pole of strength m at a point distant r from it will be
A)
\[\frac{m}{{{r}^{2}}}\]
done
clear
B)
\[m{{r}^{2}}\]
done
clear
C)
\[\frac{{{r}^{2}}}{m}\]
done
clear
D)
\[\frac{m}{r}\]
done
clear
View Answer play_arrow
question_answer 34) The dimensions of self-inductance L are
A)
\[[M{{L}^{2}}{{T}^{-2}}{{A}^{-2}}]\]
done
clear
B)
\[[M{{L}^{2}}{{T}^{-1}}{{A}^{-2}}]\]
done
clear
C)
\[[M{{L}^{2}}{{T}^{-1}}{{A}^{-1}}]\]
done
clear
D)
\[[M{{L}^{-2}}{{T}^{-2}}{{A}^{-2}}]\]
done
clear
View Answer play_arrow
question_answer 35) Quantity that remains unchanged in a transformer is
A)
voltage
done
clear
B)
current
done
clear
C)
frequency
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 36) If the capacity of a condenser is 1 F, then its resistance in a DC circuit will be
A)
zero
done
clear
B)
infinity
done
clear
C)
\[1\Omega \]
done
clear
D)
\[\frac{1}{2}\,\,\Omega \]
done
clear
View Answer play_arrow
question_answer 37) The time taken by an alternating current of \[50\text{ }Hz\] in reaching from zero to its maximum value will be
A)
\[0.5s\]
done
clear
B)
\[0.005s\]
done
clear
C)
\[0.05\text{ }s\]
done
clear
D)
\[5s\]
done
clear
View Answer play_arrow
question_answer 38) If the area to be covered for TV telecast is doubled, then height of transmitting antenna (TV tower) will have to be
A)
doubled
done
clear
B)
halved
done
clear
C)
quadrupled
done
clear
D)
kept unchanged
done
clear
View Answer play_arrow
question_answer 39) An electromagnetic radiation has an energy \[14.4\text{ }eV\]. To which region of electromagnetic spectrum does it belong?
A)
Ultraviolet region
done
clear
B)
Visible region
done
clear
C)
X-ray region
done
clear
D)
y-ray region
done
clear
View Answer play_arrow
question_answer 40) When a ray of light is incident normally on a surface, then
A)
total internal reflection takes place
done
clear
B)
it passes undeviated
done
clear
C)
it undergoes dispersion
done
clear
D)
it gets absorbed by the surface
done
clear
View Answer play_arrow
question_answer 41) A ray of light passes through a glass plate of thickness t and refractive index u. If the speed of light in vacuum is c, then the time taken by light in passing through the plate will be
A)
\[\mu t\]
done
clear
B)
\[\frac{\mu t}{c}\]
done
clear
C)
\[\frac{tc}{\mu }\]
done
clear
D)
\[\frac{t}{\mu c}\]
done
clear
View Answer play_arrow
question_answer 42) In Young's double slit experiment with monochromatic light, the central fringe will be
A)
coloured
done
clear
B)
white
done
clear
C)
bright
done
clear
D)
black
done
clear
View Answer play_arrow
question_answer 43) In the phenomenon of interference, energy is
A)
destroyed at bright'fringes
done
clear
B)
created at dark fringes
done
clear
C)
conserved but it is redistributed
done
clear
D)
same at all points
done
clear
View Answer play_arrow
question_answer 44) A very thin film that reflects white light appears
A)
coloured
done
clear
B)
white
done
clear
C)
black
done
clear
D)
red
done
clear
View Answer play_arrow
question_answer 45) The size of an obstacle in order to observe diffraction of light must be
A)
of any order
done
clear
B)
of the order of wavelength
done
clear
C)
much larger than wavelength
done
clear
D)
much smaller than wavelength
done
clear
View Answer play_arrow
question_answer 46) If the binding energies of a deuteron and an alpha-particle are \[1.125\text{ }MeV\]and \[7.2\text{ }MeV,\] respectively, then the more stable of the two is
A)
deuteron
done
clear
B)
alpha-particle
done
clear
C)
both [a] and [b]
done
clear
D)
sometimes deuteron and sometimes alpha particle
done
clear
View Answer play_arrow
question_answer 47) The particle A is converted into C via following reaction, \[A\xrightarrow{{}}B{{+}_{2}}H{{e}^{4}}\] \[B\xrightarrow{{}}C+2{{e}^{-}}\] Then
A)
A and C are isobars
done
clear
B)
A and C are isotopes
done
clear
C)
A and B are isobars
done
clear
D)
A and B are isotopes
done
clear
View Answer play_arrow
question_answer 48) On bombardment of \[{{U}^{235}}\] by slow neutrons, 200 MeV energy is released. If the power output of atomic reactor is \[1.6\text{ }MW,\] then the rate of fission will be
A)
\[5\times {{10}^{16}}/s\]
done
clear
B)
\[10\times {{10}^{16}}/s\]
done
clear
C)
\[15\times {{10}^{16}}/s\]
done
clear
D)
\[20\times {{10}^{16}}/s\]
done
clear
View Answer play_arrow
question_answer 49) The fussion process is possible at high temperatures, because at higher temperatures
A)
the nucleus disintegrates
done
clear
B)
the molecules disintegrates
done
clear
C)
atoms become ionized
done
clear
D)
the nucleus get sufficient energy to overcome the strong forces of repulsion
done
clear
View Answer play_arrow
question_answer 50) For maintaining sustained chain reaction, the following is required
A)
protons
done
clear
B)
electrons
done
clear
C)
neutrons
done
clear
D)
positrons
done
clear
View Answer play_arrow
question_answer 51) Sun maintains its shining because of the
A)
fission of helium
done
clear
B)
chemical reaction
done
clear
C)
fusion of hydrogen nuclei
done
clear
D)
burning of carbon
done
clear
View Answer play_arrow
question_answer 52) Atomic reactor is based on
A)
controlled chain reaction
done
clear
B)
uncontrolled chain reaction
done
clear
C)
nuclear fission
done
clear
D)
nuclear fussion
done
clear
View Answer play_arrow
question_answer 53) If the frequency of light incident on metal surface is doubled, then kinetic energy of emitted electron will become
A)
doubled
done
clear
B)
less than double
done
clear
C)
more than double
done
clear
D)
nothing can be said
done
clear
View Answer play_arrow
question_answer 54) The energy gap of silicon is \[1.14\text{ }eV\]. At what wavelength the silicon will stop to absorb the photon?
A)
\[10877\text{ }\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[\text{9888 }\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[1087.7\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[1000\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 55) n-p-n transistor are preferred to p-n-p transistor because they have
A)
low cost
done
clear
B)
low dissipation energy
done
clear
C)
capability of handling large power
done
clear
D)
electrons having high mobility than holes
done
clear
View Answer play_arrow
question_answer 56) In a transistor in common-emitter configuration, the ratio of power gain to voltage gain is
A)
\[\alpha \]
done
clear
B)
\[\frac{\beta }{\alpha }\]
done
clear
C)
\[\beta \times \beta \]
done
clear
D)
\[\beta \]
done
clear
View Answer play_arrow
question_answer 57) The ionic bond is absent in
A)
\[NaCl\]
done
clear
B)
\[CsCl\]
done
clear
C)
\[LiF\]
done
clear
D)
\[{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 58) As the temperature rises the resistance offered by metal
A)
increases
done
clear
B)
decreases
done
clear
C)
remains same
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 59) Density of liquid in CGS system is \[0.625\text{ }g/c{{m}^{3}}\] What is its magnitude in SI system?
A)
\[0.625\]
done
clear
B)
\[0.0625\]
done
clear
C)
\[0.00625\]
done
clear
D)
\[625\]
done
clear
View Answer play_arrow
question_answer 60) If the length of rod A is \[3.25\pm 0.01\,cm\]and that of B is \[4.19\pm 0.01\text{ }cm,\] then the rod B is longer than rod A by
A)
\[0.94\pm 0.00\text{ }cm\]
done
clear
B)
\[0.94\pm 0.01\text{ }cm\]
done
clear
C)
\[0.94\pm 0.02\text{ }cm\]
done
clear
D)
\[0.94\pm 0.005\text{ }cm\]
done
clear
View Answer play_arrow
question_answer 61) A man is \[45\text{ }m\]behind the bus, when the bus start accelerating from rest with-acceleration \[2.5m/{{s}^{2}}\]. With what minimum velocity should the man start running to catch the bus?
A)
\[12\text{ }m/s\]
done
clear
B)
\[14\text{ }m/s\]
done
clear
C)
\[15\text{ }m/s\]
done
clear
D)
\[16\text{ }m/s\]
done
clear
View Answer play_arrow
question_answer 62) A particle moves along x-axis as \[x=4\,(t-2)+a{{(t-2)}^{2}}\] Which of the flowing is true?
A)
The initial velocity of particle is 4
done
clear
B)
The acceleration of particle is \[2a\]
done
clear
C)
The particle is at origin at \[t=0\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 63) The momentum of the particle at any instant is given by \[3\,\cos 4t\,\hat{i}+3\,\sin \,4t\,\hat{j}\]. What is the angle between momentum and force-acting on it?
A)
\[{{60}^{o}}\]
done
clear
B)
\[{{30}^{o}}\]
done
clear
C)
\[{{45}^{o}}\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 64) A boat moves with a speed of \[5\text{ }km/h\]relative to water in a river flowing with a speed of \[3\text{ }km/h\]and having a width of\[1\text{ }km\]. The time taken around a round trip is
A)
\[5\text{ }min\]
done
clear
B)
\[60\text{ }min\]
done
clear
C)
\[20\text{ }min\]
done
clear
D)
\[30\text{ }min\]
done
clear
View Answer play_arrow
question_answer 65) A man is standing at the centre of frictionless pond of ice. How can he get himself to the shore?
A)
By throwing his shirt in vertically upward direction
done
clear
B)
By spitting horizontally
done
clear
C)
He will wait for the ice to melt in pond
done
clear
D)
Unable to get at the shore
done
clear
View Answer play_arrow
question_answer 66) If the heart pushes \[1\text{ }cc\]of blood in 1 s under pressure \[20000\text{ }N{{m}^{2}},\]the power of heart is
A)
\[0.02\text{ }W\]
done
clear
B)
\[400\text{ }W\]
done
clear
C)
\[5\times {{10}^{-10}}W\]
done
clear
D)
\[0.2\text{ }W\]
done
clear
View Answer play_arrow
question_answer 67) A body of mass \[4\text{ }kg\]moving with velocity \[12\text{ }m/s\]collides with another body of mass \[\text{6 }kg\] at rest. If two, bodies stick together after collision, then the loss of kinetic energy of system is
A)
zero
done
clear
B)
\[288\text{ }J\]
done
clear
C)
\[172.8\text{ }J\]
done
clear
D)
\[144\text{ }J\]
done
clear
View Answer play_arrow
question_answer 68) A man does a given amount of work in \[10\text{ }s\]. Another man does the' same amount of work in \[20\text{ }s\]. The ratio of the output power of first man to the second man is
A)
\[1\]
done
clear
B)
\[1/2\]
done
clear
C)
\[2/1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 69) Turning effect is produced by
A)
tangential component of force
done
clear
B)
radial component of force
done
clear
C)
transverse component of force
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 70) For spheres each of mass M and radius R are placed with their centres on the four comers A, B, C and D of a square of side b. The spheres A and B are hollow and C and D are solids. The moment of inertia of the system about side AD of square is
A)
\[\frac{8}{3}M{{R}^{2}}+2M{{b}^{2}}\]
done
clear
B)
\[\frac{8}{5}M{{R}^{2}}+2M{{b}^{2}}\]
done
clear
C)
\[\frac{32}{15}M{{R}^{2}}+2M{{b}^{2}}\]
done
clear
D)
\[32M{{R}^{2}}+4M{{b}^{2}}\]
done
clear
View Answer play_arrow
question_answer 71) A particle describes a horizontal circle in a conical funnel whose inner surface is smooth with speed of \[0.5\text{ }m/s\]. What is the height of the plane of circle from vertex of the funnel?
A)
\[0.25\text{ }cm\]
done
clear
B)
\[2\text{ }cm\]
done
clear
C)
\[4\text{ }cm\]
done
clear
D)
\[2.5\text{ }cm\]
done
clear
View Answer play_arrow
question_answer 72) Two masses \[{{m}_{1}}\] and \[{{m}_{2}}({{m}_{1}}>{{m}_{2}})\]are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A)
\[{{\left( \frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right)}^{2}}g\]
done
clear
B)
\[\frac{{{m}_{1}}-{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}g\]
done
clear
C)
\[\frac{{{m}_{1}}+{{m}_{2}}}{{{m}_{1}}-{{m}_{2}}}g\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 73) A satellite moves in a circle around the earth. The radius of this circle is equal to one-half of the radius of the moon's orbit. The satellite completes one revolution is
A)
\[\frac{1}{2}\] lunar month
done
clear
B)
\[\frac{2}{3}\] lunar month
done
clear
C)
\[{{2}^{-3/2}}\] lunar month
done
clear
D)
\[{{2}^{3/2}}\] lunar month
done
clear
View Answer play_arrow
question_answer 74) Earth binds the atmosphere because of
A)
gravity
done
clear
B)
oxygen between earth and atmosphere
done
clear
C)
both and
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 75) A geostationary satellite is revolving around the earth. To make it escape from gravitational field of earth, its velocity must be increased
A)
\[100%\]
done
clear
B)
\[41.4%\]
done
clear
C)
\[50%\]
done
clear
D)
\[59.6%\]
done
clear
View Answer play_arrow
question_answer 76) Who used the quantum theory for the first time to explain the structure of atom?
A)
de-Broglie
done
clear
B)
Bohr
done
clear
C)
Heisenberg
done
clear
D)
Einstein
done
clear
View Answer play_arrow
question_answer 77) The boiling point of water decreases at high altitudes because
A)
the atmospheric pressure is low
done
clear
B)
the temperature is low
done
clear
C)
the atmospheric pressure is high
done
clear
D)
the temperature is high
done
clear
View Answer play_arrow
question_answer 78) In a solid lattice, the cation has left a lattice site and is located at interstitial position, the lattice defect is
A)
interstitial defect
done
clear
B)
vacancy defect
done
clear
C)
Frenkel defect
done
clear
D)
Schottky defect
done
clear
View Answer play_arrow
question_answer 79) The entropy of crystalline substances at absolute zero going by the third law of thermodynamics should be taken as
A)
100
done
clear
B)
50
done
clear
C)
zero
done
clear
D)
different for different substances
done
clear
View Answer play_arrow
question_answer 80) \[\Delta G\]for a spontaneous reaction is
A)
zero
done
clear
B)
negative
done
clear
C)
positive
done
clear
D)
could be positive or negative
done
clear
View Answer play_arrow
question_answer 81) The IUPAC name for \[C{{H}_{3}}CO-C{{H}_{3}}\]is
A)
dimethyl ketone
done
clear
B)
acetone
done
clear
C)
propanal
done
clear
D)
propanone
done
clear
View Answer play_arrow
question_answer 82) Which of the following is not an endothermic reaction?
A)
Dehydrogenation
done
clear
B)
Ethane to ethene
done
clear
C)
Combustion of propane
done
clear
D)
Change of chlorine molecule into chlorine atoms
done
clear
View Answer play_arrow
question_answer 83) A process in which the system does not exchange heat with the surroundings is known as
A)
isothermal
done
clear
B)
isobaric
done
clear
C)
isochoric
done
clear
D)
adiabatic
done
clear
View Answer play_arrow
question_answer 84) Which of the following is not a non-eletrolyte?
A)
Acetic acid
done
clear
B)
Glucose
done
clear
C)
Ethanol
done
clear
D)
Urea
done
clear
View Answer play_arrow
question_answer 85) The unit \[\text{oh}{{\text{m}}^{-1}}\]is used for
A)
molar conductivity
done
clear
B)
equivalent conductivity
done
clear
C)
specific conductivity
done
clear
D)
conductance
done
clear
View Answer play_arrow
question_answer 86) The tendency of an electrode to lose electrons is known as
A)
eletrode potential
done
clear
B)
reduction potential
done
clear
C)
oxidation potential
done
clear
D)
emf
done
clear
View Answer play_arrow
question_answer 87) For the feasibility of a redox reaction in a cell, the emf should be
A)
positive
done
clear
B)
fixed
done
clear
C)
zero
done
clear
D)
negative
done
clear
View Answer play_arrow
question_answer 88) If the rate reaction\[A\to B\]doubles on increasing the concentration of A by 4 times, the order of the reaction is
A)
2
done
clear
B)
1
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 89) Fog is a colloidal solution of
A)
solid in gas
done
clear
B)
liquid in gas
done
clear
C)
gas in liquid
done
clear
D)
gas in solid
done
clear
View Answer play_arrow
question_answer 90) Muddy water can be purified through coagulation by using
A)
common salt
done
clear
B)
alums
done
clear
C)
sand
done
clear
D)
lime
done
clear
View Answer play_arrow
question_answer 91) Formation of ammonia from \[{{\text{H}}_{\text{2}}}\]and \[{{\text{N}}_{2}}\]by Haber's process using Fe is an example of
A)
heterogeneous catalysis
done
clear
B)
homogeneous catalysis
done
clear
C)
enzyme catalysis
done
clear
D)
non-catalytic process
done
clear
View Answer play_arrow
question_answer 92) The reason for almost doubling the rate of reaction on increasing the temperature of the reaction system by \[10{{\,}^{o}}C\]is
A)
the value of threshold energy increases
done
clear
B)
collision frequency increases
done
clear
C)
the fraction of the molecule having energy equal to threshold energy increases
done
clear
D)
activation energy decreases
done
clear
View Answer play_arrow
question_answer 93) The pH of an aqueous solution having hydroxide ion concentration as \[1\times {{10}^{-5}}\] is
A)
5
done
clear
B)
9
done
clear
C)
4.5
done
clear
D)
11
done
clear
View Answer play_arrow
question_answer 94) Which of the following is not a Lewis acid?
A)
\[B{{F}_{3}}\]
done
clear
B)
\[AlC{{l}_{3}}\]
done
clear
C)
\[S{{O}_{2}}\]
done
clear
D)
\[{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 95) The precipitation takes place only when the product of concentrations of ions
A)
exceeds the solubility product
done
clear
B)
is less than the solubility product
done
clear
C)
is negligible
done
clear
D)
is equal to the solubility products
done
clear
View Answer play_arrow
question_answer 96) Which of the following has lowest electron affinity?
A)
\[Cl\]
done
clear
B)
\[I\]
done
clear
C)
\[F\]
done
clear
D)
\[Br\]
done
clear
View Answer play_arrow
question_answer 97) In the calcium fluoride structure the coordination number of the cation and anions are respectively
A)
6, 6
done
clear
B)
8, 4
done
clear
C)
4, 4
done
clear
D)
4, 8
done
clear
View Answer play_arrow
question_answer 98) The total number of orbitals possible for principal quantum number \[n\] is
A)
\[n\]
done
clear
B)
\[{{n}^{2}}\]
done
clear
C)
\[2n\]
done
clear
D)
\[2{{n}^{2}}\]
done
clear
View Answer play_arrow
question_answer 99) The pair having similar geometry is
A)
\[PC{{l}_{3}},N{{H}_{4}}\]
done
clear
B)
\[BeC{{l}_{2}},\,{{H}_{2}}O\]
done
clear
C)
\[C{{H}_{4}},CC{{l}_{4}}\]
done
clear
D)
\[I{{F}_{5}},P{{F}_{5}}\]
done
clear
View Answer play_arrow
question_answer 100) The \[d-\]orbital invovled in \[s{{p}^{3}}d-\]hybridisation is
A)
\[{{d}_{{{x}^{2}}-{{y}^{2}}}}\]
done
clear
B)
\[{{d}_{xy}}\]
done
clear
C)
\[{{d}_{{{z}^{2}}}}\]
done
clear
D)
\[{{d}_{zx}}\]
done
clear
View Answer play_arrow
question_answer 101) If 8.0 g of a radioactive substance has a half-life of 10 h, the half-life of 2.0 g of the same substance is
A)
2.6 h
done
clear
B)
5h
done
clear
C)
10 h
done
clear
D)
40 h
done
clear
View Answer play_arrow
question_answer 102) Loss of a beta paticle is equivalent to
A)
increase of one neutron only
done
clear
B)
decrease of one neutron only
done
clear
C)
both [a] and [b]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 103) Which of the following is incorrect?
A)
Relative lowering of vapour pressure is independent of the nature of the solute and the solvent
done
clear
B)
The ralative lowering of vapour pressure its a colligative property
done
clear
C)
Vapour pressure of a solution is lower than the vapour pressure of the solvent
done
clear
D)
The relative lowering of vapour pressure is directly proportional to the original pressure
done
clear
View Answer play_arrow
question_answer 104) The presence of the chlorine atom on benzene ring makes the second substituent enter at a position
A)
ortho
done
clear
B)
meta
done
clear
C)
para
done
clear
D)
ortho/para
done
clear
View Answer play_arrow
question_answer 105) Hydrogen is not obtained when zinc reacts with
A)
cold water
done
clear
B)
hot \[\text{NaOH}\]solution
done
clear
C)
dil \[{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\]
done
clear
D)
dil \[\text{HCl}\]
done
clear
View Answer play_arrow
question_answer 106) The oxidation number of xenon in \[\text{XeO}{{\text{F}}_{2}}\]is
A)
zero
done
clear
B)
2
done
clear
C)
4
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 107) Which of the following is most volatile?
A)
\[\text{HF}\]
done
clear
B)
\[\text{HCl}\]
done
clear
C)
\[\text{HBr}\]
done
clear
D)
\[\text{ }\!\!~\!\!\text{ HI}\]
done
clear
View Answer play_arrow
question_answer 108) The form of iron having the highest carbon content is
A)
cast iron
done
clear
B)
wrought ton
done
clear
C)
stainless steel
done
clear
D)
mild steel
done
clear
View Answer play_arrow
question_answer 109) Which belongs to the actinides series?
A)
\[Ce\]
done
clear
B)
\[~Cf\]
done
clear
C)
\[Ca~\]
done
clear
D)
\[~Cs\]
done
clear
View Answer play_arrow
question_answer 110) Which of the following is planar?
A)
\[Xe{{F}_{2}}\]
done
clear
B)
\[Xe{{O}_{3}}F\]
done
clear
C)
\[Xe{{O}_{2}}{{F}_{2}}\]
done
clear
D)
\[Xe{{F}_{4}}\]
done
clear
View Answer play_arrow
question_answer 111) \[\text{Cr}{{\text{O}}_{\text{3}}}\]dissovles in aqueous \[\text{NaOH}\]to give
A)
\[CrO_{4}^{2-}\]
done
clear
B)
\[Cr(OH)_{3}^{-}\]
done
clear
C)
\[C{{r}_{2}}O_{7}^{2-}\]
done
clear
D)
\[Cr{{(OH)}_{2}}\]
done
clear
View Answer play_arrow
question_answer 112) Which of the following is a tribasic acid?
A)
\[~{{H}_{3}}P{{O}_{4}}\]
done
clear
B)
\[~HP{{O}_{3}}\]
done
clear
C)
\[{{H}_{4}}{{P}_{2}}{{O}_{7}}\]
done
clear
D)
\[~{{H}_{4}}{{P}_{2}}{{O}_{6}}\]
done
clear
View Answer play_arrow
question_answer 113) Ethylene diamine is an example of
A)
monodentate ligand
done
clear
B)
bidentate ligand
done
clear
C)
tridentate ligand
done
clear
D)
polydentate ligand
done
clear
View Answer play_arrow
question_answer 114) The molecule having a pyramidal shape out of the following is
A)
\[C{{O}_{2}}\]
done
clear
B)
\[~B{{F}_{3}}\]
done
clear
C)
\[S{{F}_{4}}\]
done
clear
D)
\[~N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 115) Which of the following doesn't give a ppt. with silver nitrate solution?
A)
Ethyl bromide
done
clear
B)
Sodium bromide
done
clear
C)
Calcium chloride
done
clear
D)
Sodium chloride
done
clear
View Answer play_arrow
question_answer 116) Which is the most stable carbocation?
A)
\[iso-\]propyl cation
done
clear
B)
Triphenylmethyl cation
done
clear
C)
Ethyl cation
done
clear
D)
\[n-\]propyl cation
done
clear
View Answer play_arrow
question_answer 117) Which is most acidic of the following?
A)
Methane
done
clear
B)
Acetylene
done
clear
C)
1-butene
done
clear
D)
Neo-pentane
done
clear
View Answer play_arrow
question_answer 118) Which is the most reactive of the following?
A)
Ethyl acetate
done
clear
B)
Acetic anhydride
done
clear
C)
Acetamide
done
clear
D)
Acetyl chloride
done
clear
View Answer play_arrow
question_answer 119) Which of the following will be chiral?
A)
\[C{{H}_{3}}CHC{{l}_{2}}\]
done
clear
B)
\[C{{H}_{3}}CHBrCl\]
done
clear
C)
\[C{{D}_{2}}C{{l}_{2}}\]
done
clear
D)
\[C{{H}_{2}}ClBr\]
done
clear
View Answer play_arrow
question_answer 120) Electronic configuration of deuterium atom is
A)
\[1{{s}^{1}}\]
done
clear
B)
\[2{{s}^{2}}\]
done
clear
C)
\[2{{s}^{1}}\]
done
clear
D)
\[1{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 121) Which of the following is a phenol?
A)
Pentanoic acid
done
clear
B)
Phthalic acid
done
clear
C)
Picric acid
done
clear
D)
Phosphoric acid
done
clear
View Answer play_arrow
question_answer 122) Which of the following is not an organometallic compound?
A)
\[{{C}_{2}}{{H}_{5}}ONa\]
done
clear
B)
\[C{{H}_{3}}MgI\]
done
clear
C)
Tetraethyl
done
clear
D)
\[K{{C}_{4}}{{H}_{9}}\]
done
clear
View Answer play_arrow
question_answer 123) The correct order of electron affinity is
A)
\[B<C<O>N\]
done
clear
B)
\[B>C>N>O\]
done
clear
C)
\[\text{O}>C>B>N\]
done
clear
D)
\[\text{O}<C<B<N\]
done
clear
View Answer play_arrow
question_answer 124) Ziegler Natta catalyst is an organometallic compound containing
A)
iron
done
clear
B)
titanium
done
clear
C)
rhodium
done
clear
D)
zirconium
done
clear
View Answer play_arrow
question_answer 125) Which of the following cannot undergo nucleophilic substitution under ordinary conditions?
A)
Chlorobenzene
done
clear
B)
Tert-butylchloride
done
clear
C)
Isopropyl chloride
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 126) The compound which contains all the four\[{{1}^{o}},{{2}^{o}},{{3}^{o}}\]and \[{{4}^{o}}\] carbon atoms is
A)
\[2,3-\]dimethyl pentane
done
clear
B)
\[3-\]chloro\[-2,3-\]dimethylpentane
done
clear
C)
\[2,3,4-\]trimethylpentane
done
clear
D)
\[3,3-\]dimethylpentane
done
clear
View Answer play_arrow
question_answer 127) Brass, bronze and german silver have one common metal. This is
A)
Zn
done
clear
B)
Fe
done
clear
C)
Al
done
clear
D)
Cu
done
clear
View Answer play_arrow
question_answer 128) Which of the following is the green coloured powder produced when ammoniunium dichromate is used in fire works?
A)
\[Zn\]
done
clear
B)
\[Fe\]
done
clear
C)
\[Al\]
done
clear
D)
\[Cu\]
done
clear
View Answer play_arrow
question_answer 129) The \[\pi -\]bonded organometallic compound which has ethene as one of its component is
A)
Zeise's salt
done
clear
B)
ferrocene
done
clear
C)
dibenzene chromium
done
clear
D)
tetraethyl tin
done
clear
View Answer play_arrow
question_answer 130) Malachite is an ore of
A)
\[Fe\]
done
clear
B)
\[Ag\]
done
clear
C)
\[Cr\]
done
clear
D)
\[Cu\]
done
clear
View Answer play_arrow
question_answer 131) The most acidic of the following is
A)
\[ClC{{H}_{2}}COOH\]
done
clear
B)
\[{{C}_{6}}{{H}_{5}}COOH\]
done
clear
C)
\[C{{D}_{3}}COOH\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}COOH\]
done
clear
View Answer play_arrow
question_answer 132) Which of the following is an electrophile?
A)
\[{{H}_{2}}O\]
done
clear
B)
\[S{{O}_{3}}\]
done
clear
C)
\[~N{{H}_{3}}\]
done
clear
D)
\[~ROR\]
done
clear
View Answer play_arrow
question_answer 133) An aromatic compound among other things should have a\[\pi -\]electron cloud containing \[(4n+2)\,\pi \]electrons where \[n\]can't be
A)
1/2
done
clear
B)
3
done
clear
C)
2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 134) Glycerol is an alcohol which can be classified as
A)
trihydric
done
clear
B)
monohydric
done
clear
C)
dihydric
done
clear
D)
hexahydric
done
clear
View Answer play_arrow
question_answer 135) The oxidation number of cobalt in \[K[Co{{(CO)}_{4}}]\]is
A)
\[+\,1\]
done
clear
B)
\[+\,3\]
done
clear
C)
\[~-1\]
done
clear
D)
\[-3\]
done
clear
View Answer play_arrow
question_answer 136) Bromination of alkanes involves
A)
carbanions
done
clear
B)
carbocations
done
clear
C)
carbenes
done
clear
D)
free radicals
done
clear
View Answer play_arrow
question_answer 137) Methylphenyl ether can be obtained by reacting
A)
phenolate ions and methyl iodide
done
clear
B)
methoxide ipns and bromobenzene
done
clear
C)
methanol and phenol
done
clear
D)
bromo benzene and methyl bromide
done
clear
View Answer play_arrow
question_answer 138) Which is not correct?
A)
Phenol is more acidic than acetic acid
done
clear
B)
Ethanol is less acidic than phenol
done
clear
C)
Ethanol has higher boiling point than ethane
done
clear
D)
Ethane is a non-linear molecule
done
clear
View Answer play_arrow
question_answer 139) Ascorbic acid is also known as
A)
vitamin A
done
clear
B)
vitamin B
done
clear
C)
vitamin C
done
clear
D)
vitamin D
done
clear
View Answer play_arrow
question_answer 140) Reaction of phenol with chloroform/sodium hydroxide to give \[o-\]hydroxy benzaldehyde involves the formation of
A)
dichloro carbine
done
clear
B)
trichloro carbene
done
clear
C)
chlorine atoms
done
clear
D)
chlorine molecules
done
clear
View Answer play_arrow
question_answer 141) One of the following that cannot undergo dehydrohalogenation is
A)
\[iso-\]propyl bromide
done
clear
B)
ethariol
done
clear
C)
ethyl bromide
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 142) Which requires catalyst?
A)
\[S+{{O}_{2}}\to S{{O}_{2}}\]
done
clear
B)
\[2S{{O}_{2}}+\,{{O}_{2}}\to 2S{{O}_{3}}\]
done
clear
C)
\[C+{{O}_{2}}\to C{{O}_{2}}\]
done
clear
D)
All of these
done
clear
View Answer play_arrow
question_answer 143) Acetic acid will be obtained on oxidation of
A)
ethanol
done
clear
B)
propanal
done
clear
C)
methanal
done
clear
D)
glyoxal
done
clear
View Answer play_arrow
question_answer 144) A carboxylic acid is converted into its anhydride using
A)
thionyl chloride
done
clear
B)
sulphur chloride
done
clear
C)
sulphuric acid
done
clear
D)
phosphorus pentoxide
done
clear
View Answer play_arrow
question_answer 145) Which is false?
A)
Glucose is a disaccharide
done
clear
B)
Starch is a polysaccharide
done
clear
C)
Glucose and fructose are not anomers
done
clear
D)
Invert sugar consists of glucose and fructose
done
clear
View Answer play_arrow
question_answer 146) What kind of isomerism is possible for 1-chloro-2-nitroethene?
A)
Functional group isomerism
done
clear
B)
Position isomerism
done
clear
C)
E/Z isomerism
done
clear
D)
Optical isomerism
done
clear
View Answer play_arrow
question_answer 147) KCN reacts readily to give a cyanide with
A)
ethyl alcohol
done
clear
B)
ethyl bromide
done
clear
C)
bromobenzene
done
clear
D)
chlorobenzene
done
clear
View Answer play_arrow
question_answer 148) Peptides are formed from
A)
aliphatic amines
done
clear
B)
carbohydrates
done
clear
C)
a-amino acids
done
clear
D)
aromatic amines
done
clear
View Answer play_arrow
question_answer 149) Calcium carbide on reaction with water yields
A)
methane
done
clear
B)
ethane
done
clear
C)
ethene
done
clear
D)
ethyne
done
clear
View Answer play_arrow
question_answer 150) The correct set of the four quantum numbers of a \[4d\] electron is
A)
\[4,2,1-\frac{1}{2}\]
done
clear
B)
\[4,2,1,0\]
done
clear
C)
\[4,3,2,+\frac{1}{2}\]
done
clear
D)
\[4,3,-2,+\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 151) In a class of 30 pupils. 12 take needls work, 16 take physics and 18 take history. If all the 30 students take at least one subject and no one takes all three, then the number of pupils taking 2 subjects is
A)
\[16\]
done
clear
B)
\[6\]
done
clear
C)
\[8\]
done
clear
D)
\[20\]
done
clear
View Answer play_arrow
question_answer 152) If \[f(2x+3)=\sin x+{{2}^{x}},\] then \[f(4m-2n+3)\] is equal to
A)
\[\sin \,(m-2n)+{{2}^{2m-n}}\]
done
clear
B)
\[\sin \,(2m-n)+{{2}^{(m-n)2}}\]
done
clear
C)
\[\sin \,(m-2n)+{{2}^{(m+n)2}}\]
done
clear
D)
\[\sin (2m-n)+{{2}^{2m-n}}\]
done
clear
View Answer play_arrow
question_answer 153) If \[{{z}_{1}}=1+2i\] and \[{{z}_{2}}=3+5i,\] then \[\operatorname{Re}[{{\bar{z}}_{2}}{{z}_{1}}/{{z}_{2}}]\]is equal to
A)
\[-31/17\]
done
clear
B)
\[17/22\]
done
clear
C)
\[-17/31\]
done
clear
D)
\[22/17\]
done
clear
View Answer play_arrow
question_answer 154) If \[|z+8|+|z-8|=16,\] where z is a complex number, then the point z will lie on
A)
circle
done
clear
B)
an ellipse
done
clear
C)
a straight line
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 155) If twice the 11 th term of an AP is equal to 7times its 21st term, then its 25th term is equal to
A)
\[24\]
done
clear
B)
\[120\]
done
clear
C)
\[0\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 156) If one of the roots of equation \[{{x}^{2}}+ax+3=0\] is 3 and one of the roots of the equation \[{{x}^{2}}+ax+b=0\]is three times the other root, then the value of b is equal to
A)
\[3\]
done
clear
B)
\[4\]
done
clear
C)
\[2\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 157) If S is the sum of an infinite GP, the first term a, then the common ratio r is given by
A)
\[\frac{a-S}{S}\]
done
clear
B)
\[\frac{S-a}{S}\]
done
clear
C)
\[\frac{a}{1-S}\]
done
clear
D)
\[\frac{S-a}{a}\]
done
clear
View Answer play_arrow
question_answer 158) The coefficient of \[{{x}^{4}}\]in the expansion of \[{{\left( \frac{x}{2}-\frac{3}{{{x}^{2}}} \right)}^{10}}\]is.
A)
\[405/226\]
done
clear
B)
\[504/289\]
done
clear
C)
\[450/263\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 159) The figure formed by joining the points \[(4,0)\] s\[(3,5)\]and \[(-1,-1)\] in pairs is
A)
a right angled triangle
done
clear
B)
an acute angled triangle
done
clear
C)
an obtuse angled triangle
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 160) The ortho centre of the triangle with vertices \[(-2,-6),\,\,\,(-2,4)\] and \[(1,3)\] is
A)
\[(3,\,1)\]
done
clear
B)
\[(1,\,1/3)\]
done
clear
C)
\[(1,3)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 161) The in centre of a triangle with vertices \[(7,1),\] \[(-1,5)\] and \[(3+2\sqrt{3},3+4\sqrt{3})\]is
A)
\[\left( 3+\frac{2}{\sqrt{3}},\,3+\frac{4}{\sqrt{3}} \right)\]
done
clear
B)
\[\left( 1+\frac{2}{3\sqrt{3}},1+\frac{4}{3\sqrt{3}} \right)\]
done
clear
C)
\[(7,1)\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 162) Let a be the distance between line \[-x+y=2\] and \[x-y=2\]and \[\beta \] be the distance between the lines \[4x-3y=5\] and \[6y-8x=1,\] then
A)
\[20\sqrt{2}\beta =11\alpha \]
done
clear
B)
\[20\sqrt{2}\alpha =11\beta \]
done
clear
C)
\[11\sqrt{2}\beta =20\alpha \]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 163) The equations of the tangents to circle \[5{{x}^{2}}+5{{y}^{2}}=1,\] parallel to line \[3x+4y=1\] are
A)
\[3x+4y=\pm 2\sqrt{5}\]
done
clear
B)
\[6x+8y=\pm \sqrt{5}\]
done
clear
C)
\[3x+4y=\pm \sqrt{5}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 164) From the point \[(-1,-6)\] two tangents are drawn to the parabola\[{{y}^{2}}=4x\]. Then, the angle between the two tangents is
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{45}^{o}}\]
done
clear
C)
\[{{60}^{o}}\]
done
clear
D)
\[{{90}^{o}}\]
done
clear
View Answer play_arrow
question_answer 165) If the foci of an ellipse are \[(\pm \sqrt{5},0)\] and its eccentricity is \[\sqrt{5}/3,\] then the equation of the ellipse is
A)
\[9{{x}^{2}}+4{{y}^{2}}=36\]
done
clear
B)
\[4{{x}^{2}}+9{{y}^{2}}=36\]
done
clear
C)
\[36{{x}^{2}}+9{{y}^{2}}=4\]
done
clear
D)
\[9{{x}^{2}}+36{{y}^{2}}=4\]
done
clear
View Answer play_arrow
question_answer 166) If \[y=(1+\tan \,A)\,(1-\tan B),\]where \[A-B=\frac{\pi }{4},\]then \[{{(y+1)}^{y+1}}\] is equal to
A)
\[9\]
done
clear
B)
\[4\]
done
clear
C)
\[27\]
done
clear
D)
\[81\]
done
clear
View Answer play_arrow
question_answer 167) If \[x\,\,\sin \theta -y\,\cos \,\theta =0\]and \[x\,{{\sin }^{3}}\theta +y\,{{\cos }^{3}}\theta =\sin \theta \,\,\cos \theta ,\] then \[{{x}^{2}}+{{y}^{2}}\] is equal to
A)
\[0\]
done
clear
B)
\[2\]
done
clear
C)
\[4\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 168) If \[\tan x=\frac{b}{a},\] then the value of \[a\,\cos \,2x+b\,\sin \,2x\]is
A)
\[a\]
done
clear
B)
\[b\]
done
clear
C)
\[a+b\]
done
clear
D)
\[{{a}^{2}}+{{b}^{2}}\]
done
clear
View Answer play_arrow
question_answer 169) If the expansion in powers of x of the function \[\frac{1}{(1-ax)\,(1-bx)}\]is \[{{a}_{0}}-{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+{{a}_{3}}{{x}^{3}}+.....,\] then \[{{a}_{n}}\] is
A)
\[\frac{{{b}^{n+1}}-{{a}^{n+1}}}{b-a}\]
done
clear
B)
\[\frac{{{a}^{n}}-{{b}^{n}}}{b-a}\]
done
clear
C)
\[\frac{{{a}^{n+1}}-{{b}^{n+1}}}{b-a}\]
done
clear
D)
\[\frac{{{b}^{n}}-{{a}^{n}}}{b-a}\]
done
clear
View Answer play_arrow
question_answer 170) If n is any integer, then the general solution of the equation \[\cos \theta -\sin \theta =\frac{1}{\sqrt{2}}\] is
A)
\[\theta =2n\pi -\frac{\pi }{12}\] or\[\theta =2n\pi +\frac{7\pi }{12}\]
done
clear
B)
\[\theta =n\pi +\frac{\pi }{12}\]
done
clear
C)
\[\theta =2n\pi +\frac{\pi }{12}\] or \[\theta =2n\pi -\frac{7\pi }{12}\]
done
clear
D)
\[\theta =2n\pi +\frac{\pi }{12}\] or \[\theta =2n\pi -\frac{7\pi }{12}\]
done
clear
View Answer play_arrow
question_answer 171) . The value of \[{{\cos }^{-1}}\,(\cos \,12)-{{\sin }^{-1}}\,(\sin 14)\] is
A)
\[-2\]
done
clear
B)
\[8\pi -26\]
done
clear
C)
\[4\pi +2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 172) If a, b and c are the sides of a triangle such that \[{{a}^{4}}+{{b}^{4}}+{{c}^{4}}=2{{c}^{2}}({{a}^{2}}+{{b}^{2}}),\] then the angles opposite to the side C is
A)
\[{{45}^{o}}\] or \[{{90}^{o}}\]
done
clear
B)
\[{{30}^{o}}\] or \[{{135}^{o}}\]
done
clear
C)
\[{{45}^{o}}\] or \[{{135}^{o}}\]
done
clear
D)
\[{{60}^{o}}\] or \[{{120}^{o}}\]
done
clear
View Answer play_arrow
question_answer 173) The value of the determinant \[\left| \begin{matrix} 0 & {{b}^{3}}-{{a}^{3}} & {{c}^{3}}-{{a}^{3}} \\ {{a}^{3}}-{{b}^{3}} & 0 & {{c}^{3}}-{{b}^{3}} \\ {{a}^{3}}-{{c}^{3}} & {{b}^{3}}-{{c}^{3}} & 0 \\ \end{matrix} \right|\]is equal to
A)
\[{{a}^{3}}-{{b}^{3}}-{{c}^{3}}\]
done
clear
B)
\[{{a}^{3}}-{{b}^{3}}-{{c}^{3}}\]
done
clear
C)
\[0\]
done
clear
D)
\[-{{a}^{3}}+{{b}^{3}}+{{c}^{3}}\]
done
clear
View Answer play_arrow
question_answer 174) The integer represented by the determinant \[\left| \begin{matrix} 215 & 342 & 511 \\ 6 & 7 & 8 \\ 36 & 49 & 54 \\ \end{matrix} \right|\] is exactly divisible by
A)
\[146\]
done
clear
B)
\[21\]
done
clear
C)
\[20\]
done
clear
D)
\[335\]
done
clear
View Answer play_arrow
question_answer 175) A root of the equation \[\left| \begin{matrix} 3-x & -6 & 3 \\ -6 & 3-x & 3 \\ 3 & 3 & -6-x \\ \end{matrix} \right|=0\] is given by
A)
\[x=0\]
done
clear
B)
\[x=6\]
done
clear
C)
\[x=3\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 176) The determinant \[\left| \begin{matrix} 4+{{x}^{2}} & -6 & -2 \\ -6 & 9+{{x}^{2}} & 3 \\ -2 & 3 & 1+{{x}^{2}} \\ \end{matrix} \right|\] is not divisible by
A)
\[x\]
done
clear
B)
\[{{x}^{3}}\]
done
clear
C)
\[14+{{x}^{2}}\]
done
clear
D)
\[{{x}^{5}}\]
done
clear
View Answer play_arrow
question_answer 177) If X is a square matrix of order \[3\times 3,\lambda \] is a scalar, then adj \[(\lambda x)\]is equal to
A)
\[\lambda \,\,adj\,\,(X)\]
done
clear
B)
\[{{\lambda }^{3}}\,\,adj\,\,(X)\]
done
clear
C)
\[{{\lambda }^{2}}\,\,adj\,\,(X)\]
done
clear
D)
\[{{\lambda }^{4}}\,\,adj\,\,(X)\]
done
clear
View Answer play_arrow
question_answer 178) If \[f(\theta )=\left[ \begin{matrix} \cos \,\theta & -\sin \theta & 0 \\ \sin \,\theta & \cos \,\theta & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right],\]then \[{{\{f(\theta )\}}^{-1}}\]is equal to
A)
\[f(-\theta )\]
done
clear
B)
\[f(-\theta )\]
done
clear
C)
\[f(2\theta )\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 179) The minors of \[-4\] and \[9\] and the cofactors of \[-4\]and 9 in matrix \[\left[ \begin{matrix} -1 & -2 & 3 \\ -4 & -5 & -6 \\ -7 & 8 & 9 \\ \end{matrix} \right]\] are respectively
A)
\[42,3,-42,3\]
done
clear
B)
\[-42,-3,42\]
done
clear
C)
\[42,3,42,3,-3\]
done
clear
D)
\[42,3,-42,3\]
done
clear
View Answer play_arrow
question_answer 180) If \[X=\left[ \begin{matrix} -x & -y \\ z & t \\ \end{matrix} \right],\] then transpose of adj (X) is
A)
\[\left[ \begin{matrix} t & z \\ -y & -x \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} t & y \\ -z & -x \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} t & -z \\ y & -x \\ \end{matrix} \right]\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 181) Let PQRS be a parallelogram whose diagonals PR and QS intersect at O?. If O is origin, then \[\overrightarrow{OP}+\overrightarrow{OQ}+\overrightarrow{OR}+\overrightarrow{OS}\]is equal to
A)
\[\overrightarrow{OO'}\]
done
clear
B)
\[2\overrightarrow{O}O'\]
done
clear
C)
\[3\overrightarrow{O}Q'\]
done
clear
D)
\[4\overrightarrow{O}O'\]
done
clear
View Answer play_arrow
question_answer 182) If the vectors \[2\hat{i}+\hat{j}-\hat{k},-\hat{i}+2\hat{j}+\lambda \hat{k}\] and \[-5\,\hat{i}+2\hat{j}-\hat{k}\]are coplanar, then the value of \[\lambda \] is equal to
A)
\[-13\]
done
clear
B)
\[13/9\]
done
clear
C)
\[-13/9\]
done
clear
D)
\[-9/13\]
done
clear
View Answer play_arrow
question_answer 183) If the scalar projection of the vectors \[x\,\hat{i}+\hat{j}+\hat{k}\] on the vector \[2\hat{i}-\hat{j}+5\hat{k}\] is \[\frac{1}{\sqrt{30}},\] then the value of x is
A)
\[-3/2\]
done
clear
B)
\[6\]
done
clear
C)
\[-6\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 184) If \[\vec{x}+\vec{y}+\vec{z}=\vec{0},\,|\vec{x}|=|\vec{y}|=|\vec{z}|=2\] and \[\theta \] is angle between \[\vec{y}\] and \[\vec{z},\] then the value of \[\text{cose}{{\text{c}}^{2}}\theta +{{\cot }^{2}}\theta \] is equal to
A)
\[4/3\]
done
clear
B)
\[5/3\]
done
clear
C)
\[1/3\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 185) If the position vectors of two points P and Q are respectively \[9\,\hat{i}-\hat{j}+5\hat{k}\]and \[\hat{i}+3\hat{j}+5\hat{k}\] and the line segment PQ intersects the YOZ plane at a point R, then \[PR:RQ\]is equal to
A)
\[9:1\]
done
clear
B)
\[1:9\]
done
clear
C)
\[-1:9\]
done
clear
D)
\[-9:1\]
done
clear
View Answer play_arrow
question_answer 186) If \[\vec{u},\vec{v}\] and \[\vec{w}\] are three mutually perpendicular unit vectors, then \[|\vec{u}+\vec{v}+\vec{w}|\]is equal to
A)
\[\sqrt{3}\]
done
clear
B)
\[1\]
done
clear
C)
\[3\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 187) The angle between the vectors \[\vec{a}+\vec{b}\] and \[\vec{a}-\vec{b}\]when \[\vec{a}=(1,1,4)\] and \[\vec{b}=(1,-1,4)\] is
A)
\[{{90}^{o}}\]
done
clear
B)
\[{{45}^{o}}\]
done
clear
C)
\[{{30}^{o}}\]
done
clear
D)
\[{{15}^{o}}\]
done
clear
View Answer play_arrow
question_answer 188) The line of intersection of the planes \[\vec{r}.(\hat{i}-3\hat{j}+\hat{k})=1\] and \[\vec{r}.(2\hat{i}+5\hat{j}-3\hat{k})=2\] is parallel to the vector
A)
\[-4\hat{i}+5\hat{j}+11\hat{k}\]
done
clear
B)
\[4\hat{i}+5\hat{j}+11\hat{k}\]
done
clear
C)
\[-4\hat{i}-5\hat{j}+11\hat{k}\]
done
clear
D)
\[-4\hat{i}+5\hat{j}-11\hat{k}\]
done
clear
View Answer play_arrow
question_answer 189) A plane meet the coordinate axes at P, Q and R such that the position vector of the centroid of \[\Delta PQR\] is \[2\hat{i}-5\hat{j}+8\hat{k}\]. Then, the equation of the plane is
A)
\[\vec{r}.(20\,\hat{i}-8\hat{j}+5\hat{k})=120\]
done
clear
B)
\[\vec{r}.(20\,\hat{i}-8\hat{j}+5\hat{k})=1\]
done
clear
C)
\[\vec{r}.(20\,\hat{i}-8\hat{j}+5\hat{k})=2\]
done
clear
D)
\[\vec{r}.(20\,\hat{i}-8\hat{j}+5\hat{k})=20\]
done
clear
View Answer play_arrow
question_answer 190) The distance of the point \[(2,3,4)\] from the line \[1-x=\frac{y}{2}=\frac{1}{3}(1+z)\] is
A)
\[\frac{1}{7}\sqrt{35}\]
done
clear
B)
\[\frac{4}{7}\sqrt{35}\]
done
clear
C)
\[\frac{2}{7}\sqrt{35}\]
done
clear
D)
\[\frac{3}{7}\sqrt{35}\]
done
clear
View Answer play_arrow
question_answer 191) The equation of the plane passing through the points \[(0,1,2)\] and \[(-1,\,0,3)\] and perpendicular to the plane \[2x+3y+z=5\] is
A)
\[3x-4y+18z+32=0\]
done
clear
B)
\[3x+4y-18x+32=0\]
done
clear
C)
\[4x+3y-17z+31=0\]
done
clear
D)
\[4x-3y+z+1=0\]
done
clear
View Answer play_arrow
question_answer 192) A line joining the points \[(1,2,0)\] and \[(4,13,5)\] is perpendicular to a plane. Then, the coefficients of x, y and z in the equation of the plane are; respectively
A)
\[5,15,5\]
done
clear
B)
\[3,11,5\]
done
clear
C)
\[3,-11,5\]
done
clear
D)
\[-5,-15,5\]
done
clear
View Answer play_arrow
question_answer 193) The image of the point \[P(1,3,4)\] in the plane \[2x-y+z+3=0\] is
A)
\[(3,\,5,-2)\]
done
clear
B)
\[(-3,\,5,2)\]
done
clear
C)
\[(3,-5,2)\]
done
clear
D)
\[(-1,\,4,2)\]
done
clear
View Answer play_arrow
question_answer 194) The distance between the line \[\vec{r}=2\hat{i}-2\hat{j}+3\hat{k}+\lambda (\hat{i}-\hat{j}+4\hat{k})\] and the plane \[\vec{r}.(\hat{i}+5\hat{j}+\hat{k})=5\] is
A)
\[\frac{10}{3}\]
done
clear
B)
\[\frac{3}{10}\]
done
clear
C)
\[\frac{10}{3\sqrt{3}}\]
done
clear
D)
\[\frac{10}{9}\]
done
clear
View Answer play_arrow
question_answer 195) The distance between the planes \[2x+y+2z=8\]and \[4x+2y+4z+5=0\]
A)
\[3/2\]
done
clear
B)
\[7/2\]
done
clear
C)
\[2/5\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 196) If \[\alpha ,\beta \] and \[\gamma \] are the roots of equation \[{{x}^{3}}-3{{x}^{2}}+x+5=0,\] then \[y=\Sigma {{\alpha }^{2}}+\alpha \beta \gamma \]satisfies the equation.
A)
\[{{y}^{3}}+y+2=0\]
done
clear
B)
\[{{y}^{3}}-{{y}^{2}}-y-2=0\]
done
clear
C)
\[{{y}^{3}}+3{{y}^{2}}-y-3=0\]
done
clear
D)
\[{{y}^{2}}+4{{y}^{2}}+5y+20=0\]
done
clear
View Answer play_arrow
question_answer 197) If l(x) is the least integer not less than x and g(,x) is the greatest integer not greater than x, then \[\underset{x\to e+\pi }{\mathop{\lim }}\,\{l(x)+g(x)\}\] is equal to
A)
\[9\]
done
clear
B)
\[13\]
done
clear
C)
\[1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 198) The value of \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{27}^{x}}-{{9}^{x}}-{{3}^{x}}+1}{\sqrt{5}-\sqrt{4}+\cos x}\] is
A)
\[\sqrt{5}\,{{(\log 3)}^{2}}\]
done
clear
B)
\[8\sqrt{5}\,{{(\log 3)}^{2}}\]
done
clear
C)
\[16\sqrt{5}\,(\log 3)\]
done
clear
D)
\[10\sqrt{5}\,{{(\log 3)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 199) The value of \[\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{x}^{n}}}{{{x}^{n}}+1},\]where \[x<-1\] is
A)
\[1/2\]
done
clear
B)
\[-1/2\]
done
clear
C)
\[1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 200) The value of \[\underset{x\to \pi /2}{\mathop{\lim }}\,\,\frac{{{2}^{\cot \,x}}-{{2}^{\cos \,x}}}{\cot \,x-\,\cos \,x}\]is
A)
\[\log \,2\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 201) The point of discontinuity of tan x is
A)
\[x=n\pi \]
done
clear
B)
\[x=n\pi /6\]
done
clear
C)
\[x=(2n+1)\pi /2\]
done
clear
D)
\[x=n\pi /3\]
done
clear
View Answer play_arrow
question_answer 202) Let \[f(x)=\left\{ \begin{matrix} (1/2)\,\{g(x)+(x)\}\,\,sin\,(x),\,x\ge 1 \\ \sin \,x/x,\,x<1 \\ \end{matrix} \right.\] where \[g(x)=\left\{ \begin{matrix} 1, & if & x>0 \\ -1, & if & x<0 \\ 0, & if & x=0 \\ \end{matrix} \right.\] Then, \[\underset{x\to 1}{\mathop{\lim }}\,\,\,f(x)\] is equal to
A)
\[0\]
done
clear
B)
\[2\]
done
clear
C)
\[sin\text{ }1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 203) The function \[f(x)=\frac{2{{x}^{2}}+7}{{{x}^{3}}+3{{x}^{2}}-x-3}\]is discontinuous for
A)
\[x=1\]only
done
clear
B)
\[x=1\] and \[x=-1\]only
done
clear
C)
\[x=1,\,x=-1,\,x=-3\]only
done
clear
D)
\[x=1,\,x=-1,\,x=-3\] and other values of x
done
clear
View Answer play_arrow
question_answer 204) If \[f(x)=\left\{ \begin{matrix} x, & for & <x<1 \\ 2-x, & for & 1\le x<2 \\ x-(1/2){{x}^{2}}, & for & x=2 \\ \end{matrix} \right.\] Then, \[f'(1)\]is equal to
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
\[0\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 205) If \[y={{\cos }^{-1}}\cos (|x|-f(x)),\] where \[f(x)=\left\{ \begin{matrix} 1, & if & x>0 \\ -1, & if & x<0 \\ 0, & if & x=0 \\ \end{matrix} \right.\] Then, \[{{(dy/dx)}_{x=\frac{5\pi }{4}}}\]is equal to
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
\[0\]
done
clear
D)
can't be determined
done
clear
View Answer play_arrow
question_answer 206) If \[{{x}^{m}}{{y}^{n}}={{(x+y)}^{m+n}},\] then \[{{(dy/dx)}_{x=1,\,y=2}}\] is equal to
A)
\[1/2\]
done
clear
B)
\[2\]
done
clear
C)
\[2m/n\]
done
clear
D)
\[~m/2n\]
done
clear
View Answer play_arrow
question_answer 207) The function \[f(x)=2{{x}^{3}}-3{{x}^{2}}+90x+174\] is increasing in the interval
A)
\[1/2<x<1\]
done
clear
B)
\[1/2<x<2\]
done
clear
C)
\[3<x<59/4\]
done
clear
D)
\[-\infty <x<\infty \]
done
clear
View Answer play_arrow
question_answer 208) The equation of the tangent to the curve \[x=2\,{{\cos }^{3}}\theta \] and \[y=3\,{{\sin }^{3}}\theta \] at the point \[\theta =\pi /4\] is
A)
\[2x+3y=3\sqrt{2}\]
done
clear
B)
\[2x-3y=3\sqrt{2}\]
done
clear
C)
\[3x+2y=3\sqrt{2}\]
done
clear
D)
\[3x-2y=3\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 209) The minimum value of \[4{{e}^{2x}}+9{{e}^{-2x}}\] is
A)
\[11\]
done
clear
B)
\[12\]
done
clear
C)
\[10\]
done
clear
D)
\[14\]
done
clear
View Answer play_arrow
question_answer 210) The point of parabola \[2y={{x}^{2}},\] which is nearest to the point \[(0,\,\,3)\] is
A)
\[(\pm 4,\,8)\]
done
clear
B)
\[(\pm 1,1/2)\]
done
clear
C)
\[(\pm 2,2)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 211) In the mean value theorem \[f(b)-f(a)=(b-a)\,f'(c),\] if \[a=4,\text{ }b=9\]and \[f(x)=\sqrt{x},\] then the value of c is
A)
\[8.00\]
done
clear
B)
\[5.25\]
done
clear
C)
\[4.00\]
done
clear
D)
\[6.25\]
done
clear
View Answer play_arrow
question_answer 212) If x is any arbitrary constant, then \[\int{{{2}^{{{2}^{{{2}^{x}}}}}}}.\,{{2}^{{{2}^{x}}}}.\,{{2}^{x}}\,\,dx\]is equal to
A)
\[\frac{\int{{{2}^{{{2}^{x}}}}}\,dx}{{{(In\,\,2)}^{3}}}+c\]
done
clear
B)
\[\frac{\int{{{2}^{{{2}^{{{2}^{x}}}}}}}\,dx}{{{(In\,\,2)}^{3}}}+c\]
done
clear
C)
\[\int{{{2}^{{{2}^{{{2}^{x}}}}}}}\,\,{{(In\,\,2)}^{3}}+c\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 213) The derivative of function \[f(x)\] is \[{{\tan }^{4}}x\]. If \[f(x)=0,\] then \[\underset{x\to 0}{\mathop{\lim }}\,\frac{f(x)}{x}\]is equal to
A)
\[1\]
done
clear
B)
\[0\]
done
clear
C)
\[-1\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 214) The value of \[\int_{1}^{{{e}^{2}}}{\frac{dx}{x{{(1+\log \,x)}^{2}}}}\] is
A)
\[2/3\]
done
clear
B)
\[1/3\]
done
clear
C)
\[3/2\]
done
clear
D)
In 2
done
clear
View Answer play_arrow
question_answer 215) If \[2f(x)-3f(1/x)=x,\] then \[\int_{1}^{2}{f(x)\,\,dx}\] is equal to
A)
\[(3/5)\] In 2
done
clear
B)
\[(-3/5)\] (\[1+\]In 2)
done
clear
C)
\[(-3/5)\] In 2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 216) If A is the area of the region bounded by the curve \[y=\sqrt{3x+4},\] x-axis and the lines \[x=-1\]and \[x=4\]and B is that area bounded by curve \[{{y}^{2}}=3x+4,\]x axis and the lines \[x=-1\]and \[x=4,\] then \[A:B\]is equal to
A)
\[1:1\]
done
clear
B)
\[2:1\]
done
clear
C)
\[1:2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 217) If c is an arbitrary constant, then the general solution of the differential equation \[ydx-xdy=xy\,\,dx\]is given by
A)
\[y=cx{{e}^{-x}}\]
done
clear
B)
\[y=cy{{e}^{-x}}\]
done
clear
C)
\[y+{{e}^{-x}}=cx\]
done
clear
D)
\[y{{e}^{x}}=cx\]
done
clear
View Answer play_arrow
question_answer 218) The solution of \[dy=\cos \,x(2-y\,\text{cosec x)}\,\text{dx}\]where \[y=\sqrt{2},\] when \[x=\pi /4\] is
A)
\[y\sin \,x+\frac{1}{2}\,\text{cosec x}\]
done
clear
B)
\[y=\tan \,(x/2)+\cot (x/2)\]
done
clear
C)
\[y=(1/\sqrt{2})\,\sec \,(x/2)+\sqrt{2}\,\cos \,\,(x/2)\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 219) The probability that at least one of the event A and B occurs is \[0.6\]. If A and B occur simultaneously with probability \[0.2,\] then \[P(\bar{A})+P(\bar{B})\]is equal to
A)
\[0.4\]
done
clear
B)
\[0.8\]
done
clear
C)
\[1.2\]
done
clear
D)
\[1.4\]
done
clear
View Answer play_arrow
question_answer 220) A die is thrown. If it shows a six, we draw a ball from a bag consisting, if 2 black balls and 6 white balls. If it does not show a six, then we toss a coin. Then, the sample spate of this experiment consists of
A)
13 points
done
clear
B)
18 points
done
clear
C)
10 points
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 221) The probability of getting a total of at least 6 in the simultaneously throw of three dice is
A)
\[6/108\]
done
clear
B)
\[5/27\]
done
clear
C)
\[1/24\]
done
clear
D)
\[103/108\]
done
clear
View Answer play_arrow
question_answer 222) A sample of a 4 items is drawn at a random without replacement from a lot of 10 items containing 3 defectives. If X denotes the number of defective items in the sample, then \[P(0<X<3)\] is equal to
A)
\[3/10\]
done
clear
B)
\[4/5\]
done
clear
C)
\[1/2\]
done
clear
D)
\[1/6\]
done
clear
View Answer play_arrow
question_answer 223) Two cards are drawn successfully with replacement from a well shuffled deck of 52 cards, then the mean of the number of aces is
A)
\[1/13\]
done
clear
B)
\[3/13\]
done
clear
C)
\[2/13\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 224) An um contains 4 white and 3 red balls. Three balls are drawn with replacement from this um. Then, the standard deviation of the number of red balls drawn is
A)
\[6/7\]
done
clear
B)
\[36/49\]
done
clear
C)
\[5/7\]
done
clear
D)
\[25/49\]
done
clear
View Answer play_arrow
question_answer 225) A and B are two independent events such that \[P(A)=1/2\] and \[P(A)=1/2\] then P (neither A nor B) is equal to
A)
\[2/3\]
done
clear
B)
\[1/6\]
done
clear
C)
\[5/6\]
done
clear
D)
\[1/3\]
done
clear
View Answer play_arrow