question_answer 1) A solid cylinder is rolling down on an inclined plane of angle \[\theta ,\] The coefficient of static friction between the plane and cylinder is \[{{\mu }_{s}}\]. Then condition for the cylinder not to slip is
A)
\[\tan \,\,\theta \ge \,3{{\mu }_{s}}\]
done
clear
B)
\[\tan \,\,\theta >3{{\mu }_{s}}\]
done
clear
C)
\[\tan \,\,\theta \le 3{{\mu }_{s}}\]
done
clear
D)
\[\tan \,\,\theta <3{{\mu }_{s}}\]
done
clear
View Answer play_arrow
question_answer 2) The moment of inertia of a circular ring of mass \[1\text{ }kg\]about an axis passing through its centre and perpendicular to its plane is \[4\text{ }kg-{{m}^{2}}\]. The diameter of the ring is
A)
\[2\,\,m\]
done
clear
B)
\[4\,\,m\]
done
clear
C)
\[5\,\,m\]
done
clear
D)
\[6\,\,m\]
done
clear
View Answer play_arrow
question_answer 3) If g is the acceleration due to gravity on the surface of earth, its value at a height equal to double the radius of earth is
A)
\[g\]
done
clear
B)
\[\frac{g}{2}\]
done
clear
C)
\[\frac{g}{3}\]
done
clear
D)
\[\frac{g}{9}\]
done
clear
View Answer play_arrow
question_answer 4) On bombardment of \[{{U}^{235}}\] by slow neutrons, \[200\text{ }MeV\] energy is released. If the power output of atomic reactor is \[1.6\text{ }MW,\] then the rate of fission will be
A)
\[5\times {{10}^{16}}/s\]
done
clear
B)
\[10\times {{10}^{16}}/s\]
done
clear
C)
\[15\times {{10}^{16}}/s\]
done
clear
D)
\[20\times {{10}^{-16}}/s\]
done
clear
View Answer play_arrow
question_answer 5) A stress of \[3.18\times {{10}^{8}}\,N-{{m}^{-2}}\] is applied to a steel rod of length 1 m along its length. Its Young's modulus is \[2\times {{10}^{11}}\text{ }N-{{m}^{-2}}\]. Then, the elongation produced in the rod (in mm) is
A)
\[3.18\]
done
clear
B)
\[6.36\]
done
clear
C)
\[5.18\]
done
clear
D)
\[1.59\]
done
clear
View Answer play_arrow
question_answer 6) A liquid is allowed into a tube of truncated cone shape. Identify the correct statement from the following.
A)
The speed is high at the wider end and low at the narrow end
done
clear
B)
The speed is low at the wider end and high at the narrow end
done
clear
C)
The speed is same at both ends in a stream line flow
done
clear
D)
The liquid flows with uniform velocity in the tube
done
clear
View Answer play_arrow
question_answer 7) A sphere of radius R is gently dropped into liquid of viscosity \[\eta \] in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2R when dropped into the same liquid, will attain its terminal velocity
A)
\[v\]
done
clear
B)
\[2v\]
done
clear
C)
\[4v\]
done
clear
D)
\[9v\]
done
clear
View Answer play_arrow
question_answer 8) The excess pressure in a bubble of radius R of a gas in a liquid of surface tension S is
A)
\[\frac{2\,S}{R}\]
done
clear
B)
\[\frac{2\,R}{S}\]
done
clear
C)
\[\frac{2\,S}{{{R}^{2}}}\]
done
clear
D)
\[\frac{2{{R}^{2}}}{S}\]
done
clear
View Answer play_arrow
question_answer 9) The average kinetic energy of a gas molecule is
A)
proportional to pressure of gas
done
clear
B)
inversely proportional to volume of gas
done
clear
C)
inversely proportional to absolute temperature of gas
done
clear
D)
directly proportional to absolute temperature of gas
done
clear
View Answer play_arrow
question_answer 10) Ideal gas undergoes an adiabatic change in its state from \[({{p}_{1}},{{V}_{1}},{{T}_{1}})\] to \[({{p}_{2}},{{V}_{2}},{{T}_{2}})\]. The work done (W) in the process is (\[\mu =\] number of molecules, \[{{C}_{P}}\] and \[{{C}_{V}}\] are molar specific heats of gas)
A)
\[W=\mu {{C}_{P}}({{T}_{1}}-{{T}_{2}})\]
done
clear
B)
\[W=\mu {{C}_{V}}({{T}_{1}}-{{T}_{2}})\]
done
clear
C)
\[W=\mu {{C}_{P}}({{T}_{1}}+{{T}_{2}})\]
done
clear
D)
\[W=\mu {{C}_{V}}({{T}_{1}}+{{T}_{2}})\]
done
clear
View Answer play_arrow
question_answer 11) For an ideal gas
A)
\[{{C}_{P}}\] is less than \[{{C}_{V}}\]
done
clear
B)
\[{{C}_{P}}\] is equal to \[{{C}_{V}}\]
done
clear
C)
\[{{C}_{P}}\] is greater than \[{{C}_{V}}\]
done
clear
D)
\[{{C}_{P}}={{C}_{V}}=0\]
done
clear
View Answer play_arrow
question_answer 12) For a gas molecule with 6 degrees of freedom the law of equipartition of energy gives the following relation between the molecular specific heat \[({{C}_{V}})\] and gas constant (R)
A)
\[{{C}_{V}}=\frac{R}{2}\]
done
clear
B)
\[{{C}_{V}}=R\]
done
clear
C)
\[{{C}_{V}}=2R\]
done
clear
D)
\[{{C}_{V}}=3R\]
done
clear
View Answer play_arrow
question_answer 13) Wien's displacement law for emission of radiation can be written as
A)
\[{{\lambda }_{\max }}\]max is proportional to absolute temperature (T)
done
clear
B)
\[{{\lambda }_{\max }}\] is proportional to square of absolute temperature \[({{T}^{2}})\]
done
clear
C)
\[{{\lambda }_{\max }}\] is inversely proportional to absolute temperature (T)
done
clear
D)
\[{{\lambda }_{\max }}\] is inversely proportional to square of absolute temperature \[({{T}^{2}})\] (\[{{\lambda }_{\max }}\] = wavelength whose energy density is greatest)
done
clear
View Answer play_arrow
question_answer 14) The frequency of the fundamental note in a wire stretched under tension T is /. If the tension is increased to 25 T, then the frequency of the fundamental note will be
A)
\[25\,f\]
done
clear
B)
\[5\,f\]
done
clear
C)
\[10\,f\]
done
clear
D)
\[f\]
done
clear
View Answer play_arrow
question_answer 15) The frequency of fundamental note in an organ pipe is \[240\text{ }Hz.\] On blowing air, frequencies \[720\text{ }Hz\]and \[1200\text{ }Hz\]are heard. This indicates that organ pipe is
A)
a pipe closed at one end
done
clear
B)
a pipe open at both ends
done
clear
C)
closed at both ends
done
clear
D)
having holes like flute
done
clear
View Answer play_arrow
question_answer 16) If \[{{L}_{1}}\]and \[{{L}_{2}}\] are the lengths of the first and second resonating air columns in a resonance tube, then the wavelength of the note produced is
A)
\[2({{L}_{2}}+{{L}_{1}})\]
done
clear
B)
\[2({{L}_{2}}-{{L}_{1}})\]
done
clear
C)
\[2\left( {{L}_{2}}-\frac{{{L}_{1}}}{2} \right)\]
done
clear
D)
\[2\left( {{L}_{2}}+\frac{{{L}_{1}}}{2} \right)\]
done
clear
View Answer play_arrow
question_answer 17) Beats are produced by frequencies \[{{f}_{1}}\] and \[{{f}_{2}}({{f}_{1}}>{{f}_{2}})\]. The duration of time between two successive maxima or minima is equal to
A)
\[\frac{1}{{{f}_{1}}+{{f}_{2}}}\]
done
clear
B)
\[\frac{2}{{{f}_{1}}-{{f}_{2}}}\]
done
clear
C)
\[\frac{2}{{{f}_{1}}+{{f}_{2}}}\]
done
clear
D)
\[\frac{1}{{{f}_{1}}-{{f}_{2}}}\]
done
clear
View Answer play_arrow
question_answer 18) If a body is executing simple harmonic motion, then
A)
at extreme positions, the total energy is zero
done
clear
B)
at equilibrium position, the total energy is in the form of potential energy
done
clear
C)
at equilibrium position, the total energy is in the form of kinetic energy
done
clear
D)
at extreme position, the total energy is infinite
done
clear
View Answer play_arrow
question_answer 19) An electric dipole has a pair of equal and opposite point charges q and \[-q\] separated by a distance 2x. The axis of the dipole is defined as
A)
direction from positive, charge to negative charge
done
clear
B)
direction from negative charge to positive charge
done
clear
C)
perpendicular to the line joining the two charges drawn at the centre and pointing upward direction
done
clear
D)
perpendicular to the line joining the two charges drawn at the centre and pointing downward direction
done
clear
View Answer play_arrow
question_answer 20) The dipole moment of a dipole in an uniform external field \[\vec{E}\] is \[\vec{P}\]. Then, the torque \[(\tau )\] acting on the dipole is
A)
\[\vec{\tau }=\vec{P}\times \vec{E}\]
done
clear
B)
\[\vec{\tau }=\vec{P}.\vec{E}\]
done
clear
C)
\[\vec{\tau }=2(\vec{P}+\vec{E})\]
done
clear
D)
\[\vec{\tau }=(\vec{P}+\vec{E})\]
done
clear
View Answer play_arrow
question_answer 21) The electric flux through a closed surface area S enclosing charge Q is \[\phi \]. If the surface area is doubled, then the flux is
A)
\[2\,\phi \]
done
clear
B)
\[\phi /2\]
done
clear
C)
\[\phi /4\]
done
clear
D)
\[\phi \]
done
clear
View Answer play_arrow
question_answer 22) Consider a thin spherical shell of radius R consisting of uniform surface charge density \[\sigma \] The electric field at a point of distance x from its centre and outside the shell is
A)
inversely proportional to \[\sigma \]
done
clear
B)
directly proportional to \[{{x}^{2}}\]
done
clear
C)
directly proportional to \[\sigma \]
done
clear
D)
inversely proportional to \[{{x}^{2}}\]
done
clear
View Answer play_arrow
question_answer 23) The work done in bringing at a unit positive charge from infinity distance to a point at distance X from a positive charge Q is W. Then the potential \[\phi \] at that point is
A)
\[\frac{WQ}{X}\]
done
clear
B)
\[W\]
done
clear
C)
\[\frac{W}{Q}\]
done
clear
D)
\[WQ\]
done
clear
View Answer play_arrow
question_answer 24) The capacitance C of a capacitor is
A)
independent of the charge and potential of the capacitor
done
clear
B)
dependent on the charge and independent of potential
done
clear
C)
independent of the geometrical configuration of the capacitor
done
clear
D)
independent of the dielectric medium between the two conducting surfaces of the capacitor
done
clear
View Answer play_arrow
question_answer 25)
Four capacitors are connected in a circuit as shown in the following figure. Calculate the effective capacitance between the points A and B.
A)
\[\frac{4}{3}\mu F\]
done
clear
B)
\[\frac{24}{5}\mu F\]
done
clear
C)
\[9\,\mu F\]
done
clear
D)
\[5\,\mu F\]
done
clear
View Answer play_arrow
question_answer 26) Metals have
A)
zero resistivity
done
clear
B)
high resistivity
done
clear
C)
low resistivity
done
clear
D)
infinite resistivity
done
clear
View Answer play_arrow
question_answer 27) The electric potential inside a conducting sphere
A)
increases from centre to surface
done
clear
B)
decreases from centre to surface
done
clear
C)
remains constant from centre to surface
done
clear
D)
is zero at every point inside
done
clear
View Answer play_arrow
question_answer 28) Electron of mass m and charge e in external field £ experiences acceleration
A)
\[\frac{e}{mE},\] in the opposite direction to the field
done
clear
B)
\[\frac{eE}{m},\] in the direction of the field
done
clear
C)
\[\frac{em}{E},\] m the direction of the field
done
clear
D)
\[\frac{eE}{m},\] in the opposite direction of the field,
done
clear
View Answer play_arrow
question_answer 29) Kirchhoff?s second law for the analysis of circuit is based on
A)
conservation of charge
done
clear
B)
conservation of energy
done
clear
C)
conservation of both charge and energy
done
clear
D)
conservation of momentum of electron
done
clear
View Answer play_arrow
question_answer 30)
In circuit shown below, the resistances are given in ohm and the battery is assumed ideal with emf equal to\[3\text{ }V\]. The voltage across the resistance \[{{R}_{4}}\] is
A)
\[0.4V\]
done
clear
B)
\[0.6V\]
done
clear
C)
\[1.2\text{ }V\]
done
clear
D)
\[1.5V\]
done
clear
View Answer play_arrow
question_answer 31) The direction of induced magnetic field \[d\,\,\vec{B}\] due to current element i d \[\vec{L},\] at a point of distance r from it, when a current i passes through a long conductor is in the direction
A)
of position vector \[\vec{r}\] of the point
done
clear
B)
of current element \[d\,\vec{L}\]
done
clear
C)
perpendicular to both \[d\,\vec{L}\] and \[\vec{r}\]
done
clear
D)
perpendicular to \[\vec{L}\] only
done
clear
View Answer play_arrow
question_answer 32) The magnetic force on a charged particle moving in the field does not work, because
A)
kinetic energy of the charged particle does not change
done
clear
B)
the charge of the particle remains same
done
clear
C)
the magnetic force is parallel to velocity of the particle
done
clear
D)
the magnetic force is parallel to magnetic field
done
clear
View Answer play_arrow
question_answer 33) To convert a moving coil galvanometer (MCG) into a voltmeter
A)
a high resistance R is connected in parallel with MCG
done
clear
B)
a low resistance r is connected in parallel with MCG
done
clear
C)
a low resistance r is connected in series With MCG
done
clear
D)
a high resistance R is connected in series with MCG
done
clear
View Answer play_arrow
question_answer 34) Identify the correct statement from the following.
A)
Cyclotron frequency is dependent on speed of the charged particle
done
clear
B)
Kinetic energy of charged particle in cyclotron does not dependent on its mass
done
clear
C)
Cyclotron frequency does not depend on speed of charged particle
done
clear
D)
Kinetic energy of charged particle in cyclotron is independent of its charge
done
clear
View Answer play_arrow
question_answer 35) Consider two straight parallel conductors A and B separated by a distance x and carrying individual currents \[{{i}_{A}}\] and \[{{i}_{B}}\] respectively. If the two conductors attract each other, it indicates that
A)
the two currents are parallel in direction
done
clear
B)
the two currents are anti-parallel in direction
done
clear
C)
the magnetic lines of induction are parallel
done
clear
D)
the magnetic lines of induction are parallel to length of conductors
done
clear
View Answer play_arrow
question_answer 36) The magnetic susceptibility of paramagnetic materials is
A)
positive, but very high
done
clear
B)
negative, but small
done
clear
C)
negative but very high
done
clear
D)
positive, but small
done
clear
View Answer play_arrow
question_answer 37) According to Lenz's law of electromagnetic induction
A)
the induced emf is not in the direction opposing the change in magnetic flux
done
clear
B)
the relative motion between the coil and magnet produces change in magnetic flux
done
clear
C)
only the magnet should be moved towards coil
done
clear
D)
only the coil should be moved towards magnet
done
clear
View Answer play_arrow
question_answer 38) According to phenomenon of mutual inductance
A)
the mutual inductance does not dependent on geometry of the two coils involved
done
clear
B)
the mutual inductance depends on the intrinsic magnetic property, like relative permeability of the material
done
clear
C)
the mutual inductance is independent of the magnetic property of the material
done
clear
D)
ratio of magnetic flux produced by the coil 1 at-the place of the coil 2 and the current in the coil 2 will be different from that of the ratio defined by interchanging the coils
done
clear
View Answer play_arrow
question_answer 39) The natural frequency \[({{\omega }_{0}})\] of oscillations in L-C circuit is given by
A)
\[\frac{1}{2\pi }\frac{1}{\sqrt{LC}}\]
done
clear
B)
\[\frac{1}{2\pi }\,\sqrt{LC}\]
done
clear
C)
\[\frac{1}{\,\sqrt{LC}}\]
done
clear
D)
\[\sqrt{LC}\]
done
clear
View Answer play_arrow
question_answer 40) In L-C-R series circuit the resonance condition in terms of capacitive reactance \[({{X}_{C}})\] and inductive reactance \[({{X}_{L}})\] is
A)
\[{{X}_{C}}+{{X}_{L}}=0\]
done
clear
B)
\[{{X}_{C}}=0\]
done
clear
C)
\[{{X}_{L}}=0\]
done
clear
D)
\[{{X}_{C}}-{{X}_{L}}=0\]
done
clear
View Answer play_arrow
question_answer 41) In step-up transformer, relation between number of turns in primary \[({{N}_{P}})\] and number of turns in secondary \[({{N}_{S}})\] coils is
A)
\[{{N}_{s}}\] is greater than \[{{N}_{p}}\]
done
clear
B)
\[{{N}_{p}}\] is greater than \[{{N}_{s}}\]
done
clear
C)
\[{{N}_{s}}\] is equal to \[{{N}_{p}}\]
done
clear
D)
\[{{N}_{p}}=2{{N}_{s}}\]
done
clear
View Answer play_arrow
question_answer 42) Two light sources are said to be of coherent nature
A)
when they have same frequency and a varying phase difference
done
clear
B)
when they have same frequency and a constant phase difference
done
clear
C)
when they have constant phase difference and different frequencies
done
clear
D)
when they have varying phase difference and different frequencies
done
clear
View Answer play_arrow
question_answer 43) In Young's double slit interference pattern the fringe width
A)
can be changed only by changing the wavelength of incident light
done
clear
B)
can be changed only by changing the separation between the two slits
done
clear
C)
can be changed either by changing the wavelength or by changing the separation between two sources
done
clear
D)
is a universal constant and hence cannot be changed
done
clear
View Answer play_arrow
question_answer 44) Colours in thin films are due to
A)
diffraction phenomenon
done
clear
B)
scattering phenomenon
done
clear
C)
interference phenomenon
done
clear
D)
polarization phenomenon
done
clear
View Answer play_arrow
question_answer 45) Brewster?s angle in terms of refractive index (n) of the medium
A)
\[{{\tan }^{-1}}\,\sqrt{n}\]
done
clear
B)
\[{{\sin }^{-1}}\,n\]
done
clear
C)
\[{{\sin }^{-1}}\,\sqrt{n}\]
done
clear
D)
\[{{\tan }^{-1}}\,n\]
done
clear
View Answer play_arrow
question_answer 46)
The angle of incidence of light is equal to Brewster?s angle, then A. reflected ray is perpendicular to refracted ray B. refracted ray is parallel to reflected ray C. reflected light is polarized having its electric vector in the plane of incidence D. refracted light is polarized
A)
[A] and [D] are true
done
clear
B)
[A] and [B] are true
done
clear
C)
[A] and [C] are true
done
clear
D)
[B] and [C] are true
done
clear
View Answer play_arrow
question_answer 47) The working of optical fibres is based on
A)
dispersion of light
done
clear
B)
total internal reflection
done
clear
C)
polarization of light
done
clear
D)
interference of light
done
clear
View Answer play_arrow
question_answer 48) First Bohr radius of an atom with \[Z=82\]is R. Radius of its third orbit is
A)
\[9\,\,R\]
done
clear
B)
\[6\,\,R\]
done
clear
C)
\[3\,R\]
done
clear
D)
\[R\]
done
clear
View Answer play_arrow
question_answer 49) The de-Broglie wavelength associated with a particle moving with momentum (p) and mass (m) is
A)
\[\frac{h}{p}\]
done
clear
B)
\[\frac{h}{mp}\]
done
clear
C)
\[\frac{h}{{{p}^{2}}}\]
done
clear
D)
\[\frac{{{h}^{2}}}{{{p}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 50) The angular momentum (L) of an electron moving in a stable orbit around nucleus is
A)
half integral multiple of \[\frac{h}{2\pi }\]
done
clear
B)
integral multiple of h
done
clear
C)
integral multiple of \[\frac{h}{2\pi }\]
done
clear
D)
half integral multiple of h
done
clear
View Answer play_arrow
question_answer 51) According to Moseley's law of X-rays the frequency (v) of a particular characteristic X-ray and the atomic number (Z) of the element depend on each other as
A)
\[\sqrt{v}=k{{Z}^{2}}\]
done
clear
B)
\[\sqrt{v}=\frac{h}{{{Z}^{2}}}\]
done
clear
C)
\[v=kZ\]
done
clear
D)
\[\sqrt{v}=kZ\]
done
clear
View Answer play_arrow
question_answer 52) If \[\lambda \] is decay constant and N the number of radioactive nuclei of an element, then the decay rate (R) of that element is
A)
\[\lambda {{N}^{2}}\]
done
clear
B)
\[\lambda N\]
done
clear
C)
\[\frac{\lambda }{N}\]
done
clear
D)
\[{{\lambda }^{2}}N\]
done
clear
View Answer play_arrow
question_answer 53) The ratio of half-life times of two elements A and B is \[\frac{{{T}_{A}}}{{{T}_{B}}}\] The ratio of respective decay constants \[\frac{{{\lambda }_{A}}}{{{\lambda }_{B}}}\] is
A)
\[\frac{{{T}_{B}}}{{{T}_{A}}}\]
done
clear
B)
\[\frac{{{T}_{A}}}{{{T}_{B}}}\]
done
clear
C)
\[\frac{{{T}_{A}}+{{T}_{B}}}{{{T}_{A}}}\]
done
clear
D)
\[\frac{{{T}_{A}}-{{T}_{B}}}{{{T}_{A}}}\]
done
clear
View Answer play_arrow
question_answer 54) For a nuclear to be in critical condition, the value of neutron multiplication factor (k) must be
A)
\[k>1\]
done
clear
B)
\[k<1\]
done
clear
C)
\[k=1\]
done
clear
D)
\[k=0\]
done
clear
View Answer play_arrow
question_answer 55) If \[{{n}_{E}}\] and \[{{n}_{H}}\] represent the number of free electrons and holes respectively in a semiconducting material, then for n-type semiconducting material
A)
\[{{n}_{E}}<<{{n}_{H}}\]
done
clear
B)
\[{{n}_{E}}>>{{n}_{H}}\]
done
clear
C)
\[{{n}_{E}}={{n}_{H}}\]
done
clear
D)
\[{{n}_{E}}={{n}_{H}}=0\]
done
clear
View Answer play_arrow
question_answer 56) An intrinsic semiconductor at \[0\text{ }K\]temperature behaves like
A)
conductor
done
clear
B)
p-type semiconductor
done
clear
C)
n-typesemiconductor
done
clear
D)
insulator
done
clear
View Answer play_arrow
question_answer 57) When a p-n junction diode is connected in forward bias its barrier potential
A)
decreases and less current flows in the circuit
done
clear
B)
decreases and more current flows in the circuit
done
clear
C)
increases and more current flows in the circuit
done
clear
D)
decreases and no current flows in the circuit
done
clear
View Answer play_arrow
question_answer 58) The main cause of zener breakdown is
A)
the base semiconductor being germanium
done
clear
B)
production of electron-hole pairs due to thermal excitation
done
clear
C)
low doping
done
clear
D)
high doping
done
clear
View Answer play_arrow
question_answer 59) The depletion layer in a silicon diode is \[1\,\mu m\] wide and its knee potential is \[0.6\text{ }V,\] then the electric field in the depletion layer will be
A)
\[0.6\text{ }V/m\]
done
clear
B)
\[6\times {{10}^{4}}\,V/m\]
done
clear
C)
\[6\times {{10}^{5}}\,V/m\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 60) Identify the true statement for OR gate
A)
Output Y will be 1 when input A or B or both are 1
done
clear
B)
Output Y will be 0 when the either of the inputs A or B is 1
done
clear
C)
Output Y will be 1 only when both the inputs A and Bare 1
done
clear
D)
Output Y will be 1 only when either of the inputs A and B are 1
done
clear
View Answer play_arrow
question_answer 61) Dimensional formula for force is
A)
\[[M{{L}^{2}}{{T}^{-2}}]\]
done
clear
B)
\[[ML{{T}^{-2}}]\]
done
clear
C)
\[[M{{L}^{-1}}{{T}^{-2}}]\]
done
clear
D)
\[[M{{L}^{2}}{{T}^{-2}}]\]
done
clear
View Answer play_arrow
question_answer 62) X is a vector with magnitude A, then the unit vector a in the direction of vector A is
A)
\[A\,\vec{A}\]
done
clear
B)
\[\vec{A}.\,\vec{A}\]
done
clear
C)
\[\vec{A}\times \,\vec{A}\]
done
clear
D)
\[\frac{|\vec{A}|}{A}\]
done
clear
View Answer play_arrow
question_answer 63) A body is under the action of two mutually perpendicular forces of \[3\text{ }N\]and\[4\text{ }N\]. The resultant force acting on the body is
A)
\[7\,N\]
done
clear
B)
\[1\,N\]
done
clear
C)
\[5\,N\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 64) If the scalar and vector products of two vectors X and S are equal in magnitude, then the angle between the two vectors is
A)
\[{{45}^{o}}\]
done
clear
B)
\[{{90}^{o}}\]
done
clear
C)
\[{{180}^{o}}\]
done
clear
D)
\[{{360}^{o}}\]
done
clear
View Answer play_arrow
question_answer 65) A body is moving along a straight line path with constant velocity. At an instant of time the distance travelled by it is 5 and its displacement is D, then
A)
\[D<s\]
done
clear
B)
\[D>s\]
done
clear
C)
\[D=s\]
done
clear
D)
\[D\le s\]
done
clear
View Answer play_arrow
question_answer 66) A body is projected at an angle \[\theta \] with respect to horizontal direction with velocity u. The maximum range of the body is
A)
\[R=\frac{{{u}^{2}}\,\sin \,\,2\theta }{g}\]
done
clear
B)
\[R=\frac{{{u}^{2}}\,{{\sin }^{2}}\theta }{2g}\]
done
clear
C)
\[R=\frac{{{u}^{2}}}{g}\]
done
clear
D)
\[R={{u}^{2}}\,\,\sin \,\,\theta \]
done
clear
View Answer play_arrow
question_answer 67) A body moving along a circular path of radius R with velocity v, has centripetal acceleration a. If its velocity is made equal to 2v, then its centripetal acceleration is
A)
\[4\,a\]
done
clear
B)
\[2\,a\]
done
clear
C)
\[\frac{a}{4}\]
done
clear
D)
\[\frac{a}{2}\]
done
clear
View Answer play_arrow
question_answer 68) A cyclist is travelling with velocity v on a banked curved road of radius R. The angle \[\theta \] through which the cyclist leans inwards is given by
A)
\[\tan \,\theta =\frac{Rg}{{{v}^{2}}}\]
done
clear
B)
\[\tan \,\theta ={{v}^{2}}\,Rg\]
done
clear
C)
\[\tan \,\theta =\frac{{{v}^{2}}\,g}{R}\]
done
clear
D)
\[\tan \,\theta =\frac{{{v}^{2}}}{Rg}\]
done
clear
View Answer play_arrow
question_answer 69) A body starts from rest and moves with uniform acceleration. Which of the following graphs represent its motion?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 70) A gun fires N bullets per second, each of mass m with velocity v. The force exerted by the bullets on the gun is
A)
\[vNm\]
done
clear
B)
\[\frac{mv}{N}\]
done
clear
C)
\[mv{{N}^{2}}\]
done
clear
D)
\[\frac{m{{v}^{2}}}{N}\]
done
clear
View Answer play_arrow
question_answer 71) The rate of mass of the gas emitted from rear of a rocket is initially\[0.1\text{ }kg/s\]. If the speed of the gas relative to the rocket is \[50\text{ }m/s\]and mass of the rocket is\[2\text{ }kg\], then the acceleration of the rocket (in\[m/{{s}^{2}}\]) is
A)
\[5\]
done
clear
B)
\[5.2\]
done
clear
C)
\[2.5\]
done
clear
D)
\[25\]
done
clear
View Answer play_arrow
question_answer 72) The area under the displacement-force curve gives
A)
distance travelled
done
clear
B)
total force
done
clear
C)
momentum
done
clear
D)
work done
done
clear
View Answer play_arrow
question_answer 73) Identify the correct statement for the rotational motion of a rigid body.
A)
Individual particles of the body do not undergo accelerated motion
done
clear
B)
The centre of mass of the body remains unchanged
done
clear
C)
The centre of mass of the body moves uniformly in a circular path
done
clear
D)
Individual particles and centre of mass the body undergo an accelerated motion
done
clear
View Answer play_arrow
question_answer 74) The moment of inertia about an axis of a body which is rotating with angular velocity 1 rad/s is numerically equal to
A)
one-fourth of its rotational kinetic energy
done
clear
B)
half of the rotational kinetic energy
done
clear
C)
rotational kinetic energy
done
clear
D)
twice the rotational kinetic energy
done
clear
View Answer play_arrow
question_answer 75) The moment of inertia of a circular disc of radius\[2\text{ }m\]and mass \[2\text{ }kg,\] about an axis passing through its centre of mass is\[2\text{ }kg-{{m}^{2}}\]. Its moment of inertia about an axis parallel to this axis and passing through its edge (in\[kg-{{m}^{2}}\]) is
A)
\[10\]
done
clear
B)
\[8\]
done
clear
C)
\[6\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 76) The phenomenon observed when a beam of light is passed through a colloidal solution, is
A)
cataphoresis
done
clear
B)
delectrophoresis
done
clear
C)
coagulation
done
clear
D)
Tyndall effect
done
clear
View Answer play_arrow
question_answer 77) In case of condensation of polymers
A)
high molecular weight polymers are formed all at once
done
clear
B)
lower molecular weight polymers are formed all at once
done
clear
C)
molecular weight of polymer rises throughout the reaction
done
clear
D)
have no Specific relation to their molecular weight
done
clear
View Answer play_arrow
question_answer 78) The element with the lowest ionization potential is
A)
Na
done
clear
B)
K
done
clear
C)
Rb
done
clear
D)
Cs
done
clear
View Answer play_arrow
question_answer 79) Differentiating electron in inner transition elements enters the ......... orbital.
A)
s
done
clear
B)
p
done
clear
C)
d
done
clear
D)
\[f\]
done
clear
View Answer play_arrow
question_answer 80) Which one of the following is a non-polar molecule?
A)
\[CC{{l}_{4}}\]
done
clear
B)
\[CHC{{l}_{3}}\]
done
clear
C)
\[C{{H}_{2}}C{{l}_{2}}\]
done
clear
D)
\[C{{H}_{3}}Cl\]
done
clear
View Answer play_arrow
question_answer 81) The nature of the bond in diamond is
A)
ionic
done
clear
B)
covalent
done
clear
C)
metallic
done
clear
D)
coordinate covalent
done
clear
View Answer play_arrow
question_answer 82) According to VSEPR theory the repulsion between different pair (lone or bond) of electrons obey the order
A)
\[lp-bp-lp-lp>bp-bp\]
done
clear
B)
\[lp-bp>bp-bp>lp-lp\]
done
clear
C)
\[lp-lp>lp-bp>lp-bp\]
done
clear
D)
\[bp-bp>lp-lp>lp-bp\]
done
clear
View Answer play_arrow
question_answer 83) From the molecular orbital theory, one can show that the bond order in \[{{F}_{2}}\]molecule as
A)
2
done
clear
B)
1
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 84) Which of the following metal oxides is most basic?
A)
\[ZnO\]
done
clear
B)
\[~A{{l}_{2}}{{O}_{3}}\]
done
clear
C)
\[A{{s}_{2}}{{O}_{3}}\]
done
clear
D)
\[{{K}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 85) In the laboratory \[{{\text{H}}_{\text{2}}}\text{S}\]gas is prepared by using black lumps and dil.\[{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\text{.}\] The black lumps are
A)
\[~FeS{{O}_{4}}\]
done
clear
B)
\[~Mn{{O}_{2}}\]
done
clear
C)
\[FeS\]
done
clear
D)
\[FeS{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 86) The order of electron affinity of halogens is
A)
\[F>Cl>Br>I\]
done
clear
B)
\[Cl>F>Br>I\]
done
clear
C)
\[Cl>F>I>Br\]
done
clear
D)
\[Br>Cl>F>I\]
done
clear
View Answer play_arrow
question_answer 87) When chlorine reacts with dil. \[\text{NaOH}\]under cold conditions, the oxidation state of chlorine changes from zero to
A)
- 1 and + 5
done
clear
B)
+ 1 and + 4
done
clear
C)
+ 5 and +3
done
clear
D)
- 1 and + 1
done
clear
View Answer play_arrow
question_answer 88) The highest oxidation state exhibited by transition metals is
A)
+ 7
done
clear
B)
+ 8
done
clear
C)
+ 6
done
clear
D)
+ 5
done
clear
View Answer play_arrow
question_answer 89) Which one of the following statements is not true with regard to transition elements?
A)
They readily form complex compounds
done
clear
B)
They show variable oxidation states
done
clear
C)
All their ions are colourless
done
clear
D)
Their ions contain partially filled d-electrons
done
clear
View Answer play_arrow
question_answer 90) The catalyst used in the manufacture of ammonia is
A)
\[{{V}_{2}}{{O}_{5}}\]
done
clear
B)
\[Pt\]
done
clear
C)
\[Fe\]
done
clear
D)
\[Ni{{(CO)}_{4}}\]
done
clear
View Answer play_arrow
question_answer 91) The most stable oxidation state of lanthanides is
A)
+ 2
done
clear
B)
+ 4
done
clear
C)
0
done
clear
D)
+ 3
done
clear
View Answer play_arrow
question_answer 92) The number of ions formed when hexamine copper (II) sulphate is dissolved in water is
A)
1
done
clear
B)
2
done
clear
C)
4
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 93) The number of unpaired electrons in the square planar \[{{[Pt{{(CN)}_{4}}]}^{2-}}\]ion is
A)
2
done
clear
B)
1
done
clear
C)
0
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 94) In metal carbonyl (organometallic) complexes, the M-C bond is
A)
ionic
done
clear
B)
covalent with ionic character
done
clear
C)
covalent
done
clear
D)
coordinate covalent
done
clear
View Answer play_arrow
question_answer 95) The complexes\[[PrC{{l}_{2}}{{(N{{H}_{3}})}_{4}}]B{{r}_{2}}\] and \[[PtB{{r}_{2}}{{(N{{H}_{3}})}_{4}}]C{{l}_{2}}\]are examples for isomerism
A)
geometrical
done
clear
B)
optical
done
clear
C)
ionisation
done
clear
D)
linkage
done
clear
View Answer play_arrow
question_answer 96) The metallurgical process in which a metal is obtained in a fused state is called
A)
smelting
done
clear
B)
roasting
done
clear
C)
calcination
done
clear
D)
froth floatation
done
clear
View Answer play_arrow
question_answer 97) Metallic silver may be obtained from \[\text{AgCl}\]by
A)
heating it in the current of \[{{\text{H}}_{\text{2}}}\]
done
clear
B)
fusing it with sand
done
clear
C)
treating with carbon monoxide
done
clear
D)
fusing it with \[\text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}\]
done
clear
View Answer play_arrow
question_answer 98) Which one of the following metals is extracted by a carbon reduction process?
A)
Copper
done
clear
B)
Iron
done
clear
C)
Aluminium
done
clear
D)
Magnesium
done
clear
View Answer play_arrow
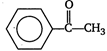
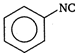
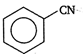
question_answer 99) IUPAC name of \[C{{H}_{3}}-\underset{Cl}{\mathop{\underset{|}{\mathop{C}}\,}}\,H-C{{H}_{2}}-CHO\]is \[Cl\]
A)
3-chlorobutanol
done
clear
B)
3-chlorobutanaldehyde
done
clear
C)
3-chlorobutanal
done
clear
D)
2-chlorobutanol
done
clear
View Answer play_arrow
question_answer 100) Di-chloroacetic acid is a stronger acid than acetic acid. This is due to occurrence of
A)
mesomeric effect
done
clear
B)
hyperconjugation
done
clear
C)
inductive effect
done
clear
D)
steric effect
done
clear
View Answer play_arrow
question_answer 101) Dehydration of alcohol is an example of which type of reaction?
A)
Substitution
done
clear
B)
Elimination
done
clear
C)
Addition
done
clear
D)
Rearrangement
done
clear
View Answer play_arrow
question_answer 102) Number of monochloro derivatives obtained when neo-pentane is chlorinated, is
A)
one
done
clear
B)
two
done
clear
C)
three
done
clear
D)
four
done
clear
View Answer play_arrow
question_answer 103) Which of the following alkenes gives only acetaldehyde on ozonolysis?
A)
Ethene
done
clear
B)
Propene
done
clear
C)
1-butene
done
clear
D)
2-butene
done
clear
View Answer play_arrow
question_answer 104) 1-butyne on hydration gives
A)
butan-1, 2-diol
done
clear
B)
butan-1-ol
done
clear
C)
butan-2-ol
done
clear
D)
butan-2-one
done
clear
View Answer play_arrow
question_answer 105) Least stable conformer of cyclohexane is
A)
chair
done
clear
B)
boat
done
clear
C)
twist boat
done
clear
D)
planar hexagon
done
clear
View Answer play_arrow
question_answer 106) Which one of the following monoenes does not exhibit geometric isomerism?
A)
\[{{C}_{4}}{{H}_{8}}\]
done
clear
B)
\[{{C}_{3}}{{H}_{6}}\]
done
clear
C)
\[{{C}_{5}}{{H}_{10}}\]
done
clear
D)
\[{{C}_{8}}{{H}_{16}}\]
done
clear
View Answer play_arrow
question_answer 107) Which one of the following chlorohydrocarbons readily undergoes solvolysis?
A)
\[C{{H}_{2}}=CHCl\]
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 108) Conversion of chlorobenzene to phenol involves
A)
electrophilic substitution
done
clear
B)
nucleophilic substitution
done
clear
C)
free radical substituion
done
clear
D)
electrophilic addition
done
clear
View Answer play_arrow
question_answer 109)
A)
an ester
done
clear
B)
an anhydride
done
clear
C)
acetal
done
clear
D)
hemiacetal
done
clear
View Answer play_arrow
question_answer 110) Which one of the following does not give iodoform?
A)
done
clear
B)
\[C{{H}_{3}}OH\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
D)
\[C{{H}_{3}}-\underset{OH}{\mathop{\underset{|}{\mathop{C}}\,}}\,H-C{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 111) The products obtained when anisole is heated in a sealed tube with HI are
A)
done
clear
B)
done
clear
C)
done
clear
D)
\[C{{H}_{3}}OH+C{{H}_{3}}I\]
done
clear
View Answer play_arrow
question_answer 112) Which of the following diacid readily gives anhydride on heating?
A)
Fumaric
done
clear
B)
Maleic acid
done
clear
C)
Malic acid
done
clear
D)
Terephthalic acid
done
clear
View Answer play_arrow
question_answer 113) Hydroxamic acid test is employed to detect
A)
ketones
done
clear
B)
aldehydes
done
clear
C)
esters
done
clear
D)
amides
done
clear
View Answer play_arrow
question_answer 114) Picric acid is a stronger acid than acetic acid and benzoic acid. It contains
A)
\[-\text{S}{{\text{O}}_{\text{3}}}\text{H}\]group
done
clear
B)
two\[-COOH\] groups
done
clear
C)
phenolic group
done
clear
D)
three \[-COOH\]groups
done
clear
View Answer play_arrow
question_answer 115) Benzamide can be converted into benzonitrile with
A)
\[{{H}_{3}}{{O}^{+}}\]
done
clear
B)
\[O{{H}^{-}}/{{H}_{2}}O\]
done
clear
C)
KCN
done
clear
D)
\[{{P}_{2}}{{O}_{5}}\]
done
clear
View Answer play_arrow
question_answer 116) The most basic compound in the following is
A)
\[N{{H}_{3}}\]
done
clear
B)
\[~C{{H}_{3}}N{{H}_{2}}\]
done
clear
C)
\[HN{{(C{{H}_{3}})}_{2}}\]
done
clear
D)
\[N{{(C{{H}_{3}})}_{3}}\]
done
clear
View Answer play_arrow
question_answer 117) The compound with foul odour among the following is-
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
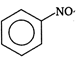
question_answer 118) Nitration of nitrobenzene at \[125{}^\circ C\] with mixed acids gives
A)
meto-dinitrobenzene
done
clear
B)
ortho-dinitrobenzene
done
clear
C)
para-dinitrobenzene
done
clear
D)
1, 3, 5-trinitro benzene
done
clear
View Answer play_arrow
question_answer 119) The \[\alpha -\]amino acid which does not give purple colour in the ninhydrin test is
A)
proline
done
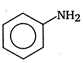
clear
B)
glycine
done
clear
C)
lysine
done
clear
D)
aspartic acid
done
clear
View Answer play_arrow
question_answer 120) The anomeric carbon in \[\text{D}\,\text{(+)}\]glucose is
A)
\[C-1\]carbon
done
clear
B)
\[C-2\]carbon
done
clear
C)
\[C-5\]carbon
done
clear
D)
\[C-6\] carbon
done
clear
View Answer play_arrow
question_answer 121) The stoichiometry of the following reaction is \[{{K}_{2}}{{S}_{2}}{{O}_{8}}(aq)+2KI(aq)\to 2{{K}_{2}}S{{O}_{4}}(aq)+{{I}_{2}}(aq)\]
A)
2:2
done
clear
B)
1:1
done
clear
C)
1:2
done
clear
D)
2:1
done
clear
View Answer play_arrow
question_answer 122) Of two oxides of iron, the first contained 22% and the second contained 30% of oxygen by weight. The ratio of weights of iron in the two oxides that combine with the same weight of oxygen, is
A)
3:2
done
clear
B)
2:1
done
clear
C)
1:2
done
clear
D)
1:1
done
clear
View Answer play_arrow
question_answer 123) The scientist who proposed the atomic model based on the quantization of energy for the first time is
A)
Max Planck
done
clear
B)
Niels Bohr
done
clear
C)
de-Broglie
done
clear
D)
Heisenberg
done
clear
View Answer play_arrow
question_answer 124) Which one of the following is the set of correct quantum numbers of an electron in 3d orbital?
A)
\[~n=3,l=0,m=0,s=-\text{ }1/2\]
done
clear
B)
\[~n=2,l=3,m=0,s=+1/2\]
done
clear
C)
\[~n=3,l=1,m=0,s=-1/2\]
done
clear
D)
\[~n=3,l=2,m=1,s=+\,1/2\]
done
clear
View Answer play_arrow
question_answer 125) Electron density in the YZ plane of \[3{{d}_{{{x}^{2}}-{{y}^{2}}}}\] orbital is
A)
zero
done
clear
B)
0.50
done
clear
C)
0.75
done
clear
D)
0.90
done
clear
View Answer play_arrow
question_answer 126) The half-life period of a radioactive isotope is 4.8 min. Starting with 1 mg of the isotope, how much of it would remain after 10 min?
A)
0.5 mg
done
clear
B)
0.726 mg
done
clear
C)
0.126 mg
done
clear
D)
0.236 mg
done
clear
View Answer play_arrow
question_answer 127) The number of beta particles emitted in the radioactive decay series from \[^{238}{{U}_{92}}\]to \[^{206}P{{b}_{82}}\]is
A)
10
done
clear
B)
8
done
clear
C)
6
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 128) What happens to the yield on application of high pressure in the Habefs synthesis of ammonia?
A)
Increases
done
clear
B)
Decreases
done
clear
C)
Unaffected
done
clear
D)
Reaction stops
done
clear
View Answer play_arrow
question_answer 129) In the reaction\[{{H}_{2}}(g)+C{{l}_{2}}(g)\rightleftharpoons 2HCl(g)\]
A)
\[{{K}_{p}}\ne {{K}_{c}}\]
done
clear
B)
\[{{K}_{p}}={{K}_{c}}\]
done
clear
C)
\[{{K}_{p}}>{{K}_{c}}\]
done
clear
D)
\[{{K}_{p}}<{{K}_{c}}\]
done
clear
View Answer play_arrow
question_answer 130) pH of an aqueous solution containing \[{{10}^{-8}}mol/L\]of \[HCl\]is
A)
8
done
clear
B)
10
done
clear
C)
6.96
done
clear
D)
12
done
clear
View Answer play_arrow
question_answer 131) An aqueous solution contains \[N{{i}^{2+}},C{{o}^{2+}}\]and\[P{{b}^{2+}}\]ions at equal concentrations. The solubility product of \[\text{NiS, PbS}\]and \[\text{CoS}\]in water at \[\text{25}{{\,}^{\text{o}}}\text{C}\]are \[\text{1}\text{.4}\times \text{1}{{\text{0}}^{-24}},\]and\[3\times {{10}^{-26}},\]respectively. Indicate which of these ions will be precipitated first and last when sulphide concentration is progressively increased from zero?
A)
NiS and PbS
done
clear
B)
NiS and CoS
done
clear
C)
CoS and NiS
done
clear
D)
PbS and NiS
done
clear
View Answer play_arrow
question_answer 132) A reaction involving A, B and C as reactants is found to obey the rate law, rate \[=k{{[A]}^{x}}{{[B]}^{y}}{{[C]}^{z}}.\]When the concentrations of A, B and C are doubled separately, the rate is also found to increase two, zero and four times respectively. The overall order of the reaction is
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 133) The units of the rate of a second order reaction are
A)
\[\text{tim}{{\text{e}}^{-1}}\]
done
clear
B)
\[\text{mol}\,{{\text{L}}^{-1}}\,\text{tim}{{\text{e}}^{-1}}\]
done
clear
C)
\[\text{L}\,\text{mol}{{\,}^{-1}}\,\text{tim}{{\text{e}}^{-1}}\]
done
clear
D)
\[{{\text{L}}^{2}}\,\text{mol}{{\,}^{-2}}\,\text{tim}{{\text{e}}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 134) Activation energy of a reaction
A)
is independent of temperature
done
clear
B)
increases with temperature
done
clear
C)
gets doubled for every 10 degree rise in temperature
done
clear
D)
decreases with temperature
done
clear
View Answer play_arrow
question_answer 135) Which one of the following concentration units is independent of temperature?
A)
Normality
done
clear
B)
Molarity
done
clear
C)
Molality
done
clear
D)
ppm
done
clear
View Answer play_arrow
question_answer 136) Maximum lowering of vapour pressure is observed in the case of
A)
0.1 M glucose
done
clear
B)
\[0.1\text{ }M\text{ }BaC{{l}_{2}}\]
done
clear
C)
\[\text{ }\!\!~\!\!\text{ 0}\text{.1 M MgS}{{\text{O}}_{\text{4}}}\]
done
clear
D)
\[\text{ }\!\!~\!\!\text{ 0}\text{.1 NaCl}\]
done
clear
View Answer play_arrow
question_answer 137) A solution containing 4 g of polyvinyl chloride polymer in one litre of dioxane was found to have an osmotic pressure of \[\text{4}\text{.1}\times {{10}^{-4}}\text{atm}\]at \[\text{27}{{\,}^{\text{o}}}\text{C}\text{.}\] The approximate molecular weight of the polymer is
A)
1500
done
clear
B)
10,000
done
clear
C)
\[\text{2}\text{.4}\times \text{1}{{\text{0}}^{5}}\]
done
clear
D)
\[\text{2}\times \text{1}{{\text{0}}^{12}}\]
done
clear
View Answer play_arrow
question_answer 138) Abnormal colligative properties are observed only when the dissolved non-volatile solute in a given dilute solution
A)
is a non-electrolyte
done
clear
B)
offers an intense colour
done
clear
C)
associates or dissociates
done
clear
D)
offers no colour
done
clear
View Answer play_arrow
question_answer 139) We believe in the laws of thermodynamics because they are
A)
theoretical
done
clear
B)
derived based on mathematical analysis
done
clear
C)
empirical and nobody disproved
done
clear
D)
mere statements
done
clear
View Answer play_arrow
question_answer 140) The latent heat of fusion of ice at \[0{{\,}^{o}}C\]is\[\text{80}\,\text{cal/g}\text{.}\]Entropy change \[\text{(}\Delta S\text{)}\] accompanying the melting of 1 g of ice at \[0{{\,}^{o}}C\]would be (units:\[cal/g/K\])
A)
273
done
clear
B)
8.0
done
clear
C)
0.0
done
clear
D)
0.293
done
clear
View Answer play_arrow
question_answer 141) \[\Delta H\] for the reaction, \[C(graphite)+2{{H}_{2}}(g)\xrightarrow{{}}C{{H}_{4}}(g)\]at \[298\,K\]and 1 atm is\[~-\text{ }17900\text{ cal}\text{.}\] The \[\Delta E\]for the above conversion would be
A)
\[-\text{ }17900\text{ cal}\]
done
clear
B)
\[\text{ }\!\!~\!\!\text{ 17900 cal}\]
done
clear
C)
\[\text{17308 cal}\]
done
clear
D)
\[~-\text{ }17308\text{ cal}\]
done
clear
View Answer play_arrow
question_answer 142) Which one of the following is spontaneous at all temperatures?
A)
\[{{H}_{2}}(g)\xrightarrow{{}}2{{H}_{\text{atom}}}\] \[\Delta {{H}^{o}}=436\,kJ,\Delta {{S}^{o}}=90.7\,\text{eu}\]
done
clear
B)
\[\frac{1}{2}{{N}_{2}}(g)+\frac{1}{2}{{O}_{2}}(g)\xrightarrow{{}}NO(g);\] \[\Delta {{H}^{o}}=90.3\,kJ,\Delta {{S}^{o}}=3.0\,\text{eu}\]
done
clear
C)
\[2N{{O}_{2}}(g)\xrightarrow{{}}{{N}_{2}}{{O}_{4}}(g)\] \[\Delta {{H}^{o}}=-56.0\,kJ\,\Delta {{S}^{o}}=-17.7\text{eu}\]
done
clear
D)
\[{{H}_{2}}{{O}_{2}}(g)\xrightarrow{{}}{{H}_{2}}O(l)+\frac{1}{2}{{O}_{2}}(g)\] \[\Delta {{H}^{o}}=-98.3\,kJ\Delta {{S}^{o}}=80.0\,\text{eu}\]
done
clear
View Answer play_arrow
question_answer 143) During a redox titration involving a solution containing \[\text{F}{{\text{e}}^{\text{2+}}}\]ions against\[\text{MnO}_{4}^{-}\]in the presence of excess of \[{{\text{H}}^{\text{+}}}\]ions, the number of electrons that gets transferred is.
A)
6
done
clear
B)
5
done
clear
C)
4
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 144) The oxidation state of sulphur in sodium tetrathionate \[\text{(N}{{\text{a}}_{2}}{{\text{S}}_{4}}{{\text{O}}_{6}}\text{)}\]is
A)
2
done
clear
B)
0
done
clear
C)
2.5
done
clear
D)
3.5
done
clear
View Answer play_arrow
question_answer 145) Galvanic cell is a device in which
A)
chemical energy is converted into electrical energy
done
clear
B)
electrical energy is converted into chemical energy
done
clear
C)
chemical energy is seen in the form of heat
done
clear
D)
thermal energy from an outside source is used to drive the cell reaction
done
clear
View Answer play_arrow
question_answer 146) The relationship between Gibbs' free energy change\[(\Delta G)\]and emf\[(E)\]of a reversible electrochemical cell is given by
A)
\[\Delta G=nFE\]
done
clear
B)
\[\Delta G=nF/E\]
done
clear
C)
\[\Delta G=-nFE\]
done
clear
D)
\[\Delta G=E/nF\]
done
clear
View Answer play_arrow
question_answer 147) The units of van der Waals' constants a, b respectively, are
A)
\[\text{L}\,\,\text{at}{{\text{m}}^{\text{2}}}\,\text{mo}{{\text{l}}^{-1}}\]and \[\text{mo}{{\text{l}}^{-1}}\]
done
clear
B)
\[\text{L}\,\,\text{atm}\,\text{mo}{{\text{l}}^{2}}\]and \[\text{mol L}\]
done
clear
C)
\[{{\text{L}}^{2}}\,\,\text{atm}\,\text{mo}{{\text{l}}^{-2}}\]and \[\text{mo}{{\text{l}}^{-1}}\text{ L}\]
done
clear
D)
\[{{\text{L}}^{-2}}\,\,\text{at}{{\text{m}}^{-1}}\,\text{mo}{{\text{l}}^{-1}}\]and \[\text{L}\,\text{mo}{{\text{l}}^{-2}}\]
done
clear
View Answer play_arrow
question_answer 148) Identify the pair of gases that have equal rates of diffusion
A)
CO, NO
done
clear
B)
Np.CO
done
clear
C)
\[{{N}_{2}}O,C{{O}_{2}}\]
done
clear
D)
\[~C{{O}_{2}},N{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 149) For AX ionic crystal to exist in bcc structure, the ratio of radii \[\left( \frac{{{r}_{cation}}}{{{r}_{anion}}} \right)\] should be
A)
between 0.41 and 0.73
done
clear
B)
greater than 0.73
done
clear
C)
less than 0.41
done
clear
D)
equal to 1.0
done
clear
View Answer play_arrow
question_answer 150) Identify the correct statement for the adsorption of a real gas on charcoal at 1 atm and \[\text{15}{{\,}^{\text{o}}}\text{C}\text{.}\]
A)
gases which are small in molecular size are adsorbed more
done
clear
B)
decrease in pressure increases the extent of adsorption
done
clear
C)
gases which are easily liquefiable are adsorbed more in quantity
done
clear
D)
gas which has a behaviour similar to an inert gas is adsorbed more
done
clear
View Answer play_arrow
question_answer 151) The probability that number selected at random from the number 1, 2, 3, 4, 5, 6, 7, 8, ..., 100 is a prime, is
A)
\[0.4\]
done
clear
B)
\[0.25\]
done
clear
C)
\[0.45\]
done
clear
D)
\[0.43\]
done
clear
View Answer play_arrow
question_answer 152) \[\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{m}}-1}{{{x}^{n}}-1}\]is equal to
A)
\[\frac{n}{m}\]
done
clear
B)
\[\frac{m}{n}\]
done
clear
C)
\[\frac{2m}{n}\]
done
clear
D)
\[\frac{2n}{m}\]
done
clear
View Answer play_arrow
question_answer 153) \[\underset{x\to 0}{\mathop{\lim }}\,\,\,\frac{{{e}^{5x}}-{{e}^{4x}}}{x}\]is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[4\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow
question_answer 154) If the function s\[f:R\to R\] given by \[f(x)=\left\{ \begin{matrix} x+a, & if & x\le 1 \\ 3-{{x}^{2}}, & if & x>1 \\ \end{matrix} \right.\] is continuous at \[x=1,\] then a is equal to
A)
\[4\]
done
clear
B)
\[3\]
done
clear
C)
\[2\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 155) If n[A] denotes the number of elements in the Set A and if \[n(A)=4,\,n(B)=5,\] and \[(A\cap B)=3,\]then \[n[(A\times B)\cap (B\times A)]\] is equal to
A)
\[8\]
done
clear
B)
\[9\]
done
clear
C)
\[10\]
done
clear
D)
\[11\]
done
clear
View Answer play_arrow
question_answer 156) The function \[f:R\to R\] given by \[f(x)={{x}^{3}}-1\] is
A)
a one-one function
done
clear
B)
an onto function
done
clear
C)
a bijection
done
clear
D)
neither one-one nor onto
done
clear
View Answer play_arrow
question_answer 157) If \[\omega \] is a non-real cube root of unity, then \[1+\omega +{{\omega }^{2}}+....+{{\omega }^{101}}\] is equal to
A)
\[1\]
done
clear
B)
\[\omega \]
done
clear
C)
\[{{\omega }^{2}}\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 158) The square roots of \[-7-24\sqrt{-1}\] are
A)
\[\pm (4+3\sqrt{-1})\]
done
clear
B)
\[\pm (3+4\sqrt{-1})\]
done
clear
C)
\[\pm (3-4\sqrt{-1})\]
done
clear
D)
\[\pm (4-3\sqrt{-1})\]
done
clear
View Answer play_arrow
question_answer 159) A value of k for which the quadratic equation \[{{x}^{2}}-2x(1+3k)+7(2k+3)=0\]has equal roots, is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 160) If \[\alpha ,\beta \] are the roots of the equation \[{{x}^{2}}+ax+b=0,\] then \[\frac{1}{{{\alpha }^{2}}}+\frac{1}{{{\beta }^{2}}}\]is equal to
A)
\[\frac{{{a}^{2}}-2b}{{{b}^{2}}}\]
done
clear
B)
\[\frac{{{b}^{2}}-2a}{{{b}^{2}}}\]
done
clear
C)
\[\frac{{{a}^{2}}+2b}{{{b}^{2}}}\]
done
clear
D)
\[\frac{{{b}^{2}}+2a}{{{b}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 161) If \[|a|<1,\] then \[1+2a+3{{a}^{2}}+4{{a}^{3}}+.....\] is equal to
A)
\[\frac{1}{1-a}\]
done
clear
B)
\[\frac{1}{1+a}\]
done
clear
C)
\[\frac{1}{1+{{a}^{2}}}\]
done
clear
D)
\[\frac{1}{{{(1-a)}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 162) If pth term of an arithmetic progression is q and the qth term is p, then 10th term is
A)
\[p-q+10\]
done
clear
B)
\[p+q+11\]
done
clear
C)
\[p+q-9\]
done
clear
D)
\[p+q-10\]
done
clear
View Answer play_arrow
question_answer 163) If \[{{C}_{0}},{{C}_{1}},{{C}_{2}},.....{{C}_{n}}\] denotes the binomial coefficients in the expansion of \[{{(1+x)}^{n}},\]then \[{{C}_{0}}+\frac{{{C}_{1}}}{2}+\frac{{{C}_{2}}}{3}+....+\frac{{{C}_{n}}}{n+1}\] is equal to
A)
\[\frac{{{2}^{n+1}}-1}{n+1}\]
done
clear
B)
\[\frac{{{2}^{n}}-1}{n}\]
done
clear
C)
\[\frac{{{2}^{n-1}}-1}{n-1}\]
done
clear
D)
\[\frac{{{2}^{n+1}}-1}{n+2}\]
done
clear
View Answer play_arrow
question_answer 164) The coefficient of \[{{x}^{r}}\] in the expansion of \[{{(1-x)}^{-2}}\]is
A)
\[r\]
done
clear
B)
\[r+1\]
done
clear
C)
\[r+3\]
done
clear
D)
\[r-1\]
done
clear
View Answer play_arrow
question_answer 165) The number of permutations of 4 letters that can be made out of the letters of the word EXAMINATION is
A)
\[2454\]
done
clear
B)
\[2452\]
done
clear
C)
\[2450\]
done
clear
D)
\[1806\]
done
clear
View Answer play_arrow
question_answer 166) \[\frac{1}{3!}+\frac{2}{5!}+\frac{3}{7!}+...\] is equal to
A)
\[\frac{{{e}^{-1}}}{2}\]
done
clear
B)
\[e\]
done
clear
C)
\[\frac{e}{4}\]
done
clear
D)
\[\frac{e}{6}\]
done
clear
View Answer play_arrow
question_answer 167) \[\frac{x-y}{x}+\frac{1}{2}{{\left( \frac{x-y}{x} \right)}^{2}}+\frac{1}{3}{{\left( \frac{x-y}{x} \right)}^{3}}+....\] is equal to
A)
\[{{\log }_{e}}\,(x-y)\]
done
clear
B)
\[{{\log }_{e}}\,(x+y)\]
done
clear
C)
\[{{\log }_{e}}\,\left( \frac{x}{y} \right)\]
done
clear
D)
\[{{\log }_{e}}\,\,xy\]
done
clear
View Answer play_arrow
question_answer 168) The standard deviation of the first n natural numbers is
A)
\[\frac{\sqrt{{{n}^{2}}+1}}{12}\]
done
clear
B)
\[\frac{{{n}^{2}}-1}{12}\]
done
clear
C)
\[\sqrt{\frac{{{n}^{2}}-1}{12}}\]
done
clear
D)
\[\frac{{{n}^{2}}+1}{12}\]
done
clear
View Answer play_arrow
question_answer 169) A point P moves so that the sum of its distances from \[(-ae,\,0)\]and \[(ae,\,0)\] is\[2a\]. Then the locus of P is
A)
\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{x}^{2}}}{{{a}^{2}}(1-{{e}^{2}})}=1\]
done
clear
B)
\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}(1-{{e}^{2}})}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}(1+{{e}^{2}})}=1\]
done
clear
D)
\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{a}^{2}}(1+{{e}^{2}})}=1\]
done
clear
View Answer play_arrow
question_answer 170) The length of the perpendicular from the origin to the line \[\frac{x\,\,\sin \alpha }{b}-\frac{y\,\cos \,\alpha }{a}-1=0\] is
A)
\[\frac{|ab|}{\sqrt{{{a}^{2}}\,{{\cos }^{2}}\alpha -{{b}^{2}}\,{{\sin }^{2}}\alpha }}\]
done
clear
B)
\[\frac{|ab|}{\sqrt{{{a}^{2}}\,{{\cos }^{2}}\alpha +{{b}^{2}}\,{{\sin }^{2}}\alpha }}\]
done
clear
C)
\[\frac{|ab|}{\sqrt{{{a}^{2}}\,si{{n}^{2}}\alpha -{{b}^{2}}\,{{\cos }^{2}}\alpha }}\]
done
clear
D)
\[\frac{|ab|}{\sqrt{{{a}^{2}}\,si{{n}^{2}}\alpha +{{b}^{2}}\,{{\cos }^{2}}\alpha }}\]
done
clear
View Answer play_arrow
question_answer 171) The distance between the parallel lines \[y=x+a,\,\,y=x+b\]is
A)
\[\frac{|b-a|}{\sqrt{2}}\]
done
clear
B)
\[|a-b|\]
done
clear
C)
\[|a+b|\]
done
clear
D)
\[\frac{|a+b|}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 172) The line passing through the point of intersection of \[x+y=2,\,x-y=0\] and is parallel to \[x+2y=5\]is
A)
\[x+2y=1\]
done
clear
B)
\[x+2y=2\]
done
clear
C)
\[x+2y=4\]
done
clear
D)
\[x+2y=3\]
done
clear
View Answer play_arrow
question_answer 173) If the line \[y=7x-25\]meets the circle \[{{x}^{2}}+{{y}^{2}}=25\]in the points A, B then the distance between A and B is
A)
\[\sqrt{10}\]
done
clear
B)
\[10\]
done
clear
C)
\[5\sqrt{2}\]
done
clear
D)
\[5\]
done
clear
View Answer play_arrow
question_answer 174) One of the directrices of the ellipse \[8{{x}^{2}}+6{{y}^{2}}-16x+12y+13=0\]is
A)
\[3y-3=\sqrt{6}\]
done
clear
B)
\[3y+3=\sqrt{6}\]
done
clear
C)
\[y+1=\sqrt{3}\]
done
clear
D)
\[y-1=-\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 175) If OAB is an equilateral triangle inscribed in the parabola \[{{y}^{2}}=4ax\] with O as the vertex, then the length of the side of the\[\Delta \,\,OAB\] is
A)
\[8\,a\,\sqrt{3}\]
done
clear
B)
\[4\,a\,\sqrt{3}\]
done
clear
C)
\[2\,a\,\sqrt{3}\]
done
clear
D)
\[a\,\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 176) If \[x\,\sin \theta =y\,\cos \theta =\frac{2z\,\tan \theta }{1-{{\tan }^{2}}\theta },\] then \[4{{z}^{2}}({{x}^{2}}+{{y}^{2}})\] is equal to
A)
\[{{({{x}^{2}}+{{y}^{2}})}^{3}}\]
done
clear
B)
\[{{({{x}^{2}}-{{y}^{2}})}^{3}}\]
done
clear
C)
\[{{({{x}^{2}}-{{y}^{2}})}^{2}}\]
done
clear
D)
\[{{({{x}^{2}}+{{y}^{2}})}^{2}}\]
done
clear
View Answer play_arrow
question_answer 177) \[\tan {{25}^{o}}+\tan {{20}^{o}}+\tan {{25}^{o}}\,\tan {{20}^{o}}\] is equal to
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 178) If \[\cos x=3\cos y,\] then \[2\tan \frac{y-x}{2}\] is equal to
A)
\[\cot \left( \frac{y-x}{2} \right)\]
done
clear
B)
\[\cot \left( \frac{x+y}{4} \right)\]
done
clear
C)
\[\cot \left( \frac{y-x}{4} \right)\]
done
clear
D)
\[\cot \left( \frac{y-x}{4} \right)\]
done
clear
View Answer play_arrow
question_answer 179) In any \[\Delta \,ABC\] under usual notation, \[a(b\,\cos \,C-c\,\cos B)\] is equal to
A)
\[{{b}^{2}}-{{c}^{2}}\]
done
clear
B)
\[{{c}^{2}}-{{b}^{2}}\]
done
clear
C)
\[\frac{{{b}^{2}}-{{c}^{2}}}{2}\]
done
clear
D)
\[\frac{{{c}^{2}}-{{b}^{2}}}{2}\]
done
clear
View Answer play_arrow
question_answer 180) If \[4\,\sin \,A=4\,\sin B=3\,\sin \,C\] in a triangle ABC, then \[\cos \,\,C\] is equal to
A)
\[1/3\]
done
clear
B)
\[1/9\]
done
clear
C)
\[1/27\]
done
clear
D)
\[~1/18\]
done
clear
View Answer play_arrow
question_answer 181) If \[\cos \,x\ne \frac{1}{2},\] then the solutions of \[\cos \,x+\cos \,2x+\cos \,3x=0\]are
A)
\[2n\pi \pm \frac{\pi }{4},n\in Z\]
done
clear
B)
\[2n\pi \pm \frac{\pi }{3},n\in Z\]
done
clear
C)
\[2n\pi \pm \frac{\pi }{6},n\in Z\]
done
clear
D)
\[2n\pi \pm \frac{\pi }{2},n\in Z\]
done
clear
View Answer play_arrow
question_answer 182) \[{{\tan }^{-1}}\,\frac{x}{\sqrt{{{a}^{2}}-{{x}^{2}}}}\]is equal to
A)
\[2{{\sin }^{-1}}\frac{x}{a}\]
done
clear
B)
\[{{\sin }^{-1}}\frac{2x}{a}\]
done
clear
C)
\[{{\sin }^{-1}}\frac{x}{a}\]
done
clear
D)
\[{{\cos }^{-1}}\frac{x}{a}\]
done
clear
View Answer play_arrow
question_answer 183) The solution of \[{{\tan }^{-1}}\,2\theta +{{\tan }^{-1}}3\theta =\frac{\pi }{4}\] is
A)
\[\frac{1}{\sqrt{3}}\]
done
clear
B)
\[\frac{1}{3}\]
done
clear
C)
\[\frac{1}{6}\]
done
clear
D)
\[\frac{1}{\sqrt{6}}\]
done
clear
View Answer play_arrow
question_answer 184) The number of solutions of \[\sin x=\sin 2x\]between \[\frac{-\pi }{2}\] and \[\frac{\pi }{2}\] is
A)
\[3\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 185) If \[y=\frac{3a{{t}^{2}}}{1+{{t}^{3}}},\,x=\frac{3at}{1+{{t}^{3}}},\] then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{t(2-{{t}^{3}})}{(1-2{{t}^{3}})}\]
done
clear
B)
\[\frac{t(2+{{t}^{3}})}{(1-2{{t}^{3}})}\]
done
clear
C)
\[\frac{t(2-{{t}^{3}})}{(1+2{{t}^{3}})}\]
done
clear
D)
\[\frac{t(2+{{t}^{3}})}{(1+2{{t}^{3}})}\]
done
clear
View Answer play_arrow
question_answer 186) If \[y={{\sec }^{-1}}\left( \frac{1}{\sqrt{1-{{x}^{2}}}} \right),\] then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{1}{\sqrt{1-{{x}^{2}}}}\]
done
clear
B)
\[\frac{2}{\sqrt{1-{{x}^{2}}}}\]
done
clear
C)
\[\frac{1}{\sqrt{1+{{x}^{2}}}}\]
done
clear
D)
\[\frac{2}{\sqrt{1+{{x}^{2}}}}\]
done
clear
View Answer play_arrow
question_answer 187) The point on the curve \[y={{x}^{3}}\]at which the tangent to the curve is parallel to the x axis, is
A)
\[(2,2)\]
done
clear
B)
\[(3,3)\]
done
clear
C)
\[(4,4)\]
done
clear
D)
\[(0,0)\]
done
clear
View Answer play_arrow
question_answer 188) The equation of normal to the curve \[{{x}^{2}}y={{x}^{2}}-3x+6\] at the point with abscissa \[x=3\]is
A)
\[3x+27y=79\]
done
clear
B)
\[27\text{ }x-3y=79\]
done
clear
C)
\[27x+3y=79\]
done
clear
D)
\[3x-27y=79\]
done
clear
View Answer play_arrow
question_answer 189) The function \[f(x)=2{{x}^{3}}+3{{x}^{2}}-12x+1\] decreases in the interval
A)
\[(2,3)\]
done
clear
B)
\[(1,2)\]
done
clear
C)
\[(-2,1)\]
done
clear
D)
\[(-3,-2)\]
done
clear
View Answer play_arrow
question_answer 190) The function \[f(x)={{x}^{2}}{{e}^{-x}}\] increases in the interval
A)
\[(0,2)\]
done
clear
B)
\[(2,3)\]
done
clear
C)
\[(3,4)\]
done
clear
D)
\[(4,5)\]
done
clear
View Answer play_arrow
question_answer 191) The number of real roots of \[f(x)=0,\]where \[f(x)=(x-1)(x-2)(x-3)(x-4)\] lying the interval \[(1,3)\] is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 192) If \[{{x}^{y}}={{y}^{x}},\] then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{{{y}^{2}}-xy\,\log \,y}{{{x}^{2}}-xy\,\log \,x}\]
done
clear
B)
\[\frac{{{y}^{2}}+xy\,\log \,y}{{{x}^{2}}+xy\,\log \,x}\]
done
clear
C)
\[\frac{{{y}^{2}}-xy\,\log \,x}{{{x}^{2}}-xy\,\log \,y}\]
done
clear
D)
\[\frac{{{y}^{2}}+xy\,\log \,y}{{{x}^{2}}-xy\,\log \,x}\]
done
clear
View Answer play_arrow
question_answer 193) Rectilinear motion is performed in accordance with the formulae \[s=\frac{2}{9}\sin \frac{\pi t}{2}+{{s}_{0}}.\] Then the acceleration at the end of the 1st second (in\[cm/{{s}^{2}}\]) is
A)
\[\frac{{{\pi }^{2}}}{18}\]
done
clear
B)
\[\frac{{{\pi }^{2}}}{7}\]
done
clear
C)
\[\frac{-{{\pi }^{2}}}{9}\]
done
clear
D)
\[\frac{-{{\pi }^{2}}}{18}\]
done
clear
View Answer play_arrow
question_answer 194) A value on x in the interval \[(1,2)\] such that \[f'(x)=0,\] where \[f(x)={{x}^{3}}-3{{x}^{2}}+2x+10\] is
A)
\[\frac{3+\sqrt{3}}{3}\]
done
clear
B)
\[\frac{3+\sqrt{2}}{2}\]
done
clear
C)
\[1+\sqrt{2}\]
done
clear
D)
\[\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 195) Given that the force acting on a material point is inversely proportional to the velocity of the moving point. Then the kinetic energy of the point is a ...... function of time.
A)
exponential
done
clear
B)
linear
done
clear
C)
second degree
done
clear
D)
non-linear
done
clear
View Answer play_arrow
question_answer 196) If \[f(x)={{x}^{2}}-5x,A=\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \\ \end{matrix} \right],\] then \[f(A)\] is equal to
A)
\[\left[ \begin{matrix} -7 & 0 \\ 0 & -7 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 0 & -7 \\ -7 & 0 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 7 & 0 \\ 0 & 7 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 0 & 7 \\ 7 & 0 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 197) If A is a square matrix. A' its transpose, then \[\frac{1}{2}(A-A')\]is
A)
a symmetric matrix
done
clear
B)
a skew symmetric matrix
done
clear
C)
a unit matrix
done
clear
D)
an elementary matrix
done
clear
View Answer play_arrow
question_answer 198) The number of solutions of the system of equations \[x-y+z=2\] \[2x+y-z=5\] \[4x+y+z=10\] is
A)
\[\infty \]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 199) The adjoin of the matrix\[\left[ \begin{matrix} \cos \,\theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right]\]is
A)
\[\left[ \begin{matrix} \cos \,\theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} sin\,\theta & \cos \theta \\ \cos \theta & sin\theta \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} \cos \,\theta & sin\theta \\ -sin\theta & \cos \theta \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} -sin\,\theta & \cos \theta \\ \cos \theta & sin\theta \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 200) If \[x\ne 0,\,\left| \begin{matrix} x+1 & 2x+1 & 3x+1 \\ 2x & 4x+3 & 6x+3 \\ 4x+4 & 6x+4 & 8x+4 \\ \end{matrix} \right|=0,\] then \[x+1\] is equal to
A)
\[x\]
done
clear
B)
\[0\]
done
clear
C)
\[2x\]
done
clear
D)
\[3x\]
done
clear
View Answer play_arrow
question_answer 201) \[\left| \begin{matrix} 1 & x & y+z \\ 1 & y & z+x \\ 1 & z & x+y \\ \end{matrix} \right|\] is equal to
A)
\[0\]
done
clear
B)
\[x\]
done
clear
C)
\[y\]
done
clear
D)
\[xyz\]
done
clear
View Answer play_arrow
question_answer 202) If P is any point with in a triangle ABC, then \[\overrightarrow{PA}+\overrightarrow{CP}\] is equal to
A)
\[\overrightarrow{AC}+\overrightarrow{CB}\]
done
clear
B)
\[\overrightarrow{BC}+\overrightarrow{BA}\]
done
clear
C)
\[\overrightarrow{CB}+\overrightarrow{AB}\]
done
clear
D)
\[\overrightarrow{CB}+\overrightarrow{BA}\]
done
clear
View Answer play_arrow
question_answer 203) If the vector \[3i-2\hat{j}-5\hat{k}\] is perpendicular to \[c\hat{k}-\hat{j}+6\hat{i},\] then c is equal to
A)
\[3\]
done
clear
B)
\[4\]
done
clear
C)
\[5\]
done
clear
D)
\[6\]
done
clear
View Answer play_arrow
question_answer 204) The vector \[\vec{a}\times (\vec{b}\times \vec{c})\] is coplanar with the vectors
A)
\[\vec{b},\,\vec{c}\]
done
clear
B)
\[\vec{a},\,\vec{b}\]
done
clear
C)
\[\vec{a},\,\vec{c}\]
done
clear
D)
\[\vec{a},\,\,\vec{b}\,,\vec{c}\]
done
clear
View Answer play_arrow
question_answer 205) If \[\vec{a},\,\,\vec{b}\,\] are any two vectors, then \[(2\vec{a}+3\vec{b})\times (5\vec{a}+7\vec{b})+\vec{a}\times \vec{b}\] is equal to
A)
\[\vec{0}\]
done
clear
B)
\[0\]
done
clear
C)
\[\vec{a}\times \vec{b}\]
done
clear
D)
\[\vec{b}\times \vec{a}\]
done
clear
View Answer play_arrow
question_answer 206) A unit vector perpendicular to \[\hat{i}-\hat{j}+\hat{k}\]and \[\hat{i}+\hat{j}-\hat{k}\] is
A)
\[\frac{\hat{k}+\hat{i}}{\sqrt{2}}\]
done
clear
B)
\[\frac{\hat{j}+\hat{k}}{\sqrt{2}}\]
done
clear
C)
\[\frac{\hat{i}-\hat{k}}{\sqrt{3}}\]
done
clear
D)
\[\frac{\hat{j}-\hat{k}}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 207) If \[\vec{a}\times \vec{b}=\vec{c}\times \vec{d}\]and \[\vec{a}\times \vec{c}=\vec{b}\times \vec{d},\] then \[\vec{a}-\vec{d}\] is parallel to
A)
\[\vec{b}+\vec{c}\]
done
clear
B)
\[\vec{b}-2\vec{c}\]
done
clear
C)
\[\vec{b}+2\vec{c}\]
done
clear
D)
\[\vec{b}-\vec{c}\]
done
clear
View Answer play_arrow
question_answer 208) \[3a{{\int_{0}^{1}{\left( \frac{ax-1}{a-1} \right)}}^{2}}\,\,dx\]is equal to
A)
\[a-1+{{(a-1)}^{-2}}\]
done
clear
B)
\[a+{{a}^{-2}}\]
done
clear
C)
\[a-{{a}^{-2}}\]
done
clear
D)
\[{{a}^{2}}+\frac{1}{{{a}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 209) \[\int_{-\pi /2}^{\pi /2}{\frac{dx}{1+\cos x}}\] is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 210) \[\int{\sin \,\,\sqrt{x}}\,\,dx\] is equal to
A)
\[\sin \sqrt{x}-\sqrt{x}\,\cos \,\sqrt{x}\]
done
clear
B)
\[2(\sin \,\sqrt{x}-\sqrt{x}\,\cos \,\sqrt{x})+c\]
done
clear
C)
\[\cos \,\sqrt{x}-\sqrt{x}\,\sin \,\sqrt{x}+c\]
done
clear
D)
\[2(\cos \sqrt{x}-\sqrt{x}\,\sin \sqrt{x})+c\]
done
clear
View Answer play_arrow
question_answer 211) \[\int{\frac{\sqrt{x}}{x+1}\,dx}\] is equal to
A)
\[2(\sqrt{x}+{{\tan }^{-1}}\sqrt{x})+c\]
done
clear
B)
\[2(\sqrt{x}+{{\cot }^{-1}}\sqrt{x})+c\]
done
clear
C)
\[2(\sqrt{x}-{{\cot }^{-1}}-\sqrt{x})+c\]
done
clear
D)
\[2(\sqrt{x}-ta{{n}^{-1}}\sqrt{x})+c\]
done
clear
View Answer play_arrow
question_answer 212) The area (in square unit) bounded by the curves \[y={{x}^{3}}\]and \[y=x\] is
A)
\[1/2\text{ }sq\text{ }unit\]
done
clear
B)
\[1/4\text{ }sq\text{ }unit\]
done
clear
C)
\[1/8\text{ }sq\text{ }unit\]
done
clear
D)
\[1/16\text{ }sq\text{ }unit\]
done
clear
View Answer play_arrow
question_answer 213) The area (in square unit) bounded by the curves \[4y={{x}^{2}}\]and \[2y=6-{{x}^{2}}\]is
A)
\[8\]
done
clear
B)
\[6\]
done
clear
C)
\[4\]
done
clear
D)
\[10\]
done
clear
View Answer play_arrow
question_answer 214) The general solution of the differential equation \[\frac{dy}{dx}=\frac{(1+{{y}^{2}})}{xy(1+{{x}^{2}})}\] is
A)
\[(1+{{x}^{2}})(1+{{y}^{2}})=c\]
done
clear
B)
\[(1+{{x}^{2}})(1+{{y}^{2}})=c{{x}^{2}}\]
done
clear
C)
\[(1-{{x}^{2}})(1-{{y}^{2}})=c\]
done
clear
D)
\[(1+{{x}^{2}})(1+{{y}^{2}})=c{{y}^{2}}\]
done
clear
View Answer play_arrow
question_answer 215) A particle moves along a straight line with the law of motion given by \[{{s}^{2}}=a{{t}^{2}}+2bt+c\]. Then the acceleration varies are
A)
\[1/{{s}^{3}}\]
done
clear
B)
\[1/s\]
done
clear
C)
\[~1/{{s}^{4}}\]
done
clear
D)
\[1/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 216) A point is moving with uniform acceleration in the eleventh and fifteenth seconds from the commencement it moves through 720 and 960 cm respectively. Its initial velocity and the acceleration with which it moves are
A)
\[60\text{ }m/s,\text{ }40\text{ }m/{{s}^{2}}\]
done
clear
B)
\[70\text{ }m/s,\text{ }30\text{ }m/{{s}^{2}}\]
done
clear
C)
\[90\text{ }m/s,\text{ }60\text{ }m/{{s}^{2}}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 217) A particle of mass m is projected from a fixed point 0 into the air with velocity u in a direction making an angle a with the horizontal. Then the motion of the particle describes a parabola with the latusrectum is
A)
\[\frac{2}{g}{{(horizontal\text{ }velocity)}^{2}}\]
done
clear
B)
\[\frac{2}{g}(vertical\text{ }velocity)\]
done
clear
C)
\[\frac{2}{{{g}^{2}}}{{(horizontal\text{ }velocity)}^{2}}\]
done
clear
D)
\[\frac{2}{{{g}^{2}}}{{(vertical\text{ }velocity)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 218) The vector equation of the line passing through the points \[(3,2,1)\] and \[(-2,1,3)\] is
A)
\[\vec{r}=3\hat{i}+2\hat{j}+\hat{k}+\lambda (-5\hat{i}-\hat{j}+2\hat{k})\]
done
clear
B)
\[\vec{r}=3\hat{i}+2\hat{j}+\hat{k}+\lambda (-5\hat{i}+\hat{j}+\hat{k})\]
done
clear
C)
\[\vec{r}=-2\hat{i}+\hat{j}+3\hat{k}+\lambda (5\hat{i}+\hat{j}+2\hat{k})\]
done
clear
D)
\[\vec{r}=-2\hat{i}+\hat{j}+\hat{k}+\lambda (5\hat{i}+\hat{j}+2\hat{k})\]
done
clear
View Answer play_arrow
question_answer 219) The line \[\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\] meets the plane \[2x+3y-z=-4\]in the point
A)
\[(1,2,3)\]
done
clear
B)
\[(-1,-1,-1)\]
done
clear
C)
\[(2,1,3)\]
done
clear
D)
\[(1,1,1)\]
done
clear
View Answer play_arrow
question_answer 220) The shortest distance between the lines \[1+x=2y=-12z\]and \[x=y+2=6z-6\]is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 221) The foot of the perpendicular from \[(2,4,-1)\]to the line \[x+5=\frac{1}{4}(y+3)=-\frac{1}{9}(z-6)\]
A)
\[(-4,1,-3)\]
done
clear
B)
\[(4,-1,-3)\]
done
clear
C)
\[(-4,-1,3)\]
done
clear
D)
\[(-4,-1,-3)\]
done
clear
View Answer play_arrow
question_answer 222) The radius of the sphere \[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=x+2y+3z\]is
A)
\[\frac{\sqrt{14}}{2}\]
done
clear
B)
\[\sqrt{7}\]
done
clear
C)
\[\frac{7}{2}\]
done
clear
D)
\[\frac{\sqrt{7}}{2}\]
done
clear
View Answer play_arrow
question_answer 223) The distance between the planes \[2x-2y+z+3=0\]and \[4x-4y+2z+5=0\] is
A)
\[3\]
done
clear
B)
\[6\]
done
clear
C)
\[\frac{1}{6}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
View Answer play_arrow
question_answer 224) If B is a Boolean algebra and \[a,\,\,b\,\,\in \,B,\] then \[a.(a+b)\]is equal to
A)
\[a\]
done
clear
B)
\[b\]
done
clear
C)
\[1\]
done
clear
D)
\[a'\]
done
clear
View Answer play_arrow
question_answer 225) Let \[{{E}_{1}},{{E}_{2}}\] be two mutually exclusive events of an experiment with \[P(not\,{{E}_{2}})=0.6=P({{E}_{1}}\cup {{E}_{2}}).\]Then \[P({{E}_{1}})\] is equal to
A)
\[0.1\]
done
clear
B)
\[0.3\]
done
clear
C)
\[0.4\]
done
clear
D)
\[0.2\]
done
clear
View Answer play_arrow
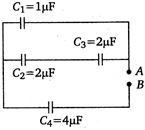
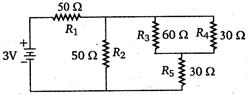
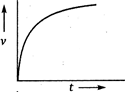
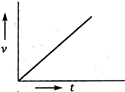
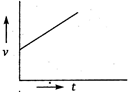
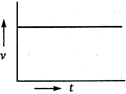
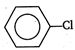
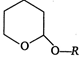 is
is