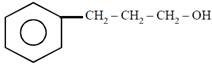-
question_answer1) From the following combinations of physical constants (expressed through their usual symbols) the only combination, that would have the same value in different systems of units, is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{ch}{2\pi \varepsilon _{o}^{2}}\]
done
clear
B)
\[\frac{{{e}^{2}}}{2\pi \varepsilon _{o}^{{}}Gm_{e}^{2}}\](\[{{m}_{e}}=\] mass of electron)
done
clear
C)
\[\frac{{{\mu }_{o}}{{\varepsilon }_{o}}}{{{c}^{2}}}\frac{G}{h{{e}^{2}}}\]
done
clear
D)
\[\frac{2\pi \sqrt{{{\mu }_{o}}{{\varepsilon }_{o}}}}{c{{e}^{2}}}\frac{h}{G}\]
done
clear
View Answer play_arrow
-
question_answer2) A person climbs up a stalled escalator in 60 s. If standing on the same but escalator running with constant velocity he takes 40 s. How much time is taken by the person to walk up the moving escalator?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
37 s
done
clear
B)
27 s
done
clear
C)
24 s
done
clear
D)
45 s
done
clear
View Answer play_arrow
-
question_answer3)
Three masses m, 2m and 3m are moving in x-y plane with speed 3u, 2u and u respectively as shown in figure. The three masses collide at the same point at P and stick together. The velocity of resulting mass will be: 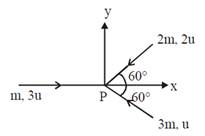 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{u}{12}\left( \hat{i}+\sqrt{3}\hat{j} \right)\]
done
clear
B)
\[\frac{u}{12}\left( \hat{i}-\sqrt{3}\hat{j} \right)\]
done
clear
C)
\[\frac{u}{12}\left( -\hat{i}+\sqrt{3}\hat{j} \right)\]
done
clear
D)
\[\frac{u}{12}\left( -\hat{i}-\sqrt{3}\hat{j} \right)\]
done
clear
View Answer play_arrow
-
question_answer4) A bullet of mass 4g is fired horizontally with a speed of 300 m/s into 0.8 kg block of wood at rest on a table. If the coefficient of friction between the block and the table is 0.3, how far will the block slide approximately?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
0.19 m
done
clear
B)
0.379 m
done
clear
C)
0.569 m
done
clear
D)
0.758 m
done
clear
View Answer play_arrow
-
question_answer5) A spring of unstretched length l has a mass m with one end fixed to a rigid support. Assuming spring to be made of a uniform wire, the kinetic energy possessed by it if its free end is pulled with uniform velocity v is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{1}{2}m{{v}^{2}}\]
done
clear
B)
\[m{{v}^{2}}\]
done
clear
C)
\[\frac{1}{3}m{{v}^{2}}\]
done
clear
D)
\[\frac{1}{6}m{{v}^{2}}\]
done
clear
View Answer play_arrow
-
question_answer6)
A particle is moving in a circular path of radius a, with a constant velocity v as shown in the figure. The centre of circle is marked by 'C'. The angular momentum from the origin O can be written as: 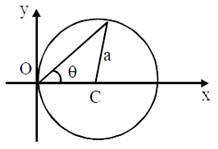 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[va(1+cos2\theta )\]
done
clear
B)
\[va(1+cos\theta )\]
done
clear
C)
\[vacos2\theta \]
done
clear
D)
\[va\]
done
clear
View Answer play_arrow
-
question_answer7)
 Two hypothetical planets of masses m1 and m2 are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ?d?? (Speed of \[{{m}_{1}}\] is \[{{v}_{1}}\] and that of \[{{m}_{2}}\] is \[{{v}_{2}}\])
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
Two hypothetical planets of masses m1 and m2 are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ?d?? (Speed of \[{{m}_{1}}\] is \[{{v}_{1}}\] and that of \[{{m}_{2}}\] is \[{{v}_{2}}\])
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{v}_{1}}={{v}_{2}}\]
done
clear
B)
\[{{v}_{1}}={{m}_{2}}\sqrt{\frac{2G}{d\left( {{m}_{1}}+{{m}_{2}} \right)}}\] \[{{v}_{2}}={{m}_{1}}\sqrt{\frac{2G}{d\left( {{m}_{1}}+{{m}_{2}} \right)}}\]
done
clear
C)
\[{{v}_{1}}={{m}_{1}}\sqrt{\frac{2G}{d\left( {{m}_{1}}+{{m}_{2}} \right)}}\]\[{{v}_{2}}={{m}_{2}}\sqrt{\frac{2G}{d\left( {{m}_{1}}+{{m}_{2}} \right)}}\]
done
clear
D)
\[{{v}_{2}}={{m}_{2}}\sqrt{\frac{2G}{{{m}_{1}}}}\] \[{{v}_{2}}={{m}_{2}}\sqrt{\frac{2G}{{{m}_{2}}}}\]
done
clear
View Answer play_arrow
-
question_answer8) Steel ruptures when a shear of \[3.5\times {{10}^{8}}N{{m}^{-2}}\]is applied. The force needed to punch a 1 cm diameter hole in a steel sheet 0.3 cm thick is nearly:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[1.4\times {{10}^{4}}N\]
done
clear
B)
\[2.7\times {{10}^{4}}N\]
done
clear
C)
\[3.3\times {{10}^{4}}N\]
done
clear
D)
\[1.1\times {{10}^{4}}N\]
done
clear
View Answer play_arrow
-
question_answer9) A cylindrical vessel of cross-section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{2A}{\pi {{a}^{2}}}\sqrt{\frac{h}{g}}\]
done
clear
B)
\[\frac{\sqrt{2}A}{\pi {{a}^{2}}}\sqrt{\frac{h}{g}}\]
done
clear
C)
\[\frac{2\sqrt{2}A}{\pi {{a}^{2}}}\sqrt{\frac{h}{g}}\]
done
clear
D)
\[\frac{A}{\sqrt{2}\pi {{a}^{2}}}\sqrt{\frac{h}{g}}\]
done
clear
View Answer play_arrow
-
question_answer10) Two soap bubbles coalesce to form a single bubble. If V is the subsequent change in volume of contained air and S change in total surface area, T is the surface tension and P atmospheric pressure, then which of the following relation is correct?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
4PV + 3ST = 0
done
clear
B)
3PV + 4ST = 0
done
clear
C)
2PV + 3ST = 0
done
clear
D)
3PV + 2ST = 0
done
clear
View Answer play_arrow
-
question_answer11) Hot water cools from \[60{}^\circ C\] to \[50{}^\circ C\] in the first 10 minutes and to \[42{}^\circ C\] in the next 10 minutes. The temperature of the surroundings is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[25{}^\circ C\]
done
clear
B)
\[10{}^\circ C\]
done
clear
C)
\[15{}^\circ C\]
done
clear
D)
\[20{}^\circ C\]
done
clear
View Answer play_arrow
-
question_answer12) A Carnot engine absorbs 1000 J of heat energy from a reservoir at \[127{}^\circ C\] and rejects 600 J of heat energy during each cycle. The efficiency of engine and temperature of sink will be:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[20%\text{ }and\,\,-43{}^\circ C\]
done
clear
B)
\[40%\text{ }and\,\,-33{}^\circ C\]
done
clear
C)
\[50%\text{ }and\,\,-20{}^\circ C\]
done
clear
D)
\[70%\text{ }and\,\,-10{}^\circ C\]
done
clear
View Answer play_arrow
-
question_answer13) At room temperature a diatomic gas is found to have an r.m.s. speed of 1930 \[\text{m}{{\text{s}}^{\text{-1}}}\]. The gas is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{H}_{2}}\]
done
clear
B)
\[C{{l}_{2}}\]
done
clear
C)
\[{{O}_{2}}\]
done
clear
D)
\[{{F}_{2}}\]
done
clear
View Answer play_arrow
-
question_answer14) Which of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a, b, c are positive constants?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[a+bx-c{{x}^{2}}\]
done
clear
B)
\[b{{x}^{2}}\]
done
clear
C)
\[a-bx+c{{x}^{2}}\]
done
clear
D)
\[-bx\]
done
clear
View Answer play_arrow
-
question_answer15) A source of sound A emitting waves of frequency 1800 Hz is falling towards ground with a terminal speed v. The observer B on the ground directly beneath the source receives waves of frequency 2150 Hz. The source A receives waves, reflected from ground of frequency nearly: (Speed of sound = 343 m/s)
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
2150 Hz
done
clear
B)
2500 Hz
done
clear
C)
1800 Hz
done
clear
D)
2400 Hz
done
clear
View Answer play_arrow
-
question_answer16) A spherically symmetric charge distribution is characterized by a charge density having the following variations: \[\rho (r)={{\rho }_{o}}\left( 1-\frac{r}{R} \right)\]for r < R\[\rho (r)=0\]for \[r\ge R\] Where r is the distance from the centre of the charge distribution \[{{\rho }_{o}}\]is a constant. The electric field at an internal point (r < R) is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{{{\rho }_{o}}}{4{{\varepsilon }_{0}}}\left( \frac{r}{3}-\frac{{{r}^{2}}}{4R} \right)\]
done
clear
B)
\[\frac{{{\rho }_{o}}}{{{\varepsilon }_{o}}}\left( \frac{r}{3}-\frac{{{r}^{2}}}{4R} \right)\]
done
clear
C)
\[\frac{{{\rho }_{o}}}{3{{\varepsilon }_{o}}}\left( \frac{r}{3}-\frac{{{r}^{2}}}{4R} \right)\]
done
clear
D)
\[\frac{{{\rho }_{o}}}{12{{\varepsilon }_{o}}}\left( \frac{r}{3}-\frac{{{r}^{2}}}{4R} \right)\]
done
clear
View Answer play_arrow
-
question_answer17) The space between the plates of a parallel plate capacitor is filled with a 'dielectric' whose 'dielectric constant' varies with distance as per the relation: \[K(x)={{K}_{o}}+\lambda x\] (\[\lambda =\] a constant) The capacitance C, of the capacitor, would be related to its vacuum capacitance Co for the relation :
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[C=\frac{\lambda d}{\ln (1+{{K}_{o}}\lambda d)}{{C}_{o}}\]
done
clear
B)
\[C=\frac{\lambda }{d.ln(1+{{K}_{o}}\lambda d)}{{C}_{o}}\]
done
clear
C)
\[C=\frac{\lambda d}{ln(1+\lambda d/{{K}_{o}})}{{C}_{o}}\]
done
clear
D)
\[C=\frac{\lambda }{d.ln(1+{{K}_{o}}/\lambda d)}{{C}_{o}}\]
done
clear
View Answer play_arrow
-
question_answer18)
The circuit shown here has two batteries of 8.0 V and 16.0 V and three resistors \[3\Omega ,9\Omega \]and \[9\Omega \] and a capacitor of 5.0 \[\mu F.\] 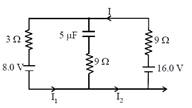 How much is the current I in the circuit in steady state?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
How much is the current I in the circuit in steady state?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1.6 A
done
clear
B)
0.67 A
done
clear
C)
2.5 A
done
clear
D)
0.25 A
done
clear
View Answer play_arrow
-
question_answer19) A positive charge 'q' of mass 'm' is moving along the + x axis. We wish to apply a uniform magnetic field B for time \[\Delta t\]so that the charge reverses its direction crossing the y axis at a distance d. Then:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[B=\frac{mv}{qd}\]and\[\Delta t=\frac{\pi d}{v}\]
done
clear
B)
\[B=\frac{mv}{2qd}\]and\[\Delta t=\frac{\pi d}{2v}\]
done
clear
C)
\[B=\frac{2mv}{qd}\]and\[\Delta t=\frac{\pi d}{2v}\]
done
clear
D)
\[B=\frac{2mv}{qd}\]and\[\Delta t=\frac{\pi d}{v}\]
done
clear
View Answer play_arrow
-
question_answer20) Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \[{{B}_{1}},\] at its centre when a current I passes through it. The ratio \[{{B}_{1}}:{{B}_{2}}\] is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1 : 1
done
clear
B)
1 : 3
done
clear
C)
1 : 9
done
clear
D)
9 : 1
done
clear
View Answer play_arrow
-
question_answer21) A sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
10 cos (500 t)
done
clear
B)
- 10 cos (500t)
done
clear
C)
10 sin (500t)
done
clear
D)
- 10 sin (500t)
done
clear
View Answer play_arrow
-
question_answer22) A lamp emits monochromatic green light uniformly in all directions. The lamp is 3% efficient in converting electrical power to electromagnetic waves and consumes 100 W of power. The amplitude of the electric field associated with the electromagnetic radiation at a distance of 5 m from the lamp will be nearly:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1.34 V/m
done
clear
B)
2.68 V/m
done
clear
C)
4.02 V/m
done
clear
D)
5.36 V/m
done
clear
View Answer play_arrow
-
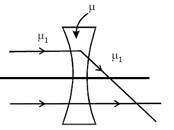
question_answer23) The refractive index of the material of a concave lens is m. It is immersed in a medium of refractive index \[{{\mu }_{1}}.\] A parallel beam of light is incident on the lens. The path of the emergent rays when \[{{\mu }_{1}}>\mu \] is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
question_answer24)
Interference pattern is observed at 'P' due to superimposition of two rays coming out from a source 'S' as shown in the figure. The value of 'l' for which maxima is obtained at 'P' is: (R is perfect reflecting surface) 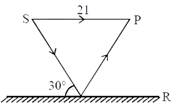 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[1=\frac{1n\lambda }{\sqrt{3}-1}\]
done
clear
B)
\[1=\frac{(2n-1)\lambda }{2\left( \sqrt{3}-1 \right)}\]
done
clear
C)
\[1=\frac{(2n-1)\lambda \sqrt{3}}{4\left( 2-\sqrt{3} \right)}\]
done
clear
D)
\[1=\frac{(2n-1)\lambda }{\sqrt{3}-1}\]
done
clear
View Answer play_arrow
-
question_answer25) In an experiment of single slit diffraction pattern, first minimum for red light coincides with first maximum of some other wavelength. If wavelength of red light is \[\text{6600}\overset{\text{o}}{\mathop{\text{A}}}\,\], then wavelength of first maximum will be:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\text{3300}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[\text{4400}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[\text{5500}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[\text{6600}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
-
question_answer26) A beam of light has two wavelengths of \[\text{497200}\overset{\text{o}}{\mathop{\text{A}}}\,\] and \[\text{6216}\overset{\text{o}}{\mathop{\text{A}}}\,\] with a total intensity of \[3.6\times {{10}^{-3}}W{{m}^{-2}}\] equally distributed among the two wavelengths. The beam falls normally on an area of 1 \[c{{m}^{2}}\] of a clean metallic surface of work function 2.3 eV. Assume that there is no loss of light by reflection and that each capable photon ejects one electron. The number of photoelectrons liberated in 2s is approximately:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[6\times {{10}^{11}}\]
done
clear
B)
\[9\times {{10}^{11}}\]
done
clear
C)
\[11\times {{10}^{11}}\]
done
clear
D)
\[15\times {{10}^{11}}\]
done
clear
View Answer play_arrow
-
question_answer27) A piece of bone of an animal from a ruin is found to have \[^{14}C\] activity of 12 disintegrations per minute per gm of its carbon content. The 14C activity of a living animal is 16 disintegrations per minute per gm. How long ago nearly did the animal die? (Given half life of 14C is t1/2 = 5760 years)
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1672 years
done
clear
B)
2391 years
done
clear
C)
3291 years
done
clear
D)
4453 years
done
clear
View Answer play_arrow
-
question_answer28) For LED's to emit light in visible region of electromagnetic light, it should have energy band gap in the range of:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
eV to 0.4 eV
done
clear
B)
0.5 eV to 0.8 eV
done
clear
C)
0.9 eV to 1.6 eV
done
clear
D)
1.7 eV to 3.0 eV
done
clear
View Answer play_arrow
-
question_answer29) For sky wave propagation, the radio waves must have a frequency range in between:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
MHz to 2 MHz
done
clear
B)
5 MHz to 25 MHz
done
clear
C)
35 MHz to 40 MHz
done
clear
D)
45 MHz to 50 MHz
done
clear
View Answer play_arrow
-
question_answer30) In the experiment of calibration of voltmeter, a standard cell of e.m.f. 1.1 volt is balanced against 440 cm of potential wire. The potential difference across the ends of resistance is found to balance against 220 cm of the wire. The corresponding reading of voltmeter is 0.5 volt. The error in the reading of volmeter will be:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
0. 15 volt
done
clear
B)
0.15 volt
done
clear
C)
0.5 volt
done
clear
D)
? 0.05 volt
done
clear
View Answer play_arrow
-
question_answer31) If m and e are the mass and charge of the revolving electron in the orbit of radius r for hydrogen atom, the total energy of the revolving electron will be:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{1}{2}\frac{{{e}^{2}}}{r}\]
done
clear
B)
\[-\frac{{{e}^{2}}}{r}\]
done
clear
C)
\[m{{e}^{2}}\]
done
clear
D)
\[1\,{{e}^{2}}\]
done
clear
View Answer play_arrow
-
question_answer32) The de-Broglie wavelength of a particle of mass 6.63 g moving with a velocity of 100 \[m{{s}^{-1}}\] is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{10}^{-33}}m\]
done
clear
B)
\[{{10}^{-35}}m\]
done
clear
C)
\[{{10}^{-31}}m\]
done
clear
D)
\[{{10}^{-25}}m\]
done
clear
View Answer play_arrow
-
question_answer33) What happens when an inert gas is added to an equilibrium keeping volume unchanged?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
More product will form
done
clear
B)
Less product will form
done
clear
C)
More reactant will form
done
clear
D)
Equilibrium will remain unchanged
done
clear
View Answer play_arrow
-
question_answer34) The amount of \[BaS{{O}_{4}}\]formed upon mixing 100 mL of 20.8% \[{{H}_{2}}S{{O}_{4}}\] solution with 50 mL of 9.8% \[{{H}_{2}}S{{O}_{4}}\]solution with 50 mL of 9.8% \[{{H}_{2}}S{{O}_{4}}\] solution will be: (Ba = 137, Cl = 35.5, S = 32, H = 1 and O = 16)
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
23.3 g
done
clear
B)
11.65 g
done
clear
C)
30.6 g
done
clear
D)
33.2 g
done
clear
View Answer play_arrow
-
question_answer35) The rate coefficient (k) for a particular reactions is \[1.3\times {{10}^{-4}}{{M}^{-1}}\]\[{{s}^{-1}}\] at \[100{}^\circ C\], and \[1.3\times {{10}^{-3}}\] at \[150{}^\circ C\]. What is the energy of activation (EA) (in kJ) for this reaction? (R = molar gas constant\[=8.31J{{K}^{-1}}kJ\])
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
16
done
clear
B)
60
done
clear
C)
99
done
clear
D)
132
done
clear
View Answer play_arrow
-
question_answer36) How many electrons would be required to deposit 6.35 g of copper at the cathode during the electrolysis of an aqueous solution of copper sulphate? (Atomic mass of copper \[=63.5u,{{N}_{A}}=\] Avogadro's constant):
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{{{N}_{A}}}{20}\]
done
clear
B)
\[\frac{{{N}_{A}}}{10}\]
done
clear
C)
\[\frac{{{N}_{A}}}{5}\]
done
clear
D)
\[\frac{{{N}_{A}}}{2}\]
done
clear
View Answer play_arrow
-
question_answer37) The \[\left( S{}^\circ \right)\] of the following substances are: \[C{{H}_{4}}(g)186.2J{{K}^{-1}}mo{{l}^{-1}}\] \[{{O}_{2}}(g)205.2J{{K}^{-1}}mo{{l}^{-1}}\] \[{{H}_{2}}O(g)69.9J{{K}^{-1}}mo{{l}^{-1}}\] The entropy change \[(\Delta {{S}^{o}})\]for the reaction : \[C{{H}_{4}}(g)+2{{O}_{2}}(g)\to C{{O}_{2}}(g)+2{{H}_{2}}O(l)\]is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[-312.5J{{K}^{-1}}mo{{l}^{-1}}\]
done
clear
B)
\[-242.8J{{K}^{-1}}mo{{l}^{-1}}\]
done
clear
C)
\[-108.1J{{K}^{-1}}mo{{l}^{-1}}\]
done
clear
D)
\[-37.6J{{K}^{-1}}mo{{l}^{-1}}\]
done
clear
View Answer play_arrow
-
question_answer38) The conjugate base of hydrazoic acid is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{N}^{-3}}\]
done
clear
B)
\[N_{3}^{-}\]
done
clear
C)
\[N_{2}^{-}\]
done
clear
D)
\[HN_{3}^{-}\]
done
clear
View Answer play_arrow
-
question_answer39) In a monoclinic unit cell, the relation of sides and angles are respectively:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[a=b\ne c\]and \[\alpha =\beta =\gamma ={{90}^{o}}\]
done
clear
B)
\[a\ne b\ne c\]and \[\alpha =\beta =\gamma ={{90}^{o}}\]
done
clear
C)
\[a\ne b\ne c\]and \[\beta =\gamma ={{90}^{o}}\ne \alpha \]
done
clear
D)
\[a\ne b\ne c\]and \[\alpha \ne \beta \ne \gamma \ne {{90}^{o}}\]
done
clear
View Answer play_arrow
-
question_answer40) The standard enthalpy of formation \[({{\Delta }_{f}}{{H}^{o}}_{298})\]for methane, \[C{{H}_{4}}\]is\[-74.9kJ\,mo{{l}^{-1}}.\]In order to calculate the average energy given out in the formation of a C ? H bond from this it is necessary to know which one of the following?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
The dissociation energy of the hydrogen molecule, \[{{H}_{2}}\].
done
clear
B)
The first four ionisation energies of carbon.
done
clear
C)
The dissociation energy of \[{{H}_{2}}\]and enthalpy and sublimation of carbon (graphite).
done
clear
D)
The first four ionisation energies of carbon and electron affinity of hydrogen.
done
clear
View Answer play_arrow
-
question_answer41) Which of the following xenon-oxo compounds may not be obtained by hydrolysis of xenon fluorides?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[Xe{{O}_{2}}{{F}_{2}}\]
done
clear
B)
\[XeO{{F}_{4}}\]
done
clear
C)
\[Xe{{O}_{3}}\]
done
clear
D)
\[Xe{{O}_{4}}\]
done
clear
View Answer play_arrow
-
question_answer42) Excited hydrogen atom emits light in the ultraviolet region at \[2.47\times {{10}^{15}}Hz.\]With this frequency, the energy of a single photon is: \[(h=6.63\times {{10}^{-34}}Js)\]
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[8.041\times {{10}^{-40}}J\]
done
clear
B)
\[2.680\times {{10}^{-19}}J\]
done
clear
C)
\[1.640\times {{10}^{-18}}J\]
done
clear
D)
\[6.111\times {{10}^{-17}}J\]
done
clear
View Answer play_arrow
-
question_answer43) Which one of the following exhibits the large number of oxidation states?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Ti (22)
done
clear
B)
V (23)
done
clear
C)
Cr (24)
done
clear
D)
Mn (25)
done
clear
View Answer play_arrow
-
question_answer44) Copper becomes green when exposed to moist air for a long period. This is due to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
the formation of a layer of cupric oxide on the surface of copper.
done
clear
B)
the formation of a layer of basic carbonate of copper on the surface of copper.
done
clear
C)
the formation of a layer of cupric hydroxide on the surface of copper.
done
clear
D)
the formation of basic copper sulphate layer on the surface of the metal.
done
clear
View Answer play_arrow
-
question_answer45) Among the following species the one which causes the highest \[CFSE,{{\Delta }_{0}}\]as a ligand is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[C{{N}^{-}}\]
done
clear
B)
\[N{{H}_{3}}\]
done
clear
C)
\[{{F}^{-}}\]
done
clear
D)
CO
done
clear
View Answer play_arrow
-
question_answer46) Similarity in chemical properties of the atoms of elements in a group of the Periodic table is most closely related to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
atomic numbers
done
clear
B)
atomic masses
done
clear
C)
number of principal energy levels
done
clear
D)
number of valence electrons
done
clear
View Answer play_arrow
-
question_answer47) Which of the following arrangements represents the increasing order (smallest to largest) of ionic radii of the given species \[{{O}^{2-}},{{S}^{2-}},{{N}^{3-}},{{p}^{3-?}}\]
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{O}^{2-}}<{{N}^{3-}}<{{S}^{2-}}<{{p}^{3-}}\]
done
clear
B)
\[{{O}^{2-}}<{{p}^{3-}}<{{N}^{3-}}<{{S}^{2-}}\]
done
clear
C)
\[{{N}^{3}}<{{O}^{2-}}<{{p}^{3-}}<{{S}^{2-}}\]
done
clear
D)
\[{{N}^{3-}}<{{S}^{2-}}<{{O}^{2-}}<{{p}^{3-}}\]
done
clear
View Answer play_arrow
-
question_answer48) Global warming is due to increase of:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
methane and nitrous oxide in atmosphere
done
clear
B)
methane and \[C{{O}_{2}}\] in atmosphere
done
clear
C)
methane and \[{{O}_{3}}\] in atmosphere
done
clear
D)
methane and CO in atmosphere
done
clear
View Answer play_arrow
-
question_answer49) Hydrogen peroxide acts both as an oxidising and as a reducing agent depending upon the nature of the reacting species. In which of the following cases \[{{H}_{2}}{{O}_{2}}\]acts as a reducing agent in acid medium?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[MnO_{4}^{-}\]
done
clear
B)
\[C{{r}_{2}}O_{7}^{2-}\]
done
clear
C)
\[SO_{3}^{2-}\]
done
clear
D)
KI
done
clear
View Answer play_arrow
-
question_answer50) Which one of the following complexes will most likely absorb visible light? (At nos. Sc = 21, Ti = 22, V = 23, Zn = 30)
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{[Sc{{({{H}_{2}}O)}_{6}}]}^{3+}}\]
done
clear
B)
\[{{[Ti{{(N{{H}_{3}})}_{6}}]}^{4+}}\]
done
clear
C)
\[{{[V{{(N{{H}_{3}})}_{6}}]}^{3+}}\]
done
clear
D)
\[{{[Zn{{(N{{H}_{3}})}_{6}}]}^{2+}}\]
done
clear
View Answer play_arrow
-
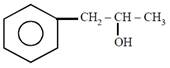
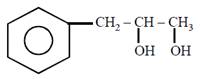
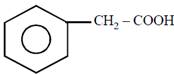
question_answer51)
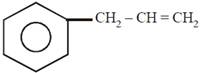 on mercuration-demercuration produces the major product:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
on mercuration-demercuration produces the major product:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
question_answer52) In the Victor-Meyer's test, the colour given by \[1{}^\circ ,\text{ }2{}^\circ \text{ }and\text{ }3{}^\circ \] alcohols are respectively:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Red, colourless, blue
done
clear
B)
Red, blue, colourless
done
clear
C)
Colourless, red, blue
done
clear
D)
Red, blue, violet
done
clear
View Answer play_arrow
-
question_answer53) Conversion of benzene diazonium chloride to chlorobenzene is an example of which of the following reactions?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Claisen
done
clear
B)
Friedel-craft
done
clear
C)
Sandmeyer
done
clear
D)
Wurtz
done
clear
View Answer play_arrow
-
question_answer54) In the presence of peroxide, HCl and HI do not give anti- Markownikoff's addition of alkenes because:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
One of the steps is endothermic in HCl and HI
done
clear
B)
Both HCl and HI are strong acids
done
clear
C)
HCl is oxidizing and the HI is reducing
done
clear
D)
All the steps are exothermic is HCl and HI
done
clear
View Answer play_arrow
-
question_answer55) The major product obtained in the photo catalyzed bromination of 2--methylbutane is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1-bromo-2-methylbutane
done
clear
B)
1-bromo-3-methylbutane
done
clear
C)
2-bromo-3-methylbutane
done
clear
D)
2-bromo-2-methylbutane
done
clear
View Answer play_arrow
-
question_answer56) Which of the following molecules has two sigma (s) and two \[{{p}_{i}}(\pi )\]bonds?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[{{C}_{2}}{{H}_{4}}\]
done
clear
B)
\[{{N}_{2}}{{F}_{2}}\]
done
clear
C)
\[{{C}_{2}}{{H}_{2}}C{{l}_{2}}\]
done
clear
D)
HCN
done
clear
View Answer play_arrow
-
question_answer57) Which one of the following acids does not exhibit optical isomerism?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Lactic acid
done
clear
B)
Tartaric acid
done
clear
C)
Maleic acid
done
clear
D)
\[\text{ }\!\!\alpha\!\!\text{ -}\]amino acids
done
clear
View Answer play_arrow
-
question_answer58) Aminoglycosides are usually used as:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
antibiotic
done
clear
B)
analgesic
done
clear
C)
hypnotic
done
clear
D)
antifertility
done
clear
View Answer play_arrow
-
question_answer59) Which of the following will not show mutarotation?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Maltose
done
clear
B)
Lactose
done
clear
C)
Glucose
done
clear
D)
Sucrose
done
clear
View Answer play_arrow
-
question_answer60) Phthalic acid reacts with resorcinol in the presence of concentrated \[{{H}_{2}}S{{O}_{4}}\]to give:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Phenolphthalein
done
clear
B)
Alizarin
done
clear
C)
Coumarin
done
clear
D)
Fluorescein
done
clear
View Answer play_arrow
-
question_answer61) A relation on the set \[a=\{x:|x|<3,x\in Z\},\]where Z is the set of integers is defined by \[R=\{x,y):y=|x|,x\ne -1\}.\]Then the number of elements in the power set of R is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
32
done
clear
B)
16
done
clear
C)
8
done
clear
D)
64
done
clear
View Answer play_arrow
-
question_answer62) Let \[z\ne -i\] be any complex number such that \[\frac{z-i}{z+i}\]is a purely imaginary number. Then\[z+\frac{1}{z}\]is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
0
done
clear
B)
any non-zero real number other than 1.
done
clear
C)
any non-zero real number.
done
clear
D)
a purely imaginary number.
done
clear
View Answer play_arrow
-
question_answer63) The sum of the roots of the equation, \[{{x}^{2}}+|2x-3|-4=0,\] is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[2\]
done
clear
B)
\[-2\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[-\sqrt{2}\]
done
clear
View Answer play_arrow
-
question_answer64) If \[\left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ {{(a+\lambda )}^{2}} & {{(b+\lambda )}^{2}} & {{(a+\lambda )}^{2}} \\ {{(a-\lambda )}^{2}} & {{(b-\lambda )}^{2}} & {{(c+\lambda )}^{2}} \\ \end{matrix} \right|=\] \[k\lambda \left| \begin{matrix} {{a}^{2}} & {{b}^{2}} & {{c}^{2}} \\ a & b & c \\ 1 & 1 & 1 \\ \end{matrix} \right|,\lambda \ne 0\]then k is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[4\lambda abc\]
done
clear
B)
\[-4\lambda abc\]
done
clear
C)
\[4{{\lambda }^{2}}\]
done
clear
D)
\[-4{{\lambda }^{2}}\]
done
clear
View Answer play_arrow
-
question_answer65) If\[A=\left[ \begin{matrix} 1 & 2 & x \\ 3 & -1 & 2 \\ \end{matrix} \right]\]and\[B=\left[ \begin{align} & y \\ & x \\ & 1 \\ \end{align} \right]\]be such that\[AB=\left[ \begin{align} & 6 \\ & 8 \\ \end{align} \right],\]then:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[y=2x\]
done
clear
B)
\[y=2x\]
done
clear
C)
\[y=x\]
done
clear
D)
\[y=-x\]
done
clear
View Answer play_arrow
-
question_answer66) 8-digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do no occupy odd places, is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
160
done
clear
B)
120
done
clear
C)
60
done
clear
D)
48
done
clear
View Answer play_arrow
-
question_answer67) If\[{{\left( 2+\frac{x}{3} \right)}^{55}}\]is expanded in the ascending powers of x and the coefficients of powers of x in two consecutive terms of the expansion are equal, then these terms are:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
7th and 8th
done
clear
B)
8th and 9th
done
clear
C)
28th and 29th
done
clear
D)
27th and 28th
done
clear
View Answer play_arrow
-
question_answer68) Let G be the geometric mean of two positive numbers a and b, and M be the arithmetic mean of \[\frac{1}{a}\]and\[\frac{1}{b}.\]If\[\frac{1}{M}:G\]is 4 : 5 then a : b can be:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
1 : 4
done
clear
B)
1 : 2
done
clear
C)
2 : 3
done
clear
D)
3 : 4
done
clear
View Answer play_arrow
-
question_answer69) The least positive integer n such that \[1-\frac{2}{3}-\frac{2}{{{3}^{2}}}-....-\frac{2}{{{3}^{n-1}}}<\frac{1}{100},\]is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
4
done
clear
B)
5
done
clear
C)
7
done
clear
D)
7
done
clear
View Answer play_arrow
-
question_answer70) Let \[f,g:R\to R\]be two functions defined by \[f(x)=\left\{ \begin{align} & x\sin \left( \frac{1}{x} \right),x\ne 0 \\ & 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,x=0 \\ \end{align} \right.,\]and \[g(x)=xf(x)\] Statement I: f is a continuous function at x = 0. Statement II: g is a differentiable function at x = 0.
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Both statement I and II are false.
done
clear
B)
Both statement I and II are true.
done
clear
C)
Statement I is true, statement II is false.
done
clear
D)
Statement I is false, statement II is true.
done
clear
View Answer play_arrow
-
question_answer71) If \[f(x)={{x}^{2}}-x+5,x>\frac{1}{2},\]and g(x) is its inverse function, then g'(7) equals:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[-\frac{1}{3}\]
done
clear
B)
\[\frac{1}{13}\]
done
clear
C)
\[\frac{1}{3}\]
done
clear
D)
\[-\frac{1}{13}\]
done
clear
View Answer play_arrow
-
question_answer72) Let f and g be two differentiable functions on R such that f'(x) > 0 and g'(x) < 0 for all \[x\in R\]. Then for all x:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
f (g (x)) > f (g (x - 1))
done
clear
B)
f (g (x)) > f (g (x + 1))
done
clear
C)
g(f (x)) > g (f (x - 1))
done
clear
D)
g(f (x)) < g (f (x + 1))
done
clear
View Answer play_arrow
-
question_answer73) If \[1+{{x}^{4}}+{{x}^{5}}=T\sum\limits_{i=0}^{5}{{{a}_{i}}}{{\left( 1+x \right)}^{i}},\]for all x in R, then \[{{a}_{2}}\]is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
-4
done
clear
B)
6
done
clear
C)
-8
done
clear
D)
10
done
clear
View Answer play_arrow
-
question_answer74) The integral \[\int_{{}}^{{}}{\frac{\sin x{{\cos }^{2}}x}{{{\left( {{\sin }^{3}}x+{{\cos }^{3}}x \right)}^{2}}}dx}\]is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{1}{\left( 1+{{\cot }^{3}}x \right)}+c\]
done
clear
B)
\[-\frac{1}{3\left( 1+{{\cot }^{3}}x \right)}+c\]
done
clear
C)
\[-\frac{{{\sin }^{3}}x}{\left( 1+{{\cot }^{3}}x \right)}+c\]
done
clear
D)
\[-\frac{{{\cos }^{3}}x}{3\left( 1+{{\cot }^{3}}x \right)}+c\]
done
clear
View Answer play_arrow
-
question_answer75) If [ ] denotes the greatest integer function, then the integral \[\int\limits_{0}^{\pi }{\left[ \cos x \right]}dx\]is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{\pi }{2}\]
done
clear
B)
0
done
clear
C)
-1
done
clear
D)
\[-\frac{\pi }{2}\]
done
clear
View Answer play_arrow
-
question_answer76) If for a continuous function \[f(x),\int\limits_{-\pi }^{t}{\left( f\left( x \right)+x \right)dx}={{\pi }^{2}}-t2,\]for all\[t\ge -\pi ,\]then\[\left( -\frac{\pi }{3} \right)\]is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\frac{\pi }{3}\]
done
clear
D)
\[\frac{\pi }{6}\]
done
clear
View Answer play_arrow
-
question_answer77) The general solution of the differential equation, \[\sin 2x\left( \frac{dy}{dx}-\sqrt{\tan x} \right)-y=0,\]is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[y\sqrt{\tan x}=x+c\]
done
clear
B)
\[y\sqrt{\cot x}=\tan x+c\]
done
clear
C)
\[y\sqrt{\tan x}=\cot x+c\]
done
clear
D)
\[y\sqrt{\cot x}=x+c\]
done
clear
View Answer play_arrow
-
question_answer78) If a line intercepted between the coordinate axes is trisected at a point A(4, 3), which is nearer to x-axis, then its equation is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[4x\text{ }-\text{ }3y\text{ }=\text{ }7\text{ }~\]
done
clear
B)
\[3x\text{ }+\text{ }2y\text{ }=\text{ }18\]
done
clear
C)
\[3x\text{ }+\text{ }8y\text{ }=\text{ }36\]
done
clear
D)
\[x\text{ }+\text{ }3y\text{ }=\text{ }13\]
done
clear
View Answer play_arrow
-
question_answer79) If the three distinct lines x + 2ay + a = 0, x + 3by + b = 0 and x + 4ay + a = 0 are concurrent, then the point (a, b) lies on a:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
circle
done
clear
B)
hyperbola
done
clear
C)
straight line
done
clear
D)
parabola
done
clear
View Answer play_arrow
-
question_answer80) For the two circles \[{{x}^{2}}+{{y}^{2}}=16\] and \[{{x}^{2}}+{{y}^{2}}-2y=0,\]there is/are
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
one pair of common tangents
done
clear
B)
two pair of common tangents
done
clear
C)
three pair of common tangents
done
clear
D)
no common tangent
done
clear
View Answer play_arrow
-
question_answer81) Two tangents are drawn from a point (- 2, - 1) to the curve, \[{{y}^{2}}=4x.\] If \[\alpha \] is the angle between them, then \[|\tan \alpha |\]is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{1}{\sqrt{3}}\]
done
clear
C)
\[\sqrt{3}\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
-
question_answer82) The minimum area of a triangle formed by any tangent to the ellipse\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{81}=1\]and the co-ordinate axes is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
12
done
clear
B)
18
done
clear
C)
26
done
clear
D)
36
done
clear
View Answer play_arrow
-
question_answer83) A symmetrical form of the line of intersection of the planes \[x\text{ }=\text{ }ay\text{ }+\text{ }b\text{ }and\text{ }z\text{ }=\text{ }cy\text{ }+\text{ }d\] is
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{x-b}{a}+\frac{y-1}{1}=\frac{z-d}{c}\]
done
clear
B)
\[\frac{x-b-a}{a}=\frac{y-1}{1}=\frac{z-d-c}{c}\]
done
clear
C)
\[\frac{x-a}{b}=\frac{y-0}{1}=\frac{z-c}{d}\]
done
clear
D)
\[\frac{x-b-a}{b}=\frac{y-1}{0}=\frac{z-d-c}{d}\]
done
clear
View Answer play_arrow
-
question_answer84) If the distance between planes, \[4x-2y-4z+1=0\]and \[2y-4z+d=0\] is 7, then d is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[41 or - 42\]
done
clear
B)
\[42 or - 43\]
done
clear
C)
\[- 41 or 43\]
done
clear
D)
\[- 42 or 44\]
done
clear
View Answer play_arrow
-
question_answer85) If \[\hat{x},\hat{y}\]and \[\hat{z}\] are three unit vectors in three-dimensional space, then the minimum value of\[|\hat{x}+\hat{y}{{|}^{2}}+|\hat{y}+\hat{z}{{|}^{2}}+|\hat{z}+\hat{x}{{|}^{2}}\]
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\frac{3}{2}\]
done
clear
B)
3
done
clear
C)
\[3\sqrt{3}\]
done
clear
D)
6
done
clear
View Answer play_arrow
-
question_answer86) Let\[\overline{X}\]and M.D. be the mean and the mean deviation about X of n observations \[{{x}_{i}},\] i = 1, 2, ........, n. If each of the observations is increased by 5, then the new mean and the mean deviation about the new mean, respectively, are :
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\overline{X},M.D.\]
done
clear
B)
\[\overline{X}+5,M.D.\]
done
clear
C)
\[\overline{X},M.D.+5\]
done
clear
D)
\[\overline{X}+M.D.+5\]
done
clear
View Answer play_arrow
-
question_answer87) A number x is chosen at random from the set {1, 2, 3, 4, ...., 100}. Define the event: A = the chosen number x satisfies\[\frac{\left( x-10 \right)\left( x-50 \right)}{\left( x-30 \right)}\ge 0\] Then P (A) is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
0.71
done
clear
B)
0.70
done
clear
C)
0.51
done
clear
D)
0.20
done
clear
View Answer play_arrow
-
question_answer88) Statement I : The equation\[{{(si{{n}^{-1}}x)}^{3}}+\]\[{{(co{{s}^{-1}}x)}^{3}}+a{{\pi }^{3}}=0\]has a solution for all\[a\ge \frac{1}{32}.\] Statement II: For any \[x\in R,\] \[{{\sin }^{-1}}x{{\cos }^{-1}}x=\frac{\pi }{C}\]and\[0\le {{\left( {{\sin }^{-1}}x-\frac{\pi }{4} \right)}^{2}}\le \frac{9{{\pi }^{2}}}{16}\]
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
Both statements I and II are true.
done
clear
B)
Both statements I and II are false.
done
clear
C)
Statement I is true and statement II is false.
done
clear
D)
Statement I is false and statement II is true.
done
clear
View Answer play_arrow
-
question_answer89) If \[f(\theta )=\left| \begin{matrix} 1 & \cos \theta & 1 \\ -\sin \theta & 1 & -\cos \theta \\ -1 & \sin \theta & 1 \\ \end{matrix} \right|\]and A and B are respectively the maximum and the minimum values of f(q), then (A, B) is equal to:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[(3, - 1)\]
done
clear
B)
\[\left( 4,2-\sqrt{2} \right)\]
done
clear
C)
\[\left( 2+\sqrt{2},2-\sqrt{2} \right)\]
done
clear
D)
\[\left( 2+\sqrt{2},-1 \right)\]
done
clear
View Answer play_arrow
-
question_answer90) Let p, q, r denote arbitrary statements. Then the logically equivalent of the statement\[p\Rightarrow \left( q\vee r \right)\] is:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
A)
\[\left( p\vee q \right)\Rightarrow r\]
done
clear
B)
\[\left( p\Rightarrow q \right)\vee \left( p\Rightarrow r \right)\]
done
clear
C)
\[\left( p\Rightarrow \tilde{\ }q \right)\wedge \left( p\Rightarrow r \right)\]
done
clear
D)
\[\left( p\Rightarrow q \right)\wedge \left( p\Rightarrow \tilde{\ }r \right)\]
done
clear
View Answer play_arrow
 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
 Two hypothetical planets of masses m1 and m2 are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ?d?? (Speed of \[{{m}_{1}}\] is \[{{v}_{1}}\] and that of \[{{m}_{2}}\] is \[{{v}_{2}}\])
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
Two hypothetical planets of masses m1 and m2 are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ?d?? (Speed of \[{{m}_{1}}\] is \[{{v}_{1}}\] and that of \[{{m}_{2}}\] is \[{{v}_{2}}\])
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
 How much is the current I in the circuit in steady state?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
How much is the current I in the circuit in steady state?
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
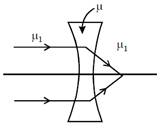
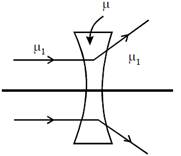
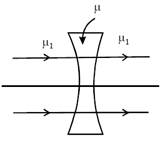
 [JEE Main Online Paper ( Held On 12 Apirl 2014 )
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
 on mercuration-demercuration produces the major product:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )
on mercuration-demercuration produces the major product:
[JEE Main Online Paper ( Held On 12 Apirl 2014 )