Solved papers for JEE Main & Advanced Physics Simple Harmonic Motion JEE PYQ-Simple Harmonic Motion

done JEE PYQ-Simple Harmonic Motion Total Questions - 76

• question_answer1) In a simple harmonic oscillator, at the mean position                                              [AIEEE 2002]
  A)
   kinetic energy is minimum, potential energy is maximum
  done clear
  B)
   both kinetic and potential energies are maximum
  done clear
  C)
   kinetic energy is maximum, potential energy is minimum
  done clear
  D)
   both kinetic and potential energies are minimum 
  done clear
  View Answer play_arrow

• question_answer2) A child swinging on a swing in sitting position, stands up, then the time period of the swing will  [AIEEE 2002]
  A)
   increase                       
  done clear
  B)
   decrease
  done clear
  C)
   remain same
  done clear
  D)
                                                           increase if the child is long and decrease if the child is short                                             
  done clear
  View Answer play_arrow

• question_answer3) A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes \[5T/3\], then the ratio of \[\frac{m}{M}\] is                                                                                  [AIEEE 2003]
  A)
   \[\frac{3}{5}\]             
  done clear
  B)
        \[\frac{25}{9}\]
  done clear
  C)
   \[\frac{16}{9}\]            
  done clear
  D)
        \[\frac{5}{3}\]
  done clear
  View Answer play_arrow

• question_answer4) Two particles A and B of equal masses are suspended from two massless springs of spring constants \[{{k}_{1}}\] and \[{{k}_{2}}\], respectively. If the   maximum   velocities,   during oscillations are equal, the ratio of amplitudes of A and B is            [AIEEE 2003]
  A)
   \[\sqrt{{{k}_{1}}/{{k}_{2}}}\]         
  done clear
  B)
        \[{{k}_{1}}/{{k}_{2}}\]
  done clear
  C)
   \[\sqrt{{{k}_{2}}/{{k}_{1}}}\]  
  done clear
  D)
        \[{{k}_{2}}/{{k}_{1}}\] \[\]
  done clear
  View Answer play_arrow

• question_answer5) The length of a simple pendulum executing simple harmonic motion is increased by 21%. The percentage increase in the time period of the pendulum of increased length is                                                                      [AIEEE 2003]
  A)
   \[11%\]            
  done clear
  B)
        \[21%\]
  done clear
  C)
   \[42%\]
  done clear
  D)
        \[10.5%\]
  done clear
  View Answer play_arrow

• question_answer6) The displacement of a particle varies according to the relation\[x=4\,(\cos \pi \,t+\sin \pi t)\]. The amplitude of the particle is          [AIEEE 2003]
  A)
   \[-4\]               
  done clear
  B)
        4
  done clear
  C)
   \[4\sqrt{2}\]     
  done clear
  D)
        8
  done clear
  View Answer play_arrow

• question_answer7)   A body executes simple harmonic motion. The potential energy (PE), the kinetic energy (KE) and total energy (TE) are measured as function of displacement\[x\]. Which of the following statements is true?               [AIEEE 2003]
  A)
   KE is maximum when \[x=0\]
  done clear
  B)
   TE is zero when \[x=0\]
  done clear
  C)
   KE is maximum when \[x\] is maximum
  done clear
  D)
   PE is maximum when \[x=0\]
  done clear
  View Answer play_arrow

• question_answer8) The total energy of a particle, executing simple harmonic motion is               [AIEEE 2004]
  A)
   \[\propto x\]                 
  done clear
  B)
        \[\propto \,{{x}^{2}}\]
  done clear
  C)
   Independent of\[x.\]
  done clear
  D)
   \[\propto {{x}^{1/2}}\] where,\[x\]is the displacement from the mean position.
  done clear
  View Answer play_arrow

• question_answer9) A particle of mass m is attached to a spring (of spring constant\[k\] and has a natural angular frequency\[{{\omega }_{0}}\]. An external force F(t) proportional to \[\cos \omega t(\omega \ne {{\omega }_{0}})\]is applied to the oscillator. The time displacement of the oscillator will be proportional to [AIEEE 2004]
  A)
   \[\frac{m}{\omega _{0}^{2}-{{\omega }^{2}}}\]        
  done clear
  B)
        \[\frac{1}{m(\omega _{0}^{2}-{{\omega }^{2}})}\]
  done clear
  C)
   \[\frac{1}{m(\omega _{0}^{2}+{{\omega }^{2}})}\]  
  done clear
  D)
        \[\frac{m}{\omega _{0}^{2}+{{\omega }^{2}}}\]
  done clear
  View Answer play_arrow

• question_answer10) In forced oscillation of a particle, the amplitude is maximum for a frequency\[{{\omega }_{1}}\]of the force, while the energy is maximum for a frequency \[{{\omega }_{2}}\]of the force, then                            [AIEEE 2004]
  A)
   \[{{\omega }_{1}}={{\omega }_{2}}\]
  done clear
  B)
   \[{{\omega }_{1}}>{{\omega }_{2}}\]
  done clear
  C)
  \[{{\omega }_{1}}<{{\omega }_{2}}\]when damping is small and\[{{\omega }_{1}}>{{\omega }_{2}}\] when damping is large
  done clear
  D)
   \[{{\omega }_{1}}<{{\omega }_{2}}\]
  done clear
  View Answer play_arrow

• question_answer11) The function\[\sin (\omega t)\]represents                                                                 [AIEEE 2005]
  A)
   a periodic, but not simple harmonic motion with a period \[2\pi /\omega \]
  done clear
  B)
   a periodic, but not simple harmonic motion with a period \[\pi /\omega \]
  done clear
  C)
   a simple harmonic motion with a period \[2\pi /\omega \]
  done clear
  D)
   a simple harmonic motion with a period \[\pi /\omega \]
  done clear
  View Answer play_arrow

• question_answer12) Two simple harmonic motions are represented    by    the    equations \[{{y}_{1}}=0.1\sin \left( 100\pi t+\frac{\pi }{3} \right)\]and\[{{y}_{2}}=0.1\,\cos \pi t.\] The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is                          [AIEEE 2005]
  A)
   \[\frac{-\pi }{6}\]            
  done clear
  B)
      \[\frac{\pi }{3}\]
  done clear
  C)
   \[\frac{-\pi }{3}\]              
  done clear
  D)
        \[\frac{\pi }{6}\]
  done clear
  View Answer play_arrow

• question_answer13) If a simple harmonic motion is represented by \[\frac{{{d}^{2}}x}{d{{t}^{2}}}+\alpha x=0,\] its time period is                              [AIEEE 2005]
  A)
   \[\frac{2\pi }{\alpha }\]             
  done clear
  B)
       \[\frac{2\pi }{\sqrt{\alpha }}\]  
  done clear
  C)
   \[2\pi \alpha \] 
  done clear
  D)
        \[2\pi \sqrt{\alpha }\]
  done clear
  View Answer play_arrow

• question_answer14) The bob of a simple pendulum is a spherical hollow ball filled with water. A plugged hole near the bottom of the oscillating bob gets suddenly unplugged. During observation, till water is coming out, the time period of oscillation would [AIEEE 2005]
  A)
   first increase and then decrease to the original value
  done clear
  B)
   first decrease and then increase to the original value
  done clear
  C)
   remain unchanged
  done clear
  D)
   increase towards a saturation value
  done clear
  View Answer play_arrow

• question_answer15) The maximum velocity of a particle, executing simple harmonic motion with an amplitude 7 mm, is 4.4 m/s. The period of oscillation is                                                                                                                   [AIEEE 2006]
  A)
   0.01s      
  done clear
  B)
        10s
  done clear
  C)
   0.1s                
  done clear
  D)
        100s
  done clear
  View Answer play_arrow

• question_answer16) Starting from the origin, a body oscillates simple harmonically with a period of 2 s. After what time will its kinetic energy be 75% of the total energy?                                                                                                 [AIEEE 2006]
  A)
   \[\frac{1}{6}s\]           
  done clear
  B)
        \[\frac{1}{4}s\]
  done clear
  C)
   \[\frac{1}{3}s\]            
  done clear
  D)
        \[\frac{1}{12}s\]
  done clear
  View Answer play_arrow

• question_answer17) A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency\[\omega \]. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time [AIEEE 2006]
  A)
   at the mean position of the platform
  done clear
  B)
   for an amplitude of \[g/{{\omega }^{2}}\]
  done clear
  C)
   for an amplitude of\[{{g}^{2}}/{{\omega }^{2}}\]
  done clear
  D)
   at the highest position of the platform
  done clear
  View Answer play_arrow

• question_answer18) The displacement of an object attached to a spring and executing simple harmonic motion is given by\[2x+3y+z=1\]\[x+3y+2z=2\] metre. The time at which the maximum speed first occurs is [AIEEE 2007]
  A)
   0.5 s           
  done clear
  B)
        0.75 s
  done clear
  C)
   0.125s          
  done clear
  D)
                    0.25s
  done clear
  View Answer play_arrow

• question_answer19) A point mass oscillates along the x-axis according to the law\[{{\log }_{3}}e\].If the acceleration of the particle is written as \[{{\log }_{e}}3\]then                                                                               [AIEEE 2007]
  A)
   \[f(x)={{\tan }^{-1}}(\sin x+\cos x)\]
  done clear
  B)
        \[(\pi /4,\pi /2)\]
  done clear
  C)
   \[(-\pi /2,\pi /4)\]
  done clear
  D)
   \[(0,\pi /2)\]
  done clear
  View Answer play_arrow

• question_answer20) 

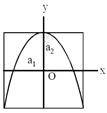
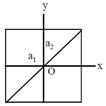
  Two springs, of force constants\[{{I}_{0}}=\frac{E}{R}=\frac{5}{5}=1\,A\]and\[\tau =\frac{L}{R}=\frac{10}{5}=2\,s\]are connected to a mass m as shown. The frequency of oscillation of the mass is\[t=2s\]. If\[I=(1-{{e}^{-1}})A\]both\[(\therefore -t/\tau =\frac{-2}{2}=-1)\]and\[J=\frac{i}{\pi {{a}^{2}}}\]are made four times their original values, the frequency of. oscillation becomes    [AIEEE 2007]

  A)
   \[\oint{B.dl}={{\mu }_{0}}.{{i}_{enclosed}}\]              
  done clear
  B)
        \[\oint{B.dl}={{\mu }_{0}}.{{i}_{enclosed}}\]     
  done clear
  C)
   \[x=2\times {{10}^{-2}}\]                   
  done clear
  D)
        \[cos\text{ }\pi t\]
  done clear
  View Answer play_arrow

• question_answer21) A particle of mass m executes simple harmonic motion with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilibrium to the end is                                                            [AIEEE 2007]
  A)
   \[p=\frac{{{E}_{0}}{{I}_{0}}}{2}\]
  done clear
  B)
        \[P=\sqrt{2}{{E}_{0}}{{I}_{0}}\]
  done clear
  C)
   \[{{10}^{-3}}\mu C\]      
  done clear
  D)
        \[(\sqrt{2},\sqrt{2})\]
  done clear
  View Answer play_arrow

• question_answer22) If\[x,\text{ v}\]and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?                  [AIEEE 2009]
  A)
   \[{{a}^{2}}{{T}^{2}}+4{{\pi }^{2}}{{v}^{2}}\]
  done clear
  B)
        \[aT/x\]
  done clear
  C)
   \[aT+2\pi v\]    
  done clear
  D)
        \[aT/v.\]
  done clear
  View Answer play_arrow

• question_answer23) A mass M, attached to a horizontal spring, executes S.H.M. with amplitude \[{{A}_{1}}\]. When the mass M passes through its mean position then a smaller mass m is placed over it and both of them move together with amplitude \[{{A}_{2}}\]. The ratio of\[\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)\]is                       [AIEEE 2011]
  A)
   \[{{\left( \frac{M+m}{M} \right)}^{1/2}}\]       
  done clear
  B)
        \[\frac{M}{M+m}\]
  done clear
  C)
   \[\frac{M+m}{M}\]      
  done clear
  D)
        \[{{\left( \frac{M}{M+m} \right)}^{1/2}}\]
  done clear
  View Answer play_arrow

• question_answer24) Two particles are executing simple harmonic motion of the same amplitude A and frequency \[\omega \] along the x-axis. Their mean position is separated by distance \[{{X}_{0}}({{X}_{0}}>A)\]. If the maximum separation between them is  \[({{X}_{0}}+A)\], the phase difference between their motion is                             [AIEEE 2011]
  A)
   \[\frac{\pi }{6}\]           
  done clear
  B)
                    \[\frac{\pi }{2}\]
  done clear
  C)
   \[\frac{\pi }{3}\]           
  done clear
  D)
        \[\frac{\pi }{4}\]
  done clear
  View Answer play_arrow

• question_answer25) A wooden cube (density of wood ‘d’) of side \['\ell '\] floats in a liquid of density\['\rho '\] with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T'. Then, T is equal to:                                                                                                                         [AIEEE 11-05-2011]
  A)
  \[2\pi \sqrt{\frac{\ell d}{\rho g}}\]
  done clear
  B)
                   \[2\pi \sqrt{\frac{\ell \rho }{dg}}\]
  done clear
  C)
  \[2\pi \sqrt{\frac{\ell d}{(\rho -d)g}}\]
  done clear
  D)
       \[2\pi \sqrt{\frac{\ell \rho }{(\rho -d)g}}\]
  done clear
  View Answer play_arrow

• question_answer26) The displacement \[y(t)=A\sin (\omega t+\phi )\] of a pendulum for \[\phi =\frac{2\pi }{3}\] is correctly represented by [JEE ONLINE 19-05-2012]
  A)
   
  done clear
  B)
        
  done clear
  C)
   
  done clear
  D)
        
  done clear
  View Answer play_arrow

• question_answer27) 

  A ring is suspended from a point S on its rim as shown in the figure. When displaced from equilibrium, it oscillates with time period of 1 second. The radius of the ring is (take \[g={{\pi }^{2}}\])          [JEE ONLINE 19-05-2012]

  A)
   0.15m        
  done clear
  B)
        1.5m
  done clear
  C)
   1.0m               
  done clear
  D)
        0.5m
  done clear
  View Answer play_arrow

• question_answer28) The amplitude of a damped oscillator decreases to 0.9 times its original magnitude in 5s. In another 10s it will decrease to \[\alpha \] times its original magnitude, where \[\alpha \] equals:                                            [JEE MAIN 2013]
  A)
   0.7                  
  done clear
  B)
        0.81
  done clear
  C)
  0.729           
  done clear
  D)
        0.6
  done clear
  View Answer play_arrow

• question_answer29) An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is \[{{V}_{0}}\] and its pressure is\[{{P}_{0}}\]. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency:     [JEE MAIN 2013]
  A)
   \[\frac{1}{2\pi }\frac{{{A}_{\gamma }}{{P}_{0}}}{{{V}_{0}}M}\]      
  done clear
  B)
        \[\frac{1}{2\pi }\frac{{{V}_{0}}M{{P}_{0}}}{{{A}^{2}}\gamma }\]
  done clear
  C)
   \[\frac{1}{2\pi }\sqrt{\frac{{{A}^{2}}\gamma {{P}_{0}}}{M{{V}_{0}}}}\]
  done clear
  D)
        \[\frac{1}{2\pi }\sqrt{\frac{M{{V}_{0}}}{{{A}_{\gamma }}{{P}_{0}}}}\]
  done clear
  View Answer play_arrow

• question_answer30) Two simple pendulums of length 1m and 4mrespectively are both given small d is placement in the same direction at the same instant. They will be again in phase after the shorter pendulum has completed number of oscillations equal to: [JEE ONLINE 09-04-2013]
  A)
         2        
  done clear
  B)
        7
  done clear
  C)
   5                    
  done clear
  D)
        3
  done clear
  View Answer play_arrow

• question_answer31) Bob of a simple pendulum of length \[l\] is mode of iron. The pendulum is oscillating over a horizontal coil carrying direct current. If the time period of the pendulum is T then: [JEE ONLINE 23-04-2013]
  A)
         \[T=2\pi \sqrt{\frac{l}{g}}\] and damping is smaller than in air alone.
  done clear
  B)
        \[T=2\pi \sqrt{\frac{l}{g}}\] and damping is larger than in air alone.
  done clear
  C)
        \[T>2\pi \sqrt{\frac{l}{g}}\] and damping is smaller than in air alone.
  done clear
  D)
        \[T<2\pi \sqrt{\frac{l}{g}}\] and damping is larger than in air alone.
  done clear
  View Answer play_arrow

• question_answer32) If the time period \[t\] of the oscillation of a drop of liquid of density \[d\]radius \[r,\]vibrating under surface tension s is given by the formula \[t=\sqrt{{{r}^{2b}}{{s}^{c}}{{d}^{a/2}}.}\] It is observe that the time period is directly proportional to \[\sqrt{\frac{d}{s}.}\] The value of \[b\] should therefore be:                         [JEE ONLINE 23-04-2013]
  A)
         \[\frac{3}{4}\]             
  done clear
  B)
        \[\sqrt{3}\]
  done clear
  C)
   \[\frac{3}{2}\] 
  done clear
  D)
        \[\frac{2}{3}\]
  done clear
  View Answer play_arrow

• question_answer33) A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, form a fixed point by a mass less  spring, such that it is half submerged in a liquid of density \[\sigma \] at equilibrium position. When the cylinder is given a downward push and released, it stats oscillating vertically with a small amplitude. The time period T of the oscillations of the cylinder will be:                                                                  [JEE ONLINE 25-04-2013]
  A)
         Smaller than \[2\pi \] \[{{\left[ \frac{\operatorname{M}}{\operatorname{k}+\operatorname{A}\sigma g} \right]}^{1/2}}\]
  done clear
  B)
   \[2\pi \sqrt{\frac{\operatorname{M}}{\operatorname{k}}}\]
  done clear
  C)
   Larger than \[2\pi {{\left[ \frac{\operatorname{M}}{(\operatorname{k}+\operatorname{A}\sigma g)} \right]}^{1/2}}\]
  done clear
  D)
        \[2\pi {{\left[ \frac{\operatorname{M}}{(\operatorname{k}+\operatorname{A}\sigma g)} \right]}^{1/2}}\] 
  done clear
  View Answer play_arrow

• question_answer34) A particle moves with simple harmonic motion in a straight line. In first \[\tau s\], after starting from rest it travels a distance a, and in next \[\tau s\] it travels 2a, in same direction, then:  [JEE MAIN 2014]
  A)
   amplitude of motion is 4a
  done clear
  B)
   time period of oscillations is \[6\tau \]
  done clear
  C)
   amplitude of motion is 3a
  done clear
  D)
   time period of oscillations is \[8\tau \]
  done clear
  View Answer play_arrow

• question_answer35) A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is 340 m/s.                             [JEE MAIN 2014]
  A)
   6                    
  done clear
  B)
        4
  done clear
  C)
   12                   
  done clear
  D)
        8
  done clear
  View Answer play_arrow

• question_answer36) An experiment is performed to obtain the value of acceleration due to gravity g by using a simple pendulum of length L. In this experiment time for 100 oscillations is measured by using a watch of 1 second least count and the value is 90.0 seconds. The length L is measured by using a meter scale of least count 1 mm and the value is 20.0 cm. The error in the determination of g would be:            [JEE ONLINE 09-04-2014]
  A)
   1.7%   
  done clear
  B)
        2.7%
  done clear
  C)
   4.4%   
  done clear
  D)
        2.27%
  done clear
  View Answer play_arrow

• question_answer37) 

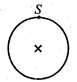  Two bodies of masses 1 kg and 4 kg are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency 25rad/s, and amplitude 1.6 cm while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \[g=10m{{s}^{-2}}\])     [JEE ONLINE 09-04-2014]

  A)
   20 N   
  done clear
  B)
        10 N
  done clear
  C)
   60 N   
  done clear
  D)
        40 N
  done clear
  View Answer play_arrow

• question_answer38) The amplitude of a simple pendulum, oscillating in air with as mall spherical bob, decreases from 10 cm to 8 cm in 40seconds. Assuming that Stokes law is valid, and ratio of the coefficient of viscosity of air to that of carbon dioxide is 1.3. The time in which amplitude of this pendulum will reduce from 10 cm to 5 cm in carbon dioxide will be close to (In 5 =1.601, In 2 = 0.693).                                                                           [JEE ONLINE 09-04-2014]
  A)
   231 s   
  done clear
  B)
        208 s
  done clear
  C)
   161 s   
  done clear
  D)
        142 s
  done clear
  View Answer play_arrow

• question_answer39) A particle which is simultaneously subjected to two perpendicular simple harmonic motions represented by\[;x={{a}_{1}}\cos \omega t\]and\[y={{a}_{2}}\cos 2\omega t\]traces a curve given by: [JEE ONLINE 09-04-2014]
  A)
           
  done clear
  B)
   
  done clear
  C)
   
  done clear
  D)
        
  done clear
  View Answer play_arrow

• question_answer40) The angular frequency of the damped oscillator is given by,\[\omega =\sqrt{\left( \frac{k}{m}-\frac{{{r}^{2}}}{4{{m}^{2}}} \right)}\]where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio\[\frac{{{r}^{2}}}{mk}\]is 8%, the change in time period compared to the undamped oscillator is approximately as follows: [JEE ONLINE 11-04-2014]
  A)
   increases by 1%
  done clear
  B)
        increases by 8%
  done clear
  C)
   decreases by 1%
  done clear
  D)
        decreases by 8%
  done clear
  View Answer play_arrow

• question_answer41) Which of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a, b, c are positive constants?                                                       [JEE ONLINE 12-04-2014]
  A)
   \[a+bx-c{{x}^{2}}\]  
  done clear
  B)
        \[b{{x}^{2}}\]
  done clear
  C)
   \[a-bx+c{{x}^{2}}\]  
  done clear
  D)
        \[-bx\]
  done clear
  View Answer play_arrow

• question_answer42) A body is in simple harmonic motion with time period half second (T = 0.5 s) and amplitude one cm (A = 1 cm). Find the average velocity in the interval in which it moves form equilibrium position to half of its amplitude.              [JEE ONLINE 19-04-2014]
  A)
   4 cm/s
  done clear
  B)
        6 cm/s
  done clear
  C)
   12 cm/s
  done clear
  D)
       16 cm/s
  done clear
  View Answer play_arrow

• question_answer43) A pendulum made of a uniform wire of cross sectional area A has time period T. When an additional mass M is added to its bob, the time period change to \[{{T}_{M}}.\]If the Young’s modulus of the material of the wire is Y then\[\frac{1}{Y}\]is equal to: [JEE MAIN 2015] (g = gravitational acceleration)
  A)
   \[\left[ 1-{{\left( \frac{{{T}_{M}}}{T} \right)}^{2}} \right]\frac{A}{Mg}\]
  done clear
  B)
   \[\left[ 1-{{\left( \frac{T}{{{T}_{M}}} \right)}^{2}} \right]\frac{A}{Mg}\]
  done clear
  C)
   \[\left[ {{\left( \frac{{{T}_{M}}}{T} \right)}^{2}}-1 \right]\frac{A}{Mg}\]
  done clear
  D)
        \[\left[ {{\left( \frac{{{T}_{M}}}{T} \right)}^{2}}-1 \right]\frac{Mg}{A}\]
  done clear
  View Answer play_arrow

• question_answer44) For a simple pendulum, a graph is plotted between its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?                                       [JEE MAIN 2015] (graph are schematic and not drawn to scale)
  A)
   
  done clear
  B)
        
  done clear
  C)
         
  done clear
  D)
  

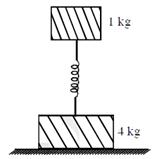  done clear View Answer play_arrow question_answer45) The period of oscillation of a simple pendulum is \[T=2\pi \sqrt{\frac{L}{g}}.\]Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1s resolution. The accuracy in the determination of g is: [JEE MAIN 2015] A)  1%       done clear B)                   5% done clear C)  2%                   done clear D)       3% done clear View Answer play_arrow question_answer46) A simple harmonic oscillator of angular frequency \[2rad\,{{s}^{-1}}\]is acted upon by an external force \[F=\sin \,t\,N\]. If the oscillator is at rest in its equilibrium position at t = 0, its position at later times is proportional to: [JEE ONLINE 10-04-2015] A) \[\sin t+\frac{1}{2}\cos 2t\] done clear B)      \[\sin t-\frac{1}{2}\sin 2t\] done clear C) \[\cot t-\frac{1}{2}\sin 2t\] done clear D)      \[\sin t+\frac{1}{2}\sin 2t\] done clear View Answer play_arrow question_answer47) x and y displacements of a particle are given as x(t)=a \[\sin \omega t\] and \[y(t)=a\sin 2\omega t.\] Its trajectory will look like:                                                                        [JEE ONLINE 10-04-2015] A)   done clear 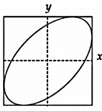B)        done 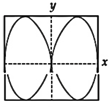clear C)   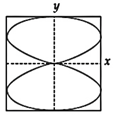done clear D)      done clear View Answer play_arrow 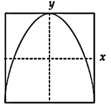question_answer48) A cylindrical block of wood (density \[=650\,kg\,{{m}^{-3}}\]), of base area \[30\text{ }c{{m}^{2}}\]and height 54 cm, floats in a liquid of density \[900\text{ }kg{{m}^{-}}^{3}.\]The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly):                          [JEE MAIN 11-04-2015] A)  65 cm  done clear B)       52 cm done clear C)  39 cm  done clear D)       26 cm done clear View Answer play_arrow question_answer49) A pendulum with time period of 1s is losing energy due to damping. At certain time its energy is 45 J. If after completing 15 oscillations, its energy has become 15 J, its damping constant (in\[{{s}^{-1}}\]) is:   [JEE MAIN 11-04-2015] A) \[\frac{1}{30}\ln 3\]       done clear B)      \[\frac{1}{15}\ln 3\] done clear C)  2                     done clear D)      \[\frac{1}{2}\] done clear View Answer play_arrow question_answer50) A particle performs simple harmonic motion with amplitude A. Its speed is trebled at the instant that it is at a distance\[\frac{2A}{3}\]from equilibrium position.                          [JEE MAIN - I 3-4-2016] The new amplitude of the motion is:- A) \[\frac{7A}{3}\] done clear B)      \[\frac{A}{3}\sqrt{41}\] done clear C)  3A                   done clear D)       A 3 done clear View Answer play_arrow question_answer51)  Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to A and T, respectively. At time t = 0 one particle has displacement A while the other one has displacement \[\frac{-A}{2}\]and they are moving towards each other .If they cross each at time t, then t is:                                                                          [JEE ONLINE 09-04-2016] A) \[\frac{T}{4}\]               done clear B)      \[\frac{5T}{6}\] done clear C) \[\frac{T}{3}\]               done clear D)      \[\frac{T}{6}\] done clear View Answer play_arrow question_answer52) In an engine the piston undergoes vertical simple harmonic motion with amplitude 7cm. A washer rests on top of the piston and moves with it. The motor speed is slowly increased. 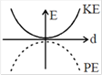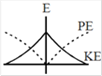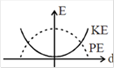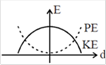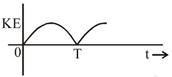The frequency of the piston at which the washer longer stays in contact with the piston, is closed to:                                                                [JEE ONLINE 10-04-2016] A)  0.7 Hz done clear B)       1.2 Hz done clear C)  1.9 Hz done clear D)       0.1 Hz done clear View Answer play_arrow question_answer53) A particle is executing simple harmonic motion with a time period T. AT time t = 0, it is at its position of equilibrium. 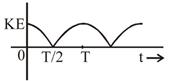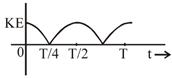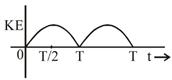The kinetic energy-time graph of the particle will look like                                              [JEE Main 2017] A)   done clear B)   done clear C)   done clear D)   done clear View Answer play_arrow question_answer54) A 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is                                                                                  [JEE Online 08-04-2017] A)  2 Hz     done clear B)      \[\frac{1}{4}Hz\] done clear C) \[\frac{1}{2\sqrt{2}}Hz\] done clear D)      \[\frac{1}{2}Hz\] done clear View Answer play_arrow question_answer55)  The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is \[10{{s}^{-1}}.\]     At, t = 0 the displacement is 5 m. What is the maximum acceleration? The initial phase is\[\frac{\pi }{4}.\]      [JEE Online 08-04-2017] A) \[500m/{{s}^{2}}\] done clear B)                  \[750\sqrt{2}m/{{s}^{2}}\] done clear C) \[750m/{{s}^{2}}\]      done clear D)      \[500\sqrt{2}m/{{s}^{2}}\] done clear View Answer play_arrow question_answer56) A block of mass 0.1 kg is connected to an elastic spring of spring constant \[640\,\,N{{m}^{-1}}\] and oscillates in a damping medium of damping constant \[{{10}^{-2}}kg\,{{s}^{-1}}\]. The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to [JEE Online 09-04-2017] A)  2 s                   done clear B)       5 s done clear C)  7 s                   done clear D)       3.5 s done clear View Answer play_arrow question_answer57) In an experiment to determine the period of a simple pendulum of length 1m, it is attached to different spherical bobs of radii \[{{r}_{1}}\] and \[{{r}_{2}}\]. The two spherical bobs have uniform mass distribution. If the relative difference in the periods, is found to be \[5\times {{10}^{-4}}s,\] the difference in radii, \[|{{r}_{1}}-{{r}_{2}}|\] is best given by –                                       [JEE Online 09-04-2017] A)  0.01 cm            done clear B)      (2) 0.1 cm done clear C)  0.5 cm done clear D)       1 cm done clear View Answer play_arrow question_answer58) A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of \[{{10}^{12}}/\sec \]. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avagadro number\[\text{=6}\text{.02}\times \text{1}{{\text{0}}^{\text{23}}}\text{ gm mol}{{\text{e}}^{\text{-1}}}\]).                                                                                         [JEE Main Online 08-04-2018] A)  \[2.2\,\,N/m\]                 done clear B)  \[5.5\,\,N/m\] done clear C)  \[6.4\,\,N/m\]     done clear D)       \[7.1\,\,N/m\] done clear View Answer play_arrow question_answer59)  Two simple harmonic motions, as shown, are at right angles. They are combined to form Lissajous figures. \[x(t)=A\sin (at+\delta )\] \[y(t)=B\sin (bt)\] Identify the correct match below                                                                           [JEE Online 15-04-2018 (II)] A)  \[\text{Parameters: A=B, a=2b;}\delta \text{=}\frac{\pi }{2};Curve:Circle\] done clear B)  \[\text{Parameters: A=B, a=b;}\delta \text{=}\frac{\pi }{2};Curve:line\] done clear C)  \[\text{Parameters: A}\ne \text{B, a=b; }\delta \text{=}\frac{\pi }{2};Curve:\text{Ellipse}\] done clear D)  \[\text{Parameters:}A\ne B,a=b;\delta =0;\text{Curve : Parabola}\] done clear View Answer play_arrow question_answer60) An oscillator of mass M is at rest in its equilibrium position in a potential \[V=\frac{1}{2}k{{(x-X)}^{2}}.\]A particle of mass comes from right with speed u and collides completely in elastically with and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after collisions is:\[(M=10,m=5,u=1,k=1).\] [JEE Main Online 16-4-2018] A) \[\frac{1}{2}\]                           done clear B)  \[\frac{1}{\sqrt{3}}\] done clear C)  \[\frac{2}{3}\]              done clear D)      \[\sqrt{\frac{3}{5}}\] done clear View Answer play_arrow question_answer61) A rod of mass ‘M’ and length ‘2L’ is suspended at its middle by a wire. It exhibits torsional oscillations; If two masses each of ‘m’ are attached at distance ‘L/2’ from its centre on both sides, it reduces the oscillation frequency by \[20%\]. The value of ratio m/M is close to:                                                              [JEE Main 09-Jan-2019 Evening] A) 0.37            done clear B)       0.57 done clear C)  0.77                 done clear D)       0.17 done clear View Answer play_arrow question_answer62) A particle is executing simple harmonic motion (SHM) of amplitude A, along the x-axis, about\[x=0\]. When its potential Energy (PE) equals kinetic energy (KE), the position of the particle will be:      [JEE Main 09-Jan-2019 Evening] A)  \[\frac{A}{2\sqrt{2}}\]               done clear B)       \[\frac{A}{\sqrt{2}}\] done clear C)  \[\frac{A}{2}\]              done clear D)       A done clear View Answer play_arrow question_answer63) A cylindrical plastic bottle of negligible mass is filled with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency co. If the radius of the bottle is 2.5 cm then co is close to - (density of water\[={{10}^{3}}kg/{{m}^{3}}\]).      [JEE Main 10-Jan-2019 Evening] A)  \[2.50\text{ }rad\text{ }{{s}^{-}}^{1}\]          done clear B)       \[3.75\text{ }rad\text{ }{{s}^{-1}}\] done clear C)  \[5.00\text{ }rad\text{ }{{s}^{-1}}\]     done clear D)      None of these done clear View Answer play_arrow question_answer64) A particle executes simple harmonic motion with an amplitude of 5 cm. When the particle is at 4 cm from the mean position, the magnitude of its velocity in SI units is equal to that of its acceleration. Then, its periodic time in seconds is-            [JEE Main 10-Jan-2019 Evening] A)  \[\frac{4\pi }{3}\]          done clear B)       \[\frac{3\,}{8}\pi \] done clear C)  \[\frac{7\,}{3}\pi \]                    done clear D)       \[\frac{8\,\pi }{3}\] done clear View Answer play_arrow question_answer65) A particle undergoing simple harmonic motion has time dependent displacement given by \[x(t)=A\sin \frac{\pi t}{90}.\] The ratio of kinetic to potential energy of this particle at t = 210 s will be- [JEE Main 11-Jan-2019 Morning] A)  \[\frac{1}{9}\]              done clear B)       2      done clear C)  1                     done clear D)      None of these done clear View Answer play_arrow question_answer66) A pendulum is executing simple harmonic motion and its maximum kinetic energy is \[{{K}_{1}}\]. If the length of the pendulum is doubled and it performs simple harmonic motion with the same amplitude as in the first case. its maximum kinetic energy is \[{{K}_{2}}\]. Then                                                       [JEE Main 11-Jan-2019 Evening] A) \[{{K}_{2}}={{K}_{1}}\]         done clear B)                  \[{{K}_{2}}=\frac{{{K}_{1}}}{2}\] done clear C) \[{{K}_{2}}=2{{K}_{1}}\]        done clear D)                  \[{{K}_{2}}=\frac{{{K}_{1}}}{4}\] done clear View Answer play_arrow question_answer67) The mass and the diameter of a planet are three times the respective values for the Earth. The period of oscillation of a simple pendulum on the Earth is 2 s. The period of oscillation of the same pendulum on the planet would be- [JEE Main 11-Jan-2019 Evening] A) \[2\sqrt{3}s\]      done clear B)      \[\frac{3}{2}s\] done clear C) \[\frac{2}{\sqrt{3}}s\]     done clear D)                  \[\frac{\sqrt{3}}{2}s\] done clear View Answer play_arrow question_answer68) A simple pendulum of length 1 m is oscillating with an angular frequency 10 rad/s. The support of the pendulum starts oscillating up and down with a small angular frequency of 1 rad/s and an amplitude of \[{{10}^{-2}}\]m. The relative change in the angular frequency of the pendulum is best given by-    [JEE Main 11-Jan-2019 Evening] A) \[{{10}^{-5}}rad/s\]     done clear B)      \[{{10}^{-1}}rad/s\] done clear C) \[1rad/s\]            done clear D)      \[{{10}^{-3}}rad/s\] done clear View Answer play_arrow question_answer69) A simple pendulum, made of a string of length I and a bob of mass m, is released from a small angle \[{{\theta }_{0}}.\]It strikes a block of mass M, kept on a horizontal surface at its lowest point of oscillations, elastically. It bounces back and goes up to an angle \[{{\theta}_{1}}.\]Then M is given by-                                 [JEE Main 12-Jan-2019 Morning] A) \[\frac{m}{2}\left( \frac{{{\theta }_{0}}-{{\theta }_{1}}}{{{\theta }_{0}}+{{\theta }_{1}}} \right)\]         done clear B)      \[m\left( \frac{{{\theta }_{0}}+{{\theta }_{1}}}{{{\theta }_{0}}-{{\theta }_{1}}} \right)\] done clear C) \[\frac{m}{2}\left( \frac{{{\theta }_{0}}+{{\theta }_{1}}}{{{\theta }_{0}}-{{\theta }_{1}}} \right)\]         done clear D)      \[m\left( \frac{{{\theta }_{0}}-{{\theta }_{1}}}{{{\theta }_{0}}+{{\theta }_{1}}} \right)\] done clear View Answer play_arrow question_answer70)  A simple harmonic motion is represented by                                               [JEE Main 12-Jan-2019 Evening] \[y=5(sin3\pi t+\sqrt{3}cos3\pi t)cm\] The amplitude and time period of the motion are A) \[5cm,\frac{3}{2}s\]       done clear B)      \[10cm,\frac{2}{3}s\] done clear C) \[5cm,\frac{2}{3}s\]       done clear D)      \[10cm,\frac{3}{2}s\] done clear View Answer play_arrow question_answer71) A damped harmonic oscillator has a frequency of 5 oscillations per second. The amplitude drops to half its value for every 10 oscillations. The time it will take to drop to \[\frac{1}{1000}\]of the original amplitude is close to: [JEE Main 8-4-2019 Afternoon] A)  100 s    done clear B)       20 s done clear C)  10 s                 done clear D)       50 s done clear View Answer play_arrow question_answer72) In a simple pendulum experiment for determination of acceleration due to gravity (g), time taken for 20 oscillations is measured by using a watch of 1 second least count. The mean value of time taken comes out to be 30 s. The length of pendulum is measured by using a meter scale of least count 1 mm and the value obtained is 55.0 cm. The percentage error in the determination of g is close to:-                                                  [JEE Main 8-4-2019 Afternoon] A)  0.7%    done clear B)       0.2% done clear C)  3.5%    done clear D)       6.8% done clear View Answer play_arrow question_answer73) A simple pendulum oscillating in air has period T. The bob of the pendulum is completely immersed in a non-viscous liquid. The density of the liquid is \[\frac{1}{16}\]th of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is :                                                              [JEE Main 9-4-2019 Morning] A) \[4T\sqrt{\frac{1}{15}}\] done clear B)      \[2T\sqrt{\frac{1}{10}}\] done clear C) \[4T\sqrt{\frac{1}{14}}\] done clear D)      \[2T\sqrt{\frac{1}{14}}\] done clear View Answer play_arrow question_answer74) A string 2.0 m long and fixed at its ends is driven by a 240 Hz vibrator. The string vibrates in its third harmonic mode. The speed of the wave and its fundamental frequency is :-                               [JEE Main 9-4-2019 Afternoon] A)  320m/s, 120 Hz done clear B)       180m/s, 80 Hz done clear C)  180m/s, 120 Hz done clear D)       320m/s, 80 Hz done clear View Answer play_arrow question_answer75) The displacement of a damped harmonic oscillator is given by \[x(t)={{e}^{-01.1t}}\cos (10\pi t+\phi ).\]Here t is in seconds. The time taken for its amplitude of vibration to drop to half of its initial value is close to:          [JEE Main 10-4-2019 Morning] A)  13 s                 done clear B)       7 s done clear C)  27 s                 done clear D)       4 s done clear View Answer play_arrow question_answer76) A simple pendulum is being used to determine the value of gravitational acceleration g at a certain place. The length of the pendulum is 25.0 cm and a stopwatch with 1 s resolution measures the time taken for 40 oscillation to be 50 s. The accuracy in g is [JEE MAIN Held on 08-01-2020 Evening] A)  3.40%  done clear B)       2.40% done clear C)  5.40%  done clear D)       4.40% done clear View Answer play_arrow Study Package JEE PYQ-Simple Harmonic Motion   Buy Now     Please Wait you are being redirected.... You need to login to perform this action. You will be redirected in 3 sec × Reset Password. Email : Send Password Cancel Add Mobile Enter Mobile Number Submit Logout Enter OTP OTP has been sent to your mobile number and is valid for one hour Enter One Time Password Submit Change Mobile: Submit Logout Mobile Number Verified Your mobile number is verified. Close Free Videos × For free video lectures fill in the form below and we will get back to you. * Email Address: * Mobile Number: Submit Cancel