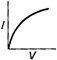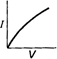question_answer 1) Which of the following rays can be polarised?
A)
Water wave and sound wave
done
clear
B)
Sound wave and radio wave
done
clear
C)
\[X-\]rays and water wave
done
clear
D)
Light wave and \[X-\] ray
done
clear
View Answer play_arrow
question_answer 2) Quantum nature can prove :
A)
interference
done
clear
B)
photoelectric effect
done
clear
C)
diffraction
done
clear
D)
polarisation
done
clear
View Answer play_arrow
question_answer 3) Which one has highest binding energy per nucleon?
A)
\[F{{e}^{56}}\]
done
clear
B)
\[L{{i}^{6}}\]
done
clear
C)
\[{{U}^{235}}\]
done
clear
D)
\[C{{a}^{40}}\]
done
clear
View Answer play_arrow
question_answer 4) Huygen's wave theory can't explain:
A)
interference
done
clear
B)
photoelectric effect
done
clear
C)
diffraction
done
clear
D)
all of these
done
clear
View Answer play_arrow
question_answer 5) If the refractive index of a glass prism is \[\cot (A/2)\] and \[A\] is angle of prism, then angle of minimum deviation is:
A)
\[\left( \frac{\pi }{2}-A \right)\]
done
clear
B)
\[\left( 2\pi -\frac{A}{2} \right)\]
done
clear
C)
\[\left( \frac{\pi -A}{2} \right)\]
done
clear
D)
\[(\pi -2A)\]
done
clear
View Answer play_arrow
question_answer 6)
If \[f\] is the frequency when mass m is attached to a spring of spring constant \[k\], then new frequency for this arrangement, is:
A)
\[f/2\]
done
clear
B)
\[\sqrt{2f}\]
done
clear
C)
\[f/\sqrt{2}\]
done
clear
D)
\[2\sqrt{2f}\]
done
clear
View Answer play_arrow
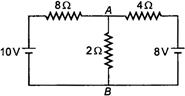
question_answer 7)
What is equivalent capacitance of the network? Each capacitor has \[1\mu F\] capacitance:
A)
\[\frac{1}{3}\mu F\]
done
clear
B)
\[2\mu F\]
done
clear
C)
\[\frac{3}{2}\mu F\]
done
clear
D)
\[3\mu F\]
done
clear
View Answer play_arrow
question_answer 8) The two capacitors \[{{C}_{1}}\]and\[{{C}_{2}}\]are charged to potentials \[{{V}_{1}}\] and \[{{V}_{2}}\] then connected in parallel. There will be no flow of energy, if:
A)
\[{{C}_{1}}{{V}_{1}}={{C}_{2}}{{V}_{2}}\]
done
clear
B)
\[{{V}_{1}}={{V}_{2}}\]
done
clear
C)
\[{{C}_{1}}={{C}_{2}}\]
done
clear
D)
\[\frac{{{C}_{1}}}{{{V}_{1}}}=\frac{{{C}_{2}}}{{{V}_{2}}}\]
done
clear
View Answer play_arrow
question_answer 9) Which is not the unit of electric field?
A)
\[\frac{N}{C}\]
done
clear
B)
\[\frac{N-m}{C}\]
done
clear
C)
\[\frac{V}{m}\]
done
clear
D)
\[\frac{J}{C\text{-}m}\]
done
clear
View Answer play_arrow
question_answer 10) If a body moves for \[2\,\,s\] with \[15\,\,m/s\] velocity towards east and then moves with \[5\,\,m/s\] velocity for \[8\,\,s\] towards north, then average velocity is:
A)
\[5\,\,m/s\]
done
clear
B)
\[15\,\,m/s\]
done
clear
C)
\[30\,\,m/s\]
done
clear
D)
\[7.5\,\,m/s\]
done
clear
View Answer play_arrow
question_answer 11) For monoatomic gas which is correct?
A)
\[CV=\frac{3}{5}R\]
done
clear
B)
\[{{C}_{P}}=\frac{5}{2}R\]
done
clear
C)
\[{{C}_{P}}-{{C}_{V}}=2R\]
done
clear
D)
\[\frac{{{C}_{P}}}{{{C}_{V}}}=\frac{3}{5}\]
done
clear
View Answer play_arrow
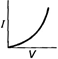
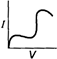
question_answer 12) Which is correct relationship for diode?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 13) In a properly biased transistor:
A)
both depletion layers are equally large
done
clear
B)
both depletion layers are equally small
done
clear
C)
emitter-base depletion layer is large but base-collector depletion layer is small
done
clear
D)
emitter-base depletion layer is small but base-collector depletion layer is large
done
clear
View Answer play_arrow
question_answer 14) A wire has resistance \[20\,\,\Omega \]. If its length is increased three times its initial length, then new resistance is:
A)
\[40\Omega \]
done
clear
B)
\[80\Omega \]
done
clear
C)
\[60\Omega \]
done
clear
D)
\[180\Omega \]
done
clear
View Answer play_arrow
question_answer 15) A circular coil of diameter \[d\] is rotated in electric field such that electric flux is changed from zero to maximum value \[\phi \] then, electric field is:
A)
\[\frac{\phi }{\pi {{d}^{2}}}\]
done
clear
B)
\[\frac{2\phi }{\pi {{d}^{2}}}\]
done
clear
C)
\[\frac{4{{d}^{2}}}{\pi {{\phi }^{2}}}\]
done
clear
D)
\[\frac{4\phi }{\pi {{d}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 16) Work done in rotating a bar magnet from \[0\] to angle \[\theta \] is:
A)
\[MH(1-\cos \theta )\]
done
clear
B)
\[\frac{M}{H}(1-\cos \theta )\]
done
clear
C)
\[\frac{M}{H}(\cos \theta -1)\]
done
clear
D)
\[MH(\cos \theta -1)\]
done
clear
View Answer play_arrow
question_answer 17) If a convex lens of refractive index \[1.44\] is dipped in liquid of refractive index \[1.49\], then it behaves as:
A)
concave lens
done
clear
B)
convex lens
done
clear
C)
mirror
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 18) If a source approaches and recedes from observer with same velocity, the ratio of frequencies (apparent) is \[6:5\], then velocity of source is:\[({{v}_{s}}=330\,\,m/s)\]
A)
\[20\,\,m/s\]
done
clear
B)
\[10\,\,m/s\]
done
clear
C)
\[30\,\,m/s\]
done
clear
D)
\[33\,\,m/s\]
done
clear
View Answer play_arrow
question_answer 19) If a boy swings in a circle so the minimum and maximum height from ground is\[3\,\,m\]and\[6\,\,m\], then, its maximum velocity is:
A)
\[5\sqrt{2}m/s\]
done
clear
B)
\[2\sqrt{5}m/s\]
done
clear
C)
\[3\sqrt{5}m/s\]
done
clear
D)
\[5\sqrt{3}m/s\]
done
clear
View Answer play_arrow
question_answer 20) If percentage decrease in radius of earth is \[1%\] without changing its mass, then percentage change in acceleration due to gravity is:
A)
\[2%\] decrease
done
clear
B)
\[2%\] increase
done
clear
C)
\[1%\] decrease
done
clear
D)
\[1%\] increase
done
clear
View Answer play_arrow
question_answer 21) A black body radiates at two temperatures \[{{T}_{1}}\] and \[{{T}_{2}}\] such that\[{{T}_{1}}<{{T}_{2}}\]. The frequency corresponding to maximum intensity is:
A)
less at\[{{T}_{1}}\]
done
clear
B)
more at\[{{T}_{1}}\]
done
clear
C)
equally in the two cases
done
clear
D)
cannot say
done
clear
View Answer play_arrow
question_answer 22) If temperature is increased by \[1\,\,K\] at constant volume, then work done on the gas is:
A)
\[\frac{5}{2}R\]
done
clear
B)
\[\frac{3}{2}R\]
done
clear
C)
\[zero\]
done
clear
D)
\[\frac{1}{2}R\]
done
clear
View Answer play_arrow
question_answer 23) A body cools from\[{{75}^{o}}C\] to\[{{70}^{o}}C\] in time \[{{t}_{1}}\], from \[{{70}^{o}}C\] to \[{{65}^{o}}C\] in time \[{{t}_{2}}\] and from \[{{65}^{o}}C\] to \[{{60}^{o}}C\] in timer\[3\], then:
A)
\[{{t}_{3}}>{{t}_{2}}>{{t}_{1}}\]
done
clear
B)
\[{{t}_{1}}>{{t}_{2}}>{{t}_{3}}\]
done
clear
C)
\[{{t}_{2}}>{{t}_{1}}={{t}_{3}}\]
done
clear
D)
\[{{t}_{1}}>{{t}_{2}}>{{t}_{3}}\]
done
clear
View Answer play_arrow
question_answer 24) A gas is at \[{{27}^{o}}C\]. Its volume is doubled keeping pressure constant, then final temperature is:
A)
\[{{600}^{o}}C\]
done
clear
B)
\[327\,\,K\]
done
clear
C)
\[{{327}^{o}}C\]
done
clear
D)
\[{{273}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 25) If the volume of gas is changed from \[{{V}_{1}}\] to \[{{V}_{2}}\] isothermally, then work done is:
A)
\[RT\ln \frac{{{V}_{1}}}{{{V}_{2}}}\]
done
clear
B)
\[RT\ln \frac{{{V}_{2}}}{{{V}_{1}}}\]
done
clear
C)
\[R({{T}_{2}}-{{T}_{1}})\ln \frac{{{V}_{2}}}{{{V}_{1}}}\]
done
clear
D)
\[R({{V}_{2}}-{{V}_{1}})\ln \frac{{{T}_{2}}}{{{T}_{1}}}\]
done
clear
View Answer play_arrow
question_answer 26) If energy is supplied to a gas is ochorically, increase in internal energy is \[dU\] then:
A)
\[dQ=dU+dW\]
done
clear
B)
\[dQ=dU-dW\]
done
clear
C)
\[dQ=dU\]
done
clear
D)
\[dQ=-dU\]
done
clear
View Answer play_arrow
question_answer 27) A nucleus \[_{Z}^{A}X\] emits one a and \[2\beta \] particles, then final nucleus is:
A)
\[Y_{Z-2}^{A}\]
done
clear
B)
\[Y_{Z-4}^{A-4}\]
done
clear
C)
\[Y_{Z}^{A-4}\]
done
clear
D)
\[X_{Z}^{A}\]
done
clear
View Answer play_arrow
question_answer 28) The fringe width for red light is approximately how many times that for violet light in Young's slit experiment?
A)
\[2\] times
done
clear
B)
\[3\] times
done
clear
C)
Equal
done
clear
D)
\[1/2\] times
done
clear
View Answer play_arrow
question_answer 29) A person sees clearly at a distance of \[100\,\,cm\], then power of lens used to see object at \[40\,\,cm\] is:
A)
\[3D\]
done
clear
B)
\[-3D\]
done
clear
C)
\[-1.5D\]
done
clear
D)
\[+1.5D\]
done
clear
View Answer play_arrow
question_answer 30) The electric potential \[V\] is given as a function of distance \[x\] (metre) by\[V=(5{{x}^{2}}+10x-4)V\]. Value of electric field at \[x=1\,\,m\] is:
A)
\[-23\,\,V/m\]
done
clear
B)
\[11\,\,V/m\]
done
clear
C)
\[6\,\,V/m\]
done
clear
D)
\[-20\,\,V/m\]
done
clear
View Answer play_arrow
question_answer 31) In an image converter tube fluorescent material is bombarded by:
A)
visible radiation
done
clear
B)
electron radiation
done
clear
C)
infrared radiation
done
clear
D)
ultra violet radiation
done
clear
View Answer play_arrow
question_answer 32) A particle executes simple harmonic motion with a frequency\[f\]. The frequency with which its kinetic energy oscillates is:
A)
\[f/2\]
done
clear
B)
\[f\]
done
clear
C)
\[2f\]
done
clear
D)
\[4f\]
done
clear
View Answer play_arrow
question_answer 33) The work done by the centripetal force \[F\] when the body completes one rotation around the circle of radius \[R\] is:
A)
\[2\pi RF\]
done
clear
B)
\[2RF\]
done
clear
C)
\[RF\]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 34) The unit mass having \[\overset{\to }{\mathop{\mathbf{r}}}\,=8\widehat{\mathbf{i}}-4\widehat{\mathbf{j}}\] and \[\overset{\to }{\mathop{\mathbf{v}}}\,=8\widehat{\mathbf{i}}+4\widehat{\mathbf{j}}\] in its angular momentum is:
A)
\[64\] unit in \[-\mathbf{\hat{k}}\] direction
done
clear
B)
\[64\]unit in \[+\mathbf{\hat{k}}\] direction
done
clear
C)
\[64\]unit in \[+\widehat{\mathbf{j}}\] direction
done
clear
D)
\[64\]unit in \[+\widehat{\mathbf{i}}\] direction
done
clear
View Answer play_arrow
question_answer 35) Which is nuclear fusion direction?
A)
Hydrogen to helium
done
clear
B)
Uranium to krypton
done
clear
C)
Hydrogen to water
done
clear
D)
Neutron to proton
done
clear
View Answer play_arrow
question_answer 36) If an \[AC\] produces same heat as that produced by a steady current of \[4\,\,A\], then peak value of current is:
A)
\[4\,\,A\]
done
clear
B)
\[1.56\,\,A\]
done
clear
C)
\[5.6\,\,A\]
done
clear
D)
\[1.41\,\,A\]
done
clear
View Answer play_arrow
question_answer 37) In\[LCR\]circuit \[f=\frac{50}{\pi }Hz,\] \[V=50\,\,volt,\]\[R=300\Omega \]. If\[L=1\,\,H\]and\[C=20\,\,\mu C\], then voltage across capacitor is:
A)
\[zero\]
done
clear
B)
\[20\,\,V\]
done
clear
C)
\[30\,\,V\]
done
clear
D)
\[50\,\,V\]
done
clear
View Answer play_arrow
question_answer 38) If two forces each of \[2\,\,N\] are inclined at \[{{60}^{o}}\], then resultant force is:
A)
\[2\,\,N\]
done
clear
B)
\[2\sqrt{5}N\]
done
clear
C)
\[3\sqrt{2}N\]
done
clear
D)
\[4\sqrt{2}N\]
done
clear
View Answer play_arrow
question_answer 39) A block of mass \[10\,\,kg\] is placed on a rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of \[100\,\,N\] is applied on it, then acceleration of block will be:
A)
\[10\,\,m/{{s}^{2}}\]
done
clear
B)
\[5\,\,m/{{s}^{2}}\]
done
clear
C)
\[15\,\,m/{{s}^{2}}\]
done
clear
D)
\[0.5\,\,m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 40) The potential difference across an instrument in a \[AC\] circuit of frequency \[f\] is \[V\] and the current through it is \[I\] such that \[V=5\cos 2\pi ft\,\,volt\] and \[I=2\sin 2\pi ft\,\,amp\]. The power dissipated in the instrument is:
A)
\[zero\]
done
clear
B)
\[10\,\,W\]
done
clear
C)
\[5\,\,W\]
done
clear
D)
\[2.5\,\,W\]
done
clear
View Answer play_arrow
question_answer 41) If ratio of intensities of interfering waves is \[16:9\], then ratio of maximum to minimum intensity is:
A)
\[49:1\]
done
clear
B)
\[225:81\]
done
clear
C)
\[3:1\]
done
clear
D)
\[9:1\]
done
clear
View Answer play_arrow
question_answer 42) The power of a lens, a short sighted person uses is \[-2\,\,D\]. Find the maximum distance of an object which he can see without spectacles:
A)
\[25\,\,cm\]
done
clear
B)
\[50\,\,cm\]
done
clear
C)
\[100\,\,cm\]
done
clear
D)
\[10\,\,cm\]
done
clear
View Answer play_arrow
question_answer 43) The first overtone frequency of a wave on string of length \[2\,\,m\] is \[250\,\,Hz\]. Then, its velocity is:
A)
\[1000\,\,m/s\]
done
clear
B)
\[25\,\,m/s\]
done
clear
C)
\[100\,\,cm\]
done
clear
D)
\[10\,\,cm\]
done
clear
View Answer play_arrow
question_answer 44)
What is the current flowing in arm\[AB\]?
A)
\[\frac{35}{4}A\]
done
clear
B)
\[\frac{13}{7}A\]
done
clear
C)
\[\frac{5}{7}A\]
done
clear
D)
\[\frac{7}{5}A\]
done
clear
View Answer play_arrow
question_answer 45) A projectile is fired making an angle \[2\theta \] with horizontal with velocity\[4\,\,m/s\]. At any instant it makes an angle \[\theta \], then its velocity is:
A)
\[4\cos \theta \]
done
clear
B)
\[4(2\cos \theta -\sec \theta )\]
done
clear
C)
\[2(\sec \theta +4\cos \theta )\]
done
clear
D)
\[4(\sec \theta +\cos \theta )\]
done
clear
View Answer play_arrow
question_answer 46) If path difference becomes \[(2n-1)\frac{\lambda }{2}\] then:
A)
white fringe is formed
done
clear
B)
bright fringe is formed
done
clear
C)
uniform illumination is obtained
done
clear
D)
dark fringe is formed
done
clear
View Answer play_arrow
question_answer 47) If the intensity of fringe at wavelength\[\lambda \]is\[K\], then its intensity at wavelength \[\lambda /2\] is:
A)
\[\frac{K}{2}\]
done
clear
B)
\[K\]
done
clear
C)
\[zero\]
done
clear
D)
\[\sqrt{2}K\]
done
clear
View Answer play_arrow
question_answer 48) A positively charged particle moving with velocity \[v\] enters a region of space having a uniform magnetic field \[B\]. The particle will experience the large deflecting force, when the angle between \[v\] and \[B\] is:
A)
\[{{0}^{o}}\]
done
clear
B)
\[{{45}^{o}}\]
done
clear
C)
\[{{90}^{o}}\]
done
clear
D)
\[{{180}^{o}}\]
done
clear
View Answer play_arrow
question_answer 49) In a step-up transformer the turn ratio is\[1:8\]. A lead accumulator \[(emf=6\,\,V)\] is connected across the primary coil of the transformer. The voltage across the secondary coil is:
A)
\[48\,\,V\]
done
clear
B)
\[0.75\,\,V\]
done
clear
C)
\[14\,\,V\]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 50) The mass of a lift is\[500\,\,kg\]. When it ascends with an acceleration of \[2m/{{s}^{2}}\] the tension in the cable will be:\[(g=10\,\,m/{{s}^{2}})\]
A)
\[6000\,\,N\]
done
clear
B)
\[5000\,\,N\]
done
clear
C)
\[4000\,\,N\]
done
clear
D)
\[1000\,\,N\]
done
clear
View Answer play_arrow
question_answer 51) A water molecule can form maximum number of \[H-\]bond which is equal to:
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 52) Bond angle in \[{{H}_{2}}O\] is:
A)
\[{{109}^{o}}28'\]
done
clear
B)
\[{{107}^{o}}10\]
done
clear
C)
\[{{104.5}^{o}}\]
done
clear
D)
\[{{92}^{o}}\]
done
clear
View Answer play_arrow
question_answer 53) Calamine is:
A)
\[ZnS\]
done
clear
B)
\[PbC{{O}_{3}}\]
done
clear
C)
\[ZnC{{O}_{3}}\]
done
clear
D)
\[MgC{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 54) Which is extremely stable?
A)
\[N{{F}_{3}}\]
done
clear
B)
\[NC{{l}_{3}}\]
done
clear
C)
\[NB{{r}_{3}}\]
done
clear
D)
\[N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 55) \[C{{H}_{3}}COCl\]does not react with:
A)
diethyl ether
done
clear
B)
phenol
done
clear
C)
ethanol
done
clear
D)
aniline
done
clear
View Answer play_arrow
question_answer 56) In \[S{{O}_{2}}\] hybridisation is:
A)
\[sp\]
done
clear
B)
\[s{{p}^{3}}\]
done
clear
C)
\[ds{{p}^{2}}\]
done
clear
D)
\[s{{p}^{2}}\]
done
clear
View Answer play_arrow
question_answer 57) Lowest melting point chloride is:
A)
\[LiCl\]
done
clear
B)
\[NaCl\]
done
clear
C)
\[KCl\]
done
clear
D)
\[CsCl\]
done
clear
View Answer play_arrow
question_answer 58) Half-life of a substance is\[6\min \]. If its initial amount is\[32\,\,g\], then amount present after \[18\,\,\min \] is:
A)
\[4\,\,g\]
done
clear
B)
\[8\,\,g\]
done
clear
C)
\[16\,\,g\]
done
clear
D)
\[2\,\,g\]
done
clear
View Answer play_arrow
question_answer 59) If calcium acetate and calcium for mate react, then product formed is:
A)
acetaldehyde
done
clear
B)
acetic acid
done
clear
C)
formic acid
done
clear
D)
ethyl for mate
done
clear
View Answer play_arrow
question_answer 60) Reduction with aluminium isopropoxide in excess of isopropyl alcohol is called Meer we in Pond or f Verley reduction\[(MPV)\]. What will be the firal product when cyclohex-2-enone is selectively reduced in \[MPV\] reaction?
A)
Cyclohexanol
done
clear
B)
Cyclohex-2-enol
done
clear
C)
Cyclohexanone
done
clear
D)
Benzene
done
clear
View Answer play_arrow
question_answer 61) If \[pH\] of a solution is\[4\], then \[{{H}^{+}}\] is:
A)
\[{{10}^{4}}\]
done
clear
B)
\[{{10}^{10}}\]
done
clear
C)
\[{{10}^{-4}}\]
done
clear
D)
\[{{10}^{-10}}\]
done
clear
View Answer play_arrow
question_answer 62) When sodium nitrate is heated above\[{{6000}^{o}}C\], then:
A)
only \[N{{a}_{2}}O\] is formed
done
clear
B)
only \[{{N}_{3}}\] is formed
done
clear
C)
only \[{{O}_{2}}\] is formed
done
clear
D)
all are formed
done
clear
View Answer play_arrow
question_answer 63) Which of the following produces \[C{{l}_{2}}\] gas?
A)
\[NaCl+HN{{O}_{3}}\]
done
clear
B)
\[Mn{{O}_{2}}+HCl\]
done
clear
C)
\[KMn{{O}_{4}}+HCl\]
done
clear
D)
\[HCl+HN{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 64) Which is correctly arranged as increasing size?
A)
\[F<O<C<Cl<Br\]
done
clear
B)
\[C<O<F<Cl<Br\]
done
clear
C)
\[Cl<Br<F<C<O\]
done
clear
D)
\[O<F<C<Cl<Br\]
done
clear
View Answer play_arrow
question_answer 65) \[N{{H}_{3}}\] is absorbed by:
A)
ozone
done
clear
B)
\[CaO\]
done
clear
C)
pyrargallol
done
clear
D)
\[CaC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 66) \[1.25\,\,g\]\[N{{H}_{3}}\] contains how many atoms?
A)
\[{{10}^{23}}\]
done
clear
B)
\[2\times {{10}^{23}}\]
done
clear
C)
\[6\times {{10}^{13}}\]
done
clear
D)
\[4\times {{10}^{23}}\]
done
clear
View Answer play_arrow
question_answer 67) Which of the following has smallest bond angle?
A)
Ethane
done
clear
B)
Ethene
done
clear
C)
Ethyne
done
clear
D)
Ethanol
done
clear
View Answer play_arrow
question_answer 68) Chloroform in air is oxidised to :
A)
\[CC{{l}_{4}}\]
done
clear
B)
dichloromethane
done
clear
C)
phosgene
done
clear
D)
oxygen
done
clear
View Answer play_arrow
question_answer 69) Gypsum is:
A)
\[CaS{{O}_{4}}\cdot 2{{H}_{2}}O\]
done
clear
B)
\[CaS{{O}_{4}}\cdot \frac{1}{2}{{H}_{2}}O\]
done
clear
C)
\[MgS{{O}_{4}}\cdot 2{{H}_{2}}O\]
done
clear
D)
\[CuS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 70) Which is not soluble in water?
A)
\[PbS{{O}_{4}}\]
done
clear
B)
\[CdS{{O}_{4}}\]
done
clear
C)
\[Bi{{(S{{O}_{4}})}_{2}}\]
done
clear
D)
\[CuS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 71) Which of the following is colour red?
A)
\[C{{u}_{2}}O\]
done
clear
B)
\[CuF\]
done
clear
C)
\[Zn{{F}_{2}}\]
done
clear
D)
\[ZnC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 72) How many unpaired electrons are present in\[[Cr{{(N{{H}_{3}})}_{5}}]B{{r}_{3}}\]?
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 73) \[S+\frac{3}{2}{{O}_{2}}\xrightarrow{{}}S{{O}_{3}}\Delta H=2x\],\[S{{O}_{2}}+\frac{1}{2}{{O}_{2}}\xrightarrow{{}}S{{O}_{3}}\Delta H=y\],then heat of formation of \[S{{O}_{2}}\] is:
A)
\[2x-y\]
done
clear
B)
\[2x+y\]
done
clear
C)
\[x+y\]
done
clear
D)
\[\frac{2x-y}{2}\]
done
clear
View Answer play_arrow
question_answer 74) Reagent (catalyst) used in Friedel-Craft's alkylation reaction is:
A)
\[AlC{{l}_{3}}\]
done
clear
B)
\[anhyd.\,\,AlC{{l}_{3}}\]
done
clear
C)
\[{{N}_{2}}\]
done
clear
D)
\[He\]
done
clear
View Answer play_arrow
question_answer 75) Catalyst used in making \[{{H}_{2}}S{{O}_{4}}\] in contact process is:
A)
\[{{V}_{2}}{{O}_{5}}\]
done
clear
B)
\[F{{e}_{2}}{{O}_{3}}\]
done
clear
C)
\[C{{r}_{2}}{{O}_{3}}\]
done
clear
D)
\[Cr{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 76) When acetamide is reacted with \[NaOBr\], then product formed is:
A)
ethanamine
done
clear
B)
methanamine
done
clear
C)
methanamide
done
clear
D)
ethanenitrile
done
clear
View Answer play_arrow
question_answer 77) Isocyanide is prepared by :
A)
Friedel Craft's reaction
done
clear
B)
Wurtz's reacdon
done
clear
C)
Williamson synthesis
done
clear
D)
Carbylamine reaction
done
clear
View Answer play_arrow
question_answer 78) If rate of diffusion of \[C{{H}_{4}}\] is twice than that of a gas\[x\], then its molecular mass is:
A)
\[64\,\,g\]
done
clear
B)
\[16\,\,g\]
done
clear
C)
\[32\,\,g\]
done
clear
D)
\[8\,\,g\]
done
clear
View Answer play_arrow
question_answer 79) Which one is not Lewis acid?
A)
\[Be{{F}_{2}}\]
done
clear
B)
\[SnC{{l}_{4}}\]
done
clear
C)
\[AlC{{l}_{3}}\]
done
clear
D)
\[B{{F}_{3}}\]
done
clear
View Answer play_arrow
question_answer 80) Natural gas mainly consists of:
A)
methane
done
clear
B)
butane
done
clear
C)
propane
done
clear
D)
ethane \[+\] octane
done
clear
View Answer play_arrow
question_answer 81) Phenol is treated with \[Zn\] to form:
A)
benzoic acid
done
clear
B)
benzyl alcohol
done
clear
C)
benzene
done
clear
D)
benzoquinone
done
clear
View Answer play_arrow
question_answer 82) Which one is isoelectronic with\[CO?\]
A)
\[N_{2}^{-}\]
done
clear
B)
\[N_{2}^{+}\]
done
clear
C)
\[C{{N}^{-}}\]
done
clear
D)
\[NO\]
done
clear
View Answer play_arrow
question_answer 83) How much volume of \[1\,\,M\,\,{{H}_{2}}S{{O}_{4}}\] is required to neutralize \[20\,\,mL\] of\[1M\,\,NaOH\]?
A)
\[10\,\,mL\]
done
clear
B)
\[20\,\,mL\]
done
clear
C)
\[5\,\,mL\]
done
clear
D)
\[15\,\,mL\]
done
clear
View Answer play_arrow
question_answer 84) Fenton's reagent is:
A)
\[SnC{{l}_{2}}+HCl\]
done
clear
B)
\[AgN{{O}_{3}}+N{{H}_{4}}OH\]
done
clear
C)
\[CuS{{O}_{4}}+NaOH\]
done
clear
D)
\[FeS{{O}_{4}}+{{H}_{2}}{{O}_{2}}\]
done
clear
View Answer play_arrow
question_answer 85) \[C{{u}^{2+}}+Ag\xrightarrow{{}}Cu+A{{g}^{+}}\] oxidation half reaction is:
A)
\[C{{u}^{2+}}\to Cu\]
done
clear
B)
\[Ag\to A{{g}^{+}}\]
done
clear
C)
\[Cu\to C{{u}^{2+}}\]
done
clear
D)
all of these
done
clear
View Answer play_arrow
question_answer 86) \[{{C}_{4}}{{H}_{10}}O\] has how many isomeric alcohols?
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 87) \[IUPAC\]name of\[C{{H}_{3}}-C\equiv C-HC-{{(C{{H}_{3}})}_{2}}\]is:
A)
4-methyl-2-pentyne
done
clear
B)
1, 1-dimethyl-2-butyne
done
clear
C)
2-methyl-4-pentyne
done
clear
D)
4, 4-dimethyl-2-butyne
done
clear
View Answer play_arrow
question_answer 88) Fehling test is given by:
A)
glucose
done
clear
B)
fructose
done
clear
C)
sucrose
done
clear
D)
all of these
done
clear
View Answer play_arrow
question_answer 89) Number of isomeric primary amine of molecular formula \[{{C}_{4}}{{H}_{11}}N\] is:
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 90) For reaction\[3X+Y{{X}_{3}}Y\]\[\Delta H=+ve\], amount of \[{{X}_{3}}Y\] can be changed by:
A)
changing temperature
done
clear
B)
changing pressure
done
clear
C)
changing temperature, pressure,
done
clear
D)
changing temperature, pressure, adding catalyst
done
clear
View Answer play_arrow
question_answer 91) Which one is most ionic?
A)
\[{{P}_{2}}{{O}_{5}}\]
done
clear
B)
\[Mn{{O}_{2}}\]
done
clear
C)
\[M{{n}_{2}}{{O}_{7}}\]
done
clear
D)
\[{{P}_{2}}{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 92) Which one gives \[{{I}_{2}}\] on reaction with\[KI?\]
A)
\[A{{g}_{2}}S{{O}_{4}}\]
done
clear
B)
\[CuS{{O}_{4}}\]
done
clear
C)
\[PbS{{O}_{4}}\]
done
clear
D)
\[CdS{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 93) Colour of the solution when \[KI\] reacts with \[B{{r}_{2}}\] is:
A)
blue
done
clear
B)
black
done
clear
C)
red
done
clear
D)
no change
done
clear
View Answer play_arrow
question_answer 94) Finely divided iron combines with \[CO\] to give:
A)
\[Fe{{(CO)}_{5}}\]
done
clear
B)
\[F{{e}_{2}}{{(CO)}_{9}}\]
done
clear
C)
\[F{{e}_{3}}{{(CO)}_{12}}\]
done
clear
D)
\[Fe{{(CO)}_{6}}\]
done
clear
View Answer play_arrow
question_answer 95) Which of the following is pyramidal?
A)
\[PC{{l}_{3}}\]
done
clear
B)
\[CO_{3}^{2-}\]
done
clear
C)
\[S{{O}_{2}}\]
done
clear
D)
\[NO_{3}^{-}\]
done
clear
View Answer play_arrow
question_answer 96) Which of the following conducts electricity?
A)
Crystal\[NaCl\]
done
clear
B)
Diamond
done
clear
C)
Molten\[KBr\]
done
clear
D)
Sulphur
done
clear
View Answer play_arrow
question_answer 97) Ratio of kinetic energy of hydrogen and helium gas at \[300\,\,K\] is:
A)
\[2:1\]
done
clear
B)
\[4:5\]
done
clear
C)
\[1:1\]
done
clear
D)
\[1:2\]
done
clear
View Answer play_arrow
question_answer 98) Which of the following has highest energy?
A)
\[n=2,\,\,l=1\]
done
clear
B)
\[n=3,\,\,l=2\]
done
clear
C)
\[n=3,\,\,l=1\]
done
clear
D)
\[n=2,\,\,l=0\]
done
clear
View Answer play_arrow
question_answer 99) Oxidation state of phosphorus in pyrophosphoric acid is:
A)
\[+5\]
done
clear
B)
\[+3\]
done
clear
C)
\[+4\]
done
clear
D)
\[+1\]
done
clear
View Answer play_arrow
question_answer 100) If the \[75%\] of a first order reaction is complete in\[8\min \], then time taken to decompose \[50%\] of its initial amount is:
A)
\[2\min \]
done
clear
B)
\[4\min \]
done
clear
C)
\[12\min \]
done
clear
D)
\[1\min \]
done
clear
View Answer play_arrow
question_answer 101) If\[a\ne \beta \]and\[{{\alpha }^{2}}=5\alpha -3,\,\,{{\beta }^{2}}=5\beta -3\]then the equation having \[\alpha /\beta \] and \[\beta /\alpha \] as its roots is:
A)
\[3{{x}^{2}}+19x+3=0\]
done
clear
B)
\[3{{x}^{2}}-19x+3=0\]
done
clear
C)
\[3{{x}^{2}}-19x-3=0\]
done
clear
D)
\[{{x}^{2}}-16x+1=0\]
done
clear
View Answer play_arrow
question_answer 102) If\[y={{(x+\sqrt{1+{{x}^{2}}})}^{n}}\], then\[{{(1+x)}^{2}}\frac{{{d}^{2}}y}{d{{x}^{2}}}+x\frac{dy}{dx}\]is
A)
\[{{n}^{2}}y\]
done
clear
B)
\[-{{n}^{2}}y\]
done
clear
C)
\[-y\]
done
clear
D)
\[2{{x}^{2}}y\]
done
clear
View Answer play_arrow
question_answer 103) If\[1,\,\,{{\log }_{3}}\sqrt{({{3}^{1-x}}+2)},\,\,{{\log }_{3}}(4\cdot {{3}^{x}}-1)\]are in \[AP\], then \[x\] equals:
A)
\[{{\log }_{3}}4\]
done
clear
B)
\[1-{{\log }_{3}}4\]
done
clear
C)
\[1-{{\log }_{4}}3\]
done
clear
D)
\[{{\log }_{4}}3\]
done
clear
View Answer play_arrow
question_answer 104) A problem in mathematics is given to three students \[A,\,\,\,B,\,\,\,C\] and their respective probability of solving the problem is \[\frac{1}{2},\,\,\,\frac{1}{3}\] and\[\frac{1}{4}\]. Probability that the problem is solved, is:
A)
\[\frac{3}{4}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
View Answer play_arrow
question_answer 105) The angle of elevation of a tower at a point distant \[d\] metres from its base is\[{{30}^{o}}\]. If the tower is \[20\,\,m\] high, then the value of \[d\] is:
A)
\[10\sqrt{3}m\]
done
clear
B)
\[\frac{20}{\sqrt{3}}m\]
done
clear
C)
\[20\sqrt{3}m\]
done
clear
D)
\[10\,\,m\]
done
clear
View Answer play_arrow
question_answer 106) \[l,\,\,\,m,\,\,\,n\] are the \[p\text{th}\], \[q\text{th}\] and \[r\text{th}\] terms of a \[GP\] and all positive, then\[\left| \begin{matrix} \log l & p & 1 \\ \log m & q & 1 \\ \log n & r & 1 \\ \end{matrix} \right|\]equals:
A)
\[3\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 107) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{1-\cos 2x}}{\sqrt{2}x}\]is equal to:
A)
\[\lambda \]
done
clear
B)
\[-1\]
done
clear
C)
zero
done
clear
D)
does not exist
done
clear
View Answer play_arrow
question_answer 108) A triangle with vertices\[(4,\,\,0),\,\,(-1,\,\,-1),\,\,(3,\,\,5)\] is:
A)
isosceles and right angled
done
clear
B)
isosceles but not right angled
done
clear
C)
right angled but not isosceles
done
clear
D)
neither right angled nor isosceles
done
clear
View Answer play_arrow
question_answer 109) \[{{\cot }^{-1}}(\sqrt{\cos \alpha })-{{\tan }^{-1}}(\sqrt{\cos \alpha })=x\], then\[\sin x\]is equal to:
A)
\[{{\tan }^{2}}\left( \frac{\alpha }{2} \right)\]
done
clear
B)
\[{{\cot }^{2}}\left( \frac{\alpha }{2} \right)\]
done
clear
C)
\[\tan \alpha \]
done
clear
D)
\[\cot \left( \frac{\alpha }{2} \right)\]
done
clear
View Answer play_arrow
question_answer 110) A plane which passes through the point \[(3,\,\,2,\,\,0)\] and the line\[\frac{x-3}{1}=\frac{y-6}{5}=\frac{z-4}{4}\]is:
A)
\[x-y+z=1\]
done
clear
B)
\[x+y+z=5\]
done
clear
C)
\[x+2y-z=1\]
done
clear
D)
\[2x-y+z=5\]
done
clear
View Answer play_arrow
question_answer 111) The solution of the equation \[\frac{{{d}^{2}}y}{d{{x}^{2}}}={{e}^{-2x}}\] is:
A)
\[\frac{{{e}^{-2x}}}{4}\]
done
clear
B)
\[\frac{{{e}^{-2x}}}{4}+cx+d\]
done
clear
C)
\[\frac{1}{4}{{e}^{-2x}}+c{{x}^{2}}+d\]
done
clear
D)
\[\frac{1}{4}{{e}^{-2x}}+c+d\]
done
clear
View Answer play_arrow
question_answer 112) \[\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{{{x}^{2}}+5x+3}{{{x}^{2}}+x+2} \right)}^{x}}\]is equal to:
A)
\[{{e}^{4}}\]
done
clear
B)
\[{{e}^{2}}\]
done
clear
C)
\[{{e}^{3}}\]
done
clear
D)
\[e\]
done
clear
View Answer play_arrow
question_answer 113) The domain of\[{{\sin }^{-1}}\left[ {{\log }_{3}}\left( \frac{x}{3} \right) \right]\]is:
A)
\[[1,\,\,9]\]
done
clear
B)
\[[-1,\,\,9]\]
done
clear
C)
\[[-9,\,\,1]\]
done
clear
D)
\[[-9,\,\,-1]\]
done
clear
View Answer play_arrow
question_answer 114) The value of\[{{2}^{1/4}}\cdot {{4}^{1/8}}\cdot {{8}^{1/16}}...\infty \]is
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 115) Fifth term of a \[GP\] is \[2\], then the product of its \[9\] terms is:
A)
256
done
clear
B)
512
done
clear
C)
1024
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 116) \[\int_{0}^{10\pi }{|\sin x|}\,\,dx\]is:
A)
\[20\]
done
clear
B)
\[8\]
done
clear
C)
\[10\]
done
clear
D)
\[18\]
done
clear
View Answer play_arrow
question_answer 117) \[{{I}_{n}}=\int_{0}^{\pi /4}{{{\tan }^{n}}x}\,\,dx\], then\[\underset{n\to \infty }{\mathop{\lim }}\,n[{{I}_{n}}+{{I}_{n+2}}]\] equal to:
A)
\[\frac{1}{2}\]
done
clear
B)
\[1\]
done
clear
C)
\[\infty \]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 118) \[\int_{-\pi }^{\pi }{\frac{2x(1+\sin x)}{1+{{\cos }^{2}}x}}dx\]is:
A)
\[\frac{{{\pi }^{2}}}{4}\]
done
clear
B)
\[{{\pi }^{2}}\]
done
clear
C)
\[zero\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 119) The period of the function\[f(x)={{\sin }^{4}}x+{{\cos }^{4}}x\] is:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[2\pi \]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 120) If\[{{x}^{y}}={{e}^{x-y}}\], then\[\frac{dy}{dx}\]is:
A)
\[\frac{1+x}{1+\log x}\]
done
clear
B)
\[\frac{1-\log x}{1+\log x}\]
done
clear
C)
not defined
done
clear
D)
\[\frac{\log x}{{{(1+\log x)}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 121) The two curves \[{{x}^{3}}-3x{{y}^{2}}+2=0\] and\[3{{x}^{2}}y-{{y}^{3}}-2=0\]
A)
cut at right angles
done
clear
B)
touch each other
done
clear
C)
cut at an angle\[\frac{\pi }{3}\]
done
clear
D)
cut at an angle\[\frac{\pi }{4}\]
done
clear
View Answer play_arrow
question_answer 122) The function \[f(x)={{\cot }^{-1}}x+x\] increases in the interval:
A)
\[(1,\,\,\infty )\]
done
clear
B)
\[(-1,\,\,\infty )\]
done
clear
C)
\[(-\infty ,\,\,\infty )\]
done
clear
D)
\[(0,\,\,\infty )\]
done
clear
View Answer play_arrow
question_answer 123) The greatest value of\[f(x)={{(x+1)}^{1/3}}-{{(x-1)}^{1/3}}\]on\[[0,\,\,1]\]is:
A)
\[1\]
done
clear
B)
\[2\]
done
clear
C)
\[3\]
done
clear
D)
\[1/3\]
done
clear
View Answer play_arrow
question_answer 124) \[\int{\frac{dx}{x({{x}^{n}}+1)}}\]is equal to:
A)
\[\frac{1}{n}\log \left( \frac{{{x}^{n}}}{{{x}^{n}}+1} \right)+c\]
done
clear
B)
\[\frac{1}{n}\log \left( \frac{{{x}^{n}}+1}{{{x}^{n}}} \right)+c\]
done
clear
C)
\[\log \left( \frac{{{x}^{n}}}{{{x}^{n}}+1} \right)+c\]
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 125) The area bounded by the curve \[y=2x-{{x}^{2}}\] and the straight line \[y=-x\] is given by:
A)
\[\frac{9}{2}sq\,\,unit\]
done
clear
B)
\[\frac{43}{6}sq\,\,unit\]
done
clear
C)
\[\frac{35}{6}sq\,\,unit\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 126) The differential equation of all non-vertical lines in a plane is:
A)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=0\]
done
clear
B)
\[\frac{{{d}^{2}}x}{d{{y}^{2}}}=0\]
done
clear
C)
\[\frac{dy}{dx}=0\]
done
clear
D)
\[\frac{dx}{dy}=0\]
done
clear
View Answer play_arrow
question_answer 127) Given two vectors \[\widehat{\mathbf{i}}-\widehat{\mathbf{j}}\] and \[\widehat{\mathbf{i}}+2\widehat{\mathbf{j}}\] the unit vector coplanar with the two vectors and perpendicular to first is:
A)
\[\pm \frac{1}{\sqrt{2}}(\widehat{\mathbf{i}}+\widehat{\mathbf{j}})\]
done
clear
B)
\[\frac{1}{\sqrt{5}}(2\widehat{\mathbf{i}}+\widehat{\mathbf{j}})\]
done
clear
C)
\[\pm \frac{1}{\sqrt{2}}(\widehat{\mathbf{i}}+\widehat{\mathbf{k}})\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 128) The vector \[\widehat{\mathbf{i}}+x\widehat{\mathbf{j}}+3\widehat{\mathbf{k}}\] is rotated through an angle \[\theta \] and doubled in magnitude, then it becomes\[4\widehat{\mathbf{i}}+(4x-2)\widehat{\mathbf{j}}+2\widehat{\mathbf{k}}\]. The value of is:
A)
\[\left\{ -\frac{2}{3},\,\,2 \right\}\]
done
clear
B)
\[\left\{ \frac{1}{3},\,\,2 \right\}\]
done
clear
C)
\[\left\{ \frac{2}{3},\,\,0 \right\}\]
done
clear
D)
\[\{2,\,\,7\}\]
done
clear
View Answer play_arrow
question_answer 129) A parallelepiped is formed by planes drawn through the points \[(2,\,\,3,\,\,5)\] and \[(5,\,\,9,\,\,7)\] parallel to the coordinate planes. The length of a diagonal of the parallelepiped to piped is:
A)
\[7\]
done
clear
B)
\[\sqrt{38}\]
done
clear
C)
\[\sqrt{155}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 130) The equation of the plane containing the line\[\frac{x-{{x}_{1}}}{l}=\frac{y-{{y}_{1}}}{m}=\frac{z-{{z}_{1}}}{n}\]is\[a(x-{{x}_{1}})+b(y-{{y}_{1}})+c(z-{{z}_{1}})=0\], where:
A)
\[a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}=0\]
done
clear
B)
\[al+bm+cn=0\]
done
clear
C)
\[\frac{a}{l}=\frac{b}{m}=\frac{c}{n}\]
done
clear
D)
\[l{{x}_{1}}+m{{y}_{1}}+n{{z}_{1}}=0\]
done
clear
View Answer play_arrow
question_answer 131) \[A\] and \[B\] play a game where each is asked to select a number from \[1\] to\[25\]. If the two numbers match, both of them win a prize. The probability that they will not win a prize in a single trial is:
A)
\[\frac{1}{25}\]
done
clear
B)
\[\frac{24}{25}\]
done
clear
C)
\[\frac{2}{25}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 132) The equation of the directrix of the parabola \[{{y}^{2}}+4y+4x+2=0\]is:
A)
\[x=-1\]
done
clear
B)
\[x=1\]
done
clear
C)
\[x=-\frac{3}{2}\]
done
clear
D)
\[x=\frac{3}{2}\]
done
clear
View Answer play_arrow
question_answer 133) Let \[{{T}_{n}}\] denote the number of triangles which can be formed using the vertices of a regular polygon of \[n\] sides. If\[{{T}_{n+1}}-{{T}_{n}}=21\], then n equals:
A)
\[5\]
done
clear
B)
\[7\]
done
clear
C)
\[6\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 134) In a triangle \[ABC\], \[\frac{A-B+C}{2}\]is equal to:
A)
\[{{a}^{2}}+{{b}^{2}}-{{c}^{2}}\]
done
clear
B)
\[{{c}^{2}}+{{a}^{2}}-{{b}^{2}}\]
done
clear
C)
\[{{b}^{2}}-{{c}^{2}}-{{a}^{2}}\]
done
clear
D)
\[{{c}^{2}}-{{a}^{2}}-{{b}^{2}}\]
done
clear
View Answer play_arrow
question_answer 135) For \[x\in R,\,\,\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{x-3}{x+2} \right)}^{x}}\] is equal to:
A)
\[e\]
done
clear
B)
\[{{e}^{-1}}\]
done
clear
C)
\[{{e}^{-5}}\]
done
clear
D)
\[{{e}^{5}}\]
done
clear
View Answer play_arrow
question_answer 136) The in centre of the triangle with vertices \[(1,\,\,\sqrt{3}),\,\,(0,\,\,0)\]and\[(2,\,\,0)\]is:
A)
\[\left( 1,\,\,\frac{\sqrt{3}}{2} \right)\]
done
clear
B)
\[\left( \frac{2}{3},\,\,\frac{1}{\sqrt{3}} \right)\]
done
clear
C)
\[\left( \frac{2}{3},\,\,\frac{\sqrt{3}}{2} \right)\]
done
clear
D)
\[\left( 1,\,\,\frac{1}{\sqrt{3}} \right)\]
done
clear
View Answer play_arrow
question_answer 137) If the vectors \[\overset{\to }{\mathop{\mathbf{a}}}\,,\,\,\,\overset{\to }{\mathop{\mathbf{b}}}\,\] and \[\overset{\to }{\mathop{\mathbf{c}}}\,\] from the sides \[BC,\,\,\,CA\] and \[AB\] respectively, of a triangle \[ABC\], then:
A)
\[\overset{\to }{\mathop{\mathbf{a}}}\,\cdot \overset{\to }{\mathop{\mathbf{b}}}\,+\overset{\to }{\mathop{\mathbf{b}}}\,\cdot \overset{\to }{\mathop{\mathbf{c}}}\,+\overset{\to }{\mathop{\mathbf{c}}}\,\cdot \overset{\to }{\mathop{\mathbf{b}}}\,=0\]
done
clear
B)
\[\overset{\to }{\mathop{\mathbf{a}}}\,\times \overset{\to }{\mathop{\mathbf{b}}}\,=\overset{\to }{\mathop{\mathbf{b}}}\,\times \overset{\to }{\mathop{\mathbf{c}}}\,=\overset{\to }{\mathop{\mathbf{c}}}\,\times \overset{\to }{\mathop{\mathbf{a}}}\,=0\]
done
clear
C)
\[\overset{\to }{\mathop{\mathbf{a}}}\,\cdot \overset{\to }{\mathop{\mathbf{b}}}\,=\overset{\to }{\mathop{\mathbf{b}}}\,\cdot \overset{\to }{\mathop{\mathbf{c}}}\,=\overset{\to }{\mathop{\mathbf{c}}}\,\cdot \overset{\to }{\mathop{\mathbf{a}}}\,=0\]
done
clear
D)
\[\overset{\to }{\mathop{\mathbf{a}}}\,\times \overset{\to }{\mathop{\mathbf{a}}}\,+\overset{\to }{\mathop{\mathbf{a}}}\,\times \overset{\to }{\mathop{\mathbf{c}}}\,+\overset{\to }{\mathop{\mathbf{c}}}\,\times \overset{\to }{\mathop{\mathbf{a}}}\,=0\]
done
clear
View Answer play_arrow
question_answer 138) If \[\omega \] is an imaginary cube root of unity, then \[{{(1+\omega -{{\omega }^{2}})}^{7}}\]equals:
A)
\[128\omega \]
done
clear
B)
\[-128\omega \]
done
clear
C)
\[128{{\omega }^{2}}\]
done
clear
D)
\[-128{{\omega }^{2}}\]
done
clear
View Answer play_arrow
question_answer 139) \[{{\sin }^{2}}\theta =\frac{4xy}{{{(x+y)}^{2}}}\]is true, if and only if:
A)
\[x+y\ne 0\]
done
clear
B)
\[x=y,\,\,x\ne 0,\,\,y\ne 0\]
done
clear
C)
\[x=y\]
done
clear
D)
\[x\ne 0,\,\,y\ne 0\]
done
clear
View Answer play_arrow
question_answer 140) The radius of the circle passing through the foci of the ellipse \[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{9}=1\] and having its centre at\[(0,\,\,3)\] is:
A)
\[4\]
done
clear
B)
\[3\]
done
clear
C)
\[\sqrt{12}\]
done
clear
D)
\[\frac{7}{2}\]
done
clear
View Answer play_arrow
question_answer 141) If \[(\omega \ne 1)\] is a cubic root of unity, then\[\left| \begin{matrix} 1 & 1+1+{{\omega }^{2}} & {{\omega }^{2}} \\ 1-i & -1 & {{\omega }^{2}}-1 \\ -i & -1+\omega -i & -1 \\ \end{matrix} \right|\]equals:
A)
\[zero\]
done
clear
B)
\[1\]
done
clear
C)
\[i\]
done
clear
D)
\[\omega \]
done
clear
View Answer play_arrow
question_answer 142) Let\[f(2)=4\] and \[f'(2)=4\]. Then\[\underset{x\to 2}{\mathop{\lim }}\,\frac{x\,\,f(2)-2f(x)}{x-2}\]is given by:
A)
\[2\]
done
clear
B)
\[-2\]
done
clear
C)
\[-4\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 143) Three straight lines \[2x+11y-5=0\],\[24x+7y-20=0\]and\[4x-3y-2=0\]:
A)
form a triangle
done
clear
B)
are only concurrent
done
clear
C)
are concurrent with on line bisecting the angle between the other two
done
clear
D)
none of the above
done
clear
View Answer play_arrow
question_answer 144) A straight line through the point\[(2,\,\,2)\]intersects the line\[\sqrt{3}x+y=0\]and\[\sqrt{3}x-y=0\]at the points\[A\]and\[B\]. The equation to the line\[AB\], so that triangle\[AOB\]is equilateral is:
A)
\[x-2=0\]
done
clear
B)
\[y-2=0\]
done
clear
C)
\[x+y-4=0\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 145) The greatest distance of the point \[P(10,\,\,7)\] from the circle \[{{x}^{2}}+{{y}^{2}}-4x-2y-20=0\] is:
A)
\[10\]
done
clear
B)
\[15\]
done
clear
C)
\[5\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 146) The equation of the ellipse whose foci are \[(\pm \,\,2,\,\,0)\]and eccentricity \[\frac{1}{2}\] is:
A)
\[\frac{{{x}^{2}}}{12}+\frac{{{y}^{2}}}{16}=1\]
done
clear
B)
\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{12}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{8}=1\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 147) The equation of the chord joining two points \[({{x}_{1}},\,\,{{y}_{1}})\] and \[({{x}_{2}},\,\,{{y}_{2}})\] on the rectangular hyperbola \[xy={{c}^{2}}\] is:
A)
\[\frac{x}{{{x}_{1}}+{{x}_{2}}}+\frac{y}{{{y}_{1}}+{{y}_{2}}}=1\]
done
clear
B)
\[\frac{x}{{{x}_{1}}-{{x}_{2}}}+\frac{y}{{{y}_{1}}-{{y}_{2}}}=1\]
done
clear
C)
\[\frac{x}{{{y}_{1}}+{{y}_{2}}}+\frac{y}{{{x}_{1}}+{{x}_{2}}}=1\]
done
clear
D)
\[\frac{x}{{{y}_{1}}-{{y}_{2}}}+\frac{y}{{{x}_{1}}-{{x}_{2}}}=1\]
done
clear
View Answer play_arrow
question_answer 148) Let \[R\] be the resultant of \[P\] and \[Q\] \[\text{and}\] if \[\frac{P}{3}=\frac{Q}{7}=\frac{R}{5}\], the angle between \[P\] and \[R\] is:
A)
\[{{\cos }^{-1}}\left( \frac{11}{14} \right)\]
done
clear
B)
\[{{\cos }^{-1}}\left( -\frac{11}{14} \right)\]
done
clear
C)
\[\frac{2\pi }{3}\]
done
clear
D)
\[\frac{5\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 149) Two bodies of different masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are dropped from different heights \[{{h}_{1}}\] and \[{{h}_{2}}\]. The ratio of the time taken by the two bodies to fall through these distances is:
A)
\[{{h}_{1}}:{{h}_{2}}\]
done
clear
B)
\[\sqrt{{{h}_{1}}}:\sqrt{{{h}_{2}}}\]
done
clear
C)
\[h_{1}^{2}:h_{2}^{2}\]
done
clear
D)
\[{{h}_{2}}:{{h}_{1}}\]
done
clear
View Answer play_arrow
question_answer 150) If\[\operatorname{var}(x)=8.25,\,\,\operatorname{var}(y)=33.96\]and\[\operatorname{cov}(x,\,\,y)=10.2\], then the correlation coefficient is:
A)
\[0.89\]
done
clear
B)
\[-0.98\]
done
clear
C)
\[0.61\]
done
clear
D)
\[-0.16\]
done
clear
View Answer play_arrow