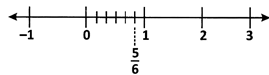
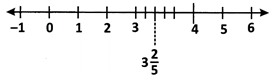
 (ii) Rational numbers of the form \[\frac{m}{n}\] where m > n are represented on the number line as shown below.
(ii) Rational numbers of the form \[\frac{m}{n}\] where m > n are represented on the number line as shown below.
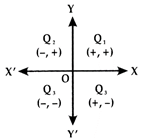 (i) \[{{Q}_{1}}\]is the I quadrant? Here both x and y are positive i.e., x > 0 and y > 0. The ordered pair (a, b) belongs to this quadrant.
(ii) \[{{Q}_{2}}\]is the II quadrant. Here x is negative and y is positive i.e., x < 0 and y > 0. The ordered pair (-a, b) belongs to this quadrant.
(iii) \[{{Q}_{3}}\]is the III quadrant. Here both x and y are negative, i.e., x < 0 and y < 0. The ordered pair (-a,- b) belongs to the quadrant,
(iv) \[{{Q}_{4}}\]is the IV quadrant. Here x is positive and y is negative i.e., x > 0 and y < 0. The ordered pair (a, -b) belongs to this quadrant.
(i) \[{{Q}_{1}}\]is the I quadrant? Here both x and y are positive i.e., x > 0 and y > 0. The ordered pair (a, b) belongs to this quadrant.
(ii) \[{{Q}_{2}}\]is the II quadrant. Here x is negative and y is positive i.e., x < 0 and y > 0. The ordered pair (-a, b) belongs to this quadrant.
(iii) \[{{Q}_{3}}\]is the III quadrant. Here both x and y are negative, i.e., x < 0 and y < 0. The ordered pair (-a,- b) belongs to the quadrant,
(iv) \[{{Q}_{4}}\]is the IV quadrant. Here x is positive and y is negative i.e., x > 0 and y < 0. The ordered pair (a, -b) belongs to this quadrant.
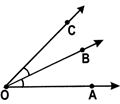
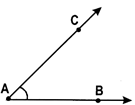 The angle formed by the two rays \[\overline{AB}\,\,and\,\,\overline{AC}\text{ }is\text{ }\angle BAC\text{ }or\text{ }\angle CAB.~\]called \[\overline{AB}\,\,and\,\,\overline{AC}\]are called the arms and the common initial point ‘A’ is called the vertex of the angle.
The angle formed by the two rays \[\overline{AB}\,\,and\,\,\overline{AC}\text{ }is\text{ }\angle BAC\text{ }or\text{ }\angle CAB.~\]called \[\overline{AB}\,\,and\,\,\overline{AC}\]are called the arms and the common initial point ‘A’ is called the vertex of the angle.
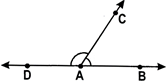
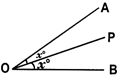 e.g., In the adjacent figure, the line OP divides \[\angle \]AOB into two
Equal parts.
\[\angle AOP=\angle POB={{\operatorname{x}}^{o}}\]
So, the line OP is ‘called the bisector of \[\angle \]AOB.
e.g., In the adjacent figure, the line OP divides \[\angle \]AOB into two
Equal parts.
\[\angle AOP=\angle POB={{\operatorname{x}}^{o}}\]
So, the line OP is ‘called the bisector of \[\angle \]AOB.
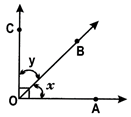 Here\[\angle x+\angle y={{90}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\] Complementary angles:
(ii) Supplementary angles: Two angles are said to be supplementary if the sum of their measures isequal to\[{{180}^{o}}\].
Here\[\angle x+\angle y={{90}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\] Complementary angles:
(ii) Supplementary angles: Two angles are said to be supplementary if the sum of their measures isequal to\[{{180}^{o}}\].
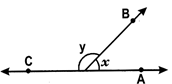 Here \[\angle x+\angle y={{180}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\]
Supplementary angles.
Here \[\angle x+\angle y={{180}^{o}},\]therefore \[\angle x\,\operatorname{and}\,\angle y\]
Supplementary angles.

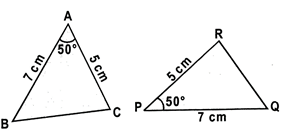 \[\Delta ABC=\Delta PQR\]
\[Since=PQ=7cm,\text{ }\angle C=PR=5cm\,\,and\,\angle A=\angle P=50{}^\circ .\]corresponding sides and angles of the other triangle.
(ii) A.S.A. congruence rule: Two e.g., triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle.
\[\Delta ABC=\Delta PQR\]
\[Since=PQ=7cm,\text{ }\angle C=PR=5cm\,\,and\,\angle A=\angle P=50{}^\circ .\]corresponding sides and angles of the other triangle.
(ii) A.S.A. congruence rule: Two e.g., triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle.
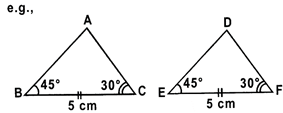 \[\Delta ABC\cong \Delta DEF\]
\[\angle B=\angle E={{45}^{o}},\angle C=\angle F=30{}^\circ \text{ }and\text{ }BC\text{ }=\text{ }EF\text{ }=\text{ }5cm.\]
(iii) S.S.S. congruence rule: If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
\[\Delta ABC=\Delta XYZ\]
\[\Delta ABC\cong \Delta DEF\]
\[\angle B=\angle E={{45}^{o}},\angle C=\angle F=30{}^\circ \text{ }and\text{ }BC\text{ }=\text{ }EF\text{ }=\text{ }5cm.\]
(iii) S.S.S. congruence rule: If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
\[\Delta ABC=\Delta XYZ\]
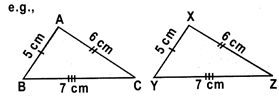 Since AB = XY = 5 cm, BC = YZ = 7 cm and CA = ZX = 6 cm.
Since AB = XY = 5 cm, BC = YZ = 7 cm and CA = ZX = 6 cm.
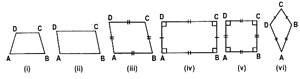 (i) Trapezium:
(a) A quadrilateral having exactly one pair of parallel sides is called a trapezium.
(b) A trapezium is said to be an isosceles trapezium if its non-parallel sides are equal.
ABCD is a trapezium in which AB || DC.
This trapezium is said to be an isosceles trapezium if AB || DC and AD = BC.
(ii) Parallelogram: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
ABCD is a parallelogram in which AB || DC and AD II BC.
Properties:
(a) In a parallelogram, any two opposite sides are equal.
(b) In a parallelogram, any two opposite angles are equal.
(c)In a parallelogram, the diagonals bisect each other.
(d) In a parallelogram, each diagonal divides it into two congruent triangles.
(e) In a parallelogram, any two adjacent angles have their sum equal to \[{{180}^{o}}\] i.e. the adjacent angles are supplementary.
(iii) Rhombus: A quadrilateral having all sides equal is called a rhombus.
ABCD is a rhombus in which AB II DC, AD || BC and AB = BC = CD = DA.
Properties:
(a) The diagonals of a rhombus bisect each other at right angles.
(b) Each diagonal of a rhombus divides it into two congruent triangles.
(c) Opposite angles of a rhombus are equal and the sum of any two adjacent angles is\[{{180}^{o}}\]
(d) The opposite sides of a rhombus are parallel.
(e) All the sides of a rhombus are equal.
(iv) Rectangle: A parallelogram whose angles are all right angles is called a rectangle.
ABCD is a rectangle in which,
AD || BC and AB || CD and
\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]
(i) Trapezium:
(a) A quadrilateral having exactly one pair of parallel sides is called a trapezium.
(b) A trapezium is said to be an isosceles trapezium if its non-parallel sides are equal.
ABCD is a trapezium in which AB || DC.
This trapezium is said to be an isosceles trapezium if AB || DC and AD = BC.
(ii) Parallelogram: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
ABCD is a parallelogram in which AB || DC and AD II BC.
Properties:
(a) In a parallelogram, any two opposite sides are equal.
(b) In a parallelogram, any two opposite angles are equal.
(c)In a parallelogram, the diagonals bisect each other.
(d) In a parallelogram, each diagonal divides it into two congruent triangles.
(e) In a parallelogram, any two adjacent angles have their sum equal to \[{{180}^{o}}\] i.e. the adjacent angles are supplementary.
(iii) Rhombus: A quadrilateral having all sides equal is called a rhombus.
ABCD is a rhombus in which AB II DC, AD || BC and AB = BC = CD = DA.
Properties:
(a) The diagonals of a rhombus bisect each other at right angles.
(b) Each diagonal of a rhombus divides it into two congruent triangles.
(c) Opposite angles of a rhombus are equal and the sum of any two adjacent angles is\[{{180}^{o}}\]
(d) The opposite sides of a rhombus are parallel.
(e) All the sides of a rhombus are equal.
(iv) Rectangle: A parallelogram whose angles are all right angles is called a rectangle.
ABCD is a rectangle in which,
AD || BC and AB || CD and
\[\angle A=\angle B=\angle C=\angle D={{90}^{o}}\]
You need to login to perform this action.
You will be redirected in
3 sec
