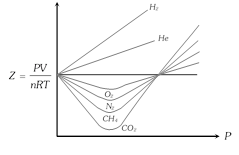
 (4) It is difficult to determine quantitatively the deviation of a real gas from ideal gas behaviour from the P-V isotherm curve as shown above. Compressibility factor Z defined by the equation,
\[PV=ZnRT\] or \[Z=PV/nRT=P{{V}_{m}}/RT\]
is more suitable for a quantitative description of the deviation from ideal gas behaviour.
(5) Greater is the departure of Z from unity, more is the deviation from ideal behaviour. Thus, when
(i) \[Z=1\], the gas is ideal at all temperatures and pressures. In case of \[{{N}_{2}}\], the value of Z is close to 1 at \[{{50}^{o}}C\]. This temperature at which a real gas exhibits ideal behaviour, for considerable range of pressure, is known as Boyle's temperature or Boyle's point \[({{T}_{B}})\].
(ii) \[Z>1\], the gas is less compressible than expected from ideal behaviour and shows positive deviation, usual at high P i.e. \[PV>RT\].
(iii) \[Z<1\], the gas is more compressible than expected from ideal behaviour and shows negative deviation, usually at low P i.e. \[PV<RT\].
(iv) \[Z>1\] for \[{{H}_{2}}\] and He at all pressure i.e., always shows positive deviation.
(v) The most easily liquefiable and highly soluble gases \[(N{{H}_{3}},\,S{{O}_{2}})\] show larger deviations from ideal behaviour i.e. \[Z<<1\].
(vi) Some gases like \[C{{O}_{2}}\] show both negative and positive deviation.
(6) Causes of deviations of real gases from ideal behaviour : The ideal gas laws can be derived from the kinetic theory of gases which is based on the following two important assumptions,
(i) The volume occupied by the molecules is negligible in comparison to the total volume of gas.
(ii) The molecules exert no forces of attraction upon one another. It is because neither of these assumptions can be regarded as applicable to real gases that the latter show departure from the ideal behaviour.
(4) It is difficult to determine quantitatively the deviation of a real gas from ideal gas behaviour from the P-V isotherm curve as shown above. Compressibility factor Z defined by the equation,
\[PV=ZnRT\] or \[Z=PV/nRT=P{{V}_{m}}/RT\]
is more suitable for a quantitative description of the deviation from ideal gas behaviour.
(5) Greater is the departure of Z from unity, more is the deviation from ideal behaviour. Thus, when
(i) \[Z=1\], the gas is ideal at all temperatures and pressures. In case of \[{{N}_{2}}\], the value of Z is close to 1 at \[{{50}^{o}}C\]. This temperature at which a real gas exhibits ideal behaviour, for considerable range of pressure, is known as Boyle's temperature or Boyle's point \[({{T}_{B}})\].
(ii) \[Z>1\], the gas is less compressible than expected from ideal behaviour and shows positive deviation, usual at high P i.e. \[PV>RT\].
(iii) \[Z<1\], the gas is more compressible than expected from ideal behaviour and shows negative deviation, usually at low P i.e. \[PV<RT\].
(iv) \[Z>1\] for \[{{H}_{2}}\] and He at all pressure i.e., always shows positive deviation.
(v) The most easily liquefiable and highly soluble gases \[(N{{H}_{3}},\,S{{O}_{2}})\] show larger deviations from ideal behaviour i.e. \[Z<<1\].
(vi) Some gases like \[C{{O}_{2}}\] show both negative and positive deviation.
(6) Causes of deviations of real gases from ideal behaviour : The ideal gas laws can be derived from the kinetic theory of gases which is based on the following two important assumptions,
(i) The volume occupied by the molecules is negligible in comparison to the total volume of gas.
(ii) The molecules exert no forces of attraction upon one another. It is because neither of these assumptions can be regarded as applicable to real gases that the latter show departure from the ideal behaviour.
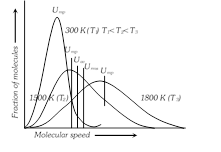 (4) Types of molecular speeds or Velocities
(i) Root mean square velocity \[({{u}_{rms}})\] : It is the square root of the mean of the squares of the velocity of a large number of molecules of the same gas.
\[{{u}_{rms}}=\sqrt{\frac{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+.....u_{n}^{2}}{n}}\]
\[{{u}_{rms}}=\sqrt{\frac{3PV}{(m{{N}_{0}})=M}}=\sqrt{\frac{3RT}{(m{{N}_{0}})=M}}\]\[=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3P}{d}}\]
where k = Boltzmann constant \[=\frac{R}{{{N}_{0}}}\]
(a) For the same gas at two different temperatures, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{T}_{1}}}{{{T}_{2}}}}\]
(b) For two different gases at the same temperature, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{M}_{2}}}{{{M}_{1}}}}\]
(c) RMS velocity at any temperature \[{{t}^{o}}C\] may be related to its value at S.T.P. as, \[{{u}_{t}}=\sqrt{\frac{3P(273+t)}{273d}}\].
(ii) Average velocity \[({{v}_{av}})\] : It is the average of the various velocities possessed by the molecules.
\[{{v}_{av}}=\frac{{{v}_{1}}+{{v}_{2}}+{{v}_{3}}+......{{v}_{n}}}{n}\]; \[{{v}_{av}}=\sqrt{\frac{8RT}{\pi M}}=\sqrt{\frac{8kT}{\pi m}}\]
(iii) Most probable velocity \[({{\alpha }_{mp}})\]: It is the velocity possessed by maximum number of molecules of a gas at a given temperature.
\[{{\alpha }_{mp}}=\sqrt{\frac{2RT}{M}}=\sqrt{\frac{2PV}{M}}=\sqrt{\frac{2P}{d}}\]
(5) Relation between molecular speeds or velocities,
(i) Relation between \[{{u}_{rms}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=0.9213\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.085\times {{v}_{av}}\]
(ii) Relation between \[{{\alpha }_{mp}}\] and \[{{u}_{rms}}\]: \[{{\alpha }_{mp}}=0.816\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.224\times {{\alpha }_{mp}}\]
(iii) Relation between \[{{\alpha }_{mp}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=1.128\times {{\alpha }_{mp}}\]
(iv) Relation between \[{{\alpha }_{mp}}\], \[{{v}_{av}}\] and \[{{u}_{rms}}\]
\[{{\alpha }_{mp}}\] : \[{{v}_{av}}\] : \[{{u}_{rms}}\]
\[\sqrt{\frac{2RT}{M}}\] : \[\sqrt{\frac{8RT}{\pi M}}\] : \[\sqrt{\frac{3RT}{M}}\]
\[\sqrt{2}\] : \[\sqrt{\frac{8}{\pi }}\] : \[\sqrt{3}\]
1.414 : 1.595 : 1.732
1 : 1.128 : 1.224
i.e., \[{{\alpha }_{mp}}<{{v}_{av}}<{{u}_{rms}}\]
(4) Types of molecular speeds or Velocities
(i) Root mean square velocity \[({{u}_{rms}})\] : It is the square root of the mean of the squares of the velocity of a large number of molecules of the same gas.
\[{{u}_{rms}}=\sqrt{\frac{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+.....u_{n}^{2}}{n}}\]
\[{{u}_{rms}}=\sqrt{\frac{3PV}{(m{{N}_{0}})=M}}=\sqrt{\frac{3RT}{(m{{N}_{0}})=M}}\]\[=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3P}{d}}\]
where k = Boltzmann constant \[=\frac{R}{{{N}_{0}}}\]
(a) For the same gas at two different temperatures, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{T}_{1}}}{{{T}_{2}}}}\]
(b) For two different gases at the same temperature, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{M}_{2}}}{{{M}_{1}}}}\]
(c) RMS velocity at any temperature \[{{t}^{o}}C\] may be related to its value at S.T.P. as, \[{{u}_{t}}=\sqrt{\frac{3P(273+t)}{273d}}\].
(ii) Average velocity \[({{v}_{av}})\] : It is the average of the various velocities possessed by the molecules.
\[{{v}_{av}}=\frac{{{v}_{1}}+{{v}_{2}}+{{v}_{3}}+......{{v}_{n}}}{n}\]; \[{{v}_{av}}=\sqrt{\frac{8RT}{\pi M}}=\sqrt{\frac{8kT}{\pi m}}\]
(iii) Most probable velocity \[({{\alpha }_{mp}})\]: It is the velocity possessed by maximum number of molecules of a gas at a given temperature.
\[{{\alpha }_{mp}}=\sqrt{\frac{2RT}{M}}=\sqrt{\frac{2PV}{M}}=\sqrt{\frac{2P}{d}}\]
(5) Relation between molecular speeds or velocities,
(i) Relation between \[{{u}_{rms}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=0.9213\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.085\times {{v}_{av}}\]
(ii) Relation between \[{{\alpha }_{mp}}\] and \[{{u}_{rms}}\]: \[{{\alpha }_{mp}}=0.816\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.224\times {{\alpha }_{mp}}\]
(iii) Relation between \[{{\alpha }_{mp}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=1.128\times {{\alpha }_{mp}}\]
(iv) Relation between \[{{\alpha }_{mp}}\], \[{{v}_{av}}\] and \[{{u}_{rms}}\]
\[{{\alpha }_{mp}}\] : \[{{v}_{av}}\] : \[{{u}_{rms}}\]
\[\sqrt{\frac{2RT}{M}}\] : \[\sqrt{\frac{8RT}{\pi M}}\] : \[\sqrt{\frac{3RT}{M}}\]
\[\sqrt{2}\] : \[\sqrt{\frac{8}{\pi }}\] : \[\sqrt{3}\]
1.414 : 1.595 : 1.732
1 : 1.128 : 1.224
i.e., \[{{\alpha }_{mp}}<{{v}_{av}}<{{u}_{rms}}\]
 (2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\] where n is the number of molecules per unit molar volume, \[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by, \[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]where, \[{{\sigma }_{AB}}=\frac{{{\sigma }_{A}}+{{\sigma }_{B}}}{2}\]
\[{{M}_{A}}\], \[{{M}_{B}}\] are molecular weights \[(M=m{{N}_{0}})\]
(iv) (a) At particular temperature; \[Z\propto {{p}^{2}}\]
(b) At particular pressure; \[Z\propto {{T}^{-3/2}}\]
(c) At particular volume; \[Z\propto {{T}^{1/2}}\]
(3) During molecular collisions a molecule covers a small distance before it gets deflected. The average distance travelled by the gas molecules between two successive collision is called mean free path \[(\lambda )\].
\[\lambda =\frac{\text{Average distance travelled per unit time(}{{u}_{\text{av}}}\text{)}}{\text{No}\text{. of collisions made by single molecule per unit time (}{{Z}_{A}}\text{)}}\]
\[=\frac{{{u}_{\text{av}}}}{\sqrt{\text{2}}\pi {{\sigma }^{2}}{{u}_{\text{avr}\text{.}}}n}=\frac{1}{\sqrt{2}\pi n{{\sigma }^{2}}}\]
(i) Larger the size of the molecules, smaller the mean free path, i.e., \[\lambda \propto \frac{1}{{{\text{(radius)}}^{\text{2}}}}\]
(ii) Greater the number of molecules per unit volume, smaller the mean free path.
(iii) Larger the temperature, larger the mean free path.
(iv) Larger the pressure, smaller the mean free path.
(5) Relation between collision frequency (Z) and mean free path (l) is given by, \[Z=\frac{{{u}_{rms}}}{\lambda }\]
(2) The number of collisions taking place in unit time per unit volume, called collision frequency (z).
(i) The number of collision made by a single molecule with other molecules per unit time are given by, \[{{Z}_{A}}=\sqrt{2}\pi {{\sigma }^{2}}{{u}_{\text{av}\text{.}}}n\] where n is the number of molecules per unit molar volume, \[n=\frac{\text{Avogadro number(}{{N}_{0}}\text{)}}{{{V}_{m}}}=\frac{6.02\times {{10}^{23}}}{0.0224}{{m}^{-3}}\]
(ii) The total number of bimolecular collision per unit time are given by, \[{{Z}_{AA}}=\frac{1}{\sqrt{2}}\pi {{\sigma }^{2}}{{u}_{\text{av}.}}{{n}^{2}}\]
(iii) If the collisions involve two unlike molecules, the number of bimolecular collision are given by, \[{{Z}_{AB}}=\sigma _{AB}^{2}{{\left[ 8\pi RT\frac{({{M}_{A}}+{{M}_{B}})}{{{M}_{A}}{{M}_{B}}} \right]}^{1/2}}\]where, \[{{\sigma }_{AB}}=\frac{{{\sigma }_{A}}+{{\sigma }_{B}}}{2}\]
\[{{M}_{A}}\], \[{{M}_{B}}\] are molecular weights \[(M=m{{N}_{0}})\]
(iv) (a) At particular temperature; \[Z\propto {{p}^{2}}\]
(b) At particular pressure; \[Z\propto {{T}^{-3/2}}\]
(c) At particular volume; \[Z\propto {{T}^{1/2}}\]
(3) During molecular collisions a molecule covers a small distance before it gets deflected. The average distance travelled by the gas molecules between two successive collision is called mean free path \[(\lambda )\].
\[\lambda =\frac{\text{Average distance travelled per unit time(}{{u}_{\text{av}}}\text{)}}{\text{No}\text{. of collisions made by single molecule per unit time (}{{Z}_{A}}\text{)}}\]
\[=\frac{{{u}_{\text{av}}}}{\sqrt{\text{2}}\pi {{\sigma }^{2}}{{u}_{\text{avr}\text{.}}}n}=\frac{1}{\sqrt{2}\pi n{{\sigma }^{2}}}\]
(i) Larger the size of the molecules, smaller the mean free path, i.e., \[\lambda \propto \frac{1}{{{\text{(radius)}}^{\text{2}}}}\]
(ii) Greater the number of molecules per unit volume, smaller the mean free path.
(iii) Larger the temperature, larger the mean free path.
(iv) Larger the pressure, smaller the mean free path.
(5) Relation between collision frequency (Z) and mean free path (l) is given by, \[Z=\frac{{{u}_{rms}}}{\lambda }\]
You need to login to perform this action.
You will be redirected in
3 sec
