BOOK ? DINESH
MATHEMATICS
1. Relations
and Functions
NCERT TEXT
BOOKS EXERCISE 1.1
E1. Determine whether each of the following
relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3, ? 13, 14}
defined as R = {x, y} : 3x ? y = 0}
(ii) Relation R in the set N of natural numbers
defined as R = {x, y) : y = x + 5 and x < 4}
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6}
as
R = {(x, y) : y is divisible by x}
(iv) Relation R in the set X of all integers
defined as
R = {(x, y) : x ? y is an integer}
(v) Relation R in the set A of human beings in a
town at a particular time given by
(a) R = {(x, y) : x and y work at the same
place}
(b) R = {(x, y) : x and y live in the same
locality}
(c) R = {(x, y) : x is exactly 7 cm taller
than y}
(d) R = {(x, y) : x is father of y}
(e) R = {(x, y) : x is father of y}
Sol. (i) A = {1, 2, 3, 4, ??. 13, 14:}
R = {(x, y) : 3x ? y = 0 i.e. y = 3x}

R = {(1, 3),
(2, 6), (3, 9), (4, 12)}
Reflexive : As 1
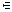
A but (1, 1)
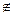
R.

R is not
reflexive.
Symmetric : As (1, 3)
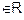
but
(3, 1)
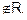

R is not
symmetric.
Transitive : As (1, 3)
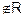
and
(3, 9)
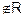
but (1, 9)
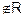
,

R is not
transitive.
Hence relation R is neither reflexive, nor
symmetric, nor transitive.
(ii) N = {1, 2, 3, 4, 5 6 ??}
R = {(x, y) : y = x + 5 and x < 4}
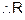
= {(1, 6),
(2, 7), (3, 8)}
Reflexive : As
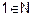
but (1, 1),
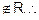
is
not reflexive.
Symmetric : As (1, 6)
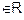
but
(6, 1)
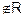
.
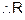
is not
symmetric.
Transitive : Clearly R is transitive
since it is not contradicted here.
Hence relation R is transitive but neither
reflexive nor symmetric.
(iii)
A = {1, 2, 3, 4, 5, 6}
R = {(x, y) : y is divisible by x}

R = {(1, 1),
(2, 2), (3, 3), (4, 4), (5, 5), (6, 6),
(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 4), (2, 6), (3, 6)}
Reflexive : As (a, a)
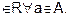
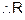
is reflexive
Symmetric : A (1, 2)
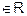
but (2, 1)
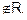
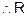
is not
symmetric.
Transitive : As (a, b)
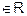
and (b, c)
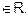
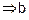
is divisible
by a and c is divisible by b
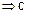
is divisible
by
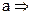
(a, c)
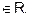
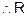
is
transitive.
Hence relation R is reflexive, transitive but not symmetric.
(iv) Z = {?.., ?3, ?2, ?1, 0, 1, 2, 3, ?}
R = {(x, y) : x ? y is an integer.
Reflexive : As a ? a = 0 is an integer
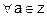
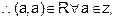
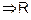
is symmetric.
Symmetric : As a ? b and b ? a are integers
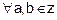
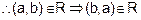
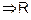
is symmetric.
Transitive : As a ? b and b ? c are integers and
(a ? b) + (b ? c) = a ? c is also an integer.
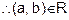
and (b, c)
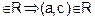
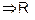
is transitive.
Hence R is reflexive, symmetric and transitive.
(v) (a) Clearly R is reflexive, symmetry and transitive. (b)
Clearly R is reflexive, symmetric and transitive.
(c) A = {x : x is human being in a town}
R = {(x, y) : x is exactly 7 cm taller than y}
Reflexive : As a is not 7 cm taller than a.
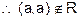
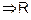
is not
reflexive.
Symmetric : If a is exactly 7 cm taller than
b, then b cannot be 7 cm taller, than a
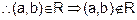

R is not
symmetric.
Transitive : If a exactly 7 cm taller
than b and b is exactly 7 cm taller than c then a is exactly 14 cm taller than
c.
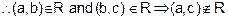
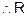
is not
transitive.
Hence R is neither reflexive, nor symmetric
nor transitive.
(d) A = {x : x is human being}
R = {(x, y) : x is a wife of y}
Reflexive : As a is not wife of
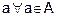
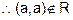
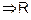
is not
reflexive.
Symmetric : If a is a wife of b then b cannot
be wife of a.
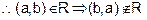

R is not
symmetric.
Transitive : If a is a wife of b then b
is a male ad a male cannot be a wife.

(a, b)
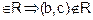

R is
transitive as it is not contradicted here.

R is
transitive but neither reflexive nor symmetric.
(e) Clearly R is neither reflexive nor
symmetric nor transitive.
E2. Show that the relation R in the set R of
real numbers, defined as R = {(a, b) : a
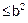
} is neither
reflexive nor symmetric nor transitive.
Sol. R = {(a, b) : a
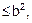
a,
b,
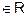
}
Reflexive :
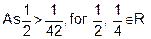
i.e.
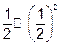

(a, a)
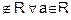
Hence R is not reflexive.
Symmetric : As 2, 5
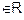
and
2 < 25 i.e. 2 < 52.

(2, 5)
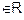
But
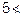
4 i.e.
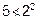
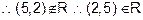
but (5, 2)
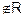
Hence R is not symmetric.
Transitive : As 3, ?2 and ?1
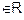
and
3 < (2)2 and ?2 < (?1)2.
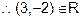
and (?2,
?1)
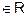
But
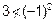
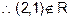
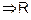
is not
symmetric.
Transitive : (a, b)
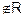
and
(b, c)
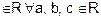
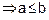
and
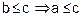
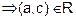
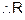
is
transitive.
Hence R is reflexive and transitive but not
symmetric.
Example E 3.
Check whether the relation R defined in the set {1,2, 3,4,
5, 6} as
R = {(a, b) : b = a + 1} is reflexive,
symmetric or transitive.
Sol. t A = {1, 2, 3,
4, 5. 6}
R = {(a,
b) : b = a + 1, a, b
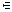
A}.

R =
{(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}.
Reflexive
: As 1 e A and (1, 1)
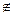
R

R
is not reflexive.
Symmetric
: As 2, 3
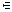
A and (2, 3)
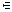
R.
But

R
is not symmetric,
Transitive
: As 2. 3 and 4
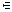
A and (2, 3)
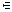
R,
(3, t (2,4)
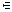
R '

R
is not transitive.
Hence
R is neither reflexive, nor symmetric, nor transitive.
E 4.
Show that the relation R defined
as R = {(a, b) : a 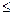 b} is
reflexive and transitive
but not symmetric.
b} is
reflexive and transitive
but not symmetric.
Sol. R
= {(a, b) : a
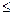
b, a, b
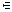
R
}
Reflexive
: As a
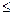
a
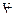
a
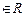
(a,
a)
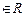
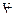
a
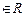
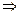
R
is reflexive.
Symmetric
: As 1, 2
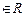
and 1
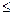
2

(1,
2)
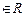
But
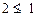

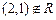
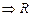
is
not symmetric.
Transitive
: (a, b)
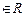
and (b, c)
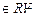
a,
b,c
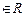
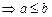
and
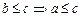
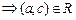

R
is transitive.
Hence
R is reflexive and transitive but not
symmetric.
E5. Check whether the relation R in R defined
by R = {(a, b) : a
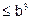
} is
reflexive, symmetric or transitive.
Sol. R = {(a, b) :
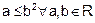
}
Reflexive : as
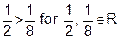
i.e.
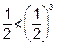
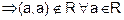
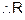
is not
reflexive.
Symmetric : As 1 < 27 for 1, 3
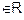
i.e. (1, 3)
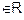
for
1, 3
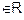
But
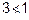
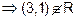
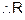
is not
symmetric.
Transitive : As 100 < 125 and 5 <
8
i.e. 100 < 53 and 5 < 23
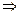
(100, 5)
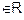
and
(5, 2)
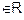
But 100
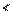
8 i.e. 100
< 23

(100, 2)
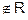

(100, 5)
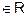
,
(5, 2)
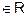
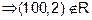

R is not
transitive.
Hence R is neither reflexive nor symmetric nor
transatie.
E6.
Show that the
relation R is the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but
neither reflexive nor transitive.
Sol. Let A = {1, 2, 3} : R = {(1, 2), (2, 1)}
Reflexive : As
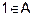
and
(1, 1)
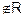
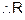
is not
reflexive.
Symmetric : As 1, 2
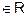
and
(1, 2)
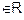
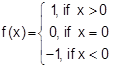 is neither
one-one nor onto.
is neither
one-one nor onto.
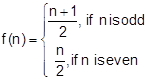 for
all
for
all 
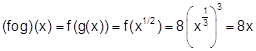 E4.
If
E4.
If 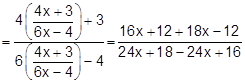
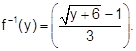 Sol.
Given f(x) = 9x2 + 6x ? 5, Df = R+
Injectivity
: Let x1, x2 be any two elements of R+
such that f(x1) = f(x2)
Sol.
Given f(x) = 9x2 + 6x ? 5, Df = R+
Injectivity
: Let x1, x2 be any two elements of R+
such that f(x1) = f(x2)
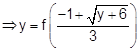
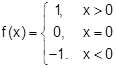 and
g : R
and
g : R 