Relation and Function
Let \[A=\{1,\,2,\,3,4,\}\], \[B=\{2,\,3\}\]
\[A\times B=\{1,\,2,3,\,4,\}\times \{2,3\}=\{(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3)\}\]
Let we choose an arbitrary set:
\[R=[(1,2),(2,2),(1,3),(4,3)]\]
Then R is said to be the relation between a set A to B.
Definition
Relation R is the subset of the Cartesian Product\[A\times B\]. It is represented as \[R=\{(x,y):x\in A\,\] and \[y\in B\}\] {the 2nd element in the ordered pair (x, y) is the image of 1st element}
Sometimes, it is said that a relation on the set A means the all members / elements of the relation
R be the elements / members of \[A\text{ }\times \text{ }A\].
e.g. Let \[A=\{1,\,2,\,3\}\] and a relation R is defined as \[R=\{(x,y):x<y\] where \[x,y\in A\}\]
Sol. \[\because \]\[\mathbf{A=\{1,}\,\mathbf{2,}\,\mathbf{3\}}\]
\[A\times A=\{(1,1),(2,2),(3,3),(2,1),(3,1),(1,2),(3,2),(1,3),(2,3)\}\]
\[\because \,\,\,\,R=\,\,\,\because x<y\]
\[\because \,\,\,\,R=\{(x,y):x<y,and\,x,y\in A\}=\{(1,2),(2,3),(1,3)\]
Note: Let a set A has m elements and set B has n elements. Then \[n(A\times B)\] be \[m\times n\]elements so, total number of relation from A to B or between A and B be\[{{2}^{m\times n}}\].
- A relation can be represented algebraically either by Roster method or set builder method.
Types of Relation
- Void Relation: A relation R from A to B is a null set, then R is said to be void or empty relation.
- Universal Relation: A relation on a set A is said to be universal relation, if each element of A is related to or associated with every element of A.
- Identity Relation: A relation \[{{I}_{x}}\{(x,x):x\in A\}\] on a set A is said to be identity relation on A.
- Reflexive relation: A relation Ron the set A is said to be the reflexive relation. If each and every element of set A is associated to itself. Hence, R is reflexive iff \[(a,\,a)\in R\,\,\forall \,\,a\in A\].
e.g. \[\Rightarrow \,\,A=\{1,\,2,\,3,\,4\}\]
\[R=\{(1,\,3),(1,1),(2,3),(3,2),(2,2),(3,1),(3,3),(4,4)\}\]is a reflexive relation on f.
Sol. Yes, because each and every element of A is related to itself in R.
- Symmetric relation: A relation R on a set A is said to be symmetric relation iff. \[(x,y)\in R\Rightarrow (y,x)\in R\,\,\forall \,\,x,y\in A\]
i.e. \[x\,R\,y\Rightarrow y\,R\,x\,\,\forall \,\,x,y\in A\]
\[\because \] xRy is read as x is R-related to y.
- Anti-symmetric relation: A relation which is not symmetric is said to be anti-symmetric relation.
- Transitive relation: Let A be any non-empty set. A relation R on set A is said to be transitive relation R iff \[(x,y)\in R\] and \[(y,z)\in R\] then \[(x,z)\in R\,\,\forall \,\,x,y,z\in R.\]
i.e. \[xRy\] and \[yRz\Rightarrow xRz\,\,\forall \,\,x,\,y,\,z\in R\].
Let \[\mathbf{A=\{1,}\,\mathbf{2,}\,\mathbf{3,}\,\mathbf{4\}}\]
\[A\times A=\{(1,,1),(2,1),(3,1),(4,1),(1,2),(2,2),(3,2),(4,2),(1,3),(2,3),(3,3),(4,3),(1,4),(2,4),(3,4),(4,4),\]
\[{{R}_{1}}=(1,1),(2,2),(3,2),(2,3),(3,3),(4,4)\]
\[{{R}_{2}}=(2,2),(1,3),(3,3),(3,1),(1,1)\]
\[{{R}_{3}}=(1,1),(2,2),(3,4),(3,3),(4,4)\]
State about\[{{\mathbf{R}}_{\mathbf{1}}}\], \[{{\mathbf{R}}_{\mathbf{2}}}\] and\[{{\mathbf{R}}_{\mathbf{3}}}\]. Are they reflexive, symmetric, anti-symmetric or transitive relations?
Sol. \[{{R}_{1}}\] is symmetric as well as transitive relation for \[{{R}_{2}}\].
\[{{R}_{2}}\]is not reflexive because \[(4,4)\in
more...
e.g. A = {2, 5, 8, 7}
\[2\in A\]. It is read as 2 belongs to set A. Or 2 is the member/element of set A.
\[6\notin A\]- It means 6 doesn't belong to set A. A set is represented by capital letter of English/Greek Alphabet.
\[\alpha ,\beta ,\gamma ,\delta \]or A, B, C, U, S etc.
and its all elements is closed with { } bracket.
Hence what is the difference between 2 and {2}
\[\because \]2 can be element of a set whereas {2} represents a set whose one elements is 2.
Note: A set is the collection of distinguish and distinct things
A set can be written/represented in the two form
(a) Tabular form/Roaster form
(b) Set builder form
e.g.
A triangle has three vertex, three angles and three sides in above figure.
vertex be A, Band C
Angle be \[\angle ABC,\] \[\angle BCA,\] and \[\angle CAB,\]or \[\angle BAC\]
According to sides, type of triangle be
(a) Equilateral Triangle: All sides are equal
(b) Isosceles Triangle: Two sides are equal
(c) Scalene Triangle: All sides are different.
According to Angle, There are three types of triangles:
(a) Acute Angle Triangle
(b) Obtuse Angle Triangle
(c) Right angle Triangle
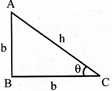Then \[\angle A=90{}^\circ -\theta \]
\[\sin \theta =\frac{P}{h}=\frac{AB}{AC},\,\]\[\cos ec\,\theta =\frac{h}{P}\]
\[\cos \,\theta =\frac{b}{h},\] \[sec\theta =\frac{h}{b}\]
\[\tan \theta =\frac{P}{b},\] \[\cot \theta =\frac{b}{P}\]
Trigonometrical ratio shows the relation between angle and sides of the triangle.
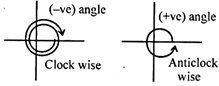
Angle may be positive or negative
When angle be measured in anticlockwise direction then it is positive otherwise negative.
Discontinuous Function
Continuity of a Function at a Point
A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:
(i) f(a) exist. ('a' line in the domain of f)
(ii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L
(iii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)
Continuity from Left and Right
A function f(x) is said to be continuous at a point x = a of its domain if and only if it satisfies the following three condition:
(i) f(a) exist. ('a' line in the domain of f)
(ii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) exist e.e; \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x)= \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(x) or R.H.L= L.H.L
(iii) \[\underset{x+a}{\mathop{\lim }}\,\] f(x) = f(a) (limit equals the value of function)
Cauchy's Definition of Continuity
A function f is said to be continuous at a point a of its domain D if for every \[\varepsilon >o\] there exists \[\delta >o\] (dependent of\[\varepsilon \]) such that \[\left| x-a \right|<\delta \]
\[\Rightarrow \left| \text{f}(x)-\text{f(a)} \right|<\varepsilon \]
Comparing this definition with the definition of limit we find that f(x) is continuous at x = a if \[\underset{x\to a}{\mathop{\lim }}\,\]f(x) exists and is equal to f(a) i.e; \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\] f(a) \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\] f(x).
Continuity from Left and Right
Function f(x) is said to be
(i) Left continuous at x= a if \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]
(ii) Right continuous at x = a if \[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\,\,\text{f(x)=f(a)}\text{.}\]
Thus a function f(x) is continuous at a point x = a if it is left continuous as well as right continuous at x = a.
Differentiation
The function, f(x) is differentiable at point P, iff there exists a unique tangent at point P. In other words, f(x) is differentiable at point P iff the curve does not have pas a corner point i.e; the function is not differentiable at those more... 
Hence, we have
\[\operatorname{Re}(z)=\frac{z+\overline{z}}{2}\] and \[\operatorname{Im}(z)=\frac{z-\overline{z}}{2i}\]
\[\Rightarrow \] Geometrically, the conjugate of z is the reflection or point image of z in the real axis.
e.g.
(i) \[z=3-4i\]
\[z=3-(-4)=3+4i\]
(ii) \[z=2+5i\]
\[\overline{z}=2-5i\]
(iii) \[\overline{z}=5i\]
\[\overline{z}=-5i\]
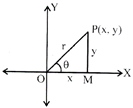Let \[z=x+iy\] is a complex no. It is represented as \[P(x,y).\] more... 
