question_answer 1)
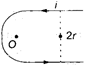
In the figure shown, the magnetic field induction at the point 0 will be
A)
\[\frac{{{\mu }_{0}}i}{2\pi r}\]
done
clear
B)
\[\left( \frac{{{\mu }_{0}}}{4\pi } \right)\left( \frac{i}{r} \right)(\pi +2)\]
done
clear
C)
\[\left( \frac{{{\mu }_{0}}}{4\pi } \right)\left( \frac{i}{r} \right)(\pi +1)\]
done
clear
D)
\[\frac{{{\mu }_{0}}i}{4\pi r}(\pi +1)\]
done
clear
View Answer play_arrow
question_answer 2)
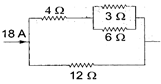
In the electrical network shown in the figure, the potential difference across \[3\,\Omega \] resistance will be
A)
12V
done
clear
B)
2.4V
done
clear
C)
24V
done
clear
D)
36V
done
clear
View Answer play_arrow
question_answer 3)
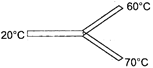
Three identical thermal conductors are connected as shown in figure. Considering no heat loss due to radiation, temperature at the junction will be
A)
\[40{}^\circ C\]
done
clear
B)
\[60{}^\circ C\]
done
clear
C)
\[50{}^\circ C\]
done
clear
D)
\[35{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 4) Surface tension vanishes at
A)
absolute zero temperature
done
clear
B)
transition temperature
done
clear
C)
critical temperature
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 5) A transistor is working in common emitter mode. Its amplification factor (\[\beta \]) is 80. If the base current is 250\[\mu A\], the collector current will be
A)
1.25\[\mu A\]
done
clear
B)
\[\frac{250}{80}\mu A\]
done
clear
C)
430\[\mu A\]
done
clear
D)
\[250\times 80\,\mu A\]
done
clear
View Answer play_arrow
question_answer 6)
From an inclined plane two particles are projected with same speed at same angle \[\theta ,\] one up and other down the plane as shown in figure, which of the following statements is/are correct?
A)
The time of flight of each particle is the same
done
clear
B)
The particles will collide the plane with same speed
done
clear
C)
Both the particles strike the plane perpendicularly
done
clear
D)
The particles will collide in midair if projected simultaneously and time of flight of each parrick is less than the time of collision
done
clear
View Answer play_arrow
question_answer 7)
A battery of emf 10 V is connected to resistance as shown in figure. The potential difference \[{{V}_{A}}-{{V}_{B}}\]between the points A and B is
A)
-2V
done
clear
B)
2V
done
clear
C)
5V
done
clear
D)
\[\frac{20}{11}V\]
done
clear
View Answer play_arrow
question_answer 8) Solar radiation is
A)
transverse electromagnetic wave
done
clear
B)
longitudinal electromagnetic wave
done
clear
C)
stationary wave
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 9) Fundamental frequency of an open pipe is \[{{f}_{0}},\]Fundamental frequency when it is half filled with water is
A)
\[{{f}_{0}}\]
done
clear
B)
\[{{f}_{0}}/2\]
done
clear
C)
\[2{{f}_{0}}\]
done
clear
D)
\[3{{f}_{0}}\]
done
clear
View Answer play_arrow
question_answer 10) If the rms velocity of a gas is v, then
A)
\[{{v}^{2}}T\] = constant
done
clear
B)
\[{{v}^{2}}/T\] = constant
done
clear
C)
\[v{{T}^{2}}\] = constant
done
clear
D)
v is independent of T
done
clear
View Answer play_arrow
question_answer 11) A sounding source of frequency 500 Hz moves towards a stationary observer with a velocity 30 m/s. If the velocity of sound in air is 330 m/s, find the frequency beared by the observer.
A)
500 Hz
done
clear
B)
550 Hz
done
clear
C)
355 Hz
done
clear
D)
55.5 Hz
done
clear
View Answer play_arrow
question_answer 12) At what height h above earth, the value of g becomes g/27 (.R = Radius of earth)
A)
3R
done
clear
B)
\[\sqrt{2}R\]
done
clear
C)
\[(\sqrt{2}-1)R\]
done
clear
D)
\[\frac{1}{\sqrt{2}}R\]
done
clear
View Answer play_arrow
question_answer 13) A freshly prepared radioactive source of half-life 2 h emits radiation of intensity which is 64 times the permissible safe level. Calculate the minimum time after which it would be possible to work safely with this source.
A)
12 h
done
clear
B)
24 h
done
clear
C)
6 h
done
clear
D)
130 h
done
clear
View Answer play_arrow
question_answer 14)
The current in the circuit shown in the figure, considering ideal diode is
A)
20 A
done
clear
B)
\[2\times {{10}^{-3}}A\]
done
clear
C)
200 A
done
clear
D)
\[2\times {{10}^{-4}}A\]
done
clear
View Answer play_arrow
question_answer 15)
The tension in the string in the pulley system shown in the figure is
A)
75 N
done
clear
B)
80 N
done
clear
C)
7.5 N
done
clear
D)
30 N
done
clear
View Answer play_arrow
question_answer 16) A glass flask having mass 390 g and an interior volume of \[500\,c{{m}^{3}}\] floats on water when it is less than half filled with water. The density of material of the flask is
A)
0.8g/cc
done
clear
B)
2.8g/cc
done
clear
C)
1.8g/cc
done
clear
D)
0.28 g/cc
done
clear
View Answer play_arrow
question_answer 17) The angle of minimum deviation \[{{\delta }_{m}}\] for an equilateral glass prism is 30°. Refractive index of the prism is
A)
\[1/\sqrt{2}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
\[2\sqrt{2}\]
done
clear
D)
\[1/2\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 18) When the wavelength of sound changes from 1 m to 1.01 m, the number of beats heard are 4. The velocity of sound is
A)
404 m/s
done
clear
B)
4.04 m/s
done
clear
C)
414 m/s
done
clear
D)
400 m/s
done
clear
View Answer play_arrow
question_answer 19)
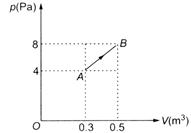
An ideal gas expands along the path AB as shown in the p-V diagram. The work done is
A)
\[4\times {{10}^{4}}J\]
done
clear
B)
\[1.2\times {{10}^{5}}J\]
done
clear
C)
\[2.4\times {{10}^{5}}J\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 20) If force is proportional to square of velocity, then the dimensions of proportionality constant is
A)
\[[M{{L}^{-1}}T]\]
done
clear
B)
\[[M{{L}^{-1}}{{T}^{0}}]\]
done
clear
C)
\[[ML{{T}^{0}}]\]
done
clear
D)
\[[{{M}^{0}}L{{T}^{-1}}]\]
done
clear
View Answer play_arrow
question_answer 21) Two bodies A and B having temperatures \[327{}^\circ C\] and \[427{}^\circ C\] are radiating heat to the surrounding. The surrounding temperature is \[27{}^\circ C\]. The ratio of rates of heat radiation of A to that of B is
A)
0.52
done
clear
B)
0.31
done
clear
C)
0.81
done
clear
D)
0.42
done
clear
View Answer play_arrow
question_answer 22) Two bulbs 40 W and 60 W and rated voltage 240 V are connected in series across a potential difference of 420 V. Which bulb will work at above its rated voltage?
A)
60 W bulb
done
clear
B)
40 W bulb
done
clear
C)
Both will work
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 23) Two cars A and B move along a concentric circular path of radius \[{{r}_{A}}\]and \[{{r}_{B}}\] with velocities \[{{v}_{A}}\]and \[{{v}_{B}}\] maintaining constant distance, then \[\frac{{{v}_{A}}}{{{v}_{B}}}\]is equal to
A)
\[\frac{{{r}_{B}}}{{{r}_{A}}}\]
done
clear
B)
\[\frac{{{r}_{A}}}{{{r}_{B}}}\]
done
clear
C)
\[\frac{r_{A}^{2}}{r_{B}^{2}}\]
done
clear
D)
\[\frac{r_{B}^{2}}{r_{A}^{2}}\]
done
clear
View Answer play_arrow
question_answer 24) A body of mass 10 kg is moving with a constant velocity of 10 m/s. When a constant force acts for 4 s on it, it moves with a velocity 2 m/s in the opposite direction. The acceleration produced in it is
A)
\[3\,m/{{s}^{2}}\]
done
clear
B)
\[-3\,m/{{s}^{2}}\]
done
clear
C)
\[0.3\,m/{{s}^{2}}\]
done
clear
D)
\[0.03\,m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 25) A beam of light is incident at 60° to a plane surface. The reflected and refracted rays are perpendicular to each other than refractive index of the surface is
A)
\[\sqrt{3}\]
done
clear
B)
\[\frac{1}{\sqrt{3}}\]
done
clear
C)
\[\frac{1}{2\sqrt{3}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 26) Two wires of lengths \[l\] and \[2l,\] radii r and 2r respectively having same Youngs modulus are hung with a weight mg. Net elongation is
A)
\[\frac{3mgl}{\pi {{r}^{2}}Y}\]
done
clear
B)
\[\frac{2mgl}{3\pi {{r}^{2}}Y}\]
done
clear
C)
\[\frac{3mgl}{2\pi {{r}^{2}}Y}\]
done
clear
D)
\[\frac{3mgl}{4\pi {{r}^{2}}Y}\]
done
clear
View Answer play_arrow
question_answer 27) A ball rolls off the top of stairway with a horizontal velocity of magnitude 1.8 m/s. The steps are 0.20 m high and 0.20 m wide. Which step will the ball hit first?
A)
First
done
clear
B)
Second
done
clear
C)
Third
done
clear
D)
Fourth
done
clear
View Answer play_arrow
question_answer 28) The peak value of an alternating emf E given by \[E={{E}_{0}}\cos \omega t\] is 10 V and its frequency is 50 Hz. At a time \[t=\frac{1}{600}\]s, the instantaneous value of the emf is
A)
10 V
done
clear
B)
\[5\sqrt{3}v\]
done
clear
C)
5V
done
clear
D)
1V
done
clear
View Answer play_arrow
question_answer 29) A circuit area \[0.01\,{{m}^{2}}\] is kept inside a magnetic field which is normal to its plane. The magnetic field changes from 2 T to 1 T in 1 ms. if the resistance of the circuit is 2\[\Omega \]. The amount of heat evolved is
A)
0.05 J
done
clear
B)
50 J
done
clear
C)
0.50 J
done
clear
D)
500 J
done
clear
View Answer play_arrow
question_answer 30) A convex lens is placed between object and a screen. The size of object is 3 cm and an image of height 9 cm is obtained on the screen. When the lens is displaced to a new position, what will be the size of image on the screen?
A)
2 cm
done
clear
B)
6 cm
done
clear
C)
4 cm
done
clear
D)
1 cm
done
clear
View Answer play_arrow
question_answer 31) A gas is suddenly expanded such that its final volume becomes 3 times its initial volume. If the specific heat at constant volume of the gas is 2R, then the ratio of initial to final pressures is nearly equal to
A)
5
done
clear
B)
6.5
done
clear
C)
7
done
clear
D)
3.5
done
clear
View Answer play_arrow
question_answer 32) Two pendulums have time periods T and 5T/4. They start SHM at the same time from the mean position. What will be the phase difference between them after the bigger pendulum completed one oscillation?
A)
\[45{}^\circ \]
done
clear
B)
\[90{}^\circ \]
done
clear
C)
\[60{}^\circ \]
done
clear
D)
\[30{}^\circ \]
done
clear
View Answer play_arrow
question_answer 33) A body is coming with a velocity of 72 km/h on a rough horizontal surface of coefficient of friction 0.5. If the acceleration due to gravity is \[10\,m/{{s}^{2}},\] find the minimum distance it can be stopped.
A)
400m
done
clear
B)
40m
done
clear
C)
0.40m
done
clear
D)
4m
done
clear
View Answer play_arrow
question_answer 34) A bullet comes out of the barrel of gun of length 2 m with a speed 80 m/s. The average acceleration of the bullet is
A)
\[1.6\,m/{{s}^{2}}\]
done
clear
B)
\[160\,\,m/{{s}^{2}}\]
done
clear
C)
\[1600\,\,m/{{s}^{2}}\]
done
clear
D)
\[16\,\,m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 35) A disc of radius 0.1 m is rotating with a frequency 10 rev/s in a normal magnetic field of strength 0.1 T. Net induced emf is
A)
\[2\pi \times {{10}^{-2}}v\]
done
clear
B)
\[\pi \times {{10}^{-2}}v\]
done
clear
C)
\[\frac{\pi }{2}{{10}^{-2}}V\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 36) 1 \[c{{m}^{3}}\] of water at its boiling point absorbs 540 cal of heat to becomes steam with a volume of 1671 \[c{{m}^{3}}\]. If the atmospheric pressure \[=1.013\times {{10}^{5}}\,N/{{m}^{2}}\]and the mechanical equivalent of heat =4.19 J/cal, the energy spent in this process in overcoming intermolecular forces is
A)
540 cal
done
clear
B)
40 cal
done
clear
C)
500 cal
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 37) A string fixed at both ends oscillaress in 5 segments, length 10 m and velocity of wave is 20 m/s. What is the frequency?
A)
5 Hz
done
clear
B)
15 Hz
done
clear
C)
10 Hz
done
clear
D)
2 Hz
done
clear
View Answer play_arrow
question_answer 38) When the amplitude of a body executing SHM becomes twice what happens?
A)
Maximum potential energy is doubled
done
clear
B)
Maximum kinetic energy is doubled
done
clear
C)
Total energy is doubled
done
clear
D)
Maximum velocity is doubled
done
clear
View Answer play_arrow
question_answer 39) The time period of a geostationary satellite at a height 36000 km is 24 h. A spy satellite orbits earth at a height 6400 km. What will be the time period of spy satellite? [Radius of the earth = 6400 km]
A)
5 h
done
clear
B)
4 h
done
clear
C)
3h
done
clear
D)
12 h
done
clear
View Answer play_arrow
question_answer 40) A bomb of mass 9 kg explodes into two parts. One part of mass 3 kg moves with velocity 16 m/s, then the KE of the other part is
A)
162 J
done
clear
B)
150 J
done
clear
C)
192 J
done
clear
D)
200 J
done
clear
View Answer play_arrow
question_answer 41) In the reaction \[_{7}{{N}^{14}}+\alpha {{\to }_{8}}{{X}^{17}}{{+}_{1}}{{p}^{1}}\] identify X.
A)
\[{{O}_{2}}\]
done
clear
B)
\[{{N}_{2}}\]
done
clear
C)
He
done
clear
D)
Ar
done
clear
View Answer play_arrow
question_answer 42) Current in a coil changes from 5 A to 10 A in 0.2 s. If the coefficient of self-induction is 10 H, then the inducedi emf is
A)
112 V
done
clear
B)
250 V
done
clear
C)
125 V
done
clear
D)
230 V
done
clear
View Answer play_arrow
question_answer 43) The force of interaction between two charges \[{{q}_{1}}=6\mu C\]and \[{{q}_{2}}=2\mu C\] N. If charge \[q=-2\mu C\] is added to each of the charges, then the new force of interaction is
A)
\[2\times {{10}^{-7}}N\]
done
clear
B)
Zero
done
clear
C)
30 N
done
clear
D)
\[2\times {{10}^{-3}}N\]
done
clear
View Answer play_arrow
question_answer 44) The number of turns in primary coil of a transformer is 20 and the number of turns in the secondary is 10. If the voltage across the primary is 220 V, what is the voltage across the secondary?
A)
110 V
done
clear
B)
130 V
done
clear
C)
190 V
done
clear
D)
310 V
done
clear
View Answer play_arrow
question_answer 45)
An electron of an atom transits from\[{{n}_{1}}\], to \[{{n}_{2}}\] . In which of the following, maximum frequency of photon will be emitted?
A)
\[{{n}_{1}}=1\,to\,{{n}_{2}}=2\]
done
clear
B)
\[{{n}_{1}}=2\,\,to\,\,{{n}_{2}}=1\]
done
clear
C)
\[{{n}_{1}}=2\,\,to\,\,{{n}_{2}}=6\]
done
clear
D)
\[{{n}_{1}}=6\,\,to\,\,{{n}_{2}}=2\]
done
clear
View Answer play_arrow
question_answer 46) A rod of length L and mass M is bent to form a semicircular ring as shown in figure. The moment of inertia about XY is
A)
\[\frac{1}{4}\frac{M{{L}^{2}}}{{{\pi }^{2}}}\]
done
clear
B)
\[\frac{2M{{L}^{2}}}{3{{\pi }^{2}}}\]
done
clear
C)
\[\frac{M{{L}^{2}}}{2}\]
done
clear
D)
\[\frac{M{{L}^{2}}}{2}\]
done
clear
View Answer play_arrow
question_answer 47)
In the figure shown, \[{{m}_{1}}=10kg,\,{{m}_{2}}=6\,kg,\] \[{{m}_{4}}=4kg.\,\,\,\]If\[{{T}_{3}}=40N,\,{{T}_{2}}=?.\,\,\,\]
A)
13 N
done
clear
B)
32 N
done
clear
C)
25 N
done
clear
D)
35 N
done
clear
View Answer play_arrow
question_answer 48) A stone is thrown at an angle 9 to be horizontal reaches a maximum height H. Then the time of flight of stone will be
A)
\[\sqrt{\frac{2H}{g}}\]
done
clear
B)
\[2\sqrt{\frac{2H}{g}}\]
done
clear
C)
\[\frac{2\sqrt{2H\,\sin \theta }}{g}\]
done
clear
D)
\[\frac{\sqrt{2H\,\sin \theta }}{g}\]
done
clear
View Answer play_arrow
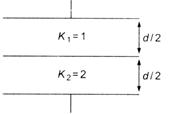
question_answer 49)
Two parallel plates of area A are separated by two different dielectrics as shown in figure. The net capacitance is
A)
\[\frac{{{\varepsilon }_{0}}A}{2d}\]
done
clear
B)
\[\frac{{{\varepsilon }_{0}}A}{d}\]
done
clear
C)
\[\frac{3{{\varepsilon }_{0}}A}{d}\]
done
clear
D)
\[\frac{4{{\varepsilon }_{0}}A}{3d}\]
done
clear
View Answer play_arrow
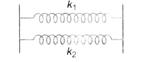
question_answer 50)
Two springs of force constants \[{{k}_{1}}\] and \[{{k}_{2}}\] are connected as shown. The effective spring constant k is
A)
\[{{k}_{1}}+{{k}_{2}}\]
done
clear
B)
\[\frac{{{k}_{1}}}{{{k}_{2}}}\]
done
clear
C)
\[{{k}_{1}}{{k}_{2}}\]
done
clear
D)
\[2{{k}_{1}}{{k}_{2}}\]
done
clear
View Answer play_arrow
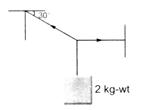
question_answer 51)
A body of weight 2 kg is suspended as shown in figure. The tension \[{{T}_{1}}\] in the horizontal string (in kg-wt) is
A)
\[2/\sqrt{3}\]
done
clear
B)
\[\sqrt{3}/2\]
done
clear
C)
\[2\sqrt{3}\]
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 52) If the momentum of a body is increased by 100%, then the percentage increase in the kinetic energy is
A)
150%
done
clear
B)
200%
done
clear
C)
225%
done
clear
D)
300%
done
clear
View Answer play_arrow
question_answer 53) In Youngs double slit experiment, slit separation is 0.6 mm and the separation between slit and screen is 1.2 m. The angular width is (the wavelength of light used is \[4800\overset{\text{o}}{\mathop{\text{A}}}\,\])
A)
30 rad
done
clear
B)
\[8\times {{10}^{-4}}\] rad
done
clear
C)
12 rad
done
clear
D)
70.5 rad
done
clear
View Answer play_arrow
question_answer 54) X-ray of wavelength \[\lambda =2\overset{0}{\mathop{A}}\,\]is emitted from the metal target. The potential difference applied across the cathode and the metal target is
A)
5525 V
done
clear
B)
320 V
done
clear
C)
6200 V
done
clear
D)
3250 V
done
clear
View Answer play_arrow
question_answer 55) Two identical masses m moving with velocities \[{{u}_{1}}\] and \[{{u}_{2}}\] collide perfectly inefasticatiy. Find the loss in energy.
A)
\[m({{u}_{1}}-u_{2}^{2})\]
done
clear
B)
\[\frac{m}{4}{{({{u}_{1}}-{{u}_{2}})}^{2}}\]
done
clear
C)
\[\frac{m}{2}{{({{u}_{1}}-{{u}_{2}})}^{2}}\]
done
clear
D)
\[m{{({{u}_{1}}-{{u}_{2}})}^{3}}\]
done
clear
View Answer play_arrow
question_answer 56) A constant torque acting on a uniform circular wheel changes its angular momentum from \[{{A}_{0}}\] to \[4{{A}_{0}}\] in 4s. The magnitude of this torque is
A)
\[\frac{3{{A}_{0}}}{4}\]
done
clear
B)
\[{{A}_{0}}\]
done
clear
C)
4\[{{A}_{0}}\]
done
clear
D)
12\[{{A}_{0}}\]
done
clear
View Answer play_arrow
question_answer 57) When a number of small droplets combines to form a large drop, then
A)
energy is absorbed
done
clear
B)
energy is liberated
done
clear
C)
energy is neither liberated nor absorbed
done
clear
D)
process is independent of energy
done
clear
View Answer play_arrow
question_answer 58) With what minimum acceleration can a fireman slide down a rope while breaking strength of the rope is \[\frac{2}{3}\]of the weight?
A)
\[\frac{2}{3}g\]
done
clear
B)
g
done
clear
C)
\[\frac{1}{3}g\]
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 59) If two waves represented by \[{{y}_{1}}=4\sin \,\omega t\] and \[{{y}_{2}}=3\sin \left( \omega t+\frac{\pi }{3} \right)\]interfere at a point. The amplitude of the resulting wave will be about
A)
7
done
clear
B)
6
done
clear
C)
5
done
clear
D)
3.5
done
clear
View Answer play_arrow
question_answer 60) Saturated vapor is compressed to half its volume without any change in temperature, then the pressure will be
A)
doubled
done
clear
B)
halved
done
clear
C)
the same
done
clear
D)
Zero
done
clear
View Answer play_arrow
question_answer 61) The root mean square velocity of a gas is doubled when the temperature is
A)
increased four times
done
clear
B)
increased two times
done
clear
C)
reduced to half
done
clear
D)
reduced to one fourth
done
clear
View Answer play_arrow
question_answer 62) Acidity of phenol is due to
A)
hydrogen bonding
done
clear
B)
phenolic group
done
clear
C)
benzene ring
done
clear
D)
resonance stabilization of its anion
done
clear
View Answer play_arrow
question_answer 63) In which one of the following pairs the radius of the second species is greater than that of the first?
A)
\[Na,\,\,Mg\]
done
clear
B)
\[{{O}^{2-}},\,\,{{N}^{3-}}\]
done
clear
C)
\[L{{i}^{+}},\,\,B{{e}^{2+}}\]
done
clear
D)
\[B{{a}^{2+}},\,\,S{{r}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 64) The radius of the first Bohr orbit of hydrogen atom is\[0.529\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]. The radius of the third orbit of\[{{H}^{+}}\]will be
A)
\[8.46\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[0.705\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[1.59\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[4.79\,\,\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 65) Both\[C{{o}^{3+}}\]and\[P{{t}^{4+}}\]have a coordination number of six. Which of the following pairs of complexes will show approximately the same electrical conductance for their\[~0.001\,\,M\]aqueous solutions?
A)
\[CoC{{l}_{3}}\cdot 4N{{H}_{3}}\]and\[PtC{{l}_{4}}\cdot 4N{{H}_{3}}\]
done
clear
B)
\[CoC{{l}_{3}}\cdot 3N{{H}_{3}}\]and\[PtC{{l}_{4}}\cdot 5N{{H}_{3}}\]
done
clear
C)
\[CoC{{l}_{3}}\cdot 6N{{H}_{3}}\]and\[PtC{{l}_{4}}\cdot 5N{{H}_{3}}\]
done
clear
D)
\[CoC{{l}_{3}}\cdot 6N{{H}_{3}}\]and\[PtC{{l}_{4}}\cdot 3N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 66) When ice melts into water, the entropy
A)
becomes zero
done
clear
B)
remains same
done
clear
C)
decreases
done
clear
D)
increases
done
clear
View Answer play_arrow
question_answer 67) Reduction of nitrobenzene in the presence of\[Zn/N{{H}_{4}}Cl\]gives
A)
azobenzene
done
clear
B)
hydrazobenzene
done
clear
C)
N-phenyl hydroxyl amine
done
clear
D)
aniline
done
clear
View Answer play_arrow
question_answer 68) Which one of the following is not a protein?
A)
Wool
done
clear
B)
Nail
done
clear
C)
Hair
done
clear
D)
DNA
done
clear
View Answer play_arrow
question_answer 69) Which of the following hexoses will form the same osazone when treated with excess phenyl hydrazine?
A)
D-glucose, D-fructose and D-galactose
done
clear
B)
D-glucose, D-fructose and D-mannose
done
clear
C)
D-glucose, D-mannose and D-galactose
done
clear
D)
D-fructose, D-mannose and D-galactose
done
clear
View Answer play_arrow
question_answer 70) A silver cup is plated with silver by passing 965C of electricity. The amount of\[Ag\]deposited is
A)
107.89 g
done
clear
B)
9.89 g
done
clear
C)
1.0002 g
done
clear
D)
1.08 g
done
clear
View Answer play_arrow
question_answer 71) The standard emf of a cell involving one electron change is found to be\[0.591V\]at\[{{25}^{o}}C\]. The equilibrium constant of the reaction is \[(F=96,500\,\,C\,\,mo{{l}^{-1}})\]
A)
\[1.0\times {{10}^{1}}\]
done
clear
B)
\[1.0\times {{10}^{5}}\]
done
clear
C)
\[1.0\times {{10}^{10}}\]
done
clear
D)
\[1.0\times {{10}^{30}}\]
done
clear
View Answer play_arrow
question_answer 72) \[E{}^\circ \]values of\[M{{g}^{2+}}/Mg\]is\[-2.37\,\,V\]of\[Z{{n}^{2+}}/Zn\]is\[-0.76\,\,V\] and\[F{{e}^{2+}}/Fe\]is\[-0.44\,\,V\]. Which of the statements is correct?
A)
\[Zn\]will reduce\[F{{e}^{2+}}\]
done
clear
B)
\[Zn\]will reduce\[M{{g}^{2+}}\]
done
clear
C)
\[Mg\]oxidizes\[Fe\]
done
clear
D)
\[Zn\]oxidizes\[Fe\]
done
clear
View Answer play_arrow
question_answer 73) The maximum proportion of available volume that can be filled by hard spheres in diamond is
A)
0.52
done
clear
B)
0.34
done
clear
C)
0.32
done
clear
D)
0.68
done
clear
View Answer play_arrow
question_answer 74) If we mix a pentavalent impurity in a crystal lattice of germanium, what type of semiconductor formation will occur?
A)
\[p-\]type
done
clear
B)
\[n-\]type
done
clear
C)
Both (a) and (b)
done
clear
D)
None of the two
done
clear
View Answer play_arrow
question_answer 75) Which one of the following complexes is an outer orbital complex? (Atomic numbers\[Mn=25,\,\,Fe=26,\,\,Co=27,\] \[Ni=28\])
A)
\[{{[Fe{{(CN)}_{6}}]}^{4-}}\]
done
clear
B)
\[{{[Mn{{(CN)}_{6}}]}^{4-}}\]
done
clear
C)
\[{{[Co{{(N{{H}_{3}})}_{6}}]}^{3+}}\]
done
clear
D)
\[{{[Ni{{(N{{H}_{3}})}_{6}}]}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 76) The product of reaction between alcoholic silver nitrite with ethyl bromide is
A)
ethene
done
clear
B)
ethane
done
clear
C)
ethyl nitrile
done
clear
D)
nitro ethane
done
clear
View Answer play_arrow
question_answer 77) \[Iso-\]propyl chloride undergoes hydrolysis by
A)
\[{{S}_{N}}1\] mechanism
done
clear
B)
\[{{S}_{N}}2\]mechanisms
done
clear
C)
\[{{S}_{N}}1\]and\[{{S}_{N}}2\]mechanisms
done
clear
D)
Neither\[{{S}_{N}}1\]nor\[{{S}_{N}}2\]mechanism
done
clear
View Answer play_arrow
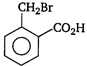
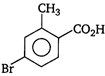
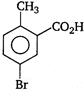
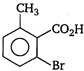
question_answer 78) \[o-\]toluic acid on reaction with\[B{{r}_{2}}+Fe\]gives
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 79)
Consider the acidity of the carboxylic acids I.\[PhCOOH\] II.\[o-N{{O}_{2}}{{C}_{6}}{{H}_{4}}COOH\] III.\[p-N{{O}_{2}}{{C}_{6}}{{H}_{4}}COOH\] IV.\[m-N{{O}_{2}}{{C}_{6}}{{H}_{4}}COOH\]
Which of the following order is correct?
A)
\[I>II>III>IV\]
done
clear
B)
\[II>IV>III>I\]
done
clear
C)
\[II>IV>I>III\]
done
clear
D)
\[II>III>IV>I\]
done
clear
View Answer play_arrow
question_answer 80) Which of the following does not answer iodoform test?
A)
\[n-\]butyl alcohol
done
clear
B)
Acetophenone
done
clear
C)
Acetaldehyde
done
clear
D)
Ethylmethyl ketone
done
clear
View Answer play_arrow
question_answer 81) Which one of the following undergoes reaction with 50% sodium hydroxide solution to give the corresponding alcohol and acid?
A)
Phenol
done
clear
B)
Benzaldehyde
done
clear
C)
Butanal
done
clear
D)
Benzoic acid
done
clear
View Answer play_arrow
question_answer 82) The\[IUPAC\]name of \[C{{H}_{3}}-\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{CH}}\,-CH=\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{C}}\,-CHO\]is
A)
4-hydroxy-1-methylpentanal
done
clear
B)
4-hydroxy-2-methylpent-2-en-1 -al
done
clear
C)
2-hydroxy-4-methylpent-3-en-5 -al
done
clear
D)
2-hydroxy-3-methylpent-2-en-5-al
done
clear
View Answer play_arrow
question_answer 83) The activation energy of exothermic reaction \[A\to B\]is\[80\,\,kJ\,\,mo{{l}^{-1}}\]. The heat of reaction is\[200\,\,kJ\,\,mo{{l}^{-1}}\]. The activation energy for the reaction\[B\to A\]\[(in\,\,kJ\,\,mo{{l}^{-1}})\]will be
A)
80
done
clear
B)
120
done
clear
C)
40
done
clear
D)
280
done
clear
View Answer play_arrow
question_answer 84) Which of the following electrolytes is least effective in coagulating ferric hydroxide solution?
A)
\[KBr\]
done
clear
B)
\[{{K}_{2}}S{{O}_{4}}\]
done
clear
C)
\[{{K}_{2}}Cr{{O}_{4}}\]
done
clear
D)
\[{{K}_{4}}[Fe{{(CN)}_{6}}]\]
done
clear
View Answer play_arrow
question_answer 85) Of the following outer electronic configurations of atoms, the highest oxidation state is achieved by which one of them?
A)
\[(n-1){{d}^{8}},\,\,n{{s}^{2}}\]
done
clear
B)
\[(n-1){{d}^{5}},\,\,n{{s}^{1}}\]
done
clear
C)
\[(n-1){{d}^{3}},\,\,n{{s}^{2}}\]
done
clear
D)
\[(n-1){{d}^{5}},\,\,n{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 86) The relative lowering of vapour pressure of a dilute aqueous solution containing nonvolatile solute is 0.0125. The molality of the solution is about
A)
0.70
done
clear
B)
0.50
done
clear
C)
0.90
done
clear
D)
0.80
done
clear
View Answer play_arrow
question_answer 87) When hydrogen peroxide is added to acidified potassium dichromate, a blue colour is produced due to formation of
A)
\[CrC{{O}_{3}}\]
done
clear
B)
\[C{{r}_{2}}{{O}_{3}}\]
done
clear
C)
\[Cr{{O}_{5}}\]
done
clear
D)
\[CrO_{4}^{2-}\]
done
clear
View Answer play_arrow
question_answer 88) In the following reaction, \[NaOH+S\xrightarrow{{}}A+N{{a}_{2}}S+{{H}_{2}}O;A\]is
A)
\[N{{a}_{2}}S{{O}_{4}}\]
done
clear
B)
\[N{{a}_{2}}S{{O}_{3}}\]
done
clear
C)
\[N{{a}_{2}}S\]
done
clear
D)
\[N{{a}_{2}}{{S}_{2}}{{O}_{3}}\]
done
clear
View Answer play_arrow
question_answer 89) On igniting\[F{{e}_{2}}{{O}_{3}}\]at\[{{1400}^{o}}C\], the product obtained is
A)
\[F{{e}_{2}}{{O}_{3}}\,\,melt\]
done
clear
B)
\[FeO\]
done
clear
C)
\[F{{e}_{3}}{{O}_{4}}\]
done
clear
D)
metallic iron
done
clear
View Answer play_arrow
question_answer 90) Sulphuric acid has great affinity for water because
A)
it hydrolyses the acid
done
clear
B)
it decomposes the acid
done
clear
C)
acid forms hydrates with water
done
clear
D)
acid decomposes water
done
clear
View Answer play_arrow
question_answer 91) Helium-oxygen mixture is used by deep sea divers in preference to nitrogen-oxygen mixture because
A)
helium is much less soluble in blood than nitrogen
done
clear
B)
nitrogen is much less soluble in blood than helium
done
clear
C)
due to high pressure deep under the sea nitrogen and oxygen react to give poisonous nitric oxide
done
clear
D)
nitrogen is highly soluble in water
done
clear
View Answer play_arrow
question_answer 92) One mole of\[C{{O}_{2}}\]contains
A)
\[3\,\,g\]atoms of\[C{{O}_{2}}\]
done
clear
B)
\[18.1\times {{10}^{23}}\]molecules of\[C{{O}_{2}}\]
done
clear
C)
\[6.02\times {{10}^{23}}\]atoms of\[O\]
done
clear
D)
\[6.02\times {{10}^{23}}\]atoms of\[C\]
done
clear
View Answer play_arrow
question_answer 93) The equivalent weight of \[KMn{{O}_{4}}\] for acid solution is
A)
79
done
clear
B)
52.16
done
clear
C)
158
done
clear
D)
31.6
done
clear
View Answer play_arrow
question_answer 94) Which has the highest weight?
A)
\[1\,\,{{m}^{3}}\]of water
done
clear
B)
A normal adult man
done
clear
C)
\[10\,\,L\]of\[Hg\]
done
clear
D)
All have same weight
done
clear
View Answer play_arrow
question_answer 95) Which has the highest\[e/m\]ratio?
A)
\[H{{e}^{2+}}\]
done
clear
B)
\[{{H}^{+}}\]
done
clear
C)
\[H{{e}^{+}}\]
done
clear
D)
\[{{D}^{+}}\]
done
clear
View Answer play_arrow
question_answer 96) The ionization potential order for which set is correct?
A)
\[Cs<Li<K\]
done
clear
B)
\[Cs>Li>B\]
done
clear
C)
\[Li>K>Cs\]
done
clear
D)
\[B>Li<K\]
done
clear
View Answer play_arrow
question_answer 97) The oxidation state of\[Fe\]in\[F{{e}_{3}}{{O}_{4}}\]is
A)
\[+3\]
done
clear
B)
\[8/3\]
done
clear
C)
\[+6\]
done
clear
D)
\[+2\]
done
clear
View Answer play_arrow
question_answer 98) For a first order reaction, the concentration changes from 0.8 to 0.4 in 15 min. The time taken for the concentration to change from \[0.01\,\,M\]to\[0.025\,\,M\] is
A)
30 min
done
clear
B)
15 min
done
clear
C)
7.5 min
done
clear
D)
60 min
done
clear
View Answer play_arrow
question_answer 99) When phenol is treated with excess of bromine water, it gives
A)
\[m-\]bromophenol
done
clear
B)
\[o-\]and prbromophenols
done
clear
C)
\[2,\,\,4-\]dibromophenol
done
clear
D)
\[2,\,\,4,\,\,6-\]tribromophenol
done
clear
View Answer play_arrow
question_answer 100) Which reaction is suitable for the preparation of \[\alpha -\]chloroacetic acid?
A)
Hell-Volhard Zelinsky reaction
done
clear
B)
Nef reaction
done
clear
C)
Stephens reaction
done
clear
D)
Perkin condensation
done
clear
View Answer play_arrow
question_answer 101) Which one of the following compounds will dissolve in an alkali solution after it has undergone reaction with Hinsberg reagent?
A)
\[C{{H}_{3}}N{{H}_{2}}\]
done
clear
B)
\[{{(C{{H}_{3}})}_{3}}N\]
done
clear
C)
\[{{({{C}_{2}}{{H}_{5}})}_{2}}NH\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}NH{{C}_{6}}{{H}_{5}}\]
done
clear
View Answer play_arrow
question_answer 102) Angle strain in cyclopropane is
A)
\[24{}^\circ 44\]
done
clear
B)
\[9{}^\circ 44\]
done
clear
C)
\[44\]
done
clear
D)
\[-5{}^\circ 16\]
done
clear
View Answer play_arrow
question_answer 103) A group of atoms can function as a ligand only when
A)
it is a small molecule
done
clear
B)
it has an unshared electron pair
done
clear
C)
it is a negatively charged ion
done
clear
D)
it is a positively charged ion
done
clear
View Answer play_arrow
question_answer 104) The bond order in\[NO\]is 2.5 while that in\[N{{O}^{+}}\]is 3. Which of the following statements is true for these two species?
A)
Bond length in\[N{{O}^{+}}\]is greater than in\[NO\]
done
clear
B)
Bond length in\[NO\]is greater than In\[N{{O}^{+}}\]
done
clear
C)
Bond length in\[N{{O}^{+}}\]is equal to that in\[NO\]
done
clear
D)
Bond length is unpredictable
done
clear
View Answer play_arrow
question_answer 105) In a homonuclear molecule which of the following set of orbitals is degenerate?
A)
\[\sigma 2s\]and\[\sigma 1s\]
done
clear
B)
\[\pi 2{{p}_{x}}\]and\[\pi 2{{p}_{y}}\]
done
clear
C)
\[\pi 2{{p}_{x}}\]and\[\sigma 2{{p}_{z}}\]
done
clear
D)
\[\sigma 2{{p}_{z}}\]and\[\pi 2{{p}_{x}}\]
done
clear
View Answer play_arrow
question_answer 106) The pH of a neutral water sample is 6.5. Then the temperature of water
A)
is\[{{25}^{o}}C\]
done
clear
B)
is more than\[{{25}^{o}}C\]
done
clear
C)
is less than \[{{25}^{o}}C\]
done
clear
D)
can be more or less than\[{{25}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 107) Which is Lewis acid?
A)
\[B{{F}_{3}}\]
done
clear
B)
\[N{{F}_{3}}\]
done
clear
C)
\[C{{l}^{-}}\]
done
clear
D)
\[{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 108) The\[pH\]of\[{{10}^{-10}}M\,\,NaOH\]solution is nearest to
A)
4
done
clear
B)
-10
done
clear
C)
4
done
clear
D)
7
done
clear
View Answer play_arrow
question_answer 109) Which of the following is not true for carbanions?
A)
The carbon carrying the charge has eight valence electrons
done
clear
B)
They are formed by heterolytic fission
done
clear
C)
They are paramagnetic
done
clear
D)
The carbon carrying the charge is \[s{{p}^{3}}\] hybridized
done
clear
View Answer play_arrow
question_answer 110) Which among the following statements is correct with respect to the optical isomers?
A)
Enantiomers are non-superimposable mirror images
done
clear
B)
Diastereomers are superimposable mirror images
done
clear
C)
Enantiomers are superimposable mirror images
done
clear
D)
Meso forms have no plane of symmetry
done
clear
View Answer play_arrow
question_answer 111) Inductive effect involves
A)
delocalisation of\[\sigma -\]electrons
done
clear
B)
displacement of\[\sigma -\]electrons
done
clear
C)
delocalisation of \[n-\]electrons
done
clear
D)
displacement of\[\pi -\]electrons
done
clear
View Answer play_arrow
question_answer 112) The solubility of\[AgCl\]in\[0.2\,\,M\,\,NaCl\]solution is\[({{K}_{sp}}\,\,of\,\,AgCl=1.20\times {{10}^{-10}})\]
A)
\[6.0\times {{10}^{-10}}M\]
done
clear
B)
\[0.2M\]
done
clear
C)
\[1.2\times {{10}^{-10}}M\]
done
clear
D)
\[0.2\times {{10}^{-10}}M\]
done
clear
View Answer play_arrow
question_answer 113) Lipids are
A)
nucleic acids occurring in plants
done
clear
B)
proteins occurring in animals
done
clear
C)
carbohydrates occurring in plants
done
clear
D)
fats of natural origin
done
clear
View Answer play_arrow
question_answer 114) The enzyme pepsin hydrolyses
A)
proteins to amino acids
done
clear
B)
fats to fatty acids
done
clear
C)
glucose to ethyl alcohol
done
clear
D)
polysaccharides to monosaccharides
done
clear
View Answer play_arrow
question_answer 115) Carboy cannot be used in the reduction of\[A{{l}_{2}}{{O}_{3}}\]because
A)
it is an expensive proposition
done
clear
B)
the enthalpy of formation of\[C{{O}_{2}}\]is more than that of\[A{{l}_{2}}{{O}_{3}}\]
done
clear
C)
pure carbon is not easily available
done
clear
D)
the enthalpy of formation of\[A{{l}_{2}}{{O}_{3}}\]is too high
done
clear
View Answer play_arrow
question_answer 116) Oxalic acid when heated with cone\[{{H}_{2}}S{{O}_{4}}\], gives
A)
\[{{H}_{2}}{{O}_{2}}\]and\[C{{O}_{2}}\]
done
clear
B)
\[CO\]and\[C{{O}_{2}}\]
done
clear
C)
\[{{H}_{2}}{{O}_{2}}\]and\[CO\]
done
clear
D)
\[CaC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 117) At\[{{25}^{o}}C\], the highest osmotic pressure is exhibited by\[0.1\,\,M\]solution of
A)
urea
done
clear
B)
glucose
done
clear
C)
\[KCl\]
done
clear
D)
\[CaC{{l}_{2}}\]
done
clear
View Answer play_arrow
question_answer 118) Ammonia is dried over
A)
slaked lime
done
clear
B)
calcium chloride
done
clear
C)
phosphorus pentoxide
done
clear
D)
quicklime
done
clear
View Answer play_arrow
question_answer 119) \[{{C}_{6}}{{H}_{6}}\xrightarrow[350\,\,K]{{{H}_{2}}S{{O}_{4}}}A\xrightarrow[Fusion]{Alkali}B\xrightarrow[{{H}_{2}}O]{B{{r}_{2}}}C\] In the above sequence, C is
A)
\[o-\]bromophenol
done
clear
B)
\[p-\]bromophenol
done
clear
C)
\[m-\]bromophenol
done
clear
D)
\[2,\,\,4,\,\,6-\]tribromophenol
done
clear
View Answer play_arrow
question_answer 120) Collins reagent is used to convert
A)
\[\rangle C=O\xrightarrow{{}}\rangle CHOH\]
done
clear
B)
\[-C{{H}_{2}}OH\xrightarrow{{}}-CHO\]
done
clear
C)
\[-CHO\xrightarrow{{}}COOH\]
done
clear
D)
\[-CHO\xrightarrow{{}}-C{{H}_{2}}OH\]
done
clear
View Answer play_arrow
question_answer 121) The range of the function\[f(x)={{\log }_{e}}(3{{x}^{2}}-4x+5)\]is
A)
\[\left( -\infty ,\,\,{{\log }_{e}}\frac{11}{3} \right]\]
done
clear
B)
\[\left[ {{\log }_{e}}\frac{11}{3},\,\,\infty \right)\]
done
clear
C)
\[\left[ -{{\log }_{e}}\frac{11}{3},\,\,{{\log }_{e}}\frac{11}{3} \right]\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 122) The domain of the function \[f(x)=\frac{\sqrt{9-{{x}^{2}}}}{{{\sin }^{-1}}(3-x)}\]
A)
\[(2,\,\,3)\]
done
clear
B)
\[[2,\,\,3)\]
done
clear
C)
\[(2,\,\,3]\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 123) The numbers\[a{{}_{n}}s\]are defined by \[{{a}_{0}}=1,\,\,{{a}_{n+1}}=3{{n}^{2}}+n+{{a}_{n}},\,\,(n\ge 0)\] Then,\[{{a}_{n}}\]is equal to
A)
\[{{n}^{3}}+{{n}^{2}}+1\]
done
clear
B)
\[{{n}^{3}}-{{n}^{2}}+1\]
done
clear
C)
\[{{n}^{3}}-{{n}^{2}}\]
done
clear
D)
\[{{n}^{3}}+{{n}^{2}}\]
done
clear
View Answer play_arrow
question_answer 124) Nishi has 5 coins each of the different denomination. The number different sums of money she conform
A)
32
done
clear
B)
25
done
clear
C)
31
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 125) There are P copies of n-different books. The number of different ways in which a non-empty selection can be made from them, is
A)
\[{{(P+1)}^{n}}-1\]
done
clear
B)
\[{{P}^{n}}-1\]
done
clear
C)
\[{{(P+1)}^{n-1}}-1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 126) Out of 18 points in a plane no three are in the same straight line except five points which are collinear. The number of straight lines that can be formed joining them, is
A)
143
done
clear
B)
144
done
clear
C)
153
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 127) The term independent of\[x\]in \[{{\left[ \sqrt{\left( \frac{x}{3} \right)+}\sqrt{\left( \frac{3}{2{{x}^{2}}} \right)} \right]}^{10}}\]
A)
\[1\]
done
clear
B)
\[^{10}{{C}_{1}}\]
done
clear
C)
\[\frac{5}{12}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 128) The greatest coefficient in the expansion of \[{{(1+x)}^{2n}}\] is
A)
\[^{2n}{{C}_{n}}\]
done
clear
B)
\[^{2n}{{C}_{n-1}}\]
done
clear
C)
\[^{2n}{{C}_{n-2}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 129) The number of terms in the expansion of\[{{(\sqrt{5}+\sqrt[4]{11})}^{124}}\]which are integers, is equal to
A)
0
done
clear
B)
30
done
clear
C)
31
done
clear
D)
32
done
clear
View Answer play_arrow
question_answer 130) The constant term in the expansion of\[{{(1+x)}^{m}}{{\left( 1+\frac{1}{x} \right)}^{n}}\]
A)
\[^{m+n}{{C}_{m-1}}\]
done
clear
B)
\[^{m+n}{{C}_{n}}\]
done
clear
C)
\[^{m+n}{{C}_{m-n}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 131) If\[a>1\], roots of the equation\[(1-a){{x}^{2}}+3ax-1=0\]are
A)
one positive and one negative
done
clear
B)
both negative
done
clear
C)
both positive
done
clear
D)
both non-real complex
done
clear
View Answer play_arrow
question_answer 132) The number of values of the triplet\[(a,\,\,b,\,\,c)\]for which\[a\cos 2x+b{{\sin }^{2}}x+c=0\]is satisfied by all real\[x\], is
A)
0
done
clear
B)
2
done
clear
C)
3
done
clear
D)
infinite
done
clear
View Answer play_arrow
question_answer 133) If\[\alpha ,\,\,\beta ,\,\,\gamma \]are such that\[\alpha +\beta +\gamma =2,\]\[{{\alpha }^{2}}+{{\beta }^{2}}+{{\gamma }^{2}}=6\],\[{{\alpha }^{3}}+{{\beta }^{3}}+{{\gamma }^{3}}=8\], then\[{{\alpha }^{4}}+{{\beta }^{4}}+{{\gamma }^{4}}\]is
A)
5
done
clear
B)
18
done
clear
C)
12
done
clear
D)
36
done
clear
View Answer play_arrow
question_answer 134) If\[a,\,\,b,\,\,c\]are three distinct positive real numbers of real roots of\[a{{x}^{2}}+2b|x|-c=0\]is
A)
4
done
clear
B)
2
done
clear
C)
0
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 135) If\[A\]is a skew-symmetric matrix, then trace of\[A\]is
A)
1
done
clear
B)
-1
done
clear
C)
0
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 136) If the matrix\[A=\left[ \begin{matrix} y+a & b & c \\ a & y+b & c \\ a & b & y+c \\ \end{matrix} \right]\]has rank 3, then
A)
\[y\ne (a-b+c)\]
done
clear
B)
\[y\ne 1\]
done
clear
C)
\[y=0\]
done
clear
D)
\[y\ne -(a+b+c)\]and\[y\ne 0\]
done
clear
View Answer play_arrow
question_answer 137) For positive numbers\[x,\,\,y,\,\,z\]the numerical value of the determinant \[\left| \begin{matrix} 1 & {{\log }_{x}}y & {{\log }_{x}}z \\ {{\log }_{y}}x & 1 & {{\log }_{y}}z \\ {{\log }_{z}}x & {{\log }_{z}}y & 1 \\ \end{matrix} \right|\]
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 138) If\[A\]is an orthogonal matrix, then
A)
\[\det \,\,A=not\,\,exist\]
done
clear
B)
\[\det \,\,A=0\]
done
clear
C)
\[\det \,\,A=\pm 1\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 139) Let\[a,\,\,b,\,\,c\]be real numbers with\[a\ne 0\]and let \[\alpha ,\,\,\beta \]be the roots of the equation\[a{{x}^{2}}+bx+c=0\], then\[{{a}^{3}}{{x}^{2}}+abcx+{{c}^{3}}=0\]has roots
A)
\[{{\alpha }^{2}}\beta ,{{\beta }^{2}}\alpha \]
done
clear
B)
\[\alpha ,{{\beta }^{2}}\]
done
clear
C)
\[{{\alpha }^{2}}\beta ,\beta \alpha \]
done
clear
D)
\[{{\alpha }^{3}}\beta ,{{\beta }^{3}}\alpha \]
done
clear
View Answer play_arrow
question_answer 140) If\[{{n}_{1}},\,\,{{n}_{2}}\]are positive integers, then\[{{(1+i)}^{{{n}_{1}}}}+{{(1+{{i}^{3}})}^{{{n}_{1}}}}+{{(1+{{i}^{5}})}^{{{n}_{2}}}}+{{(1+{{i}^{7}})}^{{{n}_{2}}}}\]is a real number if and only if
A)
\[{{n}_{1}}={{n}_{2}}+1\]
done
clear
B)
\[{{n}_{1}}={{n}_{2}}\]
done
clear
C)
\[{{n}_{1}},\,\,{{n}_{2}}\]are any two negative integers
done
clear
D)
\[{{n}_{1}},\,\,{{n}_{2}}\]are both any positive integers
done
clear
View Answer play_arrow
question_answer 141) The equation\[|z+i|-|z-i|\,\,=k\]represent a hyperbola, if
A)
\[-2<k<2\]
done
clear
B)
\[k>2\]
done
clear
C)
\[0<k<2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 142) The period of the function\[f(x)=|\sin 4x|+|\cos 4x|\]is
A)
\[\pi /2\]
done
clear
B)
\[\pi /8\]
done
clear
C)
\[\pi /4\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 143) If\[\cos x=\frac{2\cos y-1}{2-\cos y}\], where\[x,\,\,y\in (0,\,\,\pi )\], then\[\tan \frac{x}{2}\cdot \cot \frac{y}{2}\]is equal to
A)
\[\sqrt{2}\]
done
clear
B)
\[\sqrt{3}\]
done
clear
C)
\[\frac{1}{\sqrt{2}}\]
done
clear
D)
\[\frac{1}{\sqrt{3}}\]
done
clear
View Answer play_arrow
question_answer 144) The value of\[\cos \frac{2\pi }{15}\cdot \cos \frac{4\pi }{15}\cdot \cos \frac{8}{15}\cdot \cos \frac{16\pi }{15}\]is equal to
A)
\[\frac{1}{16}\]
done
clear
B)
\[\frac{1}{32}\]
done
clear
C)
\[\frac{1}{64}\]
done
clear
D)
\[\frac{1}{8}\]
done
clear
View Answer play_arrow
question_answer 145) The sum of all the solutions of the equation\[\cos x\cdot \cos \left( \frac{\pi }{3}+x \right)\cdot \cos \left( \frac{\pi }{3}-x \right)=\frac{1}{4}\],\[x\in [0,\,\,6\pi ]\]is
A)
\[15\pi \]
done
clear
B)
\[30\pi \]
done
clear
C)
\[\frac{110\pi }{3}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 146) \[2{{\tan }^{-1}}(\cos ec{{\tan }^{-1}}x-\tan \,\,{{\cot }^{-1}}x)\]is equal to
A)
\[{{\cot }^{-1}}x\]
done
clear
B)
\[{{\cot }^{-1}}\frac{1}{x}\]
done
clear
C)
\[{{\tan }^{-1}}x\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 147) The value of\[{{\sin }^{-1}}\left[ \cos \left( {{\sin }^{-1}}\sqrt{\frac{2-\sqrt{3}}{4}} \right. \right.\]\[\left. \left. +{{\cos }^{-1}}\frac{\sqrt{12}}{4}+{{\sec }^{-1}}\sqrt{2} \right) \right]\]is
A)
0
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{6}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 148) In a\[\Delta \,\,ABC,\,\,\angle B={{90}^{o}}\],then\[{{\tan }^{2}}\left( \frac{A}{2} \right)\]is
A)
\[\frac{b-c}{b+c}\]
done
clear
B)
\[\frac{b+c}{b-c}\]
done
clear
C)
\[\frac{b-2c}{b+c}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 149) In a triangle, if\[{{r}_{1}}>{{r}_{2}}>{{r}_{3}}\], then
A)
\[a>b>c\]
done
clear
B)
\[a<b<c\]
done
clear
C)
\[a>b\]and\[b<c\]
done
clear
D)
\[a<b\]and\[b>c\]
done
clear
View Answer play_arrow
question_answer 150) A and B are two points on one bank of a straight river and C, D are two other points on the other bank of river, if direction from A to B is same as that from C to D and\[AB=a\],\[\angle CAD=\alpha \],\[\angle DAB=\beta \],\[\angle CBA=\gamma \], then CD is equal to
A)
\[\frac{a\sin \beta \cdot \sin \gamma }{\sin \alpha \cdot \sin (\alpha +\beta +\gamma )}\]
done
clear
B)
\[\frac{a\sin \alpha \cdot \sin \gamma }{\sin \beta \cdot \sin (\alpha +\beta +\gamma )}\]
done
clear
C)
\[\frac{a\sin \alpha \cdot \sin \beta }{\sin \gamma \cdot \sin (\alpha +\beta +\gamma )}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 151) In a trapezoid of the vector\[\overset{\to }{\mathop{\mathbf{BC}}}\,=\lambda \overset{\to }{\mathop{\mathbf{AD}}}\,\]. We will, then find that\[\overset{\to }{\mathop{\mathbf{P}}}\,=\overset{\to }{\mathop{\mathbf{AC}}}\,+\overset{\to }{\mathop{\mathbf{BD}}}\,\]is collinear with\[\overset{\to }{\mathop{\mathbf{AD}}}\,\]. If\[\overset{\to }{\mathop{\mathbf{P}}}\,=\mu \overset{\to }{\mathop{\mathbf{AD}}}\,\], then
A)
\[\mu =\lambda +1\]
done
clear
B)
\[\lambda =\mu +1\]
done
clear
C)
\[\lambda +\mu =1\]
done
clear
D)
\[\mu =2+\lambda \]
done
clear
View Answer play_arrow
question_answer 152) If\[P(\overrightarrow{\mathbf{p}}),\text{ }Q(\overrightarrow{\mathbf{q}}),\text{ }R(\overrightarrow{\mathbf{r}})\]and\[S(\overrightarrow{\mathbf{s}})\]be four points such that\[3\overrightarrow{\mathbf{p}}+8\overrightarrow{\mathbf{q}}=6\overrightarrow{\mathbf{r}}+5\overrightarrow{\mathbf{s}}\], then the lines\[PQ\] and\[RS\]are
A)
skew
done
clear
B)
intersecting
done
clear
C)
parallel
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 153) Let\[\overrightarrow{\mathbf{a}}=2\widehat{\mathbf{i}}+\widehat{\mathbf{j}}-2\widehat{\mathbf{k}}\]and\[\overrightarrow{\mathbf{b}}=\mathbf{\hat{i}}+\widehat{\mathbf{j}}\], if\[\overrightarrow{\mathbf{c}}\]is a vector such that\[\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{c}}=|\overrightarrow{\mathbf{c}}|,\,\,|\overrightarrow{\mathbf{c}}-\overrightarrow{\mathbf{a}}|=2\sqrt{2}\]and the angle between\[\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}}\]and\[\overrightarrow{\mathbf{c}}\]is\[{{30}^{o}}\], then\[|(\overrightarrow{\mathbf{a}}\times \overrightarrow{\mathbf{b}})\times \overrightarrow{\mathbf{c}}|\]is equal to
A)
\[\frac{2}{3}\]
done
clear
B)
\[\frac{3}{2}\]
done
clear
C)
\[2\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 154) Consider a tetrahedron with faces\[{{F}_{1}},\,\,{{F}_{2}},\,\,{{F}_{3}},\,\,{{F}_{4}}\]. Let\[{{V}_{1}},\,\,{{V}_{2}},\,\,{{V}_{3}},\,\,{{V}_{4}}\]be the vectors whose magnitudes are respectively equal to areas of\[{{F}_{1}},\,\,{{F}_{2}},\,\,{{F}_{3}},\,\,{{F}_{4}}\] and whose directions are perpendicular to these faces in outward direction, then\[|{{\overset{\to }{\mathop{\mathbf{V}}}\,}_{\mathbf{1}}}\mathbf{+}{{\overset{\to }{\mathop{\mathbf{V}}}\,}_{\mathbf{2}}}\mathbf{+}{{\overset{\to }{\mathop{\mathbf{V}}}\,}_{\mathbf{3}}}\mathbf{+}{{\overset{\to }{\mathop{\mathbf{V}}}\,}_{\mathbf{4}}}|\]equals
A)
1
done
clear
B)
4
done
clear
C)
\[\vec{0}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 155) If\[V\]is the volume of the parallelepiped having three coterminus edges as\[\overrightarrow{\mathbf{a}},\,\,\overrightarrow{\mathbf{b}}\]and\[\overrightarrow{\mathbf{c}}\], then the volume of the parallelepiped having three coterminus edge as \[\overrightarrow{\alpha }=(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{a}})\overrightarrow{\mathbf{a}}+(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}})\overrightarrow{\mathbf{b}}+(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{c}})\overrightarrow{\mathbf{c}}\], \[\overrightarrow{\beta }=(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{b}})\overrightarrow{\mathbf{a}}+(\overrightarrow{\mathbf{b}}\cdot \overrightarrow{\mathbf{b}})\overrightarrow{\mathbf{b}}+(\overrightarrow{\mathbf{b}}\cdot \overrightarrow{\mathbf{c}})\overrightarrow{\mathbf{c}}\] \[\overrightarrow{\gamma }=(\overrightarrow{\mathbf{a}}\cdot \overrightarrow{\mathbf{c}})\overrightarrow{\mathbf{a}}+(\overrightarrow{\mathbf{b}}\cdot \overrightarrow{\mathbf{c}})\overrightarrow{\mathbf{b}}+(\overrightarrow{\mathbf{c}}\cdot \overrightarrow{\mathbf{c}})\overrightarrow{\mathbf{c}}\]
A)
\[{{V}^{3}}\]
done
clear
B)
\[3V\]
done
clear
C)
\[{{V}^{2}}\]
done
clear
D)
\[2V\]
done
clear
View Answer play_arrow
question_answer 156) Let us define the length of a vector\[a\widehat{\mathbf{i}}+b\widehat{\mathbf{j}}+c\widehat{\mathbf{k}}\]as\[|a|+|b|+|c|\]. This definition coincides with the usual definition of length of a vector\[a\widehat{\mathbf{i}}+b\widehat{\mathbf{j}}+c\widehat{\mathbf{k}}\], if
A)
\[a=b=c=0\]
done
clear
B)
any two of\[a,\,\,b\]and\[c\]are zero
done
clear
C)
any one of\[a,\,\,b\]and\[c\]is zero
done
clear
D)
\[a+b+c=0\]
done
clear
View Answer play_arrow
question_answer 157) Let\[\overrightarrow{\mathbf{u}}=\widehat{\mathbf{i}}+\widehat{\mathbf{j}}\],\[\overrightarrow{\mathbf{v}}=\widehat{\mathbf{i}}-\widehat{\mathbf{j}}\]and\[\overset{\to }{\mathop{\mathbf{w}}}\,=\widehat{\mathbf{i}}+2\widehat{\mathbf{j}}+3\widehat{\mathbf{k}}\], if\[\widehat{\mathbf{n}}\]is a unit vector such that\[\mathbf{\vec{u}}\cdot \widehat{\mathbf{n}}=0\]and \[\overrightarrow{\mathbf{v}}\cdot \widehat{\mathbf{n}}=0\], then\[|\overset{\to }{\mathop{\mathbf{w}}}\,.\widehat{\mathbf{n}}|\]is equal to
A)
3
done
clear
B)
0
done
clear
C)
1
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 158) For two events A and B, it is given that\[P(A)=P\left( \frac{A}{B} \right)=\frac{1}{4}\]and\[P\left( \frac{B}{A} \right)=\frac{1}{2}\]. Then
A)
A and B are mutually exclusive events
done
clear
B)
A and B are dependent events
done
clear
C)
\[P\left( \frac{A}{B} \right)=\frac{3}{4}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 159) The least number of times a fair coin must be tossed so that the probability of getting at least one head is at least 0.8 is
A)
7
done
clear
B)
6
done
clear
C)
5
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 160) If\[x\]follows a binomial distribution with parameters\[n=100\]and\[p=\frac{1}{3}\], then\[p(X=r)\]is maximum when r equals
A)
16
done
clear
B)
32
done
clear
C)
33
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 161) If\[{{\bar{x}}_{1}}\]and\[{{\bar{x}}_{2}}\]are the means of two distributions such that\[{{\bar{x}}_{1}}<{{\bar{x}}_{2}}\]and\[\bar{x}\]is the mean of the combined distribution, then
A)
\[\bar{x}<{{\bar{x}}_{1}}\]
done
clear
B)
\[\bar{x}>{{\bar{x}}_{2}}\]
done
clear
C)
\[\bar{x}=\frac{{{{\bar{x}}}_{1}}+{{{\bar{x}}}_{2}}}{2}\]
done
clear
D)
\[{{\bar{x}}_{1}}<\bar{x}<{{\bar{x}}_{2}}\]
done
clear
View Answer play_arrow
question_answer 162) If the axes be turned through an angle\[{{\tan }^{-1}}2\]. What does the equation\[4xy-3{{x}^{2}}={{a}^{2}}\]become?
A)
\[{{X}^{2}}-4{{Y}^{2}}={{a}^{2}}\]
done
clear
B)
\[{{X}^{2}}+4{{Y}^{2}}={{a}^{2}}\]
done
clear
C)
\[{{X}^{2}}+4{{Y}^{2}}=-{{a}^{2}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 163) If\[{{t}_{1}},\,\,{{t}_{2}}\]and\[{{t}_{3}}\]are distinct, the points\[({{t}_{1}},\,\,2a{{t}_{1}},\,\,at_{1}^{3})\],\[({{t}_{2}},\,\,2a{{t}_{2}},\,\,at_{2}^{3})\]\[({{t}_{3}},\,\,2a{{t}_{3}},\,\,at_{3}^{3})\]are collinear, if
A)
\[{{t}_{1}}{{t}_{2}}{{t}_{3}}=1\]
done
clear
B)
\[{{t}_{1}}+{{t}_{2}}+{{t}_{3}}={{t}_{1}}{{t}_{2}}{{t}_{3}}\]
done
clear
C)
\[{{t}_{1}}+{{t}_{2}}+{{t}_{3}}=0\]
done
clear
D)
\[{{t}_{1}}+{{t}_{2}}+{{t}_{3}}=-1\]
done
clear
View Answer play_arrow
question_answer 164) The distance of the point (2, 3) from the line \[2x-3y+9=0\]measured along a line\[x-y+1=0\]is
A)
\[4\sqrt{2}\]
done
clear
B)
\[2\sqrt{2}\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[\frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 165) The equation of the straight line which passes through the intersection of the lines\[x-y-1=0\]and\[2x-3y+1=0\]and is parallel to x-axis, is
A)
\[y=3\]
done
clear
B)
\[y=-3\]
done
clear
C)
\[x+y=3\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 166) If the straight line\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\],\[{{a}_{1}}x+{{b}_{1}}y+{{c}_{2}}=0\], \[{{a}_{2}}x+{{b}_{2}}y+{{d}_{1}}=0\]and\[{{a}_{2}}x+{{b}_{2}}y+{{d}_{2}}=0\]are the sides of rhombus, then
A)
\[(a_{2}^{2}+b_{2}^{2}){{({{c}_{1}}-{{c}_{2}})}^{2}}=(a_{1}^{2}+b_{1}^{2}){{({{d}_{1}}-{{d}_{2}})}^{2}}\]
done
clear
B)
\[(a_{1}^{2}+b_{1}^{2})|{{d}_{1}}-{{d}_{2}}|\,\,=(a_{2}^{2}+b_{2}^{2})|{{c}_{1}}-{{c}_{2}}|\]
done
clear
C)
\[(a_{2}^{2}+b_{2}^{2}){{({{d}_{1}}-{{d}_{2}})}^{2}}=(a_{1}^{2}+b_{1}^{2}){{({{c}_{1}}-{{c}_{2}})}^{2}}\]
done
clear
D)
\[(a_{1}^{2}+b_{1}^{2})|{{c}_{1}}-{{c}_{2}}|\,\,=(a_{2}^{2}+b_{2}^{2})|{{d}_{1}}-{{d}_{2}}\]
done
clear
View Answer play_arrow
question_answer 167) The equation\[3{{x}^{2}}+7xy+2{{y}^{2}}+5x+5y+2=0\] represents
A)
a pair of straight lines
done
clear
B)
a circle
done
clear
C)
an ellipse
done
clear
D)
a hyperbola
done
clear
View Answer play_arrow
question_answer 168) To the lines\[a{{x}^{2}}+2hxy+b{{y}^{2}}=0\]the lines \[{{a}^{2}}{{x}^{2}}+2h(a+b)xy+{{b}^{2}}{{y}^{2}}=0\], are
A)
equally inclined
done
clear
B)
perpendicular
done
clear
C)
bisector of the angle
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 169) Consider four circles\[{{(x\pm 1)}^{2}}+{{(y\pm 1)}^{2}}=1\], then the equation of smaller circle touching these four circle is
A)
\[{{x}^{2}}+{{y}^{2}}=3-\sqrt{2}\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}=6-3\sqrt{2}\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}=5-2\sqrt{2}\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}=3-2\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 170) The locus of the point of intersection of tangents to the circle\[x=a\cos \theta ,\,\,y=a\sin \theta \]at the points, whose parametric angles differe by\[\frac{\pi }{2}\], is
A)
a straight line
done
clear
B)
a circle
done
clear
C)
a pair of straight line
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 171) The equation of the circle passing through (1, 0) and (0, 1) and having the smallest possible radius is
A)
\[{{x}^{2}}-{{y}^{2}}-x-y=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-x-y=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+x+y=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-2x-2y=0\]
done
clear
View Answer play_arrow
question_answer 172) The length of the common chord of the two circles\[{{(x-a)}^{2}}+{{(y-b)}^{2}}={{c}^{2}}\]and\[{{(x-b)}^{2}}+{{(y-a)}^{2}}={{c}^{2}}\]
A)
\[\sqrt{4{{c}^{2}}+2{{(a-b)}^{2}}}\]
done
clear
B)
\[\sqrt{4{{c}^{2}}-{{(a-b)}^{2}}}\]
done
clear
C)
\[\sqrt{4{{c}^{2}}-2{{(a-b)}^{2}}}\]
done
clear
D)
\[\sqrt{2{{c}^{2}}-2{{(a-b)}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 173) If\[\left( {{m}_{i}},\,\,\frac{1}{{{m}_{i}}} \right)\]are four distinct points on a circle, then
A)
\[{{m}_{1}}{{m}_{2}}{{m}_{3}}{{m}_{4}}=1\]
done
clear
B)
\[{{m}_{1}}{{m}_{2}}{{m}_{3}}{{m}_{4}}=-1\]
done
clear
C)
\[{{m}_{1}}{{m}_{2}}{{m}_{3}}{{m}_{4}}=\frac{1}{2}\]
done
clear
D)
\[\frac{1}{{{m}_{1}}}+\frac{1}{{{m}_{2}}}+\frac{1}{{{m}_{3}}}+\frac{1}{{{m}_{4}}}\]
done
clear
View Answer play_arrow
question_answer 174) If the normal to the parabola\[{{y}^{2}}=4ax\]at the point\[(a{{t}^{2}},\,\,2aT)\]cuts the parabola again at
A)
\[-2\le T\le 2\]
done
clear
B)
\[T\in (-\infty ,\,\,-8)\cup (8,\,\,\infty )\]
done
clear
C)
\[{{T}^{2}}<8\]
done
clear
D)
\[{{T}^{2}}\ge 8\]
done
clear
View Answer play_arrow
question_answer 175) The number of real tangents that can be drawn to the ellipse\[3{{x}^{2}}+5{{y}^{2}}=32\]passing through (3, 5) is
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
infinite
done
clear
View Answer play_arrow
question_answer 176) If the equation \[l{{x}^{2}}+2mxy+n{{y}^{2}}=0\]represents a pair conjugate diameter of the hyperbola\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\], then
A)
\[l{{a}^{2}}+n{{b}^{2}}=0\]
done
clear
B)
\[l{{a}^{2}}=n{{b}^{2}}\]
done
clear
C)
\[2l{{a}^{2}}=n{{b}^{2}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 177) If\[e\]is the eccentricity of the hyperbola\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\]and\[\theta \]is the angle between the asymptotes, then\[\cos \left( \frac{\theta }{2} \right)\]is equal to
A)
\[\frac{1}{e}\]
done
clear
B)
\[\frac{-1}{e}\]
done
clear
C)
\[e\]
done
clear
D)
\[\frac{2}{e}\]
done
clear
View Answer play_arrow
question_answer 178) The tangent and normal to a rectangular hyperbola\[xy={{c}^{2}}\]at a point cuts off intercepts\[{{a}_{1}}\]and\[{{a}_{2}}\]on one axis and\[{{b}_{1}},\,\,{{b}_{2}}\]on the other, then\[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}\]is equal to
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 179) The direction cosines of any normal to the\[xy-\]plane are
A)
1, 0, 0
done
clear
B)
0, 1, 0
done
clear
C)
1, 1, 0
done
clear
D)
0, 0, 1
done
clear
View Answer play_arrow
question_answer 180) The locus of the equation\[xy+yz=0\]is
A)
a pair of straight lines
done
clear
B)
a pair of parallel lines
done
clear
C)
a pair of perpendicular planes
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 181) The reflection of the point (2, -1, 3) in the plane\[3x-2y-z=9\]is
A)
\[\left( \frac{26}{7},\,\,\frac{15}{7},\,\,\frac{17}{7} \right)\]
done
clear
B)
\[\left( \frac{26}{7},\,\,\frac{-15}{7},\,\,\frac{17}{7} \right)\]
done
clear
C)
\[\left( \frac{15}{7},\,\,\frac{26}{7},\,\,\frac{-17}{7} \right)\]
done
clear
D)
\[\left( \frac{26}{7},\,\,\frac{17}{7},\,\,\frac{-15}{7} \right)\]
done
clear
View Answer play_arrow
question_answer 182) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{1-\cos 2x}}{\sqrt{2}\cdot x}\]is
A)
1
done
clear
B)
-1
done
clear
C)
zero
done
clear
D)
does not exist
done
clear
View Answer play_arrow
question_answer 183) If\[f(x)\left\{ \begin{matrix} a{{x}^{2}}+b, & 0\le x\le 1 \\ x+3, & 1<x\le 2 \\ 4, & x=1 \\ \end{matrix} \right.\], then the value of \[(a,\,\,b)\]for which\[f(x)\]cannot be continuous at\[x=1\]is
A)
(2, 2)
done
clear
B)
(3, 1)
done
clear
C)
(4, 0)
done
clear
D)
(5, 2)
done
clear
View Answer play_arrow
question_answer 184) If\[f(x)={{\log }_{x}}(\log x)\], then\[f(x)\]at\[x=e\]is
A)
\[1/e\]
done
clear
B)
\[e\]
done
clear
C)
\[-1/e\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 185) Radius of the circle \[\overset{\to }{\mathop{{{\mathbf{r}}^{\mathbf{2}}}}}\,+\overrightarrow{\mathbf{r}}(2\widehat{\mathbf{i}}-\widehat{\mathbf{j}}-4\widehat{\mathbf{k}})-19=0\] \[\overrightarrow{\mathbf{r}}\cdot (\widehat{\mathbf{i}}-2\widehat{\mathbf{j}}+2\widehat{\mathbf{k}})+8=0\], is
A)
5
done
clear
B)
4
done
clear
C)
3
done
clear
D)
2
done
clear
View Answer play_arrow
question_answer 186) If\[{{x}^{y}}={{e}^{x}}^{-y}\], then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{\log x}{{{(1+\log x)}^{2}}}\]
done
clear
B)
\[\frac{x-y}{(1+\log x)}\]
done
clear
C)
\[\frac{x-y}{{{(1+\log x)}^{2}}}\]
done
clear
D)
\[\frac{1}{(1+\log x)}\]
done
clear
View Answer play_arrow
question_answer 187) If\[y=\sin (m{{\sin }^{-1}}x)\], then\[(1-{{x}^{2}})y-xy\]is equal to
A)
\[{{m}^{2}}y\]
done
clear
B)
\[my\]
done
clear
C)
\[-{{m}^{2}}y\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 188) If\[f(x)=(ax+b)\sin x+(cx+d)\cos x\], then the values of\[a,\,\,b,\,\,c\]and\[d\]such that\[f(x)=x\cos x\]for all\[x\], are
A)
\[b=c=0,\,\,a=d=1\]
done
clear
B)
\[b=d=0,\,\,a=c=1\]
done
clear
C)
\[c=d=0,\,\,a=b=1\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 189) If a particle is moving such that the velocity acquired is proportional to the square root of the distance covered, then its acceleration is
A)
a constant
done
clear
B)
\[\propto {{s}^{2}}\]
done
clear
C)
\[\propto \frac{1}{{{s}^{2}}}\]
done
clear
D)
\[\propto \frac{1}{s}\]
done
clear
View Answer play_arrow
question_answer 190) The point in the interval\[[0,\,\,2\pi ]\], where\[f(x)={{e}^{x}}\sin x\]has maximum slope, is
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[\pi \]
done
clear
D)
\[\frac{3\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 191) The function\[f(x)=\frac{ax+b}{(x-1)(x-4)}\]has a local maxima at\[(2,\,\,-1)\], then
A)
\[b=1,\,\,a=0\]
done
clear
B)
\[b=1,\,\,a=0\]
done
clear
C)
\[b=-1,\,\,a=0\]
done
clear
D)
\[a=-1,\,\,b=0\]
done
clear
View Answer play_arrow
question_answer 192) If\[z=\tan (y+ax)+\sqrt{y-ax}\], then\[{{z}_{xx}}-{{a}^{2}}{{z}_{yy}}\]is equal to
A)
\[0\]
done
clear
B)
\[2\]
done
clear
C)
\[{{z}_{x}}+{{z}_{y}}\]
done
clear
D)
\[{{z}_{x}}{{z}_{y}}\]
done
clear
View Answer play_arrow
question_answer 193) If\[\int{f(x)dx}=F(x)\], then\[\int{{{x}^{3}}}f{{(x)}^{2}}dx\]is equal to
A)
\[\frac{1}{2}[{{x}^{2}}{{\{F(x)\}}^{2}}-\int{{{\{F(x)\}}^{2}}dx]}\]
done
clear
B)
\[\frac{1}{2}[{{x}^{2}}F{{(x)}^{2}}-\int{F{{(x)}^{2}}d{{(x)}^{2}}]}\]
done
clear
C)
\[\frac{1}{2}[{{x}^{2}}F(x)-\frac{1}{2}\int{{{\{F(x)\}}^{2}}dx]}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 194) \[\int{\frac{{{x}^{2}}+4}{{{x}^{4}}+16}}\]is equal to
A)
\[\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\left( \frac{{{x}^{2}}+4}{2x} \right)+c\]
done
clear
B)
\[\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\left( \frac{{{x}^{2}}-4}{2\sqrt{2x}} \right)+c\]
done
clear
C)
\[\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\left( \frac{{{x}^{2}}+4}{2\sqrt{2x}} \right)+c\]
done
clear
D)
\[\frac{1}{2}{{\tan }^{-1}}\left( \frac{{{x}^{2}}-4}{2x} \right)+c\]
done
clear
View Answer play_arrow
question_answer 195) Evaluate\[\int{\frac{1}{(x+1)\sqrt{{{x}^{2}}-1}}dx}\]
A)
\[\sqrt{\frac{x+1}{x-1}}+c\]
done
clear
B)
\[\sqrt{\frac{x-1}{x+1}}+c\]
done
clear
C)
\[\sqrt{\frac{1}{x+1}}+c\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 196) The value of the integral\[\int_{\pi /2}^{3\pi /2}{[\sin x]dx}\], where \[[\cdot ]\]denotes the greatest integer function, is
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[-\frac{\pi }{2}\]
done
clear
C)
\[0\]
done
clear
D)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 197) The area of the loop the curve \[a{{y}^{2}}={{x}^{2}}(a-x)\]is
A)
\[\frac{8{{a}^{2}}}{15}sq\,\,unit\]
done
clear
B)
\[\frac{4{{a}^{2}}}{15}sq\,\,unit\]
done
clear
C)
\[\frac{2{{a}^{2}}}{15}sq\,\,unit\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 198) Solution of the differential equation \[x=1+xy\frac{dy}{dx}+\frac{{{(xy)}^{2}}}{2!}{{\left( \frac{dy}{dx} \right)}^{2}}\]\[+\frac{{{(xy)}^{3}}}{3!}{{\left( \frac{dy}{dx} \right)}^{3}}+...\]is
A)
\[y={{\log }_{e}}(x)+c\]
done
clear
B)
\[y={{({{\log }_{e}}x)}^{2}}+c\]
done
clear
C)
\[y=\pm \sqrt{{{({{\log }_{e}}x)}^{2}}+2c}\]
done
clear
D)
\[xy={{x}^{y}}=k\]
done
clear
View Answer play_arrow
question_answer 199) If the solution of the differential equation\[\frac{dy}{dx}=\frac{ax+3}{2y+f}\]represents a circle, then the value of\[a\]is
A)
2
done
clear
B)
-2
done
clear
C)
3
done
clear
D)
-4
done
clear
View Answer play_arrow
question_answer 200) The approximate value of\[\int_{1}^{5}{{{x}^{2}}dx}\]using trapezoidal rule with n = 4 is
A)
41
done
clear
B)
41.5
done
clear
C)
41.75
done
clear
D)
42
done
clear
View Answer play_arrow
question_answer 201) MOSQUERADE
A)
to provide support
done
clear
B)
to go in disguise
done
clear
C)
to mesmerize
done
clear
D)
marathon race
done
clear
View Answer play_arrow
question_answer 202) PREPOSTEROUS
A)
careful
done
clear
B)
casual
done
clear
C)
absurd
done
clear
D)
deterrent
done
clear
View Answer play_arrow
question_answer 203) SOLITUDE
A)
musical composition
done
clear
B)
aloneness
done
clear
C)
true statement
done
clear
D)
single mindedness
done
clear
View Answer play_arrow
question_answer 204) PROPITIOUS
A)
favorable
done
clear
B)
clean
done
clear
C)
nearby
done
clear
D)
patriotic
done
clear
View Answer play_arrow
question_answer 205) RELENTLESS
A)
merciless
done
clear
B)
yielding
done
clear
C)
monotonous
done
clear
D)
incisive
done
clear
View Answer play_arrow
question_answer 206) FORBEARANCE
A)
patience
done
clear
B)
self-control
done
clear
C)
intolerance
done
clear
D)
preference
done
clear
View Answer play_arrow
question_answer 207) PALTRY
A)
absolete
done
clear
B)
cautious
done
clear
C)
random
done
clear
D)
plentiful
done
clear
View Answer play_arrow
question_answer 208) EXODUS
A)
influx
done
clear
B)
return
done
clear
C)
home coming
done
clear
D)
restoration
done
clear
View Answer play_arrow
question_answer 209) The........argument put forth for not disclosing the facts did not impress anybody.
A)
intemperate
done
clear
B)
spurious
done
clear
C)
specious
done
clear
D)
convincing
done
clear
View Answer play_arrow
question_answer 210) Director, he said, would.......the matter at once.
A)
invigilate
done
clear
B)
explore
done
clear
C)
investigate
done
clear
D)
survey
done
clear
View Answer play_arrow
question_answer 211) Everyone was.........by surprise when she announced her plan to marry that boy,
A)
moved
done
clear
B)
shaken
done
clear
C)
taken
done
clear
D)
prevailed
done
clear
View Answer play_arrow
question_answer 212) Your case is so unique that I am not getting any........to support it.
A)
reason
done
clear
B)
help
done
clear
C)
happening
done
clear
D)
precedent
done
clear
View Answer play_arrow
question_answer 213) The writing or compiling of dictionaries
A)
Lexicography
done
clear
B)
Numismatics
done
clear
C)
Cytology
done
clear
D)
Demography
done
clear
View Answer play_arrow
question_answer 214) The study of Insects
A)
Chromatics
done
clear
B)
Dactylology
done
clear
C)
Calligraphy
done
clear
D)
Entomology
done
clear
View Answer play_arrow
question_answer 215) Murder of ones brother
A)
Regiside
done
clear
B)
Foeticide
done
clear
C)
Fratricide
done
clear
D)
Uxoricide
done
clear
View Answer play_arrow
question_answer 216) Government by one person
A)
Autonomy
done
clear
B)
Autocracy
done
clear
C)
Plutocracy
done
clear
D)
Theocracy
done
clear
View Answer play_arrow
question_answer 217) She cut a sad figure in her first performance on the stage.
A)
made a sorry figure
done
clear
B)
cut a sorry face
done
clear
C)
cut a sorry figure
done
clear
D)
no improvement
done
clear
View Answer play_arrow
question_answer 218) No sooner I saw the tiger, than I ran away.
A)
as soon as I saw
done
clear
B)
no sooner 1 had seen
done
clear
C)
no sooner did I see
done
clear
D)
no improvement
done
clear
View Answer play_arrow
question_answer 219) If he had time he will call you.
A)
would have
done
clear
B)
would have had
done
clear
C)
has
done
clear
D)
no improvement
done
clear
View Answer play_arrow
question_answer 220) AH his answers were correct.
A)
his nil answers
done
clear
B)
his every answers
done
clear
C)
all of his answers
done
clear
D)
no improvement
done
clear
View Answer play_arrow
question_answer 221) Jam : Jelly : Pickles
A)
Butter : Marmalade : Grapes
done
clear
B)
Granite : Basalt : Coke
done
clear
C)
Cow : Dry : Draft
done
clear
D)
Bleat : Bray : Grunt
done
clear
View Answer play_arrow
question_answer 222) Mountain : Height : Climber
A)
River : Length : Water
done
clear
B)
Land : Farmer : Crop
done
clear
C)
College : Building : Student
done
clear
D)
Sea : Depth : Diver
done
clear
View Answer play_arrow
question_answer 223) Head : Brain : Think
A)
Eyes : Lashes : See
done
clear
B)
Skin : Sweat: Touch
done
clear
C)
Feet: Dance : Toe
done
clear
D)
Mouth : Teeth : Chew
done
clear
View Answer play_arrow
question_answer 224) Jute : Cotton : Wool
A)
Potato : Carrot : Bean
done
clear
B)
Canada : Chile : Asia
done
clear
C)
Liver ; Heat : Blood
done
clear
D)
Shark : Cod : Eel
done
clear
View Answer play_arrow
question_answer 225) Sial ; Sima ; Mantle
A)
Core : Asteroid : Comet
done
clear
B)
Pneumonia : Tetanus : Hepatitis
done
clear
C)
Calcite : Magnesium : Zinc
done
clear
D)
Wrestling : Karate : Boxing
done
clear
View Answer play_arrow
question_answer 226) Rourkela : Bokaro : Durgapur
A)
They have steel plants
done
clear
B)
They have coal mines
done
clear
C)
They have atomic power plants
done
clear
D)
They have the best technical colleges
done
clear
View Answer play_arrow
question_answer 227) Chlorine : Fluorine : Iodine
A)
These are names of inert gases
done
clear
B)
These are gases at room temperature
done
clear
C)
These are transition elements
done
clear
D)
These are halogens
done
clear
View Answer play_arrow
question_answer 228) Petrol : Phosphorus : Cooking gas
A)
They are fuels
done
clear
B)
They are highly in inflamable
done
clear
C)
They can be sold without permit
done
clear
D)
India has to import them
done
clear
View Answer play_arrow
question_answer 229) Green : Violet : Orange
A)
They arc primary colours
done
clear
B)
These colours occur together in a rainbow
done
clear
C)
They are made by mixing other colours
done
clear
D)
These colours are not found in butterflies
done
clear
View Answer play_arrow
question_answer 230) Supernova : Protostar : Red Giant
A)
These are kinds of stars
done
clear
B)
These are members of galaxies
done
clear
C)
These are stages in the life of a star
done
clear
D)
These move about the Sun
done
clear
View Answer play_arrow
question_answer 231) The classical dance, Kathakali belongs to
A)
Tamil Nadu
done
clear
B)
Karnataka
done
clear
C)
Orissa
done
clear
D)
Kerala
done
clear
View Answer play_arrow
question_answer 232) The highest civilian award in India is
A)
Paramveer Chakra
done
clear
B)
Bharat Ratna
done
clear
C)
Bhatnagar Award
done
clear
D)
Kalinga Award
done
clear
View Answer play_arrow
question_answer 233) Who is called Nightingale of India?
A)
Sarojini Naidu
done
clear
B)
Lata mangeshkar
done
clear
C)
Amir Khushro
done
clear
D)
Asha Bhosale
done
clear
View Answer play_arrow
question_answer 234) Nehru Trophy is related with
A)
Cricket
done
clear
B)
Volleyball
done
clear
C)
Hockey
done
clear
D)
Badminton
done
clear
View Answer play_arrow
question_answer 235) The headquarters of NATO is situated at
A)
Brussels
done
clear
B)
Geneva
done
clear
C)
Newyork
done
clear
D)
Paris
done
clear
View Answer play_arrow
question_answer 236) The first Indian woman to swim across the English channel is
A)
Bachendri Pal
done
clear
B)
Santosh Yadav
done
clear
C)
Nirja Mishra
done
clear
D)
Aarti Saha
done
clear
View Answer play_arrow
question_answer 237) Which of the following river is related with Bhakra-Nagal Project?
A)
Ravi
done
clear
B)
Satluj
done
clear
C)
Gandak
done
clear
D)
Mahanadi
done
clear
View Answer play_arrow
question_answer 238) Namdhapha National Park is located in
A)
Rajasthan
done
clear
B)
Orissa
done
clear
C)
Arunachal Pradesh
done
clear
D)
Uttar Pradesh
done
clear
View Answer play_arrow
question_answer 239) Which of the following is known as evening star?
A)
Venus
done
clear
B)
Mercury
done
clear
C)
Saturn
done
clear
D)
Jupiter
done
clear
View Answer play_arrow
question_answer 240) Which of the following was the founder of Indian National Congress?
A)
Jawahar Lal Nehru
done
clear
B)
Mahatma Gandhi
done
clear
C)
Moti Lal Nehru
done
clear
D)
A. O. Hume
done
clear
View Answer play_arrow