Introduction of Linear Equation
An algebraic equation is an equality involving one or more variables. It has equality sign in between. The expression on the left is called LHS and the expression on the right is called RHS. An expression in one variable having degree one is called linear equation in one variable. In a linear equation the value of the expression on LHS and RHS are all equal. The value of the variable which satisfies the given expression is called solution of the linear equation. We can find the solution of the linear equation either by hit and trial method or by solving the given equation for the required variables.
How to solve Linear Equation in One Variable
There are some set of rules to solve linear equation in one variable:
Properties of Equality
Let us consider an algebraic expression as A, B and C.
Property 1:
Addition Property of Equality.
If \[\text{A}=\text{B}\] then \[\text{A}+\text{C}=\text{B}+\text{C}\]
Property 2:
Subtraction Property of Equality.
If\[\text{A}=\text{B}\] then \[\text{A}-\text{C}=\text{B}-\text{C}\]
Property 3:
Multiplication Property of Equality.
If\[\text{A}=\text{B}\] and \[C\ne 0\] then CA = CB.
Property 4:
Division Property of Equality.
If\[\text{A}=\text{B}\] and \[C\ne 0\] then \[\frac{A}{C}=\frac{B}{C}\]
Note: Multiplying or dividing both sides of an equation by zero is carefully avoided. Dividing by zero is undefined and multiplying both sides by zero will result in an equation 0=0.
Degree of the Polynomials
The degree of the polynomials is the highest of power of the variable in the given polynomials. If the degree of the polynomial is zero then it is called constant polynomial.
If the degree of the polynomial is one then it is called linear polynomial and if the degree of the polynomial is two then it is called quadratic polynomial. For cubic polynomial the degree is three and if the degree is four then it is called biquadrate polynomial.
The polynomial \[ax+b=0\] is a linear polynomial.
The polynomial \[a{{x}^{2}}+bx+c=0\] is a quadratic polynomial.
The polynomial \[d{{x}^{3}}+a{{x}^{2}}+bx+c=0\] is a cubic polynomial.
The polynomial \[e{{x}^{4}}+d{{x}^{3}}+a{{x}^{2}}+bx+c=0\] is a biquadrate polynomial.
Factories: \[{{\text{y}}^{\text{2}}}+\text{3y}+\text{y}+\text{3}\]
Solution:
\[={{y}^{2}}+3y+y+3=y(y+3)+1(y+3)=(y+3)(y+1)\]
Factories: \[{{x}^{2}}+\frac{1}{{{x}^{2}}}+2-2x-\frac{2}{x}\]
Solution:
\[={{x}^{2}}+\frac{1}{{{x}^{2}}}+2-2x-\frac{2}{x}=\]\[{{\left( x+\frac{1}{x} \right)}^{2}}-2\left( x+\frac{1}{x} \right)=\] \[\left( x+\frac{1}{x} \right)\left( x+\frac{1}{x}-2 \right)\]
Factories \[4{{x}^{2}}+20x+3xy+15y\] and choose the correct option.
(a) \[(x+5)(4x+3y)\]
(b) \[(x-5)(5x+3y)\]
(c) \[(x+5)(5x-3y)\]
(d) \[(x+5)(x+3y)\]
(e) None of these
Answer: (a)
Explanation:
\[=(4{{x}^{2}}+20x)+(3yx+15y)\] \[=4x(x+5)+2y(x+5)\] \[=(x+5)(4x+3y)\]
Factories \[{{x}^{3}}-27\] and choose the correct option.
(a) \[(x-3)({{x}^{2}}+3x+9)\]
(b)\[(x+3)({{x}^{2}}+3x+9)\]
(c) \[(x-3)({{x}^{2}}-3x+9)\]
(d)\[(x-3)({{x}^{2}}+3x-9)\]
(e) None of these
Answer: (a)
Explanation:
\[{{x}^{3}}-27=(x-3)({{x}^{2}}+3x+9)\]
Factories the given polynomial \[\frac{9}{16}{{x}^{2}}+\frac{4}{9}{{y}^{2}}+4{{z}^{2}}-xy-\frac{8}{3}yz+3zx\].
(a) \[{{\left( \frac{3}{4}x-\frac{2}{3}y+2z \right)}^{2}}\]
(b) \[{{\left( \frac{3}{4}x+\frac{2}{3}y+2z \right)}^{2}}\]
(c) \[{{\left( \frac{3}{4}x+\frac{2}{3}y-2z \right)}^{2}}\]
(d) \[{{\left( \frac{3}{4}x-\frac{2}{3}y-2z \right)}^{2}}\]
(e) None of these
Answer: (a)
Factories the given polynomial \[36{{u}^{2}}+\frac{1}{25}{{v}^{2}}+25{{w}^{2}}-\frac{12}{5}uv-\frac{8}{5}vw+48wu\].
(a) \[{{\left( 6u-\frac{v}{5}-5w \right)}^{2}}\]
(b) \[{{\left( 6u+\frac{v}{5}-5w \right)}^{2}}\]
(c) \[{{\left( 6u-\frac{v}{5}+5w \right)}^{2}}\]
(d) \[{{\left( 6u+\frac{v}{5}+5w \right)}^{2}}\]
(e) None of these
Answer: (c)
Simplify the given expression: \[=\frac{0.86\times 0.86\times 0.86+0.14\times 0.14\times 0.14}{0.86\times 0.86-0.86\times more... 
Methods of Factorization
Different algebraic expressions can be factorized by different methods. Monomials can be easily written into their linear factors. Binomials can be factorized by using identities given in previous chapter. The quadratic equation can be factorized by splitting the middle term and cubic equation can be factorized by first dividing it by linear factors and then reducing it to the quadratic form and then applying the middle term splitting.
The other methods of factorization are by grouping the terms having the common coefficients or having some common variables. 
Introduction
Factorization of an algebraic expression is the process of writing the algebraic expression as a product of two or more linear factors. Each multiple of the algebraic expression is called factors of the algebraic expression. Thus the process of splitting the given algebraic expression into the product of two or more linear factors is called factorization.
According to the factor theorem if \[f(x)\] is polynomial which is completely divisible by another polynomials \[g(x)=x-a\], then \[x-a\] is called the factor of the polynomial \[f(x)\]and\[f(a)=0\] for all value of a. 
Cube Root of a Negative Number
The cube root of a negative number is always negative i.e. \[{{(-n)}^{\frac{1}{3}}}=-{{(n)}^{\frac{1}{3}}}\]
The cube root of -1000 is -10 because \[{{(-10)}^{3}}\]\[=-10\times -10\times -10=-1000\].
In symbolic form, the cube root of -1000 is written as \[\sqrt[3]{-1000}\]
So, \[\sqrt[3]{-1000}=-10\]
\[\because \]\[{{(-10)}^{3}}=-10\times -10\times -10=-1000\]
From the above, we can infer that:
Find the unit digit in the cube of the number 3331.
(a) 1
(b) 8
(c) 4
(d) 9
(e) None of these
Answer: (a)
Explanation:
We know that, \[{{\text{(3331)}}^{\text{3}}}=\text{3331}\times \text{3331}\times \text{3331}=\text{36959313691}\].
The smallest number by which 2560 must be multiplied so that the product will be a perfect cube.
(a) 35
(b) 25
(c) 8
(d) 5
(e) None of these
Answer: (b)
Explanation:
The factors of 2560 is given by
\[\text{256}0=\text{5}\times \text{8}\times \text{8}\times \text{8}\]
In this factors there are three 8 and one 5. So in order to make the number 5 perfect cube we have to multiply it by 25. Therefore, 25 is the least number by which it must be multiplied so that it becomes a perfect cube.
The smallest number by which we must divide 8788 so that it becomes a perfect cube.
(a) 2
(b) 169
(c) 4
(d) 13
(e) None of these
Answer: (c)
Find the value of \[{{\left[ {{({{5}^{2}}+{{12}^{2}})}^{\frac{1}{2}}} \right]}^{3}}\] is given by:
(a) 2197
(b) 169 more... 
Introduction
The word cube is used in geometry. In geometry the word cube refers to the solid having equal sides. Thus cube of a natural number is the multiple of three prime factors of each number. A given number is said to be a perfect cube if it can be expressed as a product of triplets of equal factors.
Cube of a Real Number
According to arithmetic and algebra, the cube of a number n is its third power. If a number multiplied three times by itself the resultant number is called cube of that number.
\[{{\text{n}}^{\text{3}}}=\text{n}\times \text{n}\times \text{n}\]. In this expression if \[\text{n}\times \text{n}\times \text{n}=\text{m}\] then we can say that m is cube of n. This is also the formula for volume of a geometric cube with sides of length "n".
The inverse operation of finding a number whose cube is 'n' is called finding the cube root of "n". It determines the side of the cube of a given volume.
Cubes of Certain Numbers which are Perfect Cube
\[{{1}^{3}}=1\] \[{{2}^{3}}=8\] \[{{3}^{3}}=27\] \[{{4}^{3}}=64\]
\[{{5}^{3}}=125\] \[{{6}^{3}}=216\] \[{{7}^{3}}=343\] \[{{8}^{3}}=512\]
\[{{9}^{3}}=729\] \[{{10}^{3}}=1000\] \[{{11}^{3}}=1331\] \[{{12}^{3}}=1728\]
\[{{13}^{3}}=2197\] \[{{14}^{3}}=2744\] \[{{15}^{3}}=3375\] \[{{16}^{3}}=4096\]
\[{{17}^{3}}=4913\] \[{{18}^{3}}=5832\] \[{{19}^{3}}=6859\] \[{{20}^{3}}=8000\]
Cube of a Negative Number
We know that the cube of a negative number is always negative.
\[{{(-1)}^{3}}=-1\times -1\times -1=-1\]
\[{{(-2)}^{3}}=-2\times -2\times -2=-8\]
\[{{(-3)}^{3}}=-3\times -3\times -3=-27\]
Cube Roots
The inverse operation of the cube of a number is called its cube root. It is normally denoted by. \[\sqrt[3]{n}\] or \[{{(n)}^{\frac{1}{3}}}\]. The cube root of a number can be found by using the prime factorization method.
A number is called cube root of its cube.
The cube root of 8 is 2 because \[{{2}^{3}}=2\times 2\times 2=8\]
In symbolic form, the cube root of 8 is written as \[\sqrt[3]{8}\]
Likewise:
\[\sqrt[3]{27}=3\] \[(\because \,{{3}^{3}}=3\times 3\times 3=27)\]
\[\sqrt[3]{64}=4\] \[(\because \,{{4}^{3}}=4\times 4\times 4=64)\]
\[\sqrt[3]{125}=5\] \[(\because {{5}^{3}}=5\times 5\times 5=125)\] 
Operation of Multiplication on Square Roots
We use the fact that the product of two radicals is the same as the radical of the product and vice versa.
we have, \[\sqrt{a}\times \sqrt{a}={{a}^{\frac{1}{2}}}\times {{a}^{\frac{1}{2}}}={{a}^{\frac{1}{2}+\frac{1}{2}}}={{a}^{1}}\] \[\therefore \]
\[\sqrt{3}\times \sqrt{3}=3\]
Also, \[\sqrt{3}\times \sqrt{5}=\sqrt{3\times 5}=\sqrt{15}\]
Problems Related to Navigation
A ship sails 42 km due east and then 25 km due north. How far is the ship from its starting position when it completes this voyage?
Solution:
Let the distance of the ship from its starting point be x km.
From the figure given below the distance is OP
Thus \[\Delta OPA\] is a right triangle with right angle at A.
Hence, by Pythagoras' Theorem,
\[O{{P}^{2}}=O{{A}^{2}}+A{{P}^{2}}\]
\[\Rightarrow \]\[{{x}^{2}}={{42}^{2}}+{{25}^{2}}\]\[\Rightarrow \]\[{{x}^{2}}=2389\]\[\Rightarrow \] \[x=\sqrt{2389}=48.88\,km\]
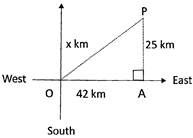
So, the ship is about 48.88 km far from the starting point.
The length of the diagonal of a rectangular paddock is 61 m and the length of one side is 60 m.
Find:
(a) The width of the paddock.
(b) The length of the fencing needed to enclose the paddock.
Solution:
(a) Let the width of the paddock be X By Pythagoras' Theorem, from the diagram given below.
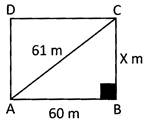
\[{{x}^{2}}={{61}^{2}}-{{60}^{2}}\]
\[{{x}^{2}}=3721-3600\]
\[{{x}^{2}}=121\]
\[x=\sqrt{121}\]
\[x=11\,m\]
So/the width of the paddock is 11 m.
(b) Now, Perimeter \[=\text{2(I}+\text{w)}\]
\[=\text{2(6}0+\text{11)}=\text{2}\times \text{71}=\text{142}\]
So, the length of the fence required to enclose the paddock is 142 m.
Use the information given in the diagram to find:
(a) Height of the triangle
(b) The area of the triangle
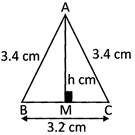
Solution:
(a) By Pythagoras' Theorem in \[\Delta \text{AMC}\],
By symmetry, M is the midpoint of BC;
\[\therefore \] \[MC\frac{1}{2}BC=\frac{3.2}{2}=1.6\,cm\]
\[{{h}^{2}}+{{1.6}^{2}}={{3.4}^{2}}\]
\[{{h}^{2}}+2.56=11.56\]
\[{{h}^{2}}=11.56-2.56\]
\[{{h}^{2}}=9\] \[h=\sqrt{9}=3\]
(b) Area of \[\Delta ABC=\frac{Base\times Height}{2}\]
\[=\frac{3.2\times 3}{2}=4.8\,cm\]
So, the area of \[\Delta \text{ABC is 4}. \text{8 c}{{\text{m}}^{\text{2}}}\]
Use the information given in the diagram to find the value of x.
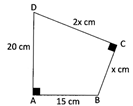
Solution:
Join BD of the quadrilateral to form the right-angled triangles \[\Delta \text{ABD}\] and \[\Delta BCD\].
Let BD = y cm.
By Pythagoras' Theorem in \[\Delta ABD\]
\[{{y}^{2}}={{15}^{2}}+{{20}^{2}}\]
\[=225+400\] \[=625\]
\[\Rightarrow \] \[y=\sqrt{625}=25\]
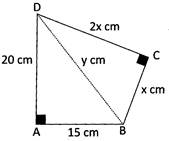
By Pythagoras' Theorem in \[\Delta \,\text{BCD}\]
\[{{x}^{2}}+{{(2x)}^{2}}={{y}^{2}}\]
\[(\because \,y=25)\] \[{{x}^{2}}+4{{x}^{2}}={{25}^{2}}\]
\[5{{x}^{2}}=625\] \[\Rightarrow \] \[\frac{5{{x}^{2}}}{5}=\frac{625}{5}\]
\[{{x}^{2}}=125\] \[\Rightarrow \] \[x=\sqrt{125}\]
\[x=\sqrt{25\times 5}\] \[\Rightarrow \] \[x=5\sqrt{5}\]
Adding and Subtracting Square Roots
Find the square root of \[21\frac{2797}{3364}\].
(a) \[\frac{289}{58}\]
(b) \[\frac{271}{58}\]
(c) \[\frac{281}{58}\]
(d) \[\frac{291}{58}\]
(e) None of these
Answer: (b)
Find the square root 0.000529.
(a) 0.023
(b) 0.027
(c) 0.033
(d) 0.037
(e) None of these
Answer: (a)
If \[\sqrt{2}=1.414,\sqrt{3}=1.732\] and \[\sqrt{\text{5}}=\text{2}.\text{236}\], then find the value of \[\sqrt{\frac{800}{45}}\].
(a) 5.214
(b) 4.216
(c) 4.214
(d) 5.216
(e) None of these
Answer: (b)
Simplify: \[\frac{\sqrt{1024}-\sqrt{324}}{\sqrt{441+\sqrt{196}}}\]
(a) \[\frac{2}{5}\]
(b) \[\sqrt{\frac{2}{5}}\]
(c) \[\sqrt{\frac{8}{5}}\]
(d) \[\sqrt{\frac{4}{25}}\]
(e) None of these
Answer: (a)
A rectangular garden is such that its length is twice the breath and its perimeter is equal to the perimetre of the square field whose area is given as \[\mathbf{5184}\text{ }{{\mathbf{m}}^{\mathbf{2}}}\]. The area of the rectangular field is:
(a) \[\text{56}0\text{8}\,{{\text{m}}^{\text{2}}}\]
(b) \[\text{46}0\text{8}\,{{\text{m}}^{\text{2}}}\]
(c) \[\text{36}0\text{8}\,{{\text{m}}^{\text{2}}}\]
(d) \[\text{24}0\text{8}\,{{\text{m}}^{\text{2}}}\]
(e) None of these
Answer: (b)
If \[\sqrt{4096}=64\] then find the value of \[\sqrt{4096}+\sqrt{4093}+\sqrt{0.004096}\].
(a) 70.646
(b) 60.464
(c) 70.464
(d) 60.646
(e) None of these
Answer: (c)
Find the value of 'y' such that \[\sqrt{188+\sqrt{53+\sqrt{y}}}=14\].
(a) 121
(b) 11
(c) 1331
(d) 161
(e) None of these
Answer: (a)
If \[\sqrt{1+\frac{25}{144}}=1+\frac{p}{12}\], then find the value of p for which this is satisfied.
(a) (-1, 25)
(b) (1, -25)
(c) (-1, -25)
(d) (1, 25)
(e) None of these
Answer: (b)
Find the value of y such that \[\sqrt{1+\sqrt{1-\frac{2176}{2401}}}=1+\frac{y}{7}\].
(a) (1, -15)
(b) (-1, -15)
(c) (1, 15)
(d) (-1, 15)
(e) None of these
Answer: (a) 
Finding Square Root of a Number by Division Method
We can find the square root by division method. The division method involves dividing the larger number by the smaller number and again the divisor with the remainder of the previous one and continue till the remainder becomes zero.
| 64 | |||
| 6 6 | 4096 36 | ||
| \[\sqrt{4096}\] | = | 124 4 | 496 496 |
| 128 | 0 |
Square Root Methods
We know that addition is inverse of subtraction, multiplication is inverse of division, and similarly square root is the inverse of square of a number. There are different methods to find the square root of a number. We can find the square root either by finding the factors or by repeated subtraction or by long division method.
By Prime Factorization Methods
In this method we find the prime factors of the given number and then pair them up. We multiply the numbers taking one from each pair and get the square root of the required number. It is useful only in case the numbers have perfect pairs of prime factors.
\[\sqrt{256}=\sqrt{(2\times 2)\times (2\times 2)\times (2\times 2)\times (2\times 2)}\]
There are four such order pairs within the square root of the number, therefore, the square root of the above number is \[\text{2}\times \text{2}\times \text{2}\times \text{2}=\text{16}\]
Repeated Subtraction Method
In this method we subtract the successive odd numbers from the given number starting from 1 till we get the result zero. The number of steps required to reduce the given number to zero will be the square root of the given number.
Take the number 64
Solution:
\[64-1=63\Rightarrow 63-3=60\Rightarrow 60-5=55\Rightarrow 55-7=48\]
\[\Rightarrow 48-9=39\Rightarrow 39-11=28\Rightarrow 28-13=15\Rightarrow 15-15=0\]
There are eight steps required to reduce the number to 0. Therefore, square root of 64 is 8.
Here are some more Squares and Square Roots
| \[\,Square\xrightarrow[{}]{{}}\] \[\xleftarrow[{}]{{}}\,Square\,Root\] | ||
| 4 | 16 | |
| 5 | 25 | |
| 6 | 36 | |
You need to login to perform this action.
You will be redirected in
3 sec
