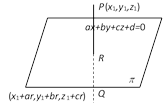
 (ii) Write the co-ordinates of image Q as \[({{x}_{1}}+ar,\,{{y}_{1}},\,+br,\,{{z}_{1}}+cr)\].
(iii) Find the co-ordinates of the mid-point R of PQ.
(iv) Obtain the value of r by putting the co-ordinates of R in the equation of the plane.
(v) Put the value of r in the co-ordinates of Q.
(ii) Write the co-ordinates of image Q as \[({{x}_{1}}+ar,\,{{y}_{1}},\,+br,\,{{z}_{1}}+cr)\].
(iii) Find the co-ordinates of the mid-point R of PQ.
(iv) Obtain the value of r by putting the co-ordinates of R in the equation of the plane.
(v) Put the value of r in the co-ordinates of Q.  Then \[x=x'+\alpha ,\text{ }y=y'\,+\beta \]
or \[x'=x-\alpha ,\text{ }y'=y-\beta \]
Thus if origin is shifted to point \[(\alpha ,\beta )\] without rotation of axes, then new equation of curve can be obtained by putting \[x+\alpha \] in place of \[x\] and \[y+\beta \] in place of \[y\].
(2) Rotation of axes without changing the origin : Let \[O\] be the origin. Let \[P\equiv (x,y)\] with respect to axes \[OX\] and \[OY\] and let \[P\equiv (x',y')\] with respect to axes \[OX'\] and \[OY'\] where \[\angle X'OX=\angle YOY'=\theta \]
Then \[x=x'+\alpha ,\text{ }y=y'\,+\beta \]
or \[x'=x-\alpha ,\text{ }y'=y-\beta \]
Thus if origin is shifted to point \[(\alpha ,\beta )\] without rotation of axes, then new equation of curve can be obtained by putting \[x+\alpha \] in place of \[x\] and \[y+\beta \] in place of \[y\].
(2) Rotation of axes without changing the origin : Let \[O\] be the origin. Let \[P\equiv (x,y)\] with respect to axes \[OX\] and \[OY\] and let \[P\equiv (x',y')\] with respect to axes \[OX'\] and \[OY'\] where \[\angle X'OX=\angle YOY'=\theta \]
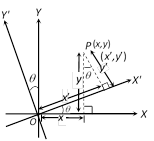 then \[x=x'\cos \theta -y'\sin \theta \]
\[y=x'\sin \theta +y'\cos \theta \]
and \[x'=x\cos \theta +y\sin \theta \]
\[y'=-x\sin \theta +y\cos \theta \]\[\]
The above relation between \[(x,y)\] and \[(x',y')\] can be easily obtained with the help of following table
then \[x=x'\cos \theta -y'\sin \theta \]
\[y=x'\sin \theta +y'\cos \theta \]
and \[x'=x\cos \theta +y\sin \theta \]
\[y'=-x\sin \theta +y\cos \theta \]\[\]
The above relation between \[(x,y)\] and \[(x',y')\] can be easily obtained with the help of following table
| \[x\downarrow \] | \[y\downarrow \] | |
| \[x'\to \] \[y'\to \] | \[\cos \theta \] \[-\sin \theta \] | \[\sin \theta \] \[\cos \theta \] |
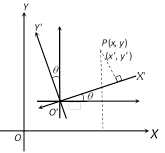 (4) Reflection (Image of a point) : Let \[(x,y)\]be any point, then its image with respect to
(i) x-axis \[\Rightarrow \] \[(x,-y)\] more...
(4) Reflection (Image of a point) : Let \[(x,y)\]be any point, then its image with respect to
(i) x-axis \[\Rightarrow \] \[(x,-y)\] more... You need to login to perform this action.
You will be redirected in
3 sec
