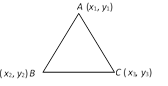
 \[\Delta =\frac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|\]\[=\frac{1}{2}\left| \text{ }({{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}})\text{ } \right|\]
In equilateral triangle
(i) Having sides a, area is \[\frac{\sqrt{3}}{4}{{a}^{2}}\].
(ii) Having length of perpendicular as 'p' area is \[\frac{({{p}^{2}})}{\sqrt{3}}\] .
(2) Collinear points : Three points \[A({{x}_{1}},{{y}_{1}}),\,\,B({{x}_{2}},{{y}_{2}}),\,C({{x}_{3}},{{y}_{3}})\] are collinear. If area of triangle is zero, then
(i) \[\Delta =0\] \[\Rightarrow \] \[\frac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|=0\] \[\Rightarrow \] \[\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|=0\]
(ii) \[AB+BC=AC\] or \[AC+BC=AB\] or \[AC+AB=BC\]
(3) Area of a quadrilateral : If \[({{x}_{1}},{{y}_{1}}),\,({{x}_{2}},{{y}_{2}}),\,\,({{x}_{3}},{{y}_{3}})\] and \[({{x}_{4}},{{y}_{4}})\] are vertices of a quadrilateral, then its area
\[=\frac{1}{2}[({{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}})+({{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}})+({{x}_{3}}{{y}_{4}}-{{x}_{4}}{{y}_{3}})+({{x}_{4}}{{y}_{1}}-{{x}_{1}}{{y}_{4}})]\]
(4) Area of polygon : The area of polygon whose vertices are \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}}),({{x}_{3}},{{y}_{3}}),....({{x}_{n,}}{{y}_{n}})\] is
\[=\,\frac{1}{2}|\{({{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}})+({{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}})+....+({{x}_{n}}{{y}_{1}}-{{x}_{1}}{{y}_{n}})\}|\]
Or Stair method : Repeat first co-ordinates one time in last for down arrow use positive sign and for up arrow use negative sign.
\[\therefore \] Area of polygon
\[\Delta =\frac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|\]\[=\frac{1}{2}\left| \text{ }({{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}})\text{ } \right|\]
In equilateral triangle
(i) Having sides a, area is \[\frac{\sqrt{3}}{4}{{a}^{2}}\].
(ii) Having length of perpendicular as 'p' area is \[\frac{({{p}^{2}})}{\sqrt{3}}\] .
(2) Collinear points : Three points \[A({{x}_{1}},{{y}_{1}}),\,\,B({{x}_{2}},{{y}_{2}}),\,C({{x}_{3}},{{y}_{3}})\] are collinear. If area of triangle is zero, then
(i) \[\Delta =0\] \[\Rightarrow \] \[\frac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|=0\] \[\Rightarrow \] \[\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ {{x}_{3}} & {{y}_{3}} & 1 \\ \end{matrix} \right|=0\]
(ii) \[AB+BC=AC\] or \[AC+BC=AB\] or \[AC+AB=BC\]
(3) Area of a quadrilateral : If \[({{x}_{1}},{{y}_{1}}),\,({{x}_{2}},{{y}_{2}}),\,\,({{x}_{3}},{{y}_{3}})\] and \[({{x}_{4}},{{y}_{4}})\] are vertices of a quadrilateral, then its area
\[=\frac{1}{2}[({{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}})+({{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}})+({{x}_{3}}{{y}_{4}}-{{x}_{4}}{{y}_{3}})+({{x}_{4}}{{y}_{1}}-{{x}_{1}}{{y}_{4}})]\]
(4) Area of polygon : The area of polygon whose vertices are \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}}),({{x}_{3}},{{y}_{3}}),....({{x}_{n,}}{{y}_{n}})\] is
\[=\,\frac{1}{2}|\{({{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}})+({{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}})+....+({{x}_{n}}{{y}_{1}}-{{x}_{1}}{{y}_{n}})\}|\]
Or Stair method : Repeat first co-ordinates one time in last for down arrow use positive sign and for up arrow use negative sign.
\[\therefore \] Area of polygon
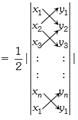 \[=\frac{1}{2}|\{({{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{3}}+....+{{x}_{n}}{{y}_{1}})-({{y}_{1}}{{x}_{2}}+{{y}_{2}}{{x}_{3}}+....+{{y}_{n}}{{x}_{1}})\}|\]
\[=\frac{1}{2}|\{({{x}_{1}}{{y}_{2}}+{{x}_{2}}{{y}_{3}}+....+{{x}_{n}}{{y}_{1}})-({{y}_{1}}{{x}_{2}}+{{y}_{2}}{{x}_{3}}+....+{{y}_{n}}{{x}_{1}})\}|\] 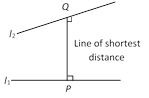 (2) Line of shortest distance : If \[{{l}_{1}}\] and \[{{l}_{2}}\] are two skew lines, then the straight line which is perpendicular to each of these two non-intersecting lines is called the “Line of shortest distance.”
There is one and only one line perpendicular to each of lines \[{{l}_{1}}\] and \[{{l}_{2}}\].
(3) Shortest distance between two skew lines
Let two skew lines be, \[\frac{x-{{x}_{1}}}{{{l}_{1}}}=\frac{y-{{y}_{1}}}{{{m}_{1}}}=\frac{z-{{z}_{1}}}{{{n}_{1}}}\] and \[\frac{x-{{x}_{2}}}{{{l}_{2}}}=\frac{y-{{y}_{2}}}{{{m}_{2}}}=\frac{z-{{z}_{2}}}{{{n}_{2}}}\]
Therefore, the shortest distance between the lines is given by \[d=\frac{\left| \,\begin{matrix} {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}} \\ {{l}_{1}} & {{m}_{1}} & {{n}_{1}} \\ {{l}_{2}} & {{m}_{2}} & {{n}_{2}} \\ \end{matrix}\, \right|}{\sqrt{{{({{m}_{1}}{{n}_{2}}-{{m}_{2}}{{n}_{1}})}^{2}}+{{({{n}_{1}}{{l}_{2}}-{{l}_{1}}{{n}_{2}})}^{2}}+{{({{l}_{1}}{{m}_{2}}-{{m}_{1}}{{l}_{2}})}^{2}}}}\].
(2) Line of shortest distance : If \[{{l}_{1}}\] and \[{{l}_{2}}\] are two skew lines, then the straight line which is perpendicular to each of these two non-intersecting lines is called the “Line of shortest distance.”
There is one and only one line perpendicular to each of lines \[{{l}_{1}}\] and \[{{l}_{2}}\].
(3) Shortest distance between two skew lines
Let two skew lines be, \[\frac{x-{{x}_{1}}}{{{l}_{1}}}=\frac{y-{{y}_{1}}}{{{m}_{1}}}=\frac{z-{{z}_{1}}}{{{n}_{1}}}\] and \[\frac{x-{{x}_{2}}}{{{l}_{2}}}=\frac{y-{{y}_{2}}}{{{m}_{2}}}=\frac{z-{{z}_{2}}}{{{n}_{2}}}\]
Therefore, the shortest distance between the lines is given by \[d=\frac{\left| \,\begin{matrix} {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}} \\ {{l}_{1}} & {{m}_{1}} & {{n}_{1}} \\ {{l}_{2}} & {{m}_{2}} & {{n}_{2}} \\ \end{matrix}\, \right|}{\sqrt{{{({{m}_{1}}{{n}_{2}}-{{m}_{2}}{{n}_{1}})}^{2}}+{{({{n}_{1}}{{l}_{2}}-{{l}_{1}}{{n}_{2}})}^{2}}+{{({{l}_{1}}{{m}_{2}}-{{m}_{1}}{{l}_{2}})}^{2}}}}\].
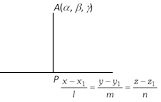 Length and equation of perpendicular : The length of the perpendicular is the distance AP and its equation is the line joining two known points A and P.
Length and equation of perpendicular : The length of the perpendicular is the distance AP and its equation is the line joining two known points A and P.
 The length of the perpendicular is the perpendicular distance of given point from that line.
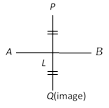
Reflection or image of a point in a straight line : If the perpendicular PL from point P on the given line be produced to Q such that \[PL=QL,\] then Q is known as the image or reflection of P in the given line. Also, L is the foot of the perpendicular or the projection of P on the line.
The length of the perpendicular is the perpendicular distance of given point from that line.
Reflection or image of a point in a straight line : If the perpendicular PL from point P on the given line be produced to Q such that \[PL=QL,\] then Q is known as the image or reflection of P in the given line. Also, L is the foot of the perpendicular or the projection of P on the line.
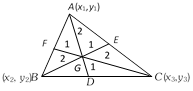 If \[A({{x}_{1}},{{y}_{1}})\], \[B({{x}_{2}},{{y}_{2}})\] and \[C({{x}_{3}},{{y}_{3}})\] are the vertices of a triangle. If G be the centroid upon one of the median (say) AD, then AG : GD = 2 : 1
\[\Rightarrow \] Co-ordinate of G are \[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]
(2) Circumcentre : The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle. It is the centre of the circle which passes through the vertices of the triangle and so its distance from the vertices of the triangle is the same and this distance is known as the circum-radius of the triangle.
If \[A({{x}_{1}},{{y}_{1}})\], \[B({{x}_{2}},{{y}_{2}})\] and \[C({{x}_{3}},{{y}_{3}})\] are the vertices of a triangle. If G be the centroid upon one of the median (say) AD, then AG : GD = 2 : 1
\[\Rightarrow \] Co-ordinate of G are \[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]
(2) Circumcentre : The circumcentre of a triangle is the point of intersection of the perpendicular bisectors of the sides of a triangle. It is the centre of the circle which passes through the vertices of the triangle and so its distance from the vertices of the triangle is the same and this distance is known as the circum-radius of the triangle.
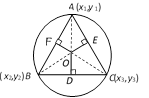 Let vertices A, B, C of the triangle ABC be \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})\] and \[({{x}_{3}},{{y}_{3}})\]and let circumcentre be \[O(x,\,\,y)\] and then \[(x,\,\,y)\] can be found by solving \[{{(OA)}^{2}}={{(OB)}^{2}}={{(OC)}^{2}}\]
i.e., \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}={{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}\]\[={{(x-{{x}_{3}})}^{2}}+{{(y-{{y}_{3}})}^{2}}\]
If a triangle is right angle, then its circumcentre is the mid point of hypotenuse. If angles of triangle i.e., A, B, C and vertices of triangle \[A({{x}_{1}},{{y}_{1}}),B({{x}_{2}},{{y}_{2}})\] and \[C\,({{x}_{3}},{{y}_{3}})\] are given, then circumcentre of the triangle ABC is
\[\left( \frac{{{x}_{1}}\sin 2A+{{x}_{2}}\sin 2B+{{x}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right.,\left. \frac{{{y}_{1}}\sin 2A+{{y}_{2}}\sin 2B+{{y}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right)\]
(3) Incentre : The incentre of a triangle is the point of intersection of internal bisector of the angles. Also it is a centre of a circle touching all the sides of a triangle.
Let vertices A, B, C of the triangle ABC be \[({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})\] and \[({{x}_{3}},{{y}_{3}})\]and let circumcentre be \[O(x,\,\,y)\] and then \[(x,\,\,y)\] can be found by solving \[{{(OA)}^{2}}={{(OB)}^{2}}={{(OC)}^{2}}\]
i.e., \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}={{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}\]\[={{(x-{{x}_{3}})}^{2}}+{{(y-{{y}_{3}})}^{2}}\]
If a triangle is right angle, then its circumcentre is the mid point of hypotenuse. If angles of triangle i.e., A, B, C and vertices of triangle \[A({{x}_{1}},{{y}_{1}}),B({{x}_{2}},{{y}_{2}})\] and \[C\,({{x}_{3}},{{y}_{3}})\] are given, then circumcentre of the triangle ABC is
\[\left( \frac{{{x}_{1}}\sin 2A+{{x}_{2}}\sin 2B+{{x}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right.,\left. \frac{{{y}_{1}}\sin 2A+{{y}_{2}}\sin 2B+{{y}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right)\]
(3) Incentre : The incentre of a triangle is the point of intersection of internal bisector of the angles. Also it is a centre of a circle touching all the sides of a triangle.
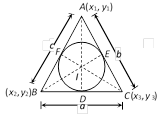 Co-ordinates of incentre
\[\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\]
where a, b, c are the sides of triangle ABC.
(4) Excircle : A circle touches one side outside the triangle and other two extended sides then circle is known as excircle. Let ABC be a triangle then there are three excircles with three excentres. Let \[{{I}_{1}},{{I}_{2}},{{I}_{3}}\] be the centres of ex-circles opposite to vertices A, B and C respectively. If vertices of triangle are \[A({{x}_{1}},{{y}_{1}}),\] \[B({{x}_{2}},{{y}_{2}})\] and \[C\,({{x}_{3}},{{y}_{3}})\], then
Co-ordinates of incentre
\[\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\]
where a, b, c are the sides of triangle ABC.
(4) Excircle : A circle touches one side outside the triangle and other two extended sides then circle is known as excircle. Let ABC be a triangle then there are three excircles with three excentres. Let \[{{I}_{1}},{{I}_{2}},{{I}_{3}}\] be the centres of ex-circles opposite to vertices A, B and C respectively. If vertices of triangle are \[A({{x}_{1}},{{y}_{1}}),\] \[B({{x}_{2}},{{y}_{2}})\] and \[C\,({{x}_{3}},{{y}_{3}})\], then
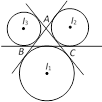 \[{{I}_{1}}\equiv \left( \frac{-a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{-a+b+c},\frac{-a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{-a+b+c} \right)\],
\[{{I}_{2}}\equiv \left( \frac{a{{x}_{1}}-b{{x}_{2}}+c{{x}_{3}}}{a-b+c},\frac{a{{y}_{1}}-b{{y}_{2}}+c{{y}_{3}}}{a-b+c} \right)\],
\[{{I}_{3}}\equiv \left( \frac{a{{x}_{1}}+b{{x}_{2}}-c{{x}_{3}}}{a+b-c},\frac{a{{y}_{1}}+b{{y}_{2}}-c{{y}_{3}}}{a+b-c} \right)\]
Angle bisector divides the opposite sides in the ratio of remaining sides e.g. \[\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\].
Incentre divides the angle bisectors in the ratio \[(b+c):a,\text{ }(c+a):b\] and \[(a+b):c\].
Excentre : Point of intersection of one internal angle bisector and other two external angle bisector is called as excentre. There are three excentres in a triangle. Co-ordinate of each can more...
\[{{I}_{1}}\equiv \left( \frac{-a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{-a+b+c},\frac{-a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{-a+b+c} \right)\],
\[{{I}_{2}}\equiv \left( \frac{a{{x}_{1}}-b{{x}_{2}}+c{{x}_{3}}}{a-b+c},\frac{a{{y}_{1}}-b{{y}_{2}}+c{{y}_{3}}}{a-b+c} \right)\],
\[{{I}_{3}}\equiv \left( \frac{a{{x}_{1}}+b{{x}_{2}}-c{{x}_{3}}}{a+b-c},\frac{a{{y}_{1}}+b{{y}_{2}}-c{{y}_{3}}}{a+b-c} \right)\]
Angle bisector divides the opposite sides in the ratio of remaining sides e.g. \[\frac{BD}{DC}=\frac{AB}{AC}=\frac{c}{b}\].
Incentre divides the angle bisectors in the ratio \[(b+c):a,\text{ }(c+a):b\] and \[(a+b):c\].
Excentre : Point of intersection of one internal angle bisector and other two external angle bisector is called as excentre. There are three excentres in a triangle. Co-ordinate of each can more... You need to login to perform this action.
You will be redirected in
3 sec
