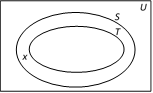
 Now, if we consider the statement : ? There are some scholars who are teachers?, It is evident from the Venn diagram that there is a scholar x who is not a teacher. Therefore, the above statement is false and its truth value is ?F?. Thus, we can also check the truth and falsity of other statements which are connected to a given statement.
Now, if we consider the statement : ? There are some scholars who are teachers?, It is evident from the Venn diagram that there is a scholar x who is not a teacher. Therefore, the above statement is false and its truth value is ?F?. Thus, we can also check the truth and falsity of other statements which are connected to a given statement. 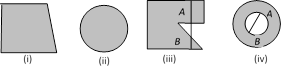 (i) and (ii) are convex set while (iii) and (iv) are not convex set.
(i) and (ii) are convex set while (iii) and (iv) are not convex set. 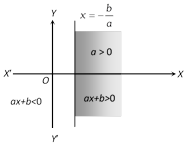 The graph of \[ax+b>0\] and \[ax+b<0\] are obtained by dividing xy-plane in two semi-planes by the line \[x=-\frac{b}{a}\](which is parallel to y-axis). Similarly for \[cy+d>0\]and \[cy+d<0\].
The graph of \[ax+b>0\] and \[ax+b<0\] are obtained by dividing xy-plane in two semi-planes by the line \[x=-\frac{b}{a}\](which is parallel to y-axis). Similarly for \[cy+d>0\]and \[cy+d<0\].
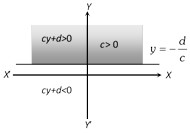
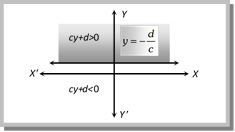 (ii) Linear Inequation in two variables : General form of these inequations are \[ax+by>c,ax+by<c\]. If any ordered pair \[\left( {{x}_{1}},{{y}_{1}} \right)\] satisfies an inequation, then it is said to be a solution of the inequation. The graph of these inequations is given below (for \[c>0\]) :
(ii) Linear Inequation in two variables : General form of these inequations are \[ax+by>c,ax+by<c\]. If any ordered pair \[\left( {{x}_{1}},{{y}_{1}} \right)\] satisfies an inequation, then it is said to be a solution of the inequation. The graph of these inequations is given below (for \[c>0\]) :
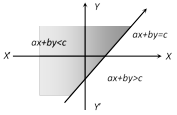 Working Rule : To draw the graph of an inequation, following procedure is followed :
(i) Write the equation \[ax+by=c\] in place of \[ax+by<c\] and \[ax+by>c\].
(ii) Make a table for the solutions of \[ax+by=c\].
(iii) Now draw a line with the help of these points. This is the graph of the line \[ax+by=c\].
(iv) If the inequation is > or <, then the points lying on this line is not considered and line is drawn dotted or discontinuous.
(v) If the ineuqation is \[\ge \] or\[\le \], then the points lying on the line is considered and line is drawn bold or continuous.
(vi) This line divides the plane XOY in two region.
To Find the region that satisfies the inequation, we apply the following rules:
(a) Take an arbitrary point which will be in either region.
(b) If it satisfies the given inequation, then the required region will be the region in which the arbitrary point is located.
(c) If it does not satisfy the inequation, then the other region is the required region.
(d) Draw the lines in the required region or make it shaded.
(2) Simultaneous linear inequations in two variables : Since the solution set of a system of simultaneous linear inequations is the set of all points in two dimensional space which satisfy all the inequations simultaneously. Therefore to find the solution set we find the region of the plane common to all the portions comprising the solution set of given inequations. In case there is no region common to all the solutions of the given inequations, we say that the solution set is void or empty.
(3) Feasible region : The limited (bounded) region of the graph made by two inequations is called feasible region. All the points in feasible region constitute the solution of a system of inequations. The feasible more...
Working Rule : To draw the graph of an inequation, following procedure is followed :
(i) Write the equation \[ax+by=c\] in place of \[ax+by<c\] and \[ax+by>c\].
(ii) Make a table for the solutions of \[ax+by=c\].
(iii) Now draw a line with the help of these points. This is the graph of the line \[ax+by=c\].
(iv) If the inequation is > or <, then the points lying on this line is not considered and line is drawn dotted or discontinuous.
(v) If the ineuqation is \[\ge \] or\[\le \], then the points lying on the line is considered and line is drawn bold or continuous.
(vi) This line divides the plane XOY in two region.
To Find the region that satisfies the inequation, we apply the following rules:
(a) Take an arbitrary point which will be in either region.
(b) If it satisfies the given inequation, then the required region will be the region in which the arbitrary point is located.
(c) If it does not satisfy the inequation, then the other region is the required region.
(d) Draw the lines in the required region or make it shaded.
(2) Simultaneous linear inequations in two variables : Since the solution set of a system of simultaneous linear inequations is the set of all points in two dimensional space which satisfy all the inequations simultaneously. Therefore to find the solution set we find the region of the plane common to all the portions comprising the solution set of given inequations. In case there is no region common to all the solutions of the given inequations, we say that the solution set is void or empty.
(3) Feasible region : The limited (bounded) region of the graph made by two inequations is called feasible region. All the points in feasible region constitute the solution of a system of inequations. The feasible more... You need to login to perform this action.
You will be redirected in
3 sec
