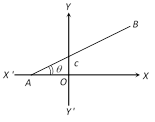
 The equation of a line with slope m and the x-intercept \[d\] is \[y=m(x-d)\].
(4) Intercept form : If a straight line cuts x-axis at A and the y-axis at B then OA and OB are known as the intercepts of the line on x-axis and y-axis respectively.
The equation of a line with slope m and the x-intercept \[d\] is \[y=m(x-d)\].
(4) Intercept form : If a straight line cuts x-axis at A and the y-axis at B then OA and OB are known as the intercepts of the line on x-axis and y-axis respectively.
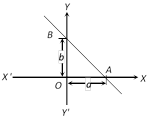 Then, equation of a straight line cutting off intercepts \[a\] and \[b\] on x–axis and y–axis respectively is \[\frac{x}{a}+\frac{y}{b}=1\].
If given line is parallel to \[X\] axis, then X-intercept is undefined.
If given line is parallel to \[Y\] axis, then Y-intercept is undefined.
(5) Two point form: Equation of the line through the points \[A({{x}_{1}},{{y}_{1}})\,\] and \[B({{x}_{2}},{{y}_{2}})\] is, \[(y-{{y}_{1}})=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}(x-{{x}_{1}})\].
Then, equation of a straight line cutting off intercepts \[a\] and \[b\] on x–axis and y–axis respectively is \[\frac{x}{a}+\frac{y}{b}=1\].
If given line is parallel to \[X\] axis, then X-intercept is undefined.
If given line is parallel to \[Y\] axis, then Y-intercept is undefined.
(5) Two point form: Equation of the line through the points \[A({{x}_{1}},{{y}_{1}})\,\] and \[B({{x}_{2}},{{y}_{2}})\] is, \[(y-{{y}_{1}})=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}(x-{{x}_{1}})\].
 In the determinant form it is gives as \[\left| \,\begin{matrix} x & y & 1 \\ {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ \end{matrix}\, \right|=0\] is the equation of line.
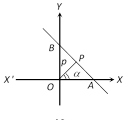
(6) Normal or perpendicular form : The equation of the straight line upon which the length of the perpendicular from the origin is \[p\] and this perpendicular makes an angle \[\alpha \] with x-axis is \[x\cos \alpha +y\sin \alpha =p\].
In the determinant form it is gives as \[\left| \,\begin{matrix} x & y & 1 \\ {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ \end{matrix}\, \right|=0\] is the equation of line.
(6) Normal or perpendicular form : The equation of the straight line upon which the length of the perpendicular from the origin is \[p\] and this perpendicular makes an angle \[\alpha \] with x-axis is \[x\cos \alpha +y\sin \alpha =p\].
 (7) Symmetrical or parametric or distance form of the line : Equation of a line passing through \[({{x}_{1}},{{y}_{1}})\] and making an angle q with the positive direction of x-axis is \[\frac{x-{{x}_{1}}}{\cos \theta }=\frac{y-{{y}_{1}}}{\sin \theta }=\pm r\], where r is the distance between the point \[P\,(x,\,\,y)\] and \[A({{x}_{1}},{{y}_{1}})\].
(7) Symmetrical or parametric or distance form of the line : Equation of a line passing through \[({{x}_{1}},{{y}_{1}})\] and making an angle q with the positive direction of x-axis is \[\frac{x-{{x}_{1}}}{\cos \theta }=\frac{y-{{y}_{1}}}{\sin \theta }=\pm r\], where r is the distance between the point \[P\,(x,\,\,y)\] and \[A({{x}_{1}},{{y}_{1}})\].
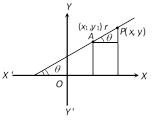 The co-ordinates of any point on this line may be taken as \[({{x}_{1}}\pm r\cos \theta ,{{y}_{1}}\pm r\sin \theta )\], known as parametric co-ordinates. \['r'\] is called the parameter.
The co-ordinates of any point on this line may be taken as \[({{x}_{1}}\pm r\cos \theta ,{{y}_{1}}\pm r\sin \theta )\], known as parametric co-ordinates. \['r'\] is called the parameter.
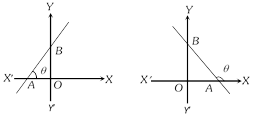 (1) Slope of line parallel to x – axis is \[m=\tan {{0}^{o}}=0\].
(2) Slope of line parallel to y – axis is \[m=\tan {{90}^{o}}=\infty \].
(3) Slope of the line equally inclined with the axes is 1 or – 1.
(4) Slope of the line through the points \[A({{x}_{1}},{{y}_{1}})\] and \[B({{x}_{2}},{{y}_{2}})\] is \[\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] taken in the same order.
(5) Slope of the line\[ax+by+c=0,b\ne 0\] is \[-\frac{a}{b}\].
(6) Slope of two parallel lines are equal.
(7) If \[{{m}_{1}}\] and \[{{m}_{2}}\] be the slopes of two perpendicular lines, then \[{{m}_{1}}.{{m}_{2}}=-1\].
(8) \[m\] can be defined as \[\tan \theta \] for \[0\le \theta \le \pi \] and \[\theta \ne \frac{\pi }{2}\].
(1) Slope of line parallel to x – axis is \[m=\tan {{0}^{o}}=0\].
(2) Slope of line parallel to y – axis is \[m=\tan {{90}^{o}}=\infty \].
(3) Slope of the line equally inclined with the axes is 1 or – 1.
(4) Slope of the line through the points \[A({{x}_{1}},{{y}_{1}})\] and \[B({{x}_{2}},{{y}_{2}})\] is \[\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] taken in the same order.
(5) Slope of the line\[ax+by+c=0,b\ne 0\] is \[-\frac{a}{b}\].
(6) Slope of two parallel lines are equal.
(7) If \[{{m}_{1}}\] and \[{{m}_{2}}\] be the slopes of two perpendicular lines, then \[{{m}_{1}}.{{m}_{2}}=-1\].
(8) \[m\] can be defined as \[\tan \theta \] for \[0\le \theta \le \pi \] and \[\theta \ne \frac{\pi }{2}\]. 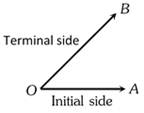 The motion of any revolving line in a plane from its initial position (initial side) to the final position (terminal side) is called angle. The end point O about which the line rotates is called the vertex of the angle.
The motion of any revolving line in a plane from its initial position (initial side) to the final position (terminal side) is called angle. The end point O about which the line rotates is called the vertex of the angle. You need to login to perform this action.
You will be redirected in
3 sec
