(1) Homogeneous differential equation : A function \[f(x,\,\,y)\]is called a homogeneous function of degree \[n\] if \[f(\lambda x,\lambda y\,)=\] \[{{\lambda }^{n}}\,f(x,y)\,\].
For example, \[f(x,y)={{x}^{2}}-{{y}^{2}}+3xy\] is a homogeneous function of degree 2. A homogenous function \[f(x,\,y)\] of degree \[n\] can always be written as \[f(x,\,y)={{x}^{n}}f\left( \frac{y}{x} \right)\] or\[f(x,y)={{y}^{n}}f\left( \frac{x}{y} \right)\]. If a first-order first-degree differential equation is expressible in the form \[\frac{dy}{dx}=\frac{f(x,\,y)}{g(x,y)}\] where \[f(x,\,\,y)\] and \[g(x,\,\,y)\] are homogeneous functions of the same degree, then it is called a homogeneous differential equation. Such type of equations can be reduced to variable separable form by the substitution \[y=vx\]. The given differential equation can be written as \[\frac{dy}{dx}=\frac{{{x}^{n}}f(y/x)}{{{x}^{n}}g(y/x)}\]\[=\frac{f(y/x)}{g(y/x)}\]\[=F\left( \frac{y}{x} \right)\]. If \[y=vx\], then \[\frac{dy}{dx}=v+x\frac{dv}{dx}\]. Substituting the value of \[\frac{dy}{dx}=F\left( \frac{y}{x} \right)\], we get \[v+x\frac{dv}{dx}=F(v)\]\[v+x\frac{dv}{dx}=F(v)\Rightarrow \frac{dv}{F(v)-v}=\frac{dx}{x}\].
On integration, \[\int{\frac{1}{F(v)-v}dv=\int{\frac{dx}{x}+c}}\] where \[c\] is an arbitrary constant of integration. After integration, \[v\] will be replaced by \[\frac{y}{x}\] in complete solution.
(2) Equation reducible to homogeneous form : A first order, first degree differential equation of the form
\[\frac{dy}{dx}=\frac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}\], where \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\] .....(i)
This is non-homogeneous.
It can be reduced to homogeneous form by certain substitutions. Put \[x=X+h,\,y=Y+k\].
Where \[h\] and \[k\] are constants, which are to be determined.
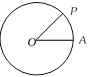
 i.e., Arc = radius \[\times \] angle in radians Sectorial area : Let OAB be a sector having central angle \[{{\theta }^{C}}\] and radius r. Then area of the sector OAB is given by \[\frac{1}{2}{{r}^{2}}\theta \].
i.e., Arc = radius \[\times \] angle in radians Sectorial area : Let OAB be a sector having central angle \[{{\theta }^{C}}\] and radius r. Then area of the sector OAB is given by \[\frac{1}{2}{{r}^{2}}\theta \]. 