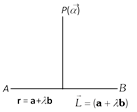
 (7) Perpendicular distance of a point from a line : Let L is the foot of perpendicular drawn from \[P(\vec{\alpha })\] on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. Since \[\mathbf{r}\] denotes the position vector of any point on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. So, let the position vector of \[\vec{L}\] be \[\mathbf{a}+\lambda \mathbf{b}\].
Then \[\overrightarrow{PL}=\mathbf{a}-\overrightarrow{\alpha }+\lambda \mathbf{b}=(\mathbf{a}-\overrightarrow{\alpha })-\left( \frac{(\mathbf{a}-\overrightarrow{\alpha })\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}\]
The length PL, is the magnitude of\[\overrightarrow{PL}\], and required length of perpendicular.
(7) Perpendicular distance of a point from a line : Let L is the foot of perpendicular drawn from \[P(\vec{\alpha })\] on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. Since \[\mathbf{r}\] denotes the position vector of any point on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. So, let the position vector of \[\vec{L}\] be \[\mathbf{a}+\lambda \mathbf{b}\].
Then \[\overrightarrow{PL}=\mathbf{a}-\overrightarrow{\alpha }+\lambda \mathbf{b}=(\mathbf{a}-\overrightarrow{\alpha })-\left( \frac{(\mathbf{a}-\overrightarrow{\alpha })\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}\]
The length PL, is the magnitude of\[\overrightarrow{PL}\], and required length of perpendicular.
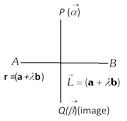 (8) Image of a point in a straight line : Let \[Q(\overrightarrow{\beta })\] is the image of P in \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\], then, \[\overrightarrow{\beta }=2\mathbf{a}-\left( \frac{2(\mathbf{a}-\overrightarrow{\alpha }).\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}-\overrightarrow{\alpha }\]
(9) Shortest distance between two parallel lines : Let \[{{l}_{1}}\] and \[{{l}_{2}}\] be two lines whose equations are \[{{l}_{1}}:\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[{{l}_{2}}:\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] respectively.
Then, shortest distance
\[PQ=\left| \frac{({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{\mathbf{2}}})\,.\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|=\left| \frac{[{{\mathbf{b}}_{1}}\text{ }{{\mathbf{b}}_{\mathbf{2}}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|\]
Shortest distance between two parallel lines : The shortest distance between the parallel lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \mathbf{b}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu \mathbf{b}\] is given by \[d=\frac{|({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\times \mathbf{b}|}{|\mathbf{b}|}\].
If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] intersect, then the shortest distance between them is zero.
Therefore, \[[{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]=0\]
\[\Rightarrow \]\[[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\,\,{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=0\]\[\Rightarrow \]\[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}}).({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}})=0\].
(10) If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \,{{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\lambda \,{{\mathbf{b}}_{2}}\] are coplanar, then \[[{{\mathbf{a}}_{1}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]\] and the equation of the plane containing them is \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{1}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\] or \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}\,{{\mathbf{b}}_{\mathbf{1}}}\,{{\mathbf{b}}_{\mathbf{2}}}]\].
(11) Vector equation of a plane through the point \[A(\mathbf{a})\] and perpendicular to the vector \[\mathbf{n}\] is \[(\mathbf{r}-\mathbf{a}).\mathbf{n}=0\] or \[\mathbf{r}.\mathbf{n}=\mathbf{a}.\mathbf{n}\] or \[\mathbf{r}\,.\,\mathbf{n}=d\], where \[d=\mathbf{a}\,.\,\mathbf{n}\]. This is known as the scalar product form of a plane.
(12) Vector equation of a plane normal to unit vector \[\mathbf{\hat{n}}\] and at a distance d from the origin is \[\mathbf{r}\mathbf{.\hat{n}}=d\].
If \[\mathbf{n}\] is not a unit vector, then to reduce the equation \[\mathbf{r}.\mathbf{n}=d\] to normal form we divide both sides by \[|\mathbf{n}|\] to obtain \[\mathbf{r}\cdot \frac{\mathbf{n}}{|\mathbf{n}|}=\frac{d}{|\mathbf{n}|}\] more...
(8) Image of a point in a straight line : Let \[Q(\overrightarrow{\beta })\] is the image of P in \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\], then, \[\overrightarrow{\beta }=2\mathbf{a}-\left( \frac{2(\mathbf{a}-\overrightarrow{\alpha }).\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}-\overrightarrow{\alpha }\]
(9) Shortest distance between two parallel lines : Let \[{{l}_{1}}\] and \[{{l}_{2}}\] be two lines whose equations are \[{{l}_{1}}:\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[{{l}_{2}}:\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] respectively.
Then, shortest distance
\[PQ=\left| \frac{({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{\mathbf{2}}})\,.\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|=\left| \frac{[{{\mathbf{b}}_{1}}\text{ }{{\mathbf{b}}_{\mathbf{2}}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|\]
Shortest distance between two parallel lines : The shortest distance between the parallel lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \mathbf{b}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu \mathbf{b}\] is given by \[d=\frac{|({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\times \mathbf{b}|}{|\mathbf{b}|}\].
If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] intersect, then the shortest distance between them is zero.
Therefore, \[[{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]=0\]
\[\Rightarrow \]\[[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\,\,{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=0\]\[\Rightarrow \]\[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}}).({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}})=0\].
(10) If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \,{{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\lambda \,{{\mathbf{b}}_{2}}\] are coplanar, then \[[{{\mathbf{a}}_{1}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]\] and the equation of the plane containing them is \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{1}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\] or \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}\,{{\mathbf{b}}_{\mathbf{1}}}\,{{\mathbf{b}}_{\mathbf{2}}}]\].
(11) Vector equation of a plane through the point \[A(\mathbf{a})\] and perpendicular to the vector \[\mathbf{n}\] is \[(\mathbf{r}-\mathbf{a}).\mathbf{n}=0\] or \[\mathbf{r}.\mathbf{n}=\mathbf{a}.\mathbf{n}\] or \[\mathbf{r}\,.\,\mathbf{n}=d\], where \[d=\mathbf{a}\,.\,\mathbf{n}\]. This is known as the scalar product form of a plane.
(12) Vector equation of a plane normal to unit vector \[\mathbf{\hat{n}}\] and at a distance d from the origin is \[\mathbf{r}\mathbf{.\hat{n}}=d\].
If \[\mathbf{n}\] is not a unit vector, then to reduce the equation \[\mathbf{r}.\mathbf{n}=d\] to normal form we divide both sides by \[|\mathbf{n}|\] to obtain \[\mathbf{r}\cdot \frac{\mathbf{n}}{|\mathbf{n}|}=\frac{d}{|\mathbf{n}|}\] more... 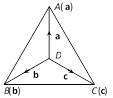 Volume of tetrahedron
(i) The volume of a tetrahedron \[=\frac{1}{3}(\text{area of the base) (corresponding altitude)}\]\[=\frac{1}{6}[\overrightarrow{AB}\,\text{ }\overrightarrow{BC}\,\text{ }\overrightarrow{AD}]\]
(ii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are position vectors of vertices \[A,\,\,B\] and \[C\] with respect to \[O,\] then volume of tetrahedron \[OABC=\frac{1}{6}\,[\mathbf{a}\,\,\mathbf{b}\ \,\mathbf{c}]\].
(iii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c},\,\mathbf{d}\] are position vectors of vertices \[A,B,C,D\] of a tetrahedron \[ABCD,\] then its volume \[=\frac{1}{6}[\mathbf{b}-\mathbf{a}\,\,\mathbf{c}-\mathbf{a}\,\,\mathbf{d}-\mathbf{a}]\].
(5) Reciprocal more...
Volume of tetrahedron
(i) The volume of a tetrahedron \[=\frac{1}{3}(\text{area of the base) (corresponding altitude)}\]\[=\frac{1}{6}[\overrightarrow{AB}\,\text{ }\overrightarrow{BC}\,\text{ }\overrightarrow{AD}]\]
(ii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are position vectors of vertices \[A,\,\,B\] and \[C\] with respect to \[O,\] then volume of tetrahedron \[OABC=\frac{1}{6}\,[\mathbf{a}\,\,\mathbf{b}\ \,\mathbf{c}]\].
(iii) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c},\,\mathbf{d}\] are position vectors of vertices \[A,B,C,D\] of a tetrahedron \[ABCD,\] then its volume \[=\frac{1}{6}[\mathbf{b}-\mathbf{a}\,\,\mathbf{c}-\mathbf{a}\,\,\mathbf{d}-\mathbf{a}]\].
(5) Reciprocal more... 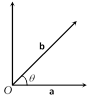 Then \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\]\[\sin \theta \,\hat{\eta }\], and \[|\mathbf{a}\times \mathbf{b}|\text{ }=\text{ }|\mathbf{a}||\mathbf{b}|\sin \theta \], where \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\hat{\eta }\] form a right-handed system.
(2) Properties of vector product
(i) Vector product is not commutative i.e., if \[\mathbf{a}\] and \[\mathbf{b}\] are any two vectors, then \[\mathbf{a}\times \mathbf{b}\ne \mathbf{b}\times \mathbf{a}\], however, \[\mathbf{a}\times \mathbf{b}=-(\mathbf{b}\times \mathbf{a})\]
(ii) If \[\mathbf{a},\,\mathbf{b}\] are two vectors and m, n are scalars, then \[m\mathbf{a}\times n\mathbf{b}=mn(\mathbf{a}\times \mathbf{b})=m\,(\mathbf{a}\times n\mathbf{b})=n(m\,\mathbf{a}\times \mathbf{b})\].
(iii) Distributivity of vector product over vector addition.
Let \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] be any three vectors. Then
(a) \[\mathbf{a}\times (\mathbf{b}+\mathbf{c})=\mathbf{a}\times \mathbf{b}+\mathbf{a}\times \mathbf{c}\] (Left distributivity)
(b) \[(\mathbf{b}+\mathbf{c})\times \mathbf{a}=\mathbf{b}\times \mathbf{a}+\mathbf{c}\times \mathbf{a}\] (Right distributivity)
(iv) For any three vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] we have \[\mathbf{a}\times (\mathbf{b}-\mathbf{c})=\] \[\mathbf{a}\times \mathbf{b}-\mathbf{a}\times \mathbf{c}\].
(v) The vector product of two non-zero vectors is zero vector iff they are parallel (Collinear) i.e., \[\mathbf{a}\times \mathbf{b}=0\Leftrightarrow \mathbf{a}||\mathbf{b},\,\mathbf{a},\,\mathbf{b}\] are non-zero vectors.
It follows from the above property that \[\mathbf{a}\times \mathbf{a}=0\] for every non-zero vector \[\mathbf{a}\], which in turn implies that \[\mathbf{i}\times \mathbf{i}=\] \[\mathbf{j}\times \mathbf{j}=\mathbf{k}\times \mathbf{k}=0\].
(vi) Vector product of orthonormal triad of unit vectors \[\mathbf{i},\text{ }\mathbf{j},\text{ }\mathbf{k}\] using the definition of the vector product, we obtain \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\], \[\mathbf{j}\times \mathbf{i}=-\mathbf{k},\,\mathbf{k}\times \mathbf{j}=-\mathbf{i},\,\mathbf{i}\times \mathbf{k}=-\mathbf{j}\].
(3) Vector product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\].
Then, \[\mathbf{a}\times \mathbf{b}=\left| \,\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ \end{matrix}\, \right|\]
(4) Angle between two vectors : If \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], then \[\sin \theta =\frac{|\mathbf{a}\times \mathbf{b}|}{|\mathbf{a}|\,|\mathbf{b}|}\].
(5) (i) Right handed system of vectors : Three mutually perpendicular vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] form a right handed system of vector iff \[\mathbf{a}\times \mathbf{b}=\mathbf{c},\,\,\mathbf{b}\times \mathbf{c}=\mathbf{a},\,\,\mathbf{c}\times \mathbf{a}=\mathbf{b}\]
Examples: The unit vectors \[\mathbf{i}\,\mathbf{,}\,\mathbf{j,}\,\,\mathbf{k}\] form a right-handed system, \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\]
Then \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\]\[\sin \theta \,\hat{\eta }\], and \[|\mathbf{a}\times \mathbf{b}|\text{ }=\text{ }|\mathbf{a}||\mathbf{b}|\sin \theta \], where \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\hat{\eta }\] form a right-handed system.
(2) Properties of vector product
(i) Vector product is not commutative i.e., if \[\mathbf{a}\] and \[\mathbf{b}\] are any two vectors, then \[\mathbf{a}\times \mathbf{b}\ne \mathbf{b}\times \mathbf{a}\], however, \[\mathbf{a}\times \mathbf{b}=-(\mathbf{b}\times \mathbf{a})\]
(ii) If \[\mathbf{a},\,\mathbf{b}\] are two vectors and m, n are scalars, then \[m\mathbf{a}\times n\mathbf{b}=mn(\mathbf{a}\times \mathbf{b})=m\,(\mathbf{a}\times n\mathbf{b})=n(m\,\mathbf{a}\times \mathbf{b})\].
(iii) Distributivity of vector product over vector addition.
Let \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] be any three vectors. Then
(a) \[\mathbf{a}\times (\mathbf{b}+\mathbf{c})=\mathbf{a}\times \mathbf{b}+\mathbf{a}\times \mathbf{c}\] (Left distributivity)
(b) \[(\mathbf{b}+\mathbf{c})\times \mathbf{a}=\mathbf{b}\times \mathbf{a}+\mathbf{c}\times \mathbf{a}\] (Right distributivity)
(iv) For any three vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] we have \[\mathbf{a}\times (\mathbf{b}-\mathbf{c})=\] \[\mathbf{a}\times \mathbf{b}-\mathbf{a}\times \mathbf{c}\].
(v) The vector product of two non-zero vectors is zero vector iff they are parallel (Collinear) i.e., \[\mathbf{a}\times \mathbf{b}=0\Leftrightarrow \mathbf{a}||\mathbf{b},\,\mathbf{a},\,\mathbf{b}\] are non-zero vectors.
It follows from the above property that \[\mathbf{a}\times \mathbf{a}=0\] for every non-zero vector \[\mathbf{a}\], which in turn implies that \[\mathbf{i}\times \mathbf{i}=\] \[\mathbf{j}\times \mathbf{j}=\mathbf{k}\times \mathbf{k}=0\].
(vi) Vector product of orthonormal triad of unit vectors \[\mathbf{i},\text{ }\mathbf{j},\text{ }\mathbf{k}\] using the definition of the vector product, we obtain \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\], \[\mathbf{j}\times \mathbf{i}=-\mathbf{k},\,\mathbf{k}\times \mathbf{j}=-\mathbf{i},\,\mathbf{i}\times \mathbf{k}=-\mathbf{j}\].
(3) Vector product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\].
Then, \[\mathbf{a}\times \mathbf{b}=\left| \,\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ \end{matrix}\, \right|\]
(4) Angle between two vectors : If \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], then \[\sin \theta =\frac{|\mathbf{a}\times \mathbf{b}|}{|\mathbf{a}|\,|\mathbf{b}|}\].
(5) (i) Right handed system of vectors : Three mutually perpendicular vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] form a right handed system of vector iff \[\mathbf{a}\times \mathbf{b}=\mathbf{c},\,\,\mathbf{b}\times \mathbf{c}=\mathbf{a},\,\,\mathbf{c}\times \mathbf{a}=\mathbf{b}\]
Examples: The unit vectors \[\mathbf{i}\,\mathbf{,}\,\mathbf{j,}\,\,\mathbf{k}\] form a right-handed system, \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\]
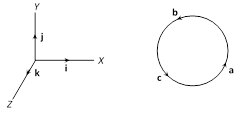 (ii) Left handed system of vectors : The vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] mutually perpendicular to one another form a left handed system of vector iff \[\mathbf{c}\times \mathbf{b}=\mathbf{a},\,\mathbf{a}\times \mathbf{c}=\mathbf{b},\mathbf{b}\times \mathbf{a}=\mathbf{c}\]
(ii) Left handed system of vectors : The vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] mutually perpendicular to one another form a left handed system of vector iff \[\mathbf{c}\times \mathbf{b}=\mathbf{a},\,\mathbf{a}\times \mathbf{c}=\mathbf{b},\mathbf{b}\times \mathbf{a}=\mathbf{c}\]
 (6) Vector normal to the plane of two given vectors : If \[\mathbf{a},\,\mathbf{b}\] be two non-zero, nonparallel vectors and let \[\theta \] be the angle between them. \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\sin \theta \,\hat{\eta }\] where \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\eta \] form a right-handed system.
\[\Rightarrow \] \[(\mathbf{a}\times \mathbf{b})=|\mathbf{a}\times \mathbf{b}|\,\hat{\eta }\]\[\Rightarrow \] \[\hat{\eta }=\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\]
Thus, \[\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is a unit vector perpendicular to the plane of \[-\frac{\sqrt{3}}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}\] and \[\mathbf{b}\]. Note that \[-\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is also more...
(6) Vector normal to the plane of two given vectors : If \[\mathbf{a},\,\mathbf{b}\] be two non-zero, nonparallel vectors and let \[\theta \] be the angle between them. \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\sin \theta \,\hat{\eta }\] where \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\eta \] form a right-handed system.
\[\Rightarrow \] \[(\mathbf{a}\times \mathbf{b})=|\mathbf{a}\times \mathbf{b}|\,\hat{\eta }\]\[\Rightarrow \] \[\hat{\eta }=\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\]
Thus, \[\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is a unit vector perpendicular to the plane of \[-\frac{\sqrt{3}}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}\] and \[\mathbf{b}\]. Note that \[-\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is also more... 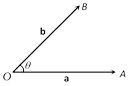 Angle between two vectors : If \[\mathbf{a},\,\mathbf{b}\] be two vectors inclined at an angle \[\theta \], then \[\mathbf{a}\,.\,\mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\,\cos \theta \]
\[\Rightarrow \] \[\cos \theta =\frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|}\]\[\Rightarrow \] \[\theta ={{\cos }^{-1}}\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|} \right)\]
If \[\mathbf{a}\,={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\]; then
\[\theta ={{\cos }^{-1}}\left( \frac{{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}} \right)\].
(2) Properties of scalar product
(i) Commutativity : The scalar product of two vector is commutative i.e., \[\mathbf{a}\,.\,\mathbf{b}\,=\mathbf{b}\,.\,\mathbf{a}\].
(ii) Distributivity of scalar product over vector addition The scalar product of vectors is distributive over vector addition i.e., (a) \[\mathbf{a}\,.\,(\mathbf{b}\,+\mathbf{c})\,=\,\mathbf{a}\,.\,\mathbf{b}+\mathbf{a}\,.\,\mathbf{c}\], (Left distributivity)
(b) \[(\mathbf{b}+\mathbf{c})\,.\,\mathbf{a}=\mathbf{b}\,.\,\mathbf{a}+\mathbf{c}\,.\,\mathbf{a}\], (Right distributivity)
(iii) Let \[\mathbf{a}\] and \[\mathbf{b}\] be two non-zero vectors \[\mathbf{a}\,.\,\mathbf{b}=0\Leftrightarrow \mathbf{a}\bot \mathbf{b}\].
As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are mutually perpendicular unit vectors along the co-ordinate axes, therefore, \[\mathbf{i}\,.\,\mathbf{j}=\mathbf{j}\,.\,\mathbf{i}=0\]; \[\mathbf{j}\,.\,\mathbf{k}=\mathbf{k}\,.\,\mathbf{j}=0;\] \[\mathbf{k}\,.\,\mathbf{i}=\mathbf{i}\,.\,\mathbf{k}\,=0\].
(iv) For any vector \[\mathbf{a},\,\text{ }\mathbf{a}\,.\,\mathbf{a}=|\mathbf{a}{{|}^{2}}\].
As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are unit vectors along the co-ordinate axes, therefore \[\mathbf{i}\,.\,\mathbf{i}=|\mathbf{i}{{|}^{2}}=1\], \[\mathbf{j}\,.\,\mathbf{j}=|\mathbf{j}{{|}^{2}}=1\] and \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}+\mu \mathbf{c}\]
(v) If m, n are scalars and \[\mathbf{a},\,\mathbf{b}\] be two vectors, then \[m\mathbf{a}\,.\,n\mathbf{b}=mn(\mathbf{a}\,.\,\mathbf{b})=(mn\,\mathbf{a})\,.\,\mathbf{b}=\mathbf{a}\,.\,(mn\,\mathbf{b})\]
(vi) For any vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have
(a) \[\mathbf{a}\,.\ (-\mathbf{b})=-(\mathbf{a}\,.\,\mathbf{b})=(-\mathbf{a})\,.\,\mathbf{b}\]
(b) \[(-\mathbf{a})\,.\,(-\mathbf{b})=\mathbf{a}\,.\,\mathbf{b}\]
(vii) For any two vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have
(a) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}+\ 2\mathbf{a}\,.\,\mathbf{b}\]
(b) \[|\mathbf{a}-\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}-\ 2\mathbf{a}\,.\,\mathbf{b}\]
(c) \[(\mathbf{a}+\mathbf{b})\,.\,(\mathbf{a}-\mathbf{b})=\ |\mathbf{a}{{|}^{2}}-|\mathbf{b}{{|}^{2}}\]
(d) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}|+|\mathbf{b}|\]\[\Rightarrow \] \[\mathbf{a}||\mathbf{b}\]
(e) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}\Rightarrow \mathbf{a}\bot \mathbf{b}\]
(f) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}-\mathbf{b}|\ \Rightarrow \mathbf{a}\bot \mathbf{b}\]
(3) Scalar product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\], then, \[\mathbf{a}\,.\,\mathbf{b}={{a}_{1}}{{b}_{1}}\] \[+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}\].
The components of \[\mathbf{b}\] along and perpendicular to \[\mathbf{a}\] are \[\left( \frac{\mathbf{a}\,.\ \mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] and \[\mathbf{b}-\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] respectively.
(4) Work done by a force :
Angle between two vectors : If \[\mathbf{a},\,\mathbf{b}\] be two vectors inclined at an angle \[\theta \], then \[\mathbf{a}\,.\,\mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\,\cos \theta \]
\[\Rightarrow \] \[\cos \theta =\frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|}\]\[\Rightarrow \] \[\theta ={{\cos }^{-1}}\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|} \right)\]
If \[\mathbf{a}\,={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\]; then
\[\theta ={{\cos }^{-1}}\left( \frac{{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}} \right)\].
(2) Properties of scalar product
(i) Commutativity : The scalar product of two vector is commutative i.e., \[\mathbf{a}\,.\,\mathbf{b}\,=\mathbf{b}\,.\,\mathbf{a}\].
(ii) Distributivity of scalar product over vector addition The scalar product of vectors is distributive over vector addition i.e., (a) \[\mathbf{a}\,.\,(\mathbf{b}\,+\mathbf{c})\,=\,\mathbf{a}\,.\,\mathbf{b}+\mathbf{a}\,.\,\mathbf{c}\], (Left distributivity)
(b) \[(\mathbf{b}+\mathbf{c})\,.\,\mathbf{a}=\mathbf{b}\,.\,\mathbf{a}+\mathbf{c}\,.\,\mathbf{a}\], (Right distributivity)
(iii) Let \[\mathbf{a}\] and \[\mathbf{b}\] be two non-zero vectors \[\mathbf{a}\,.\,\mathbf{b}=0\Leftrightarrow \mathbf{a}\bot \mathbf{b}\].
As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are mutually perpendicular unit vectors along the co-ordinate axes, therefore, \[\mathbf{i}\,.\,\mathbf{j}=\mathbf{j}\,.\,\mathbf{i}=0\]; \[\mathbf{j}\,.\,\mathbf{k}=\mathbf{k}\,.\,\mathbf{j}=0;\] \[\mathbf{k}\,.\,\mathbf{i}=\mathbf{i}\,.\,\mathbf{k}\,=0\].
(iv) For any vector \[\mathbf{a},\,\text{ }\mathbf{a}\,.\,\mathbf{a}=|\mathbf{a}{{|}^{2}}\].
As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are unit vectors along the co-ordinate axes, therefore \[\mathbf{i}\,.\,\mathbf{i}=|\mathbf{i}{{|}^{2}}=1\], \[\mathbf{j}\,.\,\mathbf{j}=|\mathbf{j}{{|}^{2}}=1\] and \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}+\mu \mathbf{c}\]
(v) If m, n are scalars and \[\mathbf{a},\,\mathbf{b}\] be two vectors, then \[m\mathbf{a}\,.\,n\mathbf{b}=mn(\mathbf{a}\,.\,\mathbf{b})=(mn\,\mathbf{a})\,.\,\mathbf{b}=\mathbf{a}\,.\,(mn\,\mathbf{b})\]
(vi) For any vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have
(a) \[\mathbf{a}\,.\ (-\mathbf{b})=-(\mathbf{a}\,.\,\mathbf{b})=(-\mathbf{a})\,.\,\mathbf{b}\]
(b) \[(-\mathbf{a})\,.\,(-\mathbf{b})=\mathbf{a}\,.\,\mathbf{b}\]
(vii) For any two vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have
(a) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}+\ 2\mathbf{a}\,.\,\mathbf{b}\]
(b) \[|\mathbf{a}-\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}-\ 2\mathbf{a}\,.\,\mathbf{b}\]
(c) \[(\mathbf{a}+\mathbf{b})\,.\,(\mathbf{a}-\mathbf{b})=\ |\mathbf{a}{{|}^{2}}-|\mathbf{b}{{|}^{2}}\]
(d) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}|+|\mathbf{b}|\]\[\Rightarrow \] \[\mathbf{a}||\mathbf{b}\]
(e) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}\Rightarrow \mathbf{a}\bot \mathbf{b}\]
(f) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}-\mathbf{b}|\ \Rightarrow \mathbf{a}\bot \mathbf{b}\]
(3) Scalar product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\], then, \[\mathbf{a}\,.\,\mathbf{b}={{a}_{1}}{{b}_{1}}\] \[+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}\].
The components of \[\mathbf{b}\] along and perpendicular to \[\mathbf{a}\] are \[\left( \frac{\mathbf{a}\,.\ \mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] and \[\mathbf{b}-\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] respectively.
(4) Work done by a force :
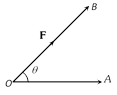 Work done \[=|\mathbf{F}|\,|\overrightarrow{OA}|\,\cos \theta =\mathbf{F}\,.\,\overrightarrow{OA}\,=\mathbf{F}\,.\mathbf{d}\], where \[\mathbf{d}=\overrightarrow{OA}\]
Work done = (Force). (Displacement)
If a number of forces are acting on a particle, then the sum of the works done by the separate forces is equal to the work done by the resultant force.
Work done \[=|\mathbf{F}|\,|\overrightarrow{OA}|\,\cos \theta =\mathbf{F}\,.\,\overrightarrow{OA}\,=\mathbf{F}\,.\mathbf{d}\], where \[\mathbf{d}=\overrightarrow{OA}\]
Work done = (Force). (Displacement)
If a number of forces are acting on a particle, then the sum of the works done by the separate forces is equal to the work done by the resultant force.
You need to login to perform this action.
You will be redirected in
3 sec
