question_answer 1)
Two springs of spring constants \[{{k}_{1}}\] and \[{{k}_{2}}\] are joined in series and a mass m is attached to them as shown in figure.
A)
\[T=\pi \sqrt{\frac{m({{k}_{1}}+{{k}_{2}})}{{{k}_{1}}{{k}_{2}}}}\]
done
clear
B)
\[T=2\pi \sqrt{\frac{m({{k}_{1}}+{{k}_{2}})}{{{k}_{1}}{{k}_{2}}}}\]
done
clear
C)
\[T=2\pi \sqrt{\frac{m}{{{k}_{1}}+{{k}_{2}}}}\]
done
clear
D)
\[T=2\pi \sqrt{\frac{m({{k}_{1}}+{{k}_{2}})}{2{{k}_{1}}{{k}_{2}}}}\]
done
clear
View Answer play_arrow
question_answer 2) A hot body at temperature T losses heat to the surrounding temperature \[{{T}_{S}}\] by radiation. If the difference in temperature is small then, the rate of loss of heat by the hot body is proportional to
A)
\[(T-{{T}_{S}})\]
done
clear
B)
\[{{(T-{{T}_{S}})}^{2}}\]
done
clear
C)
\[{{(T-{{T}_{S}})}^{1/2}}\]
done
clear
D)
\[{{(T-{{T}_{S}})}^{4}}\]
done
clear
View Answer play_arrow
question_answer 3) Which one of the following statement is not correct in the case of light emitting diodes?
A)
It is a heavily doped p-n junction
done
clear
B)
It emits light only when it is forward biased
done
clear
C)
It emits light only when it is reverse biased
done
clear
D)
The energy of the light emitted is less than the energy of the semiconductor used
done
clear
View Answer play_arrow
question_answer 4) Which one of the following cannot be used as a moderator in a nuclear reactor?
A)
Water
done
clear
B)
Heavy water
done
clear
C)
Molten sodium
done
clear
D)
Graphite
done
clear
View Answer play_arrow
question_answer 5) The fraction of a sample of radioactive nuclei that remains undecayed after one mean life is
A)
\[\frac{1}{e}\]
done
clear
B)
\[1-\frac{1}{e}\]
done
clear
C)
\[\frac{1}{{{e}^{2}}}\]
done
clear
D)
\[1-\frac{1}{{{e}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 6) If the radius of a nucleus of mass number 3 is R, ,then the radius of a nucleus of mass number 81 is
A)
\[3\,R\]
done
clear
B)
\[9\,R\]
done
clear
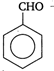
C)
\[{{(27)}^{1/2}}\,R\]
done
clear
D)
\[27\text{ }R\]
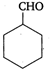
done
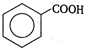
clear
View Answer play_arrow
question_answer 7) In hydrogen atom, which one of the following transitions is most energetic?
A)
\[{{n}_{1}}=2\to {{n}_{2}}=1\]
done
clear
B)
\[{{n}_{1}}=3\to {{n}_{2}}=1\]
done
clear
C)
\[{{n}_{1}}=10\to {{n}_{2}}=2\]
done
clear
D)
\[{{n}_{1}}=100\to {{n}_{2}}=3\]
done
clear
View Answer play_arrow
question_answer 8) A common example of \[{{\beta }^{-}}\] decay is \[_{15}{{P}^{32}}{{\to }_{17}}{{S}^{32}}+x+y\]. Then x and y stand for
A)
electron and neutrino
done
clear
B)
positron and neutrino
done
clear
C)
electron and antineutrino
done
clear
D)
positron and antineutrino
done
clear
View Answer play_arrow
question_answer 9) Based on the energy band description, a solid can be classified as insulator the energy gap between the valance band and conduction band is
A)
\[3\,\,eV<{{E}_{g}}<6\,eV\]
done
clear
B)
\[{{E}_{g}}>6\,eV\]
done
clear
C)
\[{{E}_{g}}<3\,eV\]
done
clear
D)
\[{{E}_{g}}=0\,eV\]
done
clear
View Answer play_arrow
question_answer 10)
In the diagram, a system of two metals of equal lengths and of same cross-sectional area are joined together.
A)
\[{{100}^{o}}C\]
done
clear
B)
\[{{125}^{o}}C\]
done
clear
C)
\[{{150}^{o}}C\]
done
clear
D)
\[{{200}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 11) A Carnot cycle has the reversible processes in the following order
A)
isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression
done
clear
B)
isothermal compression, adiabatic expansion, isothermal expansion and adiabatic compression
done
clear
C)
isothermal expansion, adiabatic compression, isothermal compression and adiabatic expansion
done
clear
D)
adiabatic expansion, isothermal expansion, adiabatic compression and isothermal compression
done
clear
View Answer play_arrow
question_answer 12) Through which mode of propagation, the radio waves can be sent from one place to another
A)
ground wave propagation
done
clear
B)
sky wave propagation
done
clear
C)
space wave propagation
done
clear
D)
All of them
done
clear
View Answer play_arrow
question_answer 13)
The logic operation carried out by the circuit below
A)
AND gate
done
clear
B)
OR gate
done
clear
C)
NOT gate
done
clear
D)
NAND gate
done
clear
View Answer play_arrow
question_answer 14) If \[\beta ,{{R}_{L}}\] and r are the AC current gain, load resistance and the input resistance of a transistor respectively in CE configuration, the voltage and the power gains respectively are
A)
\[\beta \frac{{{R}_{L}}}{r}\] and \[{{\beta }^{3}}\frac{{{R}_{L}}}{r}\]
done
clear
B)
\[\beta \frac{r}{{{R}_{L}}}\] and \[{{\beta }^{2}}\frac{r}{{{R}_{L}}}\]
done
clear
C)
\[\beta \frac{{{R}_{L}}}{r}\] and \[\beta {{\left( \frac{{{R}_{L}}}{r} \right)}^{2}}\]
done
clear
D)
\[\beta \frac{r}{{{R}_{L}}}\] and \[\beta {{\left( \frac{r}{{{R}_{L}}} \right)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 15) A message signal of frequency \[5\text{ }kHz\]and peak voltage \[10\text{ }V\]is used to amplify modulate a carrier wave with frequency \[1\text{ }MHz\]and peak voltage 20 V. The side bands produced are
A)
\[(1000\pm 5)kHz\]
done
clear
B)
\[(1000\pm 7.5)kHz\]
done
clear
C)
\[(1000\pm 10)kHz\]
done
clear
D)
\[(1000\pm 15)kHz\]
done
clear
View Answer play_arrow
question_answer 16) The volume of one mole of an ideal gas changes from V to \[2\text{ }V\]at temperature\[{{327}^{o}}C\] If R is the universal gas constant, then the work done in this process is
A)
\[300\text{ }R\]In 2
done
clear
B)
\[600\text{ }R\]In 2
done
clear
C)
\[300\]In 2
done
clear
D)
\[600\] In 2
done
clear
View Answer play_arrow
question_answer 17) A wooden piece can float both in mercury (of density\[13.6\text{ }g/cc\]) and in water (of density\[1\text{ }g/cc\]). The ratio of mass of mercury displaced to the mass of water displaced is
A)
\[1\]
done
clear
B)
\[13.6\]
done
clear
C)
\[\frac{1}{13.6}\]
done
clear
D)
\[\frac{12.6}{13.6}\]
done
clear
View Answer play_arrow
question_answer 18) A container of height 10 m which is open at the top, has water to its full height. Two small openings are made on the wall of the container .one exactly at the middle and the other at the bottom. The ratio of the velocities with which water comes out from the middle and the bottom region respectively is
A)
\[2\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[\frac{1}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 19) If the radius of a spherical liquid (of surface tension S) drop increases from r to \[r+Ar,\]the corresponding increase in the surface energy is
A)
\[8\pi \,r\,\Delta rS\]
done
clear
B)
\[4\pi \,r\,\Delta rS\]
done
clear
C)
\[16\pi \,r\,\Delta rS\]
done
clear
D)
\[2\pi \,r\,\Delta rS\]
done
clear
View Answer play_arrow
question_answer 20) Which one of the following is not an assumption in the kinetic theory of gases?
A)
The volume occupied by the molecules of the gas is negligible
done
clear
B)
The force of attraction between the molecules is negligible
done
clear
C)
The collision between molecules are elastic
done
clear
D)
All molecules have some speed
done
clear
View Answer play_arrow
question_answer 21) The crystal structure can be studied using
A)
UV rays
done
clear
B)
X-rays
done
clear
C)
IR radiation
done
clear
D)
Microwave
done
clear
View Answer play_arrow
question_answer 22) The number of turns of the primary and the secondary coils of a transformer are 10 and 100 respectively. The primary voltage and the current are given as \[2\text{ }V\]and\[1\text{ }A\]. Assuming the efficiency of the transformer as \[90%,\] the secondary voltage and the current respectively are
A)
\[20\text{ }V\]and\[0.1\text{ }A\]
done
clear
B)
\[0.2\text{ }V\]and \[1\text{ }A\]
done
clear
C)
\[20\,\,V\]and \[0.09\text{ }A\]
done
clear
D)
\[0.2\,\,V\]and \[0.9\text{ }A\]
done
clear
View Answer play_arrow
question_answer 23) Which one of the following units is not that of mutual inductance?
A)
Henry
done
clear
B)
Weber
done
clear
C)
Ohm-second
done
clear
D)
Volt-second-\[{{(ampere)}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 24) In an L-C-R series AC circuit at resonance
A)
the capacitive reactance is more than the inductive reactance
done
clear
B)
the capacitive reactance equals the inductive reactance
done
clear
C)
the capacitive reactance is less than the inductive reactance
done
clear
D)
the power dissipated is minimum
done
clear
View Answer play_arrow
question_answer 25) In an L-C-R serries resonant circuit which one of the following cannot be the expression for the Q-factor
A)
\[\frac{\omega L}{R}\]
done
clear
B)
\[\frac{1}{\omega \,\,CR}\]
done
clear
C)
\[\sqrt{\frac{L}{C}}\frac{1}{R}\]
done
clear
D)
\[\frac{R}{LC}\]
done
clear
View Answer play_arrow
question_answer 26) If the eighth bright band due to light of wavelength \[{{\lambda }_{1}}\] coincides with ninth bright band from light of wavelength \[{{\lambda }_{2}}\]in Young's double slit experiment, then the possible wavelengths of visible light are
A)
\[400\,\,nm\]and \[450\,\,nm\]
done
clear
B)
\[425\text{ }nm\] and \[400\text{ }nm\]
done
clear
C)
\[400\,\,nm\] and \[425\text{ }nm\]
done
clear
D)
\[450\,\,nm\] and \[400\,\,nm\]
done
clear
View Answer play_arrow
question_answer 27) The elastic energy stored per unit volume in a stretched wire is
A)
\[\frac{1}{2}\] (Young modulus) \[{{(Strain)}^{2}}\]
done
clear
B)
\[\frac{1}{2}\] (Stress) \[{{(Strain)}^{2}}\]
done
clear
C)
\[\frac{1}{2}\frac{Stress}{Strain}\]
done
clear
D)
\[\frac{1}{2}\] (Young modulus) (Stress)
done
clear
View Answer play_arrow
question_answer 28) The electromagnetic waves of frequency \[~2\text{ }MHz\]to \[30\text{ }MHz\]are used
A)
in ground wave propagation
done
clear
B)
in sky wave propagation
done
clear
C)
in microwave propagation
done
clear
D)
in satellite communication
done
clear
View Answer play_arrow
question_answer 29) Assuming that the earth is a sphere of radius \[{{R}_{E}}\]with uniform density, the distance from its centre at which the acceleration due to gravity is equal to \[\frac{g}{3}\] (g = the acceleration due to gravity on the surface of earth) is
A)
\[\frac{{{R}_{E}}}{3}\]
done
clear
B)
\[2\,\,\frac{{{R}_{E}}}{3}\]
done
clear
C)
\[\frac{{{R}_{E}}}{3}\]
done
clear
D)
\[\frac{{{R}_{E}}}{4}\]
done
clear
View Answer play_arrow
question_answer 30) The terminal velocity of a rain drop of radius r Is \[2\text{ }cm\,\,\,{{s}^{-1}}\]. If eight such identical drops combine to form a single large drop, the terminal velocity would be
A)
\[1\,cm\,\,\,{{s}^{-1}}\]
done
clear
B)
\[2\,cm\,\,\,{{s}^{-1}}\]
done
clear
C)
\[4\,cm\,\,\,{{s}^{-1}}\]
done
clear
D)
\[8\,cm\,\,\,{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 31) The maximum kinetic energy of photoelectrons
A)
varies linearly with the frequency of the incident radiation
done
clear
B)
, varies linearly with the wavelength of incident light
done
clear
C)
proportional to the frequency of the incident radiation
done
clear
D)
proportional to the square of the frequency of incident radiation
done
clear
View Answer play_arrow
question_answer 32) Which one of the following is not associated with the total internal reflection?
A)
The mirage formation
done
clear
B)
Optical fibre communication
done
clear
C)
The glittering of diamond
done
clear
D)
Dispersion of light
done
clear
View Answer play_arrow
question_answer 33) The angular width of the central maximum of the diffraction pattern in a single slit (of width a) experiment, with \[\lambda \] as the wavelength of light, is
A)
\[\frac{3\lambda }{2a}\]
done
clear
B)
\[\frac{\lambda }{2a}\]
done
clear
C)
\[\frac{2\lambda }{a}\]
done
clear
D)
\[\frac{\lambda }{a}\]
done
clear
View Answer play_arrow
question_answer 34) The Brewster angle for the glass-air interface is \[{{54.74}^{o}}\]. if a ray of light going from air to glass strikes at an angle of incidence \[{{45}^{o}},\] then the angle of refraction is (Given, tan\[{{54.74}^{o}}=\sqrt{2}\])
A)
\[{{60}^{o}}\]
done
clear
B)
\[{{30}^{o}}\]
done
clear
C)
\[{{25}^{o}}\]
done
clear
D)
\[{{54.74}^{o}}\]
done
clear
View Answer play_arrow
question_answer 35) When sun light is scattered by minute particles of atmosphere, the intensity of light scattered away is proportional to
A)
\[{{(wavelength\text{ }of\text{ }light)}^{4}}\]
done
clear
B)
\[{{(frequency\text{ }of\text{ }light)}^{4}}\]
done
clear
C)
\[{{(wavelength\text{ }of\text{ }light)}^{2}}\]
done
clear
D)
\[{{(frequency\text{ }of\text{ }light)}^{2}}\]
done
clear
View Answer play_arrow
question_answer 36) If K be the kinetic energy and m the mass of a moving particle, then the de-Broglie wavelength of the particle is
A)
\[\lambda =\frac{h}{\sqrt{mK}}\]
done
clear
B)
\[\lambda =\frac{2h}{\sqrt{mK}}\]
done
clear
C)
\[\lambda =\frac{h}{2\sqrt{mK}}\]
done
clear
D)
\[\lambda =\frac{h}{\sqrt{2\,mK}}\]
done
clear
View Answer play_arrow
question_answer 37) The radius of gyration of a thin uniform circular disc (of radius R) about an axis passing through its centre and lying in its plane is
A)
\[R\]
done
clear
B)
\[\frac{R}{\sqrt{2}}\]
done
clear
C)
\[\frac{R}{4}\]
done
clear
D)
\[\frac{R}{2}\]
done
clear
View Answer play_arrow
question_answer 38) Two particles of masses \[1\text{ }kg\]and \[\text{2 }kg\] are located at \[{{x}_{1}}=0,\] \[{{y}_{1}}=0\] and \[{{x}_{2}}=1,\]\[{{y}_{2}}=0\] respectively. The centre of mass of the system is at.
A)
\[x=1;\,\,y=2\]
done
clear
B)
\[x=2;\,\,y=1\]
done
clear
C)
\[x=\frac{1}{3};\,\,y=\frac{2}{3}\]
done
clear
D)
\[x=\frac{2}{3};\,\,y=\frac{1}{3}\]
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 39) The energy that is associated with one gram of mass is
A)
\[9\times {{10}^{-13}}\,J\]
done
clear
B)
\[9\times {{10}^{-16}}\,J\]
done
clear
C)
\[9\times {{10}^{13}}\,J\]
done
clear
D)
\[9\times {{10}^{16}}\,J\]
done
clear
View Answer play_arrow
question_answer 40) If the polar ice caps were to -melt suddenly
A)
the length of the day will be more than \[24\text{ }h\]
done
clear
B)
the length of the day will be less than \[24\text{ }h\]
done
clear
C)
the length of the day will remain as \[24\text{ }h\] the length of the day will become more
done
clear
D)
than \[24\text{ }h\] initially and then becomes equal to \[24\text{ }h\]
done
clear
View Answer play_arrow
question_answer 41) The work done in taking an object of mass m from the surface of earth to a height \[h=R,\] where R is the radius of the earth, is
A)
\[mgR\]
done
clear
B)
\[\frac{1}{2}mgR\]
done
clear
C)
\[\frac{1}{3}mgR\]
done
clear
D)
\[\frac{2}{3}mgR\]
done
clear
View Answer play_arrow
question_answer 42) The inversion temperature of a copper-iron thermocouple is \[{{540}^{o}}C\]when the cold junction temperature is \[{{0}^{o}}C\]. If the cold junction temperature is increased by\[{{10}^{o}}C,\] then the inversion temperature and the neutral temperature of the thermocouple respectively are
A)
\[{{270}^{o}}C\]and \[{{530}^{o}}C\]
done
clear
B)
\[{{270}^{o}}C\] and \[{{550}^{o}}C\]
done
clear
C)
\[{{280}^{o}}C\]and \[{{530}^{o}}C\]
done
clear
D)
\[{{280}^{o}}C\]and \[{{550}^{o}}C\]
done
clear
View Answer play_arrow
question_answer 43) Two bulbs marked \[60\text{ }W,\] \[220\text{ }V\] and \[100\text{ }W\]\[220\text{ }V\] are connected in series and the series combination is now connected across a \[220\text{ }V\] mains supply. The power dissipated in the circuit is
A)
\[37.5\text{ }W\]
done
clear
B)
\[75\text{ }W\]
done
clear
C)
\[80\text{ }W\]
done
clear
D)
\[40\text{ }W\]
done
clear
View Answer play_arrow
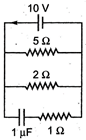
question_answer 44)
The steady state current through the battery in the circuit given below is
A)
\[17\,A\]
done
clear
B)
\[7\,A\]
done
clear
C)
zero
done
clear
D)
\[\frac{10}{7}A\]
done
clear
View Answer play_arrow
question_answer 45) Two concentric circular loops of radii R and 2R carry currents of 2i and i respectively in opposite sense (ie, clockwise in one coil and counter-clockwise in the other coil). The resultant magnetic field at their common centre is
A)
\[{{\mu }_{0}}\frac{i}{4R}\]
done
clear
B)
\[{{\mu }_{0}}\frac{5i}{4R}\]
done
clear
C)
\[{{\mu }_{0}}\frac{3i}{4R}\]
done
clear
D)
\[{{\mu }_{0}}\frac{i}{2R}\]
done
clear
View Answer play_arrow
question_answer 46)
Three identical spherical balls A, B and C are placed on a table as shown in the figure along a straight line. B and C are at rest initially.
A)
\[5\,m{{s}^{-1}}\]
done
clear
B)
\[10\,m{{s}^{-1}}\]
done
clear
C)
\[2.5\,m{{s}^{-1}}\]
done
clear
D)
\[7.5\,m{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 47) An object placed on an inclined plane starts sliding when the angle of incline becomes\[{{30}^{o}}\]. The coefficient of static friction between the object and the plane is
A)
\[\frac{1}{\sqrt{3}}\]
done
clear
B)
\[\sqrt{3}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[\frac{\sqrt{3}}{2}\]
done
clear
View Answer play_arrow
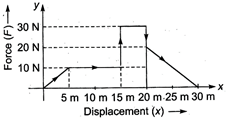
question_answer 48)
Given below is a graph between a variable force (F) (along y-axis) and the displacement (x) (along x-axis) of a particle in one dimension. The work done by the force in the displacement interval between \[0\text{ }m\]and \[30\text{ }m\]is
A)
\[275\text{ }J\]
done
clear
B)
\[375\text{ }J\]
done
clear
C)
\[400\text{ }J\]
done
clear
D)
\[300\text{ }J\]
done
clear
View Answer play_arrow
question_answer 49) The mobility of free electrons (charge = e, mass = -m and relaxation time = \[\tau \].) in a metal is proportional to
A)
\[\frac{e}{m}\tau \]
done
clear
B)
\[\frac{m}{e}\tau \]
done
clear
C)
\[\frac{e}{m\tau }\]
done
clear
D)
\[\frac{m}{e\tau }\]
done
clear
View Answer play_arrow
question_answer 50) n identical capacitors each of capacitance C when connected in parallel give the effective capacitance \[90\text{ }\mu F\]and when connected in series give \[\text{2}\text{.5 }\mu F\]. Then the values of n and C respectively are
A)
\[6\] and \[15\,\mu F\]
done
clear
B)
\[5\] and \[18\,\mu F\]
done
clear
C)
\[15\] and \[6\,\mu ,F\]
done
clear
D)
\[18\] and \[5\,\mu ,F\]
done
clear
View Answer play_arrow
question_answer 51) A capacitor is charged by a battery and the energy stored is U. The battery is now removed and the separation distance between the plates. is doubled. The energy stored now is
A)
\[\frac{U}{2}\]
done
clear
B)
\[U\]
done
clear
C)
\[2\,\,U\]
done
clear
D)
\[4\,\,U\]
done
clear
View Answer play_arrow
question_answer 52) The number of ways one can arrange three identical capacitors to obtain distinct effective capacitances is
A)
\[8\]
done
clear
B)
\[6\]
done
clear
C)
\[4\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 53) When a uniform wire of resistance R is stretched uniformly to increase its length by \[10%,\]the new resistance value would
A)
remain as R
done
clear
B)
become \[1.21R\]
done
clear
C)
become \[1.10\text{ }R\]
done
clear
D)
become \[1.20\text{ }R\]
done
clear
View Answer play_arrow
question_answer 54) Rocket propulsion is associated with
A)
the conservation of angular momentum
done
clear
B)
the conservation of mass
done
clear
C)
the conservation of mechanical energy
done
clear
D)
Newton's third law of motion
done
clear
View Answer play_arrow
question_answer 55) Which one of the following statements is not correct in uniform circular motion?
A)
The speed of the particle remains constant
done
clear
B)
The acceleration always points towards the centre
done
clear
C)
The angular speed remains constant
done
clear
D)
The velocity remains constant
done
clear
View Answer play_arrow
question_answer 56) If a car is to travel with a speed v along a frictionless, banked circular track of radius r, the required angle of banking so that the car does skid, is
A)
\[\theta ={{\tan }^{-1}}\,\left( \frac{{{v}^{2}}}{rg} \right)\]
done
clear
B)
\[\theta ={{\tan }^{-1}}\,\left( \frac{v}{rg} \right)\]
done
clear
C)
\[\theta ={{\tan }^{-1}}\,\left( \frac{{{r}^{2}}}{vg} \right)\]
done
clear
D)
\[\theta <{{\tan }^{-1}}\,\left( \frac{{{v}^{2}}}{rg} \right)\]
done
clear
View Answer play_arrow
question_answer 57) Three forces \[{{F}_{1}},{{F}_{2}}\] and \[{{F}_{3}}\] together keep a body in equilibrium. If \[{{F}_{1}}=3N\]along the positive x-axis, \[{{F}_{2}}=4N\] along the positive y-axis, then the third force \[{{F}_{3}}\] is
A)
\[5\text{ }N\]making an angle \[\theta ={{\tan }^{-1}}\left( \frac{3}{4} \right)\] with the negative y-axis
done
clear
B)
\[5\text{ }N\]making an angle \[\theta ={{\tan }^{-1}}\left( \frac{4}{3} \right)\] with the negative y-axis
done
clear
C)
\[7\text{ }N\]making an angle \[\theta ={{\tan }^{-1}}\left( \frac{3}{4} \right)\] with the negative y-axis
done
clear
D)
\[7\text{ }N\] making an angle \[\theta ={{\tan }^{-1}}\left( \frac{4}{3} \right)\] with the negative y-axis
done
clear
View Answer play_arrow
question_answer 58) The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre is
A)
\[\frac{Q}{4\,\pi \,{{\varepsilon }_{0}}r}\]for points outside and \[\frac{Q}{4\,\pi \,{{\varepsilon }_{0}}R}\] for points inside the shell
done
clear
B)
\[\frac{Q}{4\,\pi \,{{\varepsilon }_{0}}r}\] for both points inside and outside the shell
done
clear
C)
zero for points outside and \[\frac{Q}{4\,\pi \,{{\varepsilon }_{0}}r}\] for points inside the shell
done
clear
D)
zero for both points inside and outside the shell
done
clear
View Answer play_arrow
question_answer 59) The electric field and the potential of an electric dipole vary with distance r as
A)
\[\frac{1}{r}\]and \[\frac{1}{{{r}^{2}}}\]
done
clear
B)
\[\frac{1}{{{r}^{2}}}\] and \[\frac{1}{r}\]
done
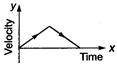
clear
C)
\[\frac{1}{{{r}^{2}}}\] and \[\frac{1}{{{r}^{3}}}\]
done
clear
D)
\[\frac{1}{{{r}^{3}}}\] and \[\frac{1}{{{r}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 60) A point charge Q is placed at one of the vertices of a cubical block. The electric flux flowing through this cube is
A)
\[\frac{Q}{6{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{Q}{4{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{Q}{8{{\varepsilon }_{0}}}\]
done
clear
D)
\[\frac{Q}{{{\varepsilon }_{0}}}\]
done
clear
View Answer play_arrow
question_answer 61) Two parallel infinite line charges \[+\lambda \] and \[-\lambda \] are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
A)
\[\frac{Q}{6\,{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{Q}{4\,{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{Q}{8\,{{\varepsilon }_{0}}}\]
done
clear
D)
\[\frac{Q}{\,{{\varepsilon }_{0}}}\]
done
clear
View Answer play_arrow
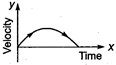
question_answer 62) A particle is thrown vertically up with a certain velocity. Assuming the air resistance to be negligible, which one of the following represents the velocity (along y-axis) time (along x-axis) graph for the entire motion of the particle till it reaches back to the ground
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 63) The dimensions of .the coefficient of viscosity are
A)
\[[M{{L}^{-1}}{{T}^{-3}}]\]
done
clear
B)
\[[M{{L}^{-1}}{{T}^{-1}}]\]
done
clear
C)
\[[M{{L}^{-2}}{{T}^{-1}}]\]
done
clear
D)
\[[ML{{T}^{-1}}]\]
done
clear
View Answer play_arrow
question_answer 64) The components of the sum of two vectors \[2\hat{i}+3\hat{j}\] and \[2\hat{j}+3\hat{k}\]along x and y directions respectively are
A)
\[2\] and \[5\]
done
clear
B)
\[4\]and \[6\]
done
clear
C)
\[2\] and \[6\]
done
clear
D)
\[4\]and \[3\]
done
clear
View Answer play_arrow
question_answer 65) An object is projected so that its horizontal range R is maximum. If the maximum height attained by the object is H, then the ratio of R/H is
A)
\[4\]
done
clear
B)
\[1/4\]
done
clear
C)
\[2\]
done
clear
D)
\[1/2\]
done
clear
View Answer play_arrow
question_answer 66) Which one of the following is not a characteristics of diamagnetism?
A)
The diamagnetic materials are repelled by a bar magnet
done
clear
B)
The magnetic susceptibility of the materials is small and negative
done
clear
C)
The origin of diamagnetism is the spin of electrons
done
clear
D)
The material move from a region of strong magnetic field to weak magnetic field
done
clear
View Answer play_arrow
question_answer 67) When the number of turns of the coil is doubled, the current sensitivity of a moving coil galvanometer is doubled whereas, the voltage sensitivity of the galvanometer
A)
remains the same
done
clear
B)
is halved
done
clear
C)
is doubled
done
clear
D)
is quadrupled
done
clear
View Answer play_arrow
question_answer 68) Ampere's circuital law is equivalent to
A)
Biot-Savart law
done
clear
B)
Coulomb's law
done
clear
C)
Faraday's law
done
clear
D)
Kirchhoff?s law
done
clear
View Answer play_arrow
question_answer 69) A proton, a deuteron and an alpha particle all having same momenta enter a uniform magnetic field and describe circular paths. The respective radii of their paths are in the ratio
A)
\[4:2:1\]
done
clear
B)
\[2:2:1\]
done
clear
C)
\[1:2:4\]
done
clear
D)
\[1:1:1\]
done
clear
View Answer play_arrow
question_answer 70) If the horizontal component of the earth's magnetic field is \[0.30\text{ }G,\] and the dip angle is \[60{}^\circ \] at a given place, then the value of earth's total magnetic field is
A)
\[0.15\text{ }G\]
done
clear
B)
\[0.15\,\sqrt{3}G\]
done
clear
C)
\[0.15\,\sqrt{2}G\]
done
clear
D)
\[~0.60\text{ }G\]
done
clear
View Answer play_arrow
question_answer 71) If a current of \[5\text{ }A\]in a coil of self inductance \[2\text{ }mH\]is cut-off in time \[0.1\text{ }s,\]the induced emf in the coil is
A)
\[0.1\,\,V\]
done
clear
B)
\[0.01\text{ }V\]
done
clear
C)
\[0.2V\]
done
clear
D)
\[0.02V\]
done
clear
View Answer play_arrow
question_answer 72) A source of sound is approaching an observer with speed of \[30\text{ }m{{s}^{-1}}\]and the observer is approaching the source with a speed of\[60\,\,m{{s}^{-1}}\]. Then the fractional change in the frequency of sound (speed of sound in air \[=330\,\,m{{s}^{-1}}\]) is
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{3}{10}\]
done
clear
C)
\[\frac{2}{5}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 73) A wave motion is described by \[y(x,t)=a\,\sin (kx-\omega t)\]. Then the ratio of the maximum particle velocity to the wave velocity is
A)
\[\omega a\]
done
clear
B)
\[\frac{1}{ka}\]
done
clear
C)
\[\frac{\omega }{k}\]
done
clear
D)
\[ka\]
done
clear
View Answer play_arrow
question_answer 74) The equation of a damped simple harmonic motion is \[m\frac{{{d}^{2}}x}{d{{t}^{2}}}+\frac{dx}{dt}+kx=0\]. Then the angular frequency of oscillation is
A)
\[\omega ={{\left( \frac{k}{m}-\frac{{{b}^{2}}}{4{{m}^{2}}} \right)}^{1/2}}\]
done
clear
B)
\[\omega ={{\left( \frac{k}{m}-\frac{b}{4m} \right)}^{1/2}}\]
done
clear
C)
\[\omega ={{\left( \frac{k}{m}-\frac{{{b}^{2}}}{4m} \right)}^{1/2}}\]
done
clear
D)
\[\omega ={{\left( \frac{k}{m}-\frac{{{b}^{2}}}{4{{m}^{2}}} \right)}^{1/2}}\]
done
clear
View Answer play_arrow
question_answer 75) The fundamental frequencies of an open and a closed tube, each of same length L with v as the speed of sound in air, respectively are
A)
\[\frac{v}{2L}\] and \[\frac{v}{L}\]
done
clear
B)
\[\frac{v}{L}\] and \[\frac{v}{2L}\]
done
clear
C)
\[\frac{v}{2L}\] and \[\frac{v}{4L}\]
done
clear
D)
\[\frac{v}{4L}\] and \[\frac{v}{2L}\]
done
clear
View Answer play_arrow
question_answer 76) For the reaction, \[{{N}_{2}}(g)+3{{H}_{2}}(g)\rightleftharpoons 2N{{H}_{3}}(g)\] at \[400\text{ }K,{{K}_{p}}=41.\] Find the value for the following reaction \[\frac{1}{2}{{N}_{2}}(g)+\frac{3}{2}{{H}_{2}}(g)\rightleftharpoons N{{H}_{3}}(g)\]
A)
6.4
done
clear
B)
0.02
done
clear
C)
50
done
clear
D)
4.6
done
clear
View Answer play_arrow
question_answer 77) What will be the resultant pH when 200 mL of, an aqueous solution of \[HCl(pH=2.0)\]is mixed with 300 mL of an aqueous solution of \[NaOH(pH=12)?\]
A)
2.699
done
clear
B)
13.30
done
clear
C)
11.3010
done
clear
D)
1.330
done
clear
View Answer play_arrow
question_answer 78) Why do most chemical reaction rates increases rapidly as the temperature rises?
A)
The fraction of the molecules with kinetic energy greater than the activation energy increases rapidly with temperature
done
clear
B)
The average kinetic energy increases as temperature rises
done
clear
C)
The activation energy decreases as the temperature rises
done
clear
D)
More collision take place between particles so that the reaction can occur
done
clear
View Answer play_arrow
question_answer 79) To an equilibrium mixture of \[2S{{O}_{2}}(g)+{{O}_{2}}(g)\rightleftharpoons 2S{{O}_{3}}(g),\] some helium, an inert gas, is added at constant volume. The addition of helium causes the total pressure to double, which of the following is true?
A)
The concentration of all three gases is unchanged
done
clear
B)
The concentration of sulphur trioxide increases
done
clear
C)
The number of moles of sulphur trioxide increases
done
clear
D)
The concentration of sulphur dioxide increases
done
clear
View Answer play_arrow
question_answer 80) Identify the substance whose 0.1 M solution is basic?
A)
Ammonium chloride
done
clear
B)
Ammonium acetate
done
clear
C)
Ammonium sulphate
done
clear
D)
Sodium acetate
done
clear
View Answer play_arrow
question_answer 81) The vapour pressure of pure liquid solvent is 0.80 arm. When a non-volatile substance B is added to the solvent, its vapour pressure drops to 0.6 arm. What is the mole fraction of component B in this solution?
A)
0.75
done
clear
B)
0.25
done
clear
C)
0.48
done
clear
D)
0.3
done
clear
View Answer play_arrow
question_answer 82) The standard enthalpy of formation of\[{{\text{H}}_{\text{2}}}\text{(g)}\] and\[C{{l}_{2}}(g)\]and\[HCl(g)\]are \[218\text{ }kJ/mol,\]\[\text{ }121.68\text{ }kJ/mol\]and\[92.31\text{ }kJ/mol\]respectively. Calculate standard enthalpy change in kJ for \[\frac{1}{2}{{H}_{2}}(g)\frac{1}{2}C{{l}_{2}}(g)\xrightarrow{{}}HCl(g)\]
A)
\[+\,\,431.99\]
done
clear
B)
\[-246.37\]
done
clear
C)
\[-431.99\]
done
clear
D)
\[+\,247.37\]
done
clear
E)
None of these
done
clear
View Answer play_arrow
question_answer 83) In which of the following pair the enthalpy of neutralization does not remain constant?
A)
\[\text{HN}{{\text{O}}_{\text{3}}}\]and\[\text{ }\!\!~\!\!\text{ NaOH}\]
done
clear
B)
\[HCl\]and \[NaOH\]
done
clear
C)
\[HCN\]and \[NaOH\]
done
clear
D)
\[{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\] and \[NaOH\]
done
clear
View Answer play_arrow
question_answer 84) A system is changed from an initial state to a final state by a manner such that \[\Delta H=q.\]If the change from the initial state to the final state were made by a different manner then \[\Delta H\]remains same but q changes because
A)
\[\Delta H\] is a path function and q is a state function
done
clear
B)
\[\Delta H\]is a state function and q is a path function
done
clear
C)
Both \[\Delta H\]and q are state function
done
clear
D)
Both \[\Delta H\]and q are path function
done
clear
View Answer play_arrow
question_answer 85) When water is cooled to ice, its entropy
A)
increases
done
clear
B)
decreases
done
clear
C)
remains same
done
clear
D)
becomes zero
done
clear
View Answer play_arrow
question_answer 86) The charge on \[\text{Fe(OH}{{\text{)}}_{\text{3}}}\]sol is due to
A)
adsorption of hydroxyl ion
done
clear
B)
adsorption of hydrogen ion
done
clear
C)
adsorption of ferric ion
done
clear
D)
absorption of ferric ion
done
clear
View Answer play_arrow
question_answer 87) Which of the following statement is true?
A)
Chemisorption forms multimolecular layer
done
clear
B)
Chemisorption is a reversible process
done
clear
C)
Chemisorption is independent of the pressure
done
clear
D)
Chemisorption has low enthalpy change
done
clear
View Answer play_arrow
question_answer 88) Identify the incorrect statement out of the following.
A)
Isoelectronic species have dissimilar ionic radii
done
clear
B)
Be and Al does not show diagonal relationship
done
clear
C)
Outer electronic configuration of halogen is \[n{{s}^{2}}.n{{p}^{7}}\]
done
clear
D)
In any period atomic radius of noble gas is the highest
done
clear
View Answer play_arrow
question_answer 89) According to VSEPR theory, the molecule that has T-shape is
A)
\[Cl{{F}_{3}}\]
done
clear
B)
\[N{{H}_{3}}\]
done
clear
C)
\[B{{F}_{3}}\]
done
clear
D)
\[{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 90) Bakelite is the polymer of
A)
benzaldehyde and phenol
done
clear
B)
formaldehyde and phenol
done
clear
C)
formaldehyde and benzyl alcohol
done
clear
D)
acetaldehyde and phenol
done
clear
View Answer play_arrow
question_answer 91) Which of these elements is expected to have the lowest first ionisation potential?
A)
Sr
done
clear
B)
As
done
clear
C)
Xe
done
clear
D)
S
done
clear
View Answer play_arrow
question_answer 92) Which is false statement about LCAO?
A)
Addition of atomic orbital results in molecular orbital
done
clear
B)
Atomic orbital of nearly same energy combine to molecular orbital
done
clear
C)
Bonding molecular orbital occupies higher energy than the atomic orbitals
done
clear
D)
Each molecular orbital accommodate maximum of two electrons
done
clear
View Answer play_arrow
question_answer 93) Which one among the following statement about transition elements is incorrect?
A)
They show variable oxidation state
done
clear
B)
All the ions are coloured
done
clear
C)
They exhibit diamagnetic and paramagnetic properties
done
clear
D)
They exhibit catalytic properties
done
clear
View Answer play_arrow
question_answer 94) German silver is an alloy of
A)
copper, zinc and silver
done
clear
B)
copper, zinc and nickel
done
clear
C)
copper, zinc and tin
done
clear
D)
manganese, chromium and nickel
done
clear
View Answer play_arrow
question_answer 95) The metal-carbon bond in metal carbonyls possess
A)
only s character
done
clear
B)
only p character
done
clear
C)
both s and p character
done
clear
D)
only d character
done
clear
View Answer play_arrow
question_answer 96) Irregular trend in the standard reduction potential value of first row transition elements is due to
A)
regular variation of first and second ionisation enthalpies
done
clear
B)
irregular variation of sublimation enthalpies
done
clear
C)
regular variation of sublimation enthalpies
done
clear
D)
increase in the number of unpaired electrons
done
clear
View Answer play_arrow
question_answer 97) Which of the following lanthanoid ion is paramagnetic?
A)
\[C{{e}^{4+}}\]
done
clear
B)
\[Y{{b}^{2+}}\]
done
clear
C)
\[L{{u}^{3+}}\]
done
clear
D)
\[E{{u}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 98) The complex \[{{[Co{{F}_{6}}]}^{4-}}\] is
A)
outer orbital and diamagnetic
done
clear
B)
inner orbital and paramagnetic
done
clear
C)
inner orbital and diamagnetic
done
clear
D)
outer orbital and paramagnetic
done
clear
View Answer play_arrow
question_answer 99) The oxidation number, d-orbital occupation and coordination number of Cr in the complex \[cis[Cr{{(en)}_{2}}C{{l}_{2}}]Cl\]are respectively
A)
\[+\,3,\text{ }3d\]and 4
done
clear
B)
\[~+\,3,\text{ }4d\] and 6
done
clear
C)
\[+\,3,\text{ }3d\]and 6
done
clear
D)
\[~+\,2,\text{ }3d\] and 6
done
clear
View Answer play_arrow
question_answer 100) Which is a non-aromatic compound?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 101) The number of isomers including stereoisomers possible for the compound having molecular formula \[{{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}\]is
A)
one
done
clear
B)
two
done
clear
C)
three
done
clear
D)
four
done
clear
View Answer play_arrow
question_answer 102) The correct order of decreasing acidic nature of \[Hp,\text{ }ROH,CH\equiv CH\]and\[N{{H}_{3}}\] is
A)
\[CH\equiv CH>{{H}_{2}}O>ROH>N{{H}_{3}}\]
done
clear
B)
\[{{H}_{2}}O\,>ROH>CH\equiv CH>N{{H}_{3}}\]
done
clear
C)
\[ROH>N{{H}_{3}}>CH\equiv CH>{{H}_{2}}O\]
done
clear
D)
\[{{H}_{2}}O>ROH>N{{H}_{3}}>CH\equiv CH\]
done
clear
View Answer play_arrow
question_answer 103) Reaction between propene and hydrochloric acid to form \[iso-\]propyl chloride takes place through
A)
nucleophilic addition reaction
done
clear
B)
electrophilic substitution reaction
done
clear
C)
nucleophilic substitution reaction
done
clear
D)
electrophilic addition reaction
done
clear
View Answer play_arrow
question_answer 104) Stability of\[iso-\]butylene can be best explained by
A)
inductive effect
done
clear
B)
mesomeric effect
done
clear
C)
hyperconjugative effect
done
clear
D)
steric effect
done
clear
View Answer play_arrow
question_answer 105) The d and I enantiomers of an optically active compound differ in
A)
their boiling and melting point
done
clear
B)
their rotation of plane polarized light
done
clear
C)
their solubility
done
clear
D)
their refractive index
done
clear
View Answer play_arrow
question_answer 106) Cannizaro reaction is not given by
A)
methanal
done
clear
B)
phenyl methanal
done
clear
C)
2, 2-dimethyl butanal
done
clear
D)
phenyl ethanol
done
clear
View Answer play_arrow
question_answer 107) Which of the following compound will have the smallest \[\text{p}{{\text{K}}_{\text{a}}}\]value?
A)
Benzoic acid
done
clear
B)
Formic acid
done
clear
C)
Acetic acid
done
clear
D)
Phenyl acetic acid
done
clear
View Answer play_arrow
question_answer 108) Ethyl alcohol cannot be used as a solvent for methyl magnesium iodide because
A)
methyl magnesium iodide reacts with alcohol-giving methane
done
clear
B)
the reaction between them is explosive in nature
done
clear
C)
methyl magnesium iodide is converted to ethyl magnesium iodide
done
clear
D)
alcohol is immiscible with methyl magnesium iodide
done
clear
View Answer play_arrow
question_answer 109) Which is not true about acetophenone?
A)
It reacts with alkaline potassium permanganate followed by acid hydrolysis and forms benzoic acid
done
clear
B)
It reacts with iodine and sodium hydroxide to form tri-iodomethane
done
clear
C)
It is prepared by the reaction of benzene with benzoyl chloride in presence of anhydrous aluminium chloride
done
clear
D)
It does not react with freshly prepared ammoniacal silver nitrate solution
done
clear
View Answer play_arrow
question_answer 110) Formation of methyl tertiary butyl ether by the reaction of sodium tertiary butoxide and methyl bromide involves
A)
elimination reaction
done
clear
B)
electrophilic addition reaction
done
clear
C)
nucleophilic substitution unimolecular reaction
done
clear
D)
nucleophilic substitution bimolecular reaction
done
clear
View Answer play_arrow
question_answer 111) 10 g of a radioisotope is reduced to 1.25 g of . active material after 12 yr. Therefore, the half-life of the isotope (in yr) is
A)
24
done
clear
B)
4
done
clear
C)
2
done
clear
D)
8
done
clear
View Answer play_arrow
question_answer 112) Out of the following, which is the correct set of quantum number for the outermost electron of potassium atom (Z = 19)?
A)
\[n-4\] \[l-3\] \[m-2\] \[s-\,\,\,\,\,\text{-1/2}\]
done
clear
B)
\[n-4\] \[l-2\] \[m-0\] \[s-\,\,\,\,\,\text{-1/2}\]
done
clear
C)
\[n-4\] \[l-1\] \[m-0\] \[s-\,\,\,\,\,+\text{1/2}\]
done
clear
D)
\[n-4\] \[l-0\] \[m-0\] \[s-\,\,\,\,\,\text{-1/2}\]
done
clear
View Answer play_arrow
question_answer 113) The molecules present in 5.6 L of sulphur dioxide at STP is
A)
\[1.5\times {{10}^{23}}\]
done
clear
B)
\[1.5\times {{10}^{-23}}\]
done
clear
C)
\[4\times {{10}^{23}}\]
done
clear
D)
\[0.15\times {{10}^{23}}\]
done
clear
View Answer play_arrow
question_answer 114) What is the relationship between the parent and daughter nuclei, when a nucleus of an atom undergoes beta emission?
A)
Isobars
done
clear
B)
Isotopes
done
clear
C)
Isotones
done
clear
D)
Isomers
done
clear
View Answer play_arrow
question_answer 115) In photoelectric effect, the kinetic energy of the photoelectron increases linearly with the
A)
wavelength of the incident light
done
clear
B)
frequency of the incident light
done
clear
C)
velocity of the incident light
done
clear
D)
atomic mass of an element
done
clear
View Answer play_arrow
question_answer 116) Dual behaviour of matter was proposed by
A)
Niels Bohr
done
clear
B)
Erwin Schrodinger
done
clear
C)
Louis de-Broglie
done
clear
D)
Max Planck
done
clear
View Answer play_arrow
question_answer 117) What is the maximum number of emission lines obtained when the excited electron of a hydrogen atom in \[n=5\]drops to the ground state?
A)
10
done
clear
B)
5
done
clear
C)
12
done
clear
D)
15
done
clear
View Answer play_arrow
question_answer 118) For a reaction\[[R]\xrightarrow{{}}P\]a graph of [R] against time is found to be a straight line. What is the order of this reaction?
A)
Second order
done
clear
B)
Third order
done
clear
C)
First order
done
clear
D)
Zero order
done
clear
View Answer play_arrow
question_answer 119) For getting accurate value of molar mass of a solute by osmotic pressure measurement
A)
the solute must be volatile
done
clear
B)
the solution concentration must be high
done
clear
C)
the solute should undergo dissociation
done
clear
D)
the solute must be non-volatile
done
clear
View Answer play_arrow
question_answer 120) In a catalytic experiment involving the Haber process, \[{{N}_{2}}(g)+3{{H}_{2}}(g)\xrightarrow{{}}2N{{H}_{3}}(g),\] the rate of reaction was measured as Rate \[=[N{{H}_{3}}]=2.0\times {{10}^{-4}}M{{s}^{-1}}\] If there were no side reactions what was the rate of reaction expressed in terms of \[{{N}_{2}}?\]
A)
\[1\times {{10}^{-4}}M{{s}^{-1}}\]
done
clear
B)
\[4\times {{10}^{-4}}M{{s}^{-1}}\]
done
clear
C)
\[5\times {{10}^{-3}}M{{s}^{-1}}\]
done
clear
D)
\[1\times {{10}^{-3}}M{{s}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 121) For a dilute solution, Raoulfs law states that
A)
lowering of vapour pressure is equal to the mole fraction of the solute
done
clear
B)
relative lowering of vapour pressure is equal to the mole fraction of the solvent
done
clear
C)
relative lowering of vapour pressure of the solvent is equal to the mole fraction of the solute
done
clear
D)
vapour pressure of the solution is equal to the vapour pressure of the solvent
done
clear
View Answer play_arrow
question_answer 122) 36 g of glucose (molar mass\[=180\text{ }g/mol\]) if present in 500 g of water, the molality of the solution is
A)
0.2
done
clear
B)
0.4
done
clear
C)
0.8
done
clear
D)
1.0
done
clear
View Answer play_arrow
question_answer 123) A certain current liberates 0.504 g hydrogen is 2 h. How many gram of oxygen can be liberated by the same current in the same time?
A)
2.0 g
done
clear
B)
0.4 g
done
clear
C)
4.0 g
done
clear
D)
8.0 g
done
clear
View Answer play_arrow
question_answer 124) The reduction potential values of X, Y and Z are \[-3.05\,V,-0.44\,V\]and\[~-0.83\,V\] respectively. Which of the following order is correct with respect to their reducing property?
A)
\[X>Y>Z\]
done
clear
B)
\[X>Z>Y\]
done
clear
C)
\[Y>Z>X\]
done
clear
D)
\[~Z>Y>X\]
done
clear
View Answer play_arrow
question_answer 125) Relationship between atomic radius r and the edge length a of a body centred cubic unit cell is
A)
\[r=\frac{a}{2}\]
done
clear
B)
\[r=\sqrt{\frac{a}{2}}\]
done
clear
C)
\[r=\frac{\sqrt{3}}{4}a\]
done
clear
D)
\[r=\frac{3a}{2}\]
done
clear
View Answer play_arrow
question_answer 126) Calculate the reduction potential of a half-cell containing of platinum electrode immersed in \[\text{2}\text{.0}\,\text{M}\,\text{F}{{\text{e}}^{\text{2+}}}\]and \[\text{0}\text{.02 M F}{{\text{e}}^{\text{3+}}}\text{.}\] Given \[\text{E}_{F{{e}^{3+}}/F{{e}^{2+}}}^{o}=0.771\,V,\] \[F{{e}^{3+}}+{{e}^{-}}\xrightarrow{{}}F{{e}^{2+}}\]
A)
0.653 V
done
clear
B)
0.889 V
done
clear
C)
0.0653V
done
clear
D)
2.771V
done
clear
View Answer play_arrow
question_answer 127) Faraday constant is defined as
A)
charge carried by one electron
done
clear
B)
charge carried by one mole of electron
done
clear
C)
charge required depositing one mole of substance
done
clear
D)
charge carried by two moles of electron
done
clear
View Answer play_arrow
question_answer 128) If 300mL of a gas weighs 0.368 g at STP. What is its molecular weight?
A)
30.16
done
clear
B)
2.55
done
clear
C)
27.5
done
clear
D)
37.5
done
clear
View Answer play_arrow
question_answer 129) Which one of the following compound exhibit both Schottky and Frenkel defects?
A)
\[~NaCl\]
done
clear
B)
\[~AgCl\]
done
clear
C)
\[AgBr\]
done
clear
D)
\[Agl\]
done
clear
View Answer play_arrow
question_answer 130) Identify the molecule that has zero dipole moment.
A)
\[C{{H}_{3}}Cl\]
done
clear
B)
\[CHC{{l}_{3}}\]
done
clear
C)
\[C{{H}_{2}}C{{l}_{2}}\]
done
clear
D)
\[CC{{l}_{4}}\]
done
clear
View Answer play_arrow
question_answer 131) Which one statement about sulphur dioxide gas is incorrect?
A)
It has an angular shape
done
clear
B)
lt decolourises acidified potassium permanganate solution
done
clear
C)
Two S?O bonds are equal
done
clear
D)
It is a dehydrating agent
done
clear
View Answer play_arrow
question_answer 132) In which of the following arrangement, the order is not according to the property indicated against it?
A)
\[{{F}_{2}}>C{{l}_{2}}>B{{r}_{2}}>{{I}_{2}}-\]Oxidising agent
done
clear
B)
\[N{{H}_{3}}>P{{H}_{3}}>As{{H}_{3}}>Sb{{H}_{3}}>Bi{{H}_{3}}-\]Basic property
done
clear
C)
\[F>Cl>Br>I-\]Electron gain enthalpy
done
clear
D)
\[C>Si>Ge>Sn-\]Ability to form p-p bond
done
clear
View Answer play_arrow
question_answer 133) In \[\text{C}{{\text{O}}_{\text{2}}}\text{,C}{{\text{H}}_{\text{4}}}\]and\[\text{CH}_{\text{3}}^{\text{+}}\]the hybridisation of carbon atom are
A)
\[s{{p}^{2}},s{{p}^{3}}\]and \[s{{p}^{2}}\]respectively
done
clear
B)
\[~sp,s{{p}^{3}}\] and \[s{{p}^{2}}\]respectively
done
clear
C)
\[~sp,\text{ }s{{p}^{3}}\] and \[sp\]respectively
done
clear
D)
\[s{{p}^{2}},\text{ }s{{p}^{3}}\]and \[sp\]respectively
done
clear
View Answer play_arrow
question_answer 134) Why calcium ion makes water hard but sodium ion does not?
A)
Calcium forms insoluble compound with stearate ion present in soap
done
clear
B)
Sodium forms insoluble compound with stearate ion present in soap
done
clear
C)
Calcium forms soluble compound with stearate ion present in soap
done
clear
D)
Both calcium and sodium forms insoluble compound with stearate ion present in soap
done
clear
View Answer play_arrow
question_answer 135) The colourless gas that turns brown in air is
A)
\[NO\]
done
clear
B)
\[N{{O}_{2}}\]
done
clear
C)
\[{{N}_{2}}{{O}_{4}}\]
done
clear
D)
\[{{N}_{2}}{{O}_{5}}\]
done
clear
View Answer play_arrow
question_answer 136) IUPAC name of the complex \[{{K}_{3}}[Al{{({{C}_{2}}{{O}_{4}})}_{3}}]\]is
A)
potassium tris(oxalato)aluminate(III)
done
clear
B)
potassium tri(oxalato)aluminate(III)
done
clear
C)
potassium tris(oxalato)aluminium(III)
done
clear
D)
potassium tri(oxalato)alumimum(III)
done
clear
View Answer play_arrow
question_answer 137) The depressant used to separate lead sulphide and zinc sulphide ores is
A)
potassium cyanide
done
clear
B)
sodium cyanide
done
clear
C)
silver cyanide
done
clear
D)
sodium sulphide
done
clear
View Answer play_arrow
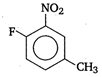
question_answer 138)
IUPAC name of the compound
A)
1-fluoro-4-methyl-2-nitrobenzene
done
clear
B)
4-fluoro-1-methyl-3-nitrobenzene
done
clear
C)
4-methyl-1-fluoro-2-nitrobenzene
done
clear
D)
5-methyl-2-fluoro-1-nitrobenzene
done
clear
View Answer play_arrow
question_answer 139) In the extraction of copper, the copper matte is a mixture of
A)
copper(II) sulphide and iron(II) sulphide
done
clear
B)
copperd (II) sulphide and iron(III) sulphide
done
clear
C)
copper(I) sulphide and iron(II) sulphide
done
clear
D)
copper(I) sulphide and iron(III) sulphide
done
clear
View Answer play_arrow
question_answer 140) Silver halide which is readily soluble m ammonium chloride is
A)
silver chloride
done
clear
B)
silver bromide
done
clear
C)
silver fluoride
done
clear
D)
silver iodide
done
clear
View Answer play_arrow
question_answer 141) Which of the following reagent can be used to convert ethanamide to methanamme?
A)
\[{{P}_{2}}{{O}_{5}}\]
done
clear
B)
\[NaOBr\]
done
clear
C)
\[LiAl{{H}_{4}}/{{H}_{2}}O\]
done
clear
D)
\[Na(Hg)/{{C}_{2}}{{H}_{5}}OH\]
done
clear
View Answer play_arrow
question_answer 142) Identify the product ?C? in the series \[{{C}_{6}}{{H}_{5}}N{{O}_{2}}\xrightarrow{Fe/HCl}A\xrightarrow[273\,K]{NaN{{O}_{2}}+HCl}\]\[B\xrightarrow[283\,K]{{{H}_{2}}O}C\]
A)
\[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}\text{OH}\]
done
clear
B)
\[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}\text{C}{{\text{H}}_{\text{2}}}\text{OH}\]
done
clear
C)
\[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}\text{CHO}\]
done
clear
D)
\[{{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}\text{N}{{\text{H}}_{\text{2}}}\]
done
clear
View Answer play_arrow
question_answer 143) The class of drug used for the treatment of stress is
A)
analgesics
done
clear
B)
antiseptic
done
clear
C)
antihistamine
done
clear
D)
tranquilizers
done
clear
View Answer play_arrow
question_answer 144) Compound that has smell of bitter almonds is
A)
aniline
done
clear
B)
benzonitnie
done
clear
C)
phenylisocyanide
done
clear
D)
nitrobenzene
done
clear
View Answer play_arrow
question_answer 145) Which of the following is the correct increasing order of basicity of amines in gaseous phase?
A)
\[{{(C{{H}_{3}})}_{2}}NH>C{{H}_{3}}N{{H}_{2}}>{{(C{{H}_{3}})}_{3}}N>N{{H}_{3}}\]
done
clear
B)
\[{{(C{{H}_{3}})}_{3}}N>{{(C{{H}_{3}})}_{2}}NH>C{{H}_{3}}N{{H}_{2}}>N{{H}_{3}}\]
done
clear
C)
\[{{(C{{H}_{3}})}_{2}}NH>{{(C{{H}_{3}})}_{3}}N>C{{H}_{3}}N{{H}_{2}}>N{{H}_{3}}\]
done
clear
D)
\[{{(C{{H}_{3}})}_{3}}N>C{{H}_{3}}N{{H}_{2}}>{{(C{{H}_{3}})}_{2}}NH>N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 146) Nitrogenous base that found in RNA but absent in DNA is
A)
uracil
done
clear
B)
thymine
done
clear
C)
cytosine
done
clear
D)
adenine
done
clear
View Answer play_arrow
question_answer 147) Glycerol when reacts with potassium hydrogen sulphate at \[473\text{ }K-503\text{ }K\]forms
A)
allyl iodide
done
clear
B)
allyl alcohol
done
clear
C)
glycericacid
done
clear
D)
acrolein
done
clear
View Answer play_arrow
question_answer 148) Phenol reacts with bromine in chloroform at low temperature to give
A)
\[m-\]bromophenol
done
clear
B)
mixture of ortho and para bromophenol
done
clear
C)
\[~p-\] bromophenol
done
clear
D)
2, 4, 6-tribromophenol
done
clear
View Answer play_arrow
question_answer 149)
Identify the compound 'X' in the following reaction
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 150) Alkyl halides undergoing substitution nucleophilic bimolecular reaction involves
A)
formation of carbocation
done
clear
B)
racemic mixture
done
clear
C)
inversion of configuration
done
clear
D)
retention of configuration
done
clear
View Answer play_arrow
question_answer 151) The radius of the sphere \[|\,3\,\vec{r}+2\hat{i}-\hat{j}-4\hat{k}|=3\] is
A)
\[2\]
done
clear
B)
\[3\]
done
clear
C)
\[1\]
done
clear
D)
\[9\]
done
clear
View Answer play_arrow
question_answer 152) The foot of the perpendicular drawn from the origin to a plane is \[(1,-1,5)\]. The equation of the plane is
A)
\[\vec{r}.(\hat{i}-\hat{j}+5\hat{k})=27\]
done
clear
B)
\[\vec{r}.(\hat{i}-\hat{j}+5\hat{k})=\sqrt{27}\]
done
clear
C)
\[\vec{r}.(5\hat{i}-\hat{j}+\hat{k})=\frac{1}{\sqrt{27}}\]
done
clear
D)
\[x-y-5z-27=0\]
done
clear
View Answer play_arrow
question_answer 153) The dual of the statement \[(\tilde{\ }p)\wedge [(\tilde{\ }q)\wedge (p\vee q)\wedge (\tilde{\ }r)]\]is
A)
\[p\wedge [q\vee (p\wedge q)\vee r]\]
done
clear
B)
\[(\tilde{\ }p)\vee [(\tilde{\ }q)\vee (p\wedge q)\vee (\tilde{\ }r)]\]
done
clear
C)
\[(\tilde{\ }p)\wedge [(\tilde{\ }q)\vee (p\vee q)\vee r]\]
done
clear
D)
\[(\tilde{\ }p)\vee [(\tilde{\ }q)\vee (p\wedge q)\vee r]\]
done
clear
View Answer play_arrow
question_answer 154) The vector equation of the straight line \[6x-8=2y-7=3z\]is
A)
\[\vec{r}=\left( \frac{8}{6}\hat{i}+\frac{7}{2}\hat{j} \right)+t\left( \frac{1}{6}\hat{i}+\frac{1}{2}\hat{j}-\frac{1}{3}\hat{k} \right)\]
done
clear
B)
\[\vec{r}=\left( \frac{8}{6}\hat{i}+\frac{7}{2}\hat{j} \right)+s\left( \frac{1}{6}\hat{i}+\frac{1}{2}\hat{j}-\frac{1}{3}\hat{k} \right)\]
done
clear
C)
\[\vec{r}=\left( -\frac{8}{6}\hat{i}-\frac{7}{2}\hat{j} \right)+t\left( \frac{1}{6}\hat{i}+\frac{1}{2}\hat{j}-\frac{1}{3}\hat{k} \right)\]
done
clear
D)
\[\vec{r}=\left( -\frac{8}{6}\hat{i}-\frac{7}{2}\hat{j} \right)+s\left( \frac{1}{6}\hat{i}-\frac{1}{2}\hat{j}-\frac{1}{3}\hat{k} \right)\]
done
clear
View Answer play_arrow
question_answer 155) The unit normal vector to the plane \[3x+2y-2z=8\sqrt{17}\] is
A)
\[\frac{1}{\sqrt{3}}\,(\hat{i}+\hat{j}-\hat{k})\]
done
clear
B)
\[\frac{1}{\sqrt{17}}\,(3\hat{i}+2\hat{j}-2\hat{k})\]
done
clear
C)
\[\frac{1}{\sqrt{13}}\,(3\hat{i}+2\hat{j}+2\hat{k})\]
done
clear
D)
\[\frac{1}{\sqrt{11}}\,(3\hat{i}+\hat{j}+\hat{k})\]
done
clear
View Answer play_arrow
question_answer 156) The centroid of the triangle formed by joining the mid points of the sides of a triangle with vertices \[(-1,-1),(2,4)\] and \[(-5,-6)\] is
A)
\[\left( -\frac{2}{3},1 \right)\]
done
clear
B)
\[\left( -\frac{4}{3},-1 \right)\]
done
clear
C)
\[\left( -\frac{1}{3},\frac{1}{2} \right)\]
done
clear
D)
\[\left( -\frac{1}{4},\frac{1}{4} \right)\]
done
clear
View Answer play_arrow
question_answer 157) if the straight lines \[2x+5ay-1=0\] and \[3x+7y+7=0\] are mutually perpendicular, then value of \[\alpha \] is
A)
\[\frac{6}{37}\]
done
clear
B)
\[\frac{-6}{31}\]
done
clear
C)
\[\frac{-6}{37}\]
done
clear
D)
\[\frac{-6}{35}\]
done
clear
View Answer play_arrow
question_answer 158) The pair of straight lines \[{{x}^{2}}-3{{y}^{2}}=0\]and the line \[x=1\]form a triangle which is
A)
right angled
done
clear
B)
isosceles
done
clear
C)
scalene
done
clear
D)
equilateral
done
clear
View Answer play_arrow
question_answer 159) If the straight lines \[2x-3y+1=0\] and \[4x-6y+5=0\] are tangents to the same circle, then the radius of the circle is
A)
\[\frac{3}{2\sqrt{13}}\]
done
clear
B)
\[\frac{3}{4\sqrt{13}}\]
done
clear
C)
\[\frac{3}{8\sqrt{13}}\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 160) If \[A\,(5,-1)\] and \[B\,(-3,7)\] are two points on a circle and if \[P(x,y)\] is any point on the circle such that s\[\angle APB=\frac{\pi }{2},\] then the equation of the circle is
A)
\[{{x}^{2}}+{{y}^{2}}-2x+6y-22=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}+2x+6y-11=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}-2x+6y+22=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-2x-6y-22=0\]
done
clear
View Answer play_arrow
question_answer 161) The angle between the pair of straight lines represented by the equation \[12{{x}^{2}}+7xy-12{{y}^{2}}-x-7y-1=0\]is
A)
\[\frac{\pi }{3}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{\pi }{6}\]
done
clear
View Answer play_arrow
question_answer 162) The equation of a straight line which is parallel to \[x-2y+8=0\]and passes through \[(0,4)\] is
A)
\[x-2y+8=0~~~\]
done
clear
B)
\[x-2y+7=0\]
done
clear
C)
\[x-2y+4=0\]
done
clear
D)
\[2x+2y-13=0\]
done
clear
View Answer play_arrow
question_answer 163) The algebraic sum of the moments of the forces, forming a couple, about any point in their plane is
A)
proportional to the sum of the magnitudes of the forces
done
clear
B)
inversely proportional to the magnitudes of the forces
done
clear
C)
constant and is equal to the moment of the couple
done
clear
D)
constant and is equal to one-third of the moment of the couple
done
clear
View Answer play_arrow
question_answer 164) At time t, the distance x cm of a moving particle in a horizontal line is given by\[x=12\,{{t}^{3}}-7\,{{t}^{2}}+14t+2.\]. The acceleration when \[t=1\text{ }s\]is
A)
\[48\,\,cm/{{s}^{2}}\]
done
clear
B)
\[68\text{ }cm/{{s}^{2}}\]
done
clear
C)
\[58\text{ }cm/{{s}^{2}}\]
done
clear
D)
\[56\text{ }cm/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 165) The horizontal range of a projectile is \[\frac{4}{\sqrt{3}}\] times its maximum height. The angle of projection is
A)
\[{{30}^{o}}\]
done
clear
B)
\[{{60}^{o}}\]
done
clear
C)
\[{{45}^{o}}\]
done
clear
D)
\[{{\tan }^{-1}}\,(2)\]
done
clear
View Answer play_arrow
question_answer 166) A particle with uniform acceleration reaches \[100\text{ }m\]in the 5th second and \[151\text{ }m\]in the 8th second. The acceleration is
A)
\[15m/{{s}^{2}}\]
done
clear
B)
\[~16m/{{s}^{2}}\]
done
clear
C)
\[17\text{ }m/{{s}^{2}}\]
done
clear
D)
\[20\text{ }m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 167) Let \[\vec{u}\] and \[\vec{v}\] be the velocity vectors of a particle at a point O. If \[\vec{u}\] and \[\vec{v}\] are in opposite directions and if \[u>v,\] then the magnitude of the resultant velocity vector \[\vec{v}\] is
A)
\[u+v\]
done
clear
B)
\[2\,u+v\]
done
clear
C)
\[u-v\]
done
clear
D)
\[u-\frac{1}{2}v\]
done
clear
View Answer play_arrow
question_answer 168) The forces of magnitude \[9\text{ }N\]and \[11\text{ }N\]act at a point and are inclined to each other at an angle of\[{{45}^{o}}\]. The magnitude of the resultant force is
A)
\[\sqrt{301}\,N\]
done
clear
B)
\[\sqrt{202+99\sqrt{2}}\,N\]
done
clear
C)
\[\sqrt{{{9}^{2}}+{{11}^{2}}}\,\,N\]
done
clear
D)
\[202\,N\]
done
clear
View Answer play_arrow
question_answer 169) If X and Y are two non-singular matrices such that \[XY{{X}^{-1}}=\left( \begin{matrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -7 \\ \end{matrix} \right),\] then \[X{{Y}^{-1}}{{X}^{-1}}\] is equal to
A)
\[\left( \begin{matrix} \frac{1}{3} & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & -\frac{1}{7} \\ \end{matrix} \right)\]
done
clear
B)
\[\left( \begin{matrix} -\frac{1}{3} & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & -7 \\ \end{matrix} \right)\]
done
clear
C)
\[\left( \begin{matrix} \frac{1}{3} & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 7 \\ \end{matrix} \right)\]
done
clear
D)
\[\left( \begin{matrix} \frac{1}{3} & 0 & 0 \\ 0 & -\frac{1}{2} & 0 \\ 0 & 0 & 7 \\ \end{matrix} \right)\]
done
clear
View Answer play_arrow
question_answer 170) Let \[\vec{a}\,-\,2\vec{b}\] and \[2\vec{a}\,-\vec{b}\] be position vectors of the points A and B respectively. The position vector of the point which divides AB in the ratio \[3:2\]externally is
A)
\[\frac{8}{5}\,\vec{a}-\frac{7}{5}\vec{b}\]
done
clear
B)
\[4\,\vec{a}+\vec{b}\]
done
clear
C)
\[\,\vec{a}+4\vec{b}\]
done
clear
D)
\[\frac{7}{5}\vec{b}-\frac{8}{5}\vec{a}\]
done
clear
View Answer play_arrow
question_answer 171) If \[|\vec{a}|=2,\,|\vec{b}|=5,\] and \[\vec{a}\,.\,\vec{b}=5\sqrt{2},\]then \[|\vec{a}\times \vec{b}|\] is equal to
A)
\[5\sqrt{2}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
\[4\sqrt{2}\]
done
clear
D)
\[2\]
done
clear
View Answer play_arrow
question_answer 172) Let \[\vec{a}-2\vec{b}+3\vec{c},\,\,\,\,\,-2\vec{a}+3\vec{b}-\vec{c}\]and \[4\vec{a}-7\vec{b}+7\vec{c}\]be position vectors of the points A, B and C respectively. Then, the points A, B and Care
A)
vertices of an equilateral triangle
done
clear
B)
vertices of a right angled triangle
done
clear
C)
vertices of an isosceles triangle
done
clear
D)
collinear points
done
clear
View Answer play_arrow
question_answer 173) If \[\left| \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\ \end{matrix} \right|=3,\] then \[\left| \begin{matrix} 3\,{{a}_{1}} & 9\,{{b}_{1}} & 3\,{{c}_{1}} \\ {{a}_{2}} & 3\,{{b}_{2}} & {{c}_{2}} \\ 3\,{{a}_{3}} & 9\,{{b}_{3}} & 3\,{{c}_{3}} \\ \end{matrix} \right|\] is equal to
A)
\[51\]
done
clear
B)
\[27\]
done
clear
C)
\[81\]
done
clear
D)
\[91\]
done
clear
View Answer play_arrow
question_answer 174) The domain of the function \[f(x)=\frac{1}{{{\log }_{10}}\,(1-x)}\]is
A)
\[(-\infty ,\,1]\,-\{0\}\]
done
clear
B)
\[(-\infty ,\,1)\,-\{0\}\]
done
clear
C)
\[(-\infty ,\,\,2)\,\]
done
clear
D)
\[(0,\,-\infty )\,\]
done
clear
View Answer play_arrow
question_answer 175) If \[\omega \] is a complex cube root of unity, then \[\frac{a+b\omega +c{{\omega }^{2}}}{a{{\omega }^{2}}+b+c\omega }+\frac{a{{\omega }^{2}}+b\omega +c}{a+b{{\omega }^{2}}+c\omega }\] is equal to
A)
\[1\]
done
clear
B)
\[2\,\omega \]
done
clear
C)
\[2\,{{\omega }^{2}}\]
done
clear
D)
\[-1\]
done
clear
View Answer play_arrow
question_answer 176) If 19 times 12th term of an AP and 18 times 11 th term of an AP are equal, then the 30th term of the AP is
A)
\[0\]
done
clear
B)
\[2\]
done
clear
C)
\[11\]
done
clear
D)
\[29\]
done
clear
View Answer play_arrow
question_answer 177) Sum ton terms of the series \[1+11+111+....\]is
A)
\[\frac{10}{81}\,\,({{10}^{n}}-1)-\frac{n}{81}\]
done
clear
B)
\[\frac{10}{81}\,\,({{10}^{n}}-1)-\frac{n}{9}\]
done
clear
C)
\[\frac{10}{81}\,\,({{10}^{n}}-1)+\frac{n}{9}\]
done
clear
D)
\[\frac{10}{81}\,\,({{10}^{n}}-1)+\frac{n}{81}\]
done
clear
View Answer play_arrow
question_answer 178) If one root of the equation \[{{x}^{2}}-(3\sqrt{2}-2i)\,x-6\,\sqrt{2}i=0\] is \[-2i,\] then the other root of the equation is
A)
\[2i\]
done
clear
B)
\[3\,\sqrt{2}\]
done
clear
C)
\[-3\,\sqrt{2}\]
done
clear
D)
\[5\,\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 179) If \[{{z}_{1}}\] and \[{{z}_{2}}\] are non-zero complex numbers such that arg \[\left( \frac{{{z}_{1}}}{{{z}_{2}}} \right)=\frac{\pi }{2},\] then \[\left| \frac{3{{z}_{1}}-5{{z}_{2}}}{3{{z}_{1}}+5{{z}_{2}}} \right|\] equal to
A)
\[\sqrt{2}\]
done
clear
B)
\[\sqrt{34}\]
done
clear
C)
\[1\]
done
clear
D)
\[\frac{2}{\sqrt{34}}\]
done
clear
View Answer play_arrow
question_answer 180) Which one of the following is not true for the function \[f(x)={{x}^{2}}-x+1,\,0\le x\le 1\]?
A)
Increases on \[\left[ \frac{1}{2},1 \right]\]
done
clear
B)
Decreases on \[\left[ 0,\frac{1}{2} \right]\]
done
clear
C)
Increases on \[\left[ 0,\frac{1}{2} \right]\]
done
clear
D)
Neither increases nor decreases on \[[0,\,\,1]\]
done
clear
View Answer play_arrow
question_answer 181) The value of the integral \[\int{{{({{x}^{4}}+3{{x}^{3}}+9{{x}^{2}}+8x-6)}^{12}}}\] \[(4{{x}^{3}}+9{{x}^{2}}+18x+8)\,dx\] is equal to
A)
\[\frac{{{({{x}^{4}}+3{{x}^{3}}+9{{x}^{2}}+8x-6)}^{12}}}{12}+c\]
done
clear
B)
\[\frac{{{(4{{x}^{3}}+9{{x}^{2}}+18x+8)}^{13}}}{13}+c\]
done
clear
C)
\[\frac{{{({{x}^{4}}+3{{x}^{2}}+9{{x}^{2}}+8x-6)}^{13}}}{13}+c\]
done
clear
D)
\[\frac{{{({{x}^{4}}+3{{x}^{2}}+9{{x}^{2}}+8x-6)}^{11}}}{11}+c\]
done
clear
View Answer play_arrow
question_answer 182) \[\int{{{x}^{2}}\,{{7}^{x}}\,\,dx}\] is equal to
A)
\[\frac{{{x}^{2}}{{7}^{x}}}{\log \,7}+2x\frac{{{7}^{x}}}{{{(\log \,7)}^{2}}}+2\frac{{{7}^{x}}}{{{(\log \,7)}^{3}}}+c\]
done
clear
B)
\[\frac{{{x}^{2}}{{7}^{x}}}{\log \,7}-2x\frac{{{7}^{x}}}{{{(\log \,7)}^{2}}}+2\frac{{{7}^{x}}}{{{(\log \,7)}^{3}}}+c\]
done
clear
C)
\[{{x}^{2}}{{7}^{x}}-2x\,\frac{7x}{\log \,7}+2\,\frac{7x}{{{(\log \,7)}^{2}}}+c\]
done
clear
D)
\[\frac{{{x}^{2}}{{7}^{x}}}{{{(\log \,7)}^{2}}}-2x\,\frac{{{7}^{x}}}{{{(\log \,7)}^{3}}}+2\frac{{{7}^{x}}}{{{(\log \,7)}^{4}}}+c\]
done
clear
View Answer play_arrow
question_answer 183) If \[y=\cos \,(m\,\,{{\sin }^{-1}}\,x),\] then \[(1-{{x}^{2}})\,\frac{{{d}^{2}}y}{d{{x}^{2}}}-x\frac{dy}{dx}+{{m}^{2}}y\] is equal to
A)
\[1\]
done
clear
B)
\[7\]
done
clear
C)
\[-1\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 184) \[{{\cos }^{2}}\,B+{{\cos }^{2}}\,(A-B)\,-2\cos \,A\,\cos \,B\,\cos \,(A-B)\]is equal to
A)
\[co{{s}^{2}}\text{ }A\]
done
clear
B)
\[co{{s}^{2}}\text{ }A-1\]
done
clear
C)
\[si{{n}^{2}}\text{ }A\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 185) If \[A+B+C=\pi ,\]then \[\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}\]is equal to
A)
\[3\]
done
clear
B)
\[2\]
done
clear
C)
\[1\]
done
clear
D)
\[0\]
done
clear
View Answer play_arrow
question_answer 186) If \[{{\tan }^{-1}}\,(1-x),\,\,{{\tan }^{-1}}\,(x)\] and \[{{\tan }^{-1}}\,(1+x)\] are in AP, then the value of \[{{x}^{3}}+{{x}^{2}}\]is equal to
A)
\[2\]
done
clear
B)
\[-1\]
done
clear
C)
\[1\]
done
clear
D)
\[-2\]
done
clear
View Answer play_arrow
question_answer 187) \[{{\sin }^{-1}}x+{{\sec }^{-1}}x+{{\cot }^{-1}}x+{{\cos }^{-1}}x\]\[+\text{cose}{{\text{c}}^{-1}}\,x+{{\tan }^{-1}}x\] is equal to
A)
\[\pi \]
done
clear
B)
\[2\pi \]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\frac{3\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 188) The general solution of the equation\[sin\text{ }x+cos\text{ }x=2\]is
A)
\[x=n\pi \,+{{(-1)}^{n}}\,\frac{\pi }{4},\,n=....,-3,\,-2,\,\] \[-1,\,0,1,\,2,\,3,...\]
done
clear
B)
\[x=n\pi +{{(-1)}^{n}}\frac{\pi }{6},n=....,-3,-2,-1,\] \[0,\,1,\,2,\,3,....\]
done
clear
C)
\[x=n\pi +{{(-1)}^{n+1}}\frac{\pi }{4},n=...,-3,-2,\] \[-1,0,1,2,3,...\]
done
clear
D)
does not exist
done
clear
View Answer play_arrow
question_answer 189) If a \[\sin \theta +b\,\cos \theta =4\] and a \[\sin \theta -b\,\cos \theta =3,\]then the value of \[\sin 2\,\theta \] is
A)
\[\frac{7}{{{a}^{2}}+{{b}^{2}}}\]
done
clear
B)
\[\frac{5}{{{a}^{2}}+{{b}^{2}}}\]
done
clear
C)
\[\frac{7}{{{a}^{2}}-{{b}^{2}}}\]
done
clear
D)
\[\frac{7}{2ab}\]
done
clear
View Answer play_arrow
question_answer 190) \[(1-\tan A)\,(\cot \,A+1)\] is equal to
A)
\[(1-\tan A)\,(1+tanA)\]
done
clear
B)
\[(1+\tan A)\,(cot\,A-1)\]
done
clear
C)
\[(1+\tan A)\,(1-cot\,A)\]
done
clear
D)
\[(\tan \,A-1)\,(\cot \,A-1)\]
done
clear
View Answer play_arrow
question_answer 191) \[\int{{{\sec }^{2}}x\,\,\text{cose}{{\text{c}}^{2}}x\,\,dx}\]is equal to
A)
\[\tan x-\cot \,x+c\]
done
clear
B)
\[\tan x+\cot \,x+c\]
done
clear
C)
\[\tan x+\operatorname{cosec}\,x+c\]
done
clear
D)
\[\cot x+\operatorname{cosec}\,+c\]
done
clear
View Answer play_arrow
question_answer 192) The area of the region bounded by the curve \[x=2\,\cos \,\theta ,\,\,y=2\,\sin \theta ,\,x=0,\,x=2\] and the x-axis is (in sq unit)
A)
\[4\pi \]
done
clear
B)
\[2\pi \]
done
clear
C)
\[\pi \]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 193) The solution of the differential equation \[\frac{dy}{dx}=5+5x+10y+10xy\]is
A)
\[\log \,(5+10y)=x+\frac{{{x}^{2}}}{2}+c\]
done
clear
B)
\[\frac{1}{10}\log \,(5+10y)=x+\frac{{{x}^{2}}}{2}+c\]
done
clear
C)
\[\frac{1}{5}\log \,(5+10y)=x+\frac{{{x}^{2}}}{2}+c\]
done
clear
D)
\[\frac{1}{10}\log \,(5+10y)=x+{{x}^{2}}+c\]
done
clear
View Answer play_arrow
question_answer 194) The order and degree of the differential equation \[\frac{{{d}^{2}}y}{d{{x}^{2}}}+y+{{\left( \frac{dy}{dx}+\frac{{{d}^{3}}y}{d{{x}^{3}}} \right)}^{5/2}}=0\] are respectively
A)
\[3,\,\,\,2\]
done
clear
B)
\[2,\,\,3\]
done
clear
C)
\[3,\,\,1\]
done
clear
D)
\[3,\,\,5\]
done
clear
View Answer play_arrow
question_answer 195) \[\int_{0}^{\pi /2}{\frac{{{\sin }^{100}}x}{{{\sin }^{100}}x+{{\cos }^{100}}x}\,\,dx}\]is equal to
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[\frac{\pi }{12}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{8}\]
done
clear
View Answer play_arrow
question_answer 196) If \[(\vec{a}\times \vec{b})\times \vec{c}=\vec{a}\times (\vec{b}\times \vec{c})\]and \[\vec{a},\vec{b}\] and \[\vec{c}\] are not mutually perpendicular vectors, then
A)
\[\vec{a}\] and \[\vec{c}\] are parallel
done
clear
B)
\[\vec{a}\] and \[\vec{b}\] are parallel
done
clear
C)
\[\vec{b}\]and \[\vec{c}\] are parallel
done
clear
D)
\[\vec{a}\] and \[\vec{c}\]are perpendicular
done
clear
View Answer play_arrow
question_answer 197) Which me of the following is a point on the straight line \[\vec{r}=(-5\hat{i}+2\hat{j}+3\hat{k})\,+\,t\,(9\hat{i}-5\hat{j}+3\hat{k})\]?
A)
\[(13,-8,\,7)\]
done
clear
B)
\[(4,-3,\,5)\]
done
clear
C)
\[(-14,7,\,6)\]
done
clear
D)
\[(22,-13,12)\]
done
clear
View Answer play_arrow
question_answer 198) \[\vec{r}=(1-t)\,(3\hat{i}-4\hat{j}+7\hat{k})+t(\hat{i}+\hat{j}-\hat{k})\]\[+s(-2\hat{i}+\hat{j}-\hat{k})\] is the equation of a plane in vector form when it
A)
passes through three given non-collinear points
done
clear
B)
passes through one point and parallel to two vectors
done
clear
C)
passes through two points and parallel to one vector
done
clear
D)
passes through one point and perpendicular to one vector
done
clear
View Answer play_arrow
question_answer 199) The point of intersection of the lines \[\frac{x-1}{3}=\frac{y-1}{-1}=\frac{z+1}{0}\] and \[\frac{x-4}{2}=\frac{y}{0}=\frac{z+1}{3}\]is
A)
\[(4,0,1)\]
done
clear
B)
\[(4,0,-1)\]
done
clear
C)
\[(1,1,1)\]
done
clear
D)
\[(1,1,-1)\]
done
clear
View Answer play_arrow
question_answer 200) If \[3\hat{i}+\hat{j}-2\hat{k}\]and \[\hat{i}-3\hat{j}+4\hat{k}\] are the diagonals of a parallelogram, then the area of the parallelogram is
A)
\[10\sqrt{3}\] sq unit
done
clear
B)
\[5\sqrt{3}\] sq unit
done
clear
C)
\[5\sqrt{2}\]sq unit
done
clear
D)
\[10\sqrt{2}\]sq unit
done
clear
View Answer play_arrow
question_answer 201) \[\vec{a}=\hat{i}+2\hat{j}+3\hat{k},\,\,\,\,\,\vec{b}=-\hat{i}+2\hat{j}+3\hat{k}\] and \[\vec{c}=2\hat{i}-2\hat{j}-3\hat{k},\]then \[(\vec{b}+\vec{c}).\vec{a}\times \{(\vec{b}+\vec{c})\times \vec{a}\}\] is equal to
A)
\[9\]
done
clear
B)
\[21\]
done
clear
C)
\[13\]
done
clear
D)
\[7\]
done
clear
View Answer play_arrow
question_answer 202) The coefficient of \[{{x}^{4}}\]in the expansion of \[{{(1+x)}^{-2}},\]where \[|x|<1,\] is
A)
\[-5\]
done
clear
B)
\[5\]
done
clear
C)
\[4\]
done
clear
D)
\[-3\]
done
clear
View Answer play_arrow
question_answer 203) If \[m{{=}^{n}}{{C}_{2}},\] then \[^{m}{{C}_{2}}\] is equal to
A)
\[^{n+1}{{C}_{4}}\]
done
clear
B)
\[{{2}^{n+1}}{{C}_{4}}\]
done
clear
C)
\[{{3}^{n+1}}{{C}_{4}}\]
done
clear
D)
\[{{4}^{n+1}}{{C}_{4}}\]
done
clear
View Answer play_arrow
question_answer 204) \[\frac{1+\frac{1}{2!}+\frac{1}{4!}+\frac{1}{6!}+...}{\frac{1}{1!}+\frac{1}{3!}+\frac{1}{5!}+....}\] is equal to
A)
\[\frac{{{e}^{2}}-1}{{{e}^{2}}+1}\]
done
clear
B)
\[\frac{{{e}^{2}}+1}{{{e}^{2}}-1}\]
done
clear
C)
\[\frac{e+1}{e-1}\]
done
clear
D)
\[\frac{1-{{e}^{2}}}{e+{{e}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 205) Four arithmetic means between -10 and 25 are inserted. Then, the 5th term in the series is
A)
\[11\]
done
clear
B)
\[19\]
done
clear
C)
\[17\]
done
clear
D)
\[18\]
done
clear
View Answer play_arrow
question_answer 206) The mean deviation about the mean for the values 18, 20, 12, 14, 19, 22, 26, 16, 19, 24 is
A)
\[3.1\]
done
clear
B)
\[3.4\]
done
clear
C)
\[3.2\]
done
clear
D)
\[3.3\]
done
clear
View Answer play_arrow
question_answer 207) \[3\,{{\log }_{e}}2+\frac{1}{4}-\frac{1}{2}.\frac{1}{{{4}^{2}}}+\frac{1}{3}.\frac{1}{{{4}^{3}}}-....\]is equal to
A)
\[{{\log }_{e}}10\]
done
clear
B)
\[3\,\,{{\log }_{e}}4\]
done
clear
C)
\[2\,{{\log }_{e}}5\]
done
clear
D)
\[{{\log }_{e}}\,8\]
done
clear
View Answer play_arrow
question_answer 208) The number of ways of selecting a boy and a girl from a class consisting of 20 boys and 30 girls is
A)
\[50\]
done
clear
B)
\[10\]
done
clear
C)
\[600\]
done
clear
D)
\[1300\]
done
clear
View Answer play_arrow
question_answer 209) The sum of the coefficients in the expansion of \[{{(1+x-3x)}^{143}}\] is
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
\[-3\]
done
clear
D)
\[-7\]
done
clear
View Answer play_arrow
question_answer 210) If \[f(x)={{\cot }^{-1}}\left[ \sqrt{\frac{1+\sin x}{1-\sin x}} \right],\,0\le x\le \frac{\pi }{4},\]then \[f'\left( \frac{\pi }{4} \right)\] is equal to
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{-1}{2}\]
done
clear
C)
\[\frac{1-{{x}^{2}}}{1+{{x}^{2}}}\]
done
clear
D)
\[\frac{x}{1-{{x}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 211) For the function \[f(x)=|x-8|,\,0\le x\le 16,\] the Rollers theorem is not applicable as
A)
the function is not continuous at\[x=8\]
done
clear
B)
\[f(0)\ne f(16)\]
done
clear
C)
the function is not differentiable at \[x=8\]
done
clear
D)
the function is not differentiable at all points in \[(0,\,16)\]
done
clear
View Answer play_arrow
question_answer 212) If the tangent at \[x=c\] to the curve \[y={{x}^{3}}-5{{x}^{2}}-3x,\,1\le x\le 3,\]is parallel to the chord joining the points \[(1,-7)\] and \[(3,-27),\] then the value of c is equal to
A)
\[1\]
done
clear
B)
\[\frac{5}{3}\]
done
clear
C)
\[\frac{7}{3}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 213) If \[x=2\,\left[ \cos \theta +\log \,\left( \tan \frac{\theta }{2} \right) \right],y=2\,\,\sin \theta ,\]then \[\frac{dy}{dx}\]is
A)
\[\cot \theta \]
done
clear
B)
\[\cos \theta \]
done
clear
C)
\[\tan \theta \]
done
clear
D)
\[\sin \theta \]
done
clear
View Answer play_arrow
question_answer 214) If \[y=6\,\,\sin x\,{{\log }_{10}}x+{{e}^{{{x}^{2}}}},\] then \[\frac{dy}{dx}\] is equal to
A)
\[\frac{6\,\,\sin x}{x}+6\,\cos \,x\,{{\log }_{10}}\,x+2x{{e}^{{{x}^{2}}}}\]
done
clear
B)
\[\frac{6\,\,\sin x}{x}\,{{\log }_{10}}\,e+6\,\cos \,x\,{{\log }_{10}}x+2x{{e}^{{{x}^{2}}}}\]
done
clear
C)
\[6\,\cos \,x\,{{\log }_{10}}x+6\,\sin x.\frac{10}{x}+2x{{e}^{{{x}^{2}}}}\]
done
clear
D)
\[\frac{6\,\sin \,x}{x}+6\,\cos \,x\,{{\log }_{10}}x+x{{e}^{{{x}^{2}}}}\]
done
clear
View Answer play_arrow
question_answer 215) Two events A and 5 have probabilities \[0.3\] and \[0.4\] respectively. The probability that both A and B occur simultaneously is \[0.1\]. The probability that neither A nor B occur is
A)
\[0.2\]
done
clear
B)
\[0.3\]
done
clear
C)
\[0.4\]
done
clear
D)
\[0.1\]
done
clear
View Answer play_arrow
question_answer 216) \[\underset{n\to \infty }{\mathop{\lim }}\,\,\,\frac{{{2}^{n+1}}+{{3}^{n+1}}}{{{2}^{n}}+{{3}^{n}}}\]is equal to
A)
\[0\]
done
clear
B)
\[1\]
done
clear
C)
\[2\]
done
clear
D)
\[3\]
done
clear
View Answer play_arrow
question_answer 217) The value of n such that \[\underset{x\to 3}{\mathop{\lim }}\,\,\frac{{{x}^{n}}-{{3}^{n}}}{x-3}=108\]is
A)
\[3\]
done
clear
B)
\[7\]
done
clear
C)
\[6\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 218) If the function \[f(x)=\left\{ \begin{matrix} \frac{{{x}^{3}}-8}{{{x}^{2}}-4}, & if & x\ne 2 \\ k, & if & x=2 \\ \end{matrix} \right.\] is continuous at \[x=2,\]then the value of k is
A)
\[2\]
done
clear
B)
\[0\]
done
clear
C)
\[3\]
done
clear
D)
\[4\]
done
clear
View Answer play_arrow
question_answer 219)
The probability distribution of a random variable X is \[x=x\] \[-1\] \[0\] \[1\] \[2\] \[P(X=X)\] \[0.2\] \[0.1\] \[0.4\] \[\lambda \]
Then, \[P(0<X\le 2)\] is equal to
A)
\[0.8\]
done
clear
B)
\[0.6\]
done
clear
C)
\[0.5\]
done
clear
D)
\[0.7\]
done
clear
View Answer play_arrow
question_answer 220) The general solution of \[{{\cot }^{2}}\theta =3\] is
A)
\[2n\pi \pm \frac{\pi }{3},n\in Z\]
done
clear
B)
\[n\pi \pm \frac{\pi }{6},n\in Z\]
done
clear
C)
\[n\pi \pm \frac{\pi }{2},n\in Z\]
done
clear
D)
\[2n\pi \pm \frac{\pi }{6},n\in Z\]
done
clear
View Answer play_arrow
question_answer 221) If A and B are square matrices such that \[AB\text{ }=A\]and \[BA=B,\]then \[{{A}^{2}}+{{B}^{2}}\]is equal to
A)
\[AB\]
done
clear
B)
\[A+B\]
done
clear
C)
\[BA+B\]
done
clear
D)
\[AB+A\]
done
clear
View Answer play_arrow
question_answer 222) If A is a square matrix of order 3 and if \[\det \,(A)=3,\] then \[\det \,[adj\,\,\{adj\,(adj\,A)\}]\] is equal to
A)
\[{{81}^{2}}\]
done
clear
B)
\[81\]
done
clear
C)
\[729\]
done
clear
D)
\[27\]
done
clear
View Answer play_arrow
question_answer 223) The value of the determinant \[\left| \begin{matrix} 1+\log \,a & \log \,b & \log \,c \\ \log \,a & 1+\log \,b & \log \,c \\ \log \,a & \log \,b & 1+\log \,c \\ \end{matrix} \right|\]is equal to
A)
\[\log \,(abc)\]
done
clear
B)
\[1-\log \,\,abc\]
done
clear
C)
\[\log \,(a+b+c)\]
done
clear
D)
\[1+\,\log \,abc\]
done
clear
View Answer play_arrow
question_answer 224) If A and Bare square matrices of order 3 such that \[det\text{ }A=1\] and \[det\text{ }B=-1~\]then \[det\text{ (-10}\,\text{AB)}\] is equal to
A)
\[10\]
done
clear
B)
\[-10\]
done
clear
C)
\[-1000\]
done
clear
D)
\[1000\]
done
clear
View Answer play_arrow
question_answer 225) \[{{\sin }^{2}}\,\frac{\pi }{8}+{{\sin }^{2}}\,\frac{3\pi }{8}+{{\sin }^{2}}\frac{5\pi }{8}+{{\sin }^{2}}\frac{7\pi }{8}\]is equal to
A)
\[1\]
done
clear
B)
\[\frac{3}{2}\]
done
clear
C)
2
done
clear
D)
\[\frac{5}{2}\]
done
clear
View Answer play_arrow
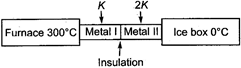 The coefficient of thermal conductivities of the metals are K and \[2K\]respectively. If the furnace temperature at one end is \[{{300}^{o}}C\]and ice box temperature at the other end is \[{{0}^{o}}C,\] then the junction temperature is
The coefficient of thermal conductivities of the metals are K and \[2K\]respectively. If the furnace temperature at one end is \[{{300}^{o}}C\]and ice box temperature at the other end is \[{{0}^{o}}C,\] then the junction temperature is