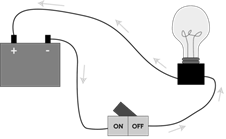
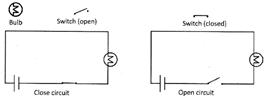
 The electric circuit can be diagrammatically represented with the help of a circuit diagram. A circuit diagram represents circuit using symbols for its components.
The electric circuit can be diagrammatically represented with the help of a circuit diagram. A circuit diagram represents circuit using symbols for its components.
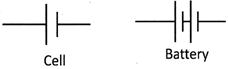
 Resistance
The electrical resistance of a material is the measure of hindrance, the material creates in the flow of electric current through it. The high the resistance of a material, less the amount of current flows through it.
In addition to material, the resistance also depends on the thickness and length of the material used. A thin wire has a higher resistance than a thick wire. Similarly a long wire has a higher resistance than a short wire.
Material such as metals have low electrical resistance. These materials allow electricity to flow through them and are called good conductors or simply conductors.
Material such as wood, rubber and plastic have high electrical resistance. These materials do not conduct electricity. These are called bad conductors or insulators.
Heating Effect of Current
Heat is produced when current flows through a conductor. The heat produced depends upon the following factors:
Resistance
The electrical resistance of a material is the measure of hindrance, the material creates in the flow of electric current through it. The high the resistance of a material, less the amount of current flows through it.
In addition to material, the resistance also depends on the thickness and length of the material used. A thin wire has a higher resistance than a thick wire. Similarly a long wire has a higher resistance than a short wire.
Material such as metals have low electrical resistance. These materials allow electricity to flow through them and are called good conductors or simply conductors.
Material such as wood, rubber and plastic have high electrical resistance. These materials do not conduct electricity. These are called bad conductors or insulators.
Heating Effect of Current
Heat is produced when current flows through a conductor. The heat produced depends upon the following factors:
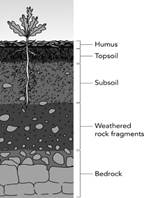 A-horizon: This is the uppermost layer of the soil. This layer is also called topsoil. It is dark in colour due to the presence of humus.
B-horizon: This layer is below the topsoil and is called subsoil. This soil is lighter in colour. The particles of this layer are coarser and porous. This layer does not contain much humans and thus not suitable for plants growth.
C-horizon: This layer is below subsoil and is called substratum. This layer is derived from hard rocks that lie beneath it.
R-horizon: This layer is below the substratum. It consists of hard rock called bedrock. Water cannot penetrate the bedrock and thus accumulates in the substratum.
Components of Soil
Main components of soil are different sized rock particles and humus. On the basis of their sizes, rock particles have been classified into four groups.
Clay: Clays are the smallest rock particles present in the soil. They are smooth to touch.
Silt: Silts are the rock particles which are a little larger than clay particles. Silt particles are not as smooth as clay particles.
Sand: Rock particles which are larger than silt particles form sand. Sand particles have rough texture.
Gravel: The largest rock particles present in the soil form gravel.
Types of Soil
Sandy Soil: It consists of mainly sand. A little amount of silt and clay are also present in it.
Clayey Soil: It consists of mainly clay particles. Clay particles are very fine so it has very good water holding capacity.
Loamy Soil: Loamy soil consists of clay, silt and sand in right proportion. It also contains sufficient amount of humus. Therefore, loamy soil is the most fertile soil.
Forests: Our Lifeline
Forests are important for maintaining environmental balance and controlling pollution.
Functions of Forests
A-horizon: This is the uppermost layer of the soil. This layer is also called topsoil. It is dark in colour due to the presence of humus.
B-horizon: This layer is below the topsoil and is called subsoil. This soil is lighter in colour. The particles of this layer are coarser and porous. This layer does not contain much humans and thus not suitable for plants growth.
C-horizon: This layer is below subsoil and is called substratum. This layer is derived from hard rocks that lie beneath it.
R-horizon: This layer is below the substratum. It consists of hard rock called bedrock. Water cannot penetrate the bedrock and thus accumulates in the substratum.
Components of Soil
Main components of soil are different sized rock particles and humus. On the basis of their sizes, rock particles have been classified into four groups.
Clay: Clays are the smallest rock particles present in the soil. They are smooth to touch.
Silt: Silts are the rock particles which are a little larger than clay particles. Silt particles are not as smooth as clay particles.
Sand: Rock particles which are larger than silt particles form sand. Sand particles have rough texture.
Gravel: The largest rock particles present in the soil form gravel.
Types of Soil
Sandy Soil: It consists of mainly sand. A little amount of silt and clay are also present in it.
Clayey Soil: It consists of mainly clay particles. Clay particles are very fine so it has very good water holding capacity.
Loamy Soil: Loamy soil consists of clay, silt and sand in right proportion. It also contains sufficient amount of humus. Therefore, loamy soil is the most fertile soil.
Forests: Our Lifeline
Forests are important for maintaining environmental balance and controlling pollution.
Functions of Forests
| Scores | Tally Mark | Frequency |
| 0 | II | 2 |
| 1 | I | 1 |
| 25 | I | 1 |
| more...
Geometry
In our daily life we observe different geometrical shapes. These geometrical shapes are not only the matter of study of mathematics but are directly related with our daily life. The basic geometrical figures are made up of lines and angles.
Line Segment
It is the straight path between two points. In other words we can say that it has two end points and is of finite length.
Ray
When a line segment extends infinitely in one direction, it is called a ray. Simply we can say that a ray has one end point and infinite length.
Line
When both end of a line segment extended infinitely, it is known as a line. Simply we can say that a line has no end point and infinite length.
Parallel Lines
Two lines are said to be parallel if the distance between them always remains same at each and every point. The parallel lines never intersect each other.
In other words we can say that if two lines do not have any common point than they are said to be parallel. In the figure I and m are parallel lines.
Mensuration
Standard Units of Area
The inter relationship among various units of measurement of area are listed below.
\[1\,{{m}^{2}}\] = \[(100\times 100)\,c{{m}^{2}}={{10}^{4}}\,c{{m}^{2}}\]
\[1\,{{m}^{2}}\] = \[(10\times 10)\,d{{m}^{2}}=100\,d{{m}^{2}}\]
\[1\,d{{m}^{2}}\] = \[(10\times 10)\,c{{m}^{2}}=100\,c{{m}^{2}}\]
\[1\,da{{m}^{2}}\] = \[(10\times 10)\,{{m}^{2}}=100\,{{m}^{2}}\]
\[1\,h{{m}^{2}}\] = \[(100\times 100)\,{{m}^{2}}={{10}^{4}}{{m}^{2}}\]
\[1\,k{{m}^{2}}\] = \[(1000\times 1000)\,{{m}^{2}}={{10}^{6}}\,{{m}^{2}}\]
\[1\,hectare\] = \[10000\,{{m}^{2}}\]
\[1\,k{{m}^{2}}\] = \[100\,hectare\]
Formula Related to Perimetre and Area
Algebraic Expressions
In an algebraic expression constant and variables are linked with arithmetic operations.
The value of unknown variable is obtained by simplification of the given expression.
Terms of an algebraic Expression
Variables
Alphabetical symbols used in algebraic expressions are called variables a, b, c, d, m, n, x, y, z ........... etc. are some common letters which are used for variables.
Constant Terms
The symbol which itself indicate a permanent value is called constant. All numbers are constant.
\[6,10,\frac{10}{11},15,-6,\sqrt{3}....\]etc. are constants because, their values are fixed.
Variable Terms
A term which contains various numerical values is called variable term. For example. Product of \[\text{X=4 }\!\!\times\!\!\text{ }\,\text{X=4X}\]Product of \[\text{2,X,}{{\text{Y}}^{2\,}}\] and \[\text{Z=}\,\text{2 }\!\!\times\!\!\text{ X }\!\!\times\!\!\text{ }{{\text{Y}}^{\text{2}}}\text{ }\!\!\times\!\!\text{ Z=2X}{{\text{Y}}^{\text{2}}}\text{Z}\]
Thus, 4X and \[\text{2X}{{\text{Y}}^{\text{2}}}\text{Z}\] are variable terms
Types of Terms
There are two types of terms, like and unlike. Terms are classified by similarity of their variables.
Like and unlike Terms
The terms having same variables are called like terms and the terms having different variables are called unlike terms. For example, \[6x,\,x,\,-2x,\,\frac{4}{9}x,\]are like terms and \[6x,\,2{{y}^{2}},\,-9{{x}^{2}}yz,4xy,\]are unlike terms.
Coefficient
A number or a symbol multiplied with a variable in an algebraic expression is called its coefficient. In\[-6{{m}^{2}}np\], coefficient of\[n{{m}^{2}}p\] is \[-6\] because \[{{\text{m}}^{\text{2}}}np\]is multiplied with \[-6\] to from \[-6{{m}^{2}}np\].
The variable part of the term is called its variable or literal coefficient. In\[-\frac{5}{4}abc\], variable coefficients are a, b and c.
The constant part of the term is called constant coefficient.
In term\[-\frac{5}{4}abc\], constant coefficient is\[-\frac{5}{4}\].
Example: Sign of resulting addition of two like terms depends on which one of the following?
(a) Sign of biggest term
(b) Sign of smallest term
(c) Sign of positive term
(d) Sign of negative term
(e) None of these
Answer (a)
Operations on Algebraic Expressions
When constant and variables are linked with any of the following fundamental arithmetic operations i.e. addition, subtraction, multiplication and division, then the solution of the expression is obtained by simplification of the expression.
Addition and Subtraction of Terms
The addition of two unlike terms is not possible and their addition is obtained in the same form. Addition of \[2x+3x\] is \[5x\] but the addition of \[2x+3y\] is\[2x+3y\].
Subtraction of two like terms is same as the subtraction of whole numbers. For example,\[4x-2x=2x\]
Example: Simplify: \[(2{{x}^{2}}+{{x}^{2}})-(5{{x}^{2}}+11{{x}^{2}})\]
(a) \[15{{x}^{3}}\] (b) \[15{{x}^{2}}\]
(c) \[-3{{x}^{2}}\] (d) \[13{{x}^{2}}\]
(e) None of these
Answer (c)
Explanation:\[(2{{x}^{2}}+{{x}^{2}})-(5{{x}^{2}}+11{{x}^{2}})\] = \[3{{x}^{2}}-16{{x}^{2}}=-13{{x}^{2}}\]
Example: Evaluate:
\[[\{({{x}^{2}}+3{{x}^{2}})-({{x}^{2}}+{{x}^{2}})5\}\div x]\]
(a) \[-10x\] (b) \[-15x\]
(c) \[-6x\] (d) \[10x\]
(e) None of these
Answer (c)
Explanation:\[(4{{x}^{2}}-5\times 2{{x}^{2}})\div x=\]\[\frac{4{{x}^{2}}-10{{x}^{2}}}{x}\] \[=\frac{-6{{x}^{2}}}{x}=-6x\]
Equation
An equation is a condition on a variable. For example, the expression \[10x+3=13\] is an equation which describe that the variable is equal to a fixed number.
This value itself is called the solution of the equation.
Thus,\[10x+3=\]\[13\Rightarrow 10x\]\[=13-3=\]\[10\Rightarrow x=1\]
Here the definite value of the variable x in the equation \[10x+3=13\]
Note:
(i) An equation has two sides, LHS and RHS, between them more...
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |