Current Affairs JEE Main & Advanced

When the variable in a definite integral is changed, the substitutions in terms of new variable should be effected at three places.     (i) In the integrand (ii)In the differential i.e., \[dx\] (iii) In the limits     For example, if we put \[\varphi (x)=t\] in the integral \[\int_{a}^{b}{f\{\varphi (x)\}\varphi '(x)dx}\], then \[\int_{a}^{b}{f\{\varphi (x)\}\varphi '(x)dx=\int_{\varphi (a)}^{\varphi (b)}{f(t)\,dt}}\].

(1) \[\int_{a}^{b}{f(x)dx}=\int_{a}^{b}{f(t)\,dt}\] i.e., The value of a definite integral remains unchanged if its variable is replaced by any other symbol.     (2) \[\int_{a}^{b}{f(x)dx=-\int_{b}^{a}{f(x)dx}}\] i.e., by the interchange in the limits of definite integral, the sign of the integral is changed.     (3) \[\int_{a}^{b}{f(x)dx=\int_{a}^{c}{f(x)dx}+\int_{c}^{b}{f(x)dx}}\],   (where \[a<c<b\])      or \[\int_{a}^{b}{f(x)dx}=\int_{a}^{{{c}_{1}}}{f(x)dx}+\int_{{{c}_{1}}}^{{{c}_{2}}}{f(x)dx+.....+\int_{{{c}_{n}}}^{b}{f(x)dx;}}\] (where \[a<{{c}_{1}}<{{c}_{2}}<........{{c}_{n}}<b\])     Generally this property is used when the integrand has two or more rules in the integration interval.     This is useful when \[f\,(x)\] is not continuous in \[[a,\,\,b]\] because we can break up the integral into several integrals at the points of discontinuity so that the function is continuous in the sub-intervals.     (4) \[\int_{0}^{a}{f(x)dx=\int_{0}^{a}{f(a-x)dx}}\] : This property can be used only when lower limit is zero. It is generally used for those complicated integrals whose denominators are unchanged when \[x\] is replaced by \[(a-x)\].     Following integrals can be obtained with the help of above property.     (i) \[\int_{0}^{\pi /2}{\frac{{{\sin }^{n}}x}{{{\sin }^{n}}x+{{\cos }^{n}}x}}\,dx=\int_{0}^{\pi /2}{\frac{{{\cos }^{n}}x}{{{\cos }^{n}}x+{{\sin }^{n}}x}dx=\frac{\pi }{4}}\]         (ii) \[\int_{0}^{\pi /2}{\frac{{{\tan }^{n}}x}{1+{{\tan }^{n}}x}dx=\int_{0}^{\pi /2}{\frac{{{\cot }^{n}}x}{1+{{\cot }^{n}}x}dx=\frac{\pi }{4}}}\]     (iii) \[\int_{0}^{\pi /2}{\frac{1}{1+{{\tan }^{n}}x}dx=\int_{0}^{\pi /2}{\frac{1}{1+{{\cot }^{n}}x}}dx=\frac{\pi }{4}}\]         (iv) \[\int_{0}^{\pi /2}{\frac{{{\sec }^{n\,}}x}{{{\sec }^{n}}\,x+\text{cose}{{\text{c}}^{n}}x}\,dx=}\int_{0}^{\pi /2}{\,\,\,\,}\frac{\text{cose}{{\text{c}}^{n\,}}x}{\text{cose}{{\text{c}}^{n}}\,x+{{\sec }^{n}}x}\,dx=\frac{\pi }{4}\]     (v) \[\int_{0}^{\pi /2}{\,\,\,f(\sin 2x)\sin xdx=}\int_{0}^{\pi /2}{\,\,\,f(\sin 2x)\cos xdx}\]     (vi) \[\int_{0}^{\pi /2}{f(\sin x)dx=\int_{0}^{\pi /2}{\,\,\,\,f(\cos x)dx}}\]              (vii) \[\int_{0}^{\pi /4}{\log (1+\tan x)dx=\frac{\pi }{8}\log 2}\]             (viii) \[\int_{0}^{\pi /2}{\,\,\,\,\,\log \sin xdx}=\int_{0}^{\pi /2}{\,\,\,\,\,\log \cos xdx}=\frac{-\pi }{2}\log 2=\frac{\pi }{2}\log \frac{1}{2}\]     (ix) \[\int_{0}^{\pi /2}{{}}\frac{a\,\sin \,x+b\,\cos \,x}{\sin \,x+\cos \,x}\,dx=\int_{0}^{\pi /2}{{}}\frac{a\,\sec \,x+b\,\text{cosec}\,x}{\sec \,x+\text{cosec}\,x}\,dx\]\[\int_{0}^{\pi /2}{{}}\frac{a\,\sin \,x+b\,\cos \,x}{\sin \,x+\cos \,x}\,dx=\int_{0}^{\pi /2}{{}}\frac{a\,\sec \,x+b\,\cos ec\,x}{\sec \,x+\cos ec\,x}\,dx=\int_{0}^{\pi /2}{{}}\frac{a\,\tan \,x+b\,\cot \,x}{\tan \,x+\cot \,x}\,dx=\frac{\pi }{4}(a+b)\]     (5) \[\int_{-a}^{a}{{}}f(x)\,dx=\int_{0}^{a}{\text{ }\!\![\!\!\text{ }f(x)\,+f(-x)\text{ }\!\!]\!\!\text{ }}\text{ }dx\].     In special case :     \[\int_{-a}^{a}{f(x)\,dx}=\left\{ \begin{array}{*{35}{l}} 2\int_{0}^{a}{f(x)\,dx},\,\,\text{if}\,f(x)\,\,\text{is}\,\,\text{even function or }f(-x)=f(x)\text{ }  \\ \,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\text{if}\,\,f(x)\,\,\text{is odd function or }f(-x)=-f(x)  \\\end{array} \right.\]       This property is generally used when integrand is either even or odd function of \[x\].     (6) \[\int_{0}^{2a}{\,\,f(x)dx}=\int_{0}^{a}{f(x)dx+\int_{0}^{a}{{}}\text{ }f(2a-x)\,dx}\]     In particular, \[\int_{0}^{2a}{{}}\,f(x)\,dx\,=\,\left\{ \begin{array}{*{35}{l}} 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\text{if}\,\,\,\,f(2a- x)=-f(x)  \\ 2\int_{0}^{a}{f(x)\,dx}\,,\,\,\,\text{if}\,\,\,\,\,f(2a-x)=f(x)  \\ \end{array} \right.\]     It is generally used to make half the upper limit.     (7) \[\int_{a}^{b}{f(x)\,}dx=\int_{a}^{b}{f(a+b-x)dx}\].     (8) \[\int_{0}^{a}{\,\,x\,f(x)dx}=\frac{1}{2}a\int_{0}^{a}{\,\,f(x)dx}\], if \[f(a-x)=f(x)\].     (9) If \[f(x)\] is a periodic function with period T, then \[\int_{0}^{nT}{f(x)dx=n\int_{0}^{T}{\,\,f(x)dx}}\]     Deduction : If \[f(x)\] is a periodic function with period T, then     \[\int_{a}^{a+nT}{{}}f(x)\,dx=n\,\int_{0}^{T}{{}}f(x)\,dx\] , where \[n\,\in \,I\]     (a) If \[a=0,\] \[\int_{0}^{nT}{{}}f(x)\,dx=n\int_{0}^{T}{{}}f(x)\,dx,\] where \[n\in I\]     (b) If \[n=1,\] \[\int_{0}^{a+T}{{}}f(x)\,dx=\int_{0}^{T}{{}}f(x)\,dx\].     (10) \[\int_{mT}^{nT}{{}}f(x)\,dx=(n-m)\,\,\int_{0}^{T}{{}}f(x)\,dx,\] where \[n,\] \[m\in I\].     (11) \[\int_{a+nT}^{b+nT}{{}}f(x)\,dx=\int_{a}^{b}{{}}f(x)\,dx,\] where \[n\in \,I\].     (12) \[\int_{0}^{2k}{(x-[x])\,dx=k,}\] where \[k\] an integer, since \[x-[x]\] is a periodic function with period 1.     (13) If \[f(x)\] is a periodic function with period T, then \[\int_{a}^{a+T}{{}}f(x)\] is independent of a.     (14) \[\int_{a}^{b}{{}}f(x)\,dx=(b-a)\,\int_{0}^{1}{{}}f((b-a)\,x+a)\,dx\].

We know that \[\int_{a}^{b}{f(x)dx}=\underset{n\to \infty }{\mathop{\lim }}\,h\sum\limits_{r=1}^{n}{f(a+rh)}\], where \[nh=b-a\]     Now, put  \[a=0,\] \[b=1,\] \[\therefore \] \[nh=1\] or \[h=\frac{1}{n}\].     Hence \[\int_{0}^{1}{f(x)\,dx=\underset{n\to \infty }{\mathop{\lim }}\,}\frac{1}{n}\sum\limits_{{}}^{{}}{f\left( \frac{r}{n} \right)}\].     Express the given series in the form \[\sum{\frac{1}{n}f\left( \frac{r}{h} \right)}\].     Replace \[\frac{r}{n}\]by \[x,\,\,\frac{1}{n}\] by \[dx\] and the limit of the sum is \[\int_{0}^{1}{{}}f(x)\,dx\].

\[\int_{0}^{\infty }{{{x}^{n-1}}}{{e}^{-x}}dx\], \[n>0\] is called Gamma function and denoted by \[\Gamma n\]. If \[m\] and \[n\] are non-negative integers, then     \[\int_{0}^{\pi /2}{{{\sin }^{m}}x{{\cos }^{n}}xdx}=\frac{\Gamma \left( \frac{m+1}{2} \right)\,\Gamma \left( \frac{n+1}{2} \right)}{2\Gamma \left( \frac{m+n+2}{2} \right)}\]     where \[\Gamma (n)\] is called gamma function which satisfy the following properties \[\Gamma (n+1)=n\Gamma (n)=n!\]i.e.,\[\Gamma \,(1)=1\], \[\Gamma (1/2)=\sqrt{\pi }\]     In place of gamma function, we can also use the following formula \[\int_{0}^{\pi /2}{{{\sin }^{m}}x{{\cos }^{n}}xdx}\]     =\[\frac{(m-1)(m-3).....(2\text{ or }1)(n-1)(n-3).....(2\text{ or 1)}}{(m+n)(m+n-2)....(2\text{ or }1)}\]     It is important to note that we multiply by \[(\pi /2);\] when both \[m\] and \[n\] are even.

(1) \[\int_{0}^{\infty }{{{e}^{-ax}}\sin bxdx}=\frac{b}{{{a}^{2}}+{{b}^{2}}}\]           (2)  \[\int_{0}^{\infty }{{{e}^{-ax}}\cos bxdx}=\frac{a}{{{a}^{2}}+{{b}^{2}}}\]          (3)  \[\int_{0}^{\infty }{{{e}^{-ax}}}{{x}^{n}}dx=\frac{n!}{{{a}^{n}}+1}\]

\[\int_{0}^{\pi /2}{{{\sin }^{n}}xdx}=\int_{0}^{\pi /2}{{{\cos }^{n}}xdx}\]     \[\int_{0}^{\pi /2}{{{\sin }^{n}}xdx}=\int_{0}^{\pi /2}{{{\cos }^{n}}xdx}=\left\{ \begin{matrix} \frac{n-1}{n}.\frac{n-3}{n-2}.\frac{n-5}{n-4}......\frac{2}{3},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{when }n\text{ is odd}  \\ \frac{n-1}{n}.\frac{n-3}{n-2}.\frac{n-5}{n-4}.......\frac{3}{4}.\frac{1}{2}.\frac{\pi }{2},\,\,\,\,\,\text{when }n\text{ is even}  \\ \end{matrix} \right.\]     \[\int_{0}^{\pi /2}{{{\sin }^{m}}x{{\cos }^{n}}dx}=\frac{(m-1)\,(m-3).....(n-1)\,(n-3)....}{(m+n)\,(m+n-2)\,...(2\text{ or }1)}\],  [If \[m,\,\,n\] are both odd positive integers or one odd positive integer]     \[\int_{\,0}^{\,\pi /2}{{{\sin }^{m}}x{{\cos }^{n}}xdx}=\frac{(m-1)\,(m-3)............(n-1)\,(n-3)}{(m+n)\,(m+n-2)........(2\text{ or }1)}.\frac{\pi }{2}\], [If \[m,\,\,n\] are both positive integers]

(1) If  \[f(x)\] is continuous and \[u(x),\,\,v(x)\] are differentiable functions in the interval \[[a,\,\,b]\] then,     \[\frac{d}{dx}\int_{u(x)}^{v(x)}{f(t)dt=f\{v(x)\}\frac{d}{dx}}\{v(x)\}-f\{u(x)\}\frac{d}{dx}\{u(x)\}\].     (2) If the function \[\varphi \,(x)\] and \[\psi \,(x)\] are defined on \[[a,\,\,b]\] and differentiable at a point \[x\in \,(a,b),\] and \[f(x,t)\] is continuous, then, \[\frac{d}{dx}\,\left[ \int_{\varphi (x)}^{\psi (x)}{{}}f(x,t)\,dt \right]\]\[=\int_{\varphi (x)}^{\psi (x)}{\frac{d}{dx}}\,f(x,t)\,dt+\left\{ \frac{d\,\psi (x)}{dx} \right\}\,f(x,\psi (x))\]\[-\left\{ \frac{d\varphi (x)}{dx} \right\}f(x,\,\varphi (x))\].

(1) When both curves intersect at two points and their common area lies between these points: If the curves \[{{y}_{1}}={{f}_{1}}(x)\] and \[{{y}_{2}}={{f}_{2}}(x),\] where\[\,{{f}_{1}}(x)\,>\,{{f}_{2}}(x)\] intersect in two points \[A(x=a)\] and \[B(x=b)\], then common area between the curves is  \[=\int\limits_{a}^{b}{({{y}_{1}}-{{y}_{2}})\,dx}\]\[=\int\limits_{a}^{b}{[{{f}_{1}}(x)-{{f}_{2}}(x)]\,dx}\].     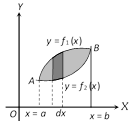(2) When two curves intersect at a point and the area between them is bounded by x-axis: Area bounded by the curves \[{{y}_{{}}}={{f}_{1}}(x),{{y}_{2}}={{f}_{2}}(x)\,\,\text{and}\,x-\text{axis}\]is  \[\int\limits_{a}^{\alpha }{{{f}_{1}}(x)dx+\int\limits_{\alpha }^{b}{{{f}_{2}}(x)dx}}\], 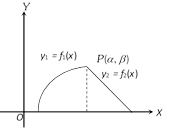    where \[P(\alpha ,\beta )\,\]is the point of intersection of the two curves.     (3) Positive and negative area : Area is always taken as positive. If some part of the area lies above the x-axis and some part lies below x-axis, then the area of two parts should be calculated separately and then add their numerical values to get the desired area.

(1) If \[{{I}_{n}}=\int_{0}^{\pi /4}{{{\tan }^{n}}xdx}\] then \[{{I}_{n}}+{{I}_{n-2}}=\frac{1}{n-1}\]     (2) If \[{{I}_{n}}=\int_{0}^{\pi /4}{{{\cot }^{n}}xdx}\] then \[{{I}_{n}}+{{I}_{n-2}}=\frac{1}{1-n}\]     (3) If \[{{I}_{n}}=\int_{0}^{\pi /4}{{{\sec }^{n}}x\,dx}\] then \[{{I}_{n}}=\frac{{{(\sqrt{2})}^{n-2}}}{n-1}+\frac{n-2}{n-1}{{I}_{n-2}}\]     (4) If \[{{I}_{n}}=\int_{0}^{\pi /4}{\text{cose}{{\text{c}}^{\text{n}}}x\,dx}\] then \[{{I}_{n}}=\frac{{{(\sqrt{2})}^{n-2}}}{n-1}+\frac{n-2}{n-1}{{I}_{n-2}}\]     (5) If \[{{I}_{n}}=\int_{0}^{\pi /2}{{{\sin }^{n}}x\,}dx,\,\] then \[{{I}_{n}}=\frac{n-1}{n}{{I}_{n-2}}\]     (6) If \[{{I}_{n}}=\int_{0}^{\pi /2}{{{\cos }^{n}}x\,dx,}\] then \[{{I}_{n}}=\frac{n-1}{n}{{I}_{n-2}}\].     (7) If \[{{I}_{n}}=\int_{0}^{\pi /2}{{{x}^{n}}\sin x\,dx}\] then \[{{I}_{n}}+n(n-1){{I}_{n-2}}=n{{(\pi /2)}^{n-1}}\]     (8) If \[{{I}_{n}}=\int_{0}^{\pi /2}{{{x}^{n}}\cos x\,dx}\] then \[{{I}_{n}}+n(n-1){{I}_{n-2}}=\,{{(\pi /2)}^{n}}\]     (9)  If \[a>b>0,\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x}}=\frac{2}{\sqrt{{{a}^{2}}-{{b}^{2}}}}{{\tan }^{-1}}\sqrt{\frac{a+b}{a-b}}\]     (10)If \[n\,\in \,I\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x}}=\frac{1}{\sqrt{{{b}^{2}}-{{a}^{2}}}}\log \left| \frac{\sqrt{b+a}-\sqrt{b-a}}{\sqrt{b+a}+\sqrt{b-a}} \right|\]     (11) If \[a>b>0\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\sin x}=\frac{2}{\sqrt{{{a}^{2}}-{{b}^{2}}}}{{\tan }^{-1}}\sqrt{\frac{a-b}{a+b}}}\]     (12) If \[0<a<b\], then     \[\int_{0}^{\pi /2}{\frac{dx}{a+b\sin x}}=\frac{1}{\sqrt{{{b}^{2}}-{{a}^{2}}}}\log \left| \frac{\sqrt{b+a}+\sqrt{b-a}}{\sqrt{b+a}-\sqrt{b-a}} \right|\]     (13) If \[a>b,\,{{a}^{2}}>{{b}^{2}}+{{c}^{2}},\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x+c\sin x}}\]\[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x+c\sin x}}=\frac{2}{\sqrt{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}}\,{{\tan }^{-1}}\frac{a-b+c}{\sqrt{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}}\]     (14) If \[a>b,\,{{a}^{2}}<{{b}^{2}}+{{c}^{2}},\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x+c\sin x}}\] \[=\frac{1}{\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}\] \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x+c\sin x}=\frac{1}{\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}}\log \left| \frac{a-b+c-\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}{a-b+c+\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}} \right|\]     (15) If \[a<b,\] \[{{a}^{2}}<{{b}^{2}}+{{c}^{2}}\] then \[\int_{0}^{\pi /2}{\frac{dx}{a+b\cos x+c\sin x}}\]\[=\frac{-1}{\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}\log \left| \frac{b-a-c-\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}{b-a-c+\sqrt{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}} \right|\].

If a plane curve is revolved about some axis in the plane of the curve, then the body so generated is known as solid of revolution. The surface generated by the perimeter of the curve is known as surface of revolution and the volume generated by the area is called volume of revolution.     For example, a right angled triangle when revolved about one of its sides (forming the right angle) generates a right circular cones.     (1) Volumes of solids of revolution     (i) The volume of the solid generated by the revolution, about the x-axis, of the area bounded by the curve \[y=f(x),\]  the ordinates at \[x=a,\,x=b\] and the x-axis is equal to \[\pi \int_{a}^{b}{{{y}^{2\,}}\,dx}\].            (ii) The revolution of the area lying between the curve \[x=f(y)\] the y-axis and the lines \[y=a\] and \[y=b\] is given by (interchanging \[x\] and \[y\] in the above formulae) \[\int_{a}^{b}{\pi \,{{x}^{2\,}}}\,dy\].     (iii) If the equation of the generating curve be given by \[x={{f}_{1}}(t)\] and \[y={{f}_{2}}(t)\] and it is revolved about x-axis, then the formula corresponding to \[\int_{a}^{b}{\pi \,{{y}^{2\,}}\,dx}\] becomes \[\int_{{{t}_{1}}}^{{{t}_{2}}}{\pi {{\{{{f}_{2}}(t)\}}^{2}}\,d\,\{{{f}_{1}}(t)\}}\],     where \[{{f}_{1}}\] and \[{{f}_{2}}\] are the values of t corresponding to \[x=a\]  and  \[x=b\].     (2) Area of surfaces of revolution     (i) The curved surface of the solid generated by the revolution, about the x-axis, of the area bounded by the curve \[y=f(x)\], the ordinates at \[x=a,\,\,x=b\] and the x-axis is equal to \[2\pi \int_{x=a}^{x=b}{\,\,\,y\,ds}\].     (ii) If the arc of the curve \[y=f(x)\] revolves about y-axis, then the area of the surface of revolution (between proper limits) \[=2\pi \int_{{}}^{{}}{x\,ds,}\] where \[ds=\sqrt{1+{{\left( \frac{dy}{dx} \right)}^{2}}}\,dx\].     (iii) If the equation of the curve is given in the parametric form \[x={{f}_{1}}(t)\] and \[y={{f}_{2}}(t)\], and the curve revolves about x-axis, then we get the area of the surface of revolution\[=2\pi \int_{t={{t}_{1}}}^{t={{t}_{2}}}{yds\,}\]     \[=2\pi \int_{t={{t}_{1}}}^{t={{t}_{2}}}{\,{{f}_{2}}(t)ds}\]\[=2\pi \int_{{{t}_{1}}}^{{{t}_{2}}}{{{f}_{2}}(t)\sqrt{\left\{ {{\left( \frac{dx}{dt} \right)}^{2}}+{{\left( \frac{dy}{dt} \right)}^{2}} \right\}}\,dt}\],     where \[{{t}_{1}}\] and \[{{t}_{2}}\] are the values of the parameter corresponding to \[x=a\] and \[x=b\].     (3) Volume and surface of the frustum of a cone : If \[{{r}_{1}},\,{{r}_{2}}\] be the radii of the circular ends and k is the distance between centres of circular ends and l be the slant height, then     (i) Volume of frustum of cone \[=\frac{\pi k}{3}(r_{1}^{2}+{{r}_{1}}{{r}_{2}}+r_{2}^{2})\]     (ii) Curved surface area of frustum of cone \[=\pi ({{r}_{1}}+{{r}_{2}})\,l\]     (iii) Whole surface area of frustum of cone     \[=\pi ({{r}_{1}}+{{r}_{2}})\,l\,+\pi \,r_{1}^{2}+\pi r_{2}^{2}\].   (4) Volume and surface of the frustum of a sphere : Let the thickness of the frustum of sphere is k and radii of the circular ends of the frustum are \[{{r}_{1}}\] and \[{{r}_{2}}\], then     (i) Volume of the frustum of sphere \[=\frac{\pi k}{6}(3r_{1}^{2}+3r_{2}^{2}+{{k}^{2}})\]     (ii) Curved surface area more...