| A 1 | B 2 | C 3 | D 4 | E 5 | F 6 | G 7 | H 8 | I 9 | J 10 | K 11 | L 12 | M 13 |
| N 14 | O 15 | P 16 | Q 17 | R 18 | S 19 | T 20 | U 21 | V 22 | W 23 | X 24 | Y 25 | Z 26 |
| Z 1 | Y 2 | X 3 | W 4 | V 5 | U 6 | T 7 | S 8 | R 9 | Q 10 | P 11 | O 12 | N 13 |
| M 14 | L 15 | K 16 | J 17 | I 18 | H 19 | G 20 | F 21 | E 22 | D 23 | C 24 | B 25 | A 26 |
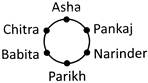
| Son of father or mother | Brother | ||||||||||
| Daughter of father or mother | Sister | ||||||||||
| Brother of father | Uncle | ||||||||||
| Brother of mother | Maternal Uncle | ||||||||||
| Sister of father | Aunt | ||||||||||
| Sister of Mother | Aunt | ||||||||||
| Father of father | Grandfather | ||||||||||
| Father of father of father | Great grandfather | ||||||||||
| Father of grandfather | Great grandfather | ||||||||||
| Mother of father | Grandmother | ||||||||||
| Mother of mother of father | Great grandmother | ||||||||||
| Mother of grandmother | Great grandmother | ||||||||||
| Father of mother | Maternal Grandfather | ||||||||||
| Father of father of mother | Great Maternal grandfather | ||||||||||
| Father of maternal grandmother | Great Maternal grandfather | ||||||||||
| Mother of mother | Maternal grandmother | ||||||||||
| Mother of mother of mother |
Great Maternal grandmother more...
Direction Sense Test
Concept of Direction: In general we make our concept of direction after seeing the position of the Sun. It is an universal truth that Sun rises in the East and goes down in the West. Thus, when we stand facing sunrise our front is called East, and our back is called west. At this position our left hand is in the northward and the right hand is in the southward. Let us see the following direction map to make the concept more clear.
Direction Map:
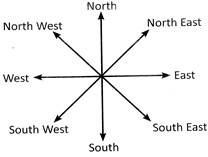 Note: On paper North is always on the top while South is always at the bottom.
Concept of Turn
Left turn = Anti clockwise turn
Right turn = Clockwise turn
Let us understand it through pictorial presentation:
(i)
Note: On paper North is always on the top while South is always at the bottom.
Concept of Turn
Left turn = Anti clockwise turn
Right turn = Clockwise turn
Let us understand it through pictorial presentation:
(i) 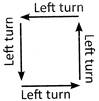 (ii) (ii)  (iii)
(iii) 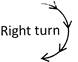 (iv) (iv) 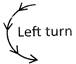 Important Points Regarding Directions
Important Points Regarding Directions
Syllogism
Introduction: Items based on Logical Reasoning are indispensable feature of all competitive examinations these days to test a candidate’s basic intelligence and aptitude. Syllogism is an important section of logical reasoning and hence a working knowledge of its rules is required on the part of the candidate. The term syllogism means inference or deduction drawn from the given statements.
The questions of syllogism can be solved with the help of Venn-diagrams and some rule devised with the help of analytical ability. Some people are of the opinion that Venn-diagram can be of great use for solving questions of syllogism. No doubt a few questions can be solved with the help of Venn-diagrams but van-diagrams alone do not help the students to solve variety of questions of syllogism. Even common sense also will not be much help in working out certain working out certain difficult type of questions. Only the basic concepts and rules, which have a bearing on reasoning faculty could alone help. We have discussed these rule with illustrations throughout the chapter. To proceed further for the study of rules, we must first know some terminology used in syllogism.
Proposition
Proposition, also know a premises, is a grammatical sentence which comprises a subject, a Predicate and a copula. A subject is that which affirms or denies a fact. Predicate is a terms which states something about a subject and copula establishes relationship between the subject and the predicate.
Example: I. All
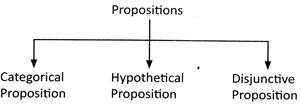 (a) Categorical Proposition: In categorical propositions, there exists a relationship between the subject and the predicate without any condition. It means predicate is either affirmation or denial of the subject unconditionally.
Examples: I. All cups are plates.
II. No Girl is boy.
(b) Hypothetical Proposition: In a hypothetical proposition, relationship between subject and predicate is asserted conditionally.
Examples: I. If it rains, he will not come
II. If he comes, I will accompany him.
(c) Disjunctive Proposition: In a disjunctive proposition, the assertion is of alteration.
Examples: I. Either he is honest or he is loyal.
II. Either he is educated or he is illiterate.
Keeping in view the existing pattern of syllogism in competitive examinations we are concerned only with the categorical type of proposition.
Types of Categorical Proposition
Categorical propositions have been classified on the basis of quality and quantity of the propositions. Quality denotes whether the proposition is affirmative or more...
(a) Categorical Proposition: In categorical propositions, there exists a relationship between the subject and the predicate without any condition. It means predicate is either affirmation or denial of the subject unconditionally.
Examples: I. All cups are plates.
II. No Girl is boy.
(b) Hypothetical Proposition: In a hypothetical proposition, relationship between subject and predicate is asserted conditionally.
Examples: I. If it rains, he will not come
II. If he comes, I will accompany him.
(c) Disjunctive Proposition: In a disjunctive proposition, the assertion is of alteration.
Examples: I. Either he is honest or he is loyal.
II. Either he is educated or he is illiterate.
Keeping in view the existing pattern of syllogism in competitive examinations we are concerned only with the categorical type of proposition.
Types of Categorical Proposition
Categorical propositions have been classified on the basis of quality and quantity of the propositions. Quality denotes whether the proposition is affirmative or more...
Statement and Conclusion
Conclusion: Conclusions are inferences that can be drawn on the basis of the information given in the statement.
In these type of questions, a candidate is asked to decide whether a given inference follows or not in the light of the given statement or passage. For example,
Shravan – Let’s go to a restaurant.
Prakash – I have only Rs. 100.
What is your conclusion? – Shravan and Prakash cannot go to a restaurant. But why? Because nothing comes in Rs. 100 in a restaurant. But how do you know this? You don’t. You should keep in mind that never bring outside information into your reading of a decision making problem. Let’s understand how should we reach a conclusion. For this, follow the simple rules given below:
Rule 1
Don’t assume information, facts unless it is a universal truth.
Example 1:
Statement: People should not give false information to an officer of law.
Conclusion: They should be honest.
Explanation: The conclusion here is based on universal accepted fact that “honesty is the best policy’. So, it follows the statement.
Rule 2
A probably true conclusion has no place and you should treat that as ‘does not follow’.
Example 2:
Statement: If we bring black money back from abroad, it will lead to country’s development.
Conclusion: Black money will help in funding our ongoing development projects.
Explanation: Here, the conclusion may be true and may not be true. So, it is a case of “probable true’ conclusions.
Hence, it does not follow the statement.
Rule 3
Make sure you are not bringing outside information into your questions.
Example 3:
Statement: A player should have the capacity to deal with pressure and control aggression.
Conclusion: Mary Kom, who is a great boxer, has all the above qualities.
Explanation: In the above conclusion, the author is bringing outside information (about Mary Kom), so it does not follow the statement.
Rule 4
Pay attention to the keywords such as - ‘only’, ‘any’ ‘if and only if, ‘either’, ‘neither’, ‘all’, ‘must’, ‘never’, ‘always’ etc.
Example 4:
Statement: Parents are ready to pay any price for admission in a good public school for their children.
Conclusion: All the parents are well-off these days.
Explanation: Since all parents are not very well off, so the conclusion is not true / use of all makes it invalid. If ‘some’ would have been used, instead of ‘all’ then it might have been true.
Rule 5
For any new scheme, policy, even for an organisation which has been newly introduced, it can be concluded that there is a need for that scheme, or policy or an organisation. It can also be concluded that people will welcome it and there are all the essential resources available for its execution and also the people more...
Diagrammatic Puzzles
In these problems one has to count the geometrical figures in a given complex figure. A little bit of systematic approach is needed to get the correct number of the asked figure. The shape of geometrical figures must be clear in mind.
Example:
1. How many triangles are there in the figure given below?
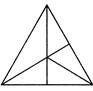 (a) 11 (b) 12
(c) 9 (d) 10
Ans. (b)
Explanation: The main triangle is: ABC - i.e. –1 triangle the simplest triangles are: ABE, AED, EBF, EDC and EFC i.e. -5 triangles
The triangle divided into two parts are: ABF, ABD, AEC and EBC i.e. - 4 triangles
Other triangles are: AFC and DBC i.e. - 2 triangles
So, the total number of triangles is \[1+5+4+2=12\]
(a) 11 (b) 12
(c) 9 (d) 10
Ans. (b)
Explanation: The main triangle is: ABC - i.e. –1 triangle the simplest triangles are: ABE, AED, EBF, EDC and EFC i.e. -5 triangles
The triangle divided into two parts are: ABF, ABD, AEC and EBC i.e. - 4 triangles
Other triangles are: AFC and DBC i.e. - 2 triangles
So, the total number of triangles is \[1+5+4+2=12\]
 2. The maximum number of squares in the figure is
2. The maximum number of squares in the figure is
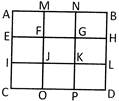 more... more...
Complete of Incomplete Pattern
Introduction: This pattern are developed to judge your ability to comprehend geometric figures and diagrams. There also test your skills in perceiving the structure of a design and identifying the part missing in the main figure from the answer choices given, in the given figure a portion is left blank or incomplete.
In this type of problems, a figure or a matrix, containing a set of figures following a particular sequence or pattern is given, in which a part, generally a quarter is left blank. This problem figure is followed by four alternative figures. The candidate is required to select the one which best fits into the blank space of problem figure so as to complete the original pattern
Example:
1. Which one of the alternative figures will complete the figure pattern?
Pattern
 Ans. (b)
Alternative figures
(a)
Ans. (b)
Alternative figures
(a) 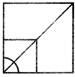 (b) (b) 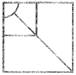 (c)
(c) 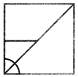 (d) (d)  Ans. (b)
Explanation: Observe that this figure has a square, a circle in the center and diagonal lines radiating from the circle. So, the complete figure will look like this:
Ans. (b)
Explanation: Observe that this figure has a square, a circle in the center and diagonal lines radiating from the circle. So, the complete figure will look like this:
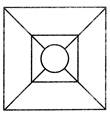 2. Which one of the alternative figures will complete the figure pattern?
2. Which one of the alternative figures will complete the figure pattern?
 Ans. (a)
Alternative figures
(a)
Ans. (a)
Alternative figures
(a) 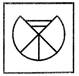 (b) (b) 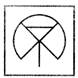 (c)
(c)  (d) (d) 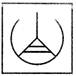 Explanation: Observe that in this figure the centre points of the circles are joined by straight lines. The line ends are split into three. Two parallel lines inside each circle are touching the striaght lines. So, the complete figure will look like this:
Explanation: Observe that in this figure the centre points of the circles are joined by straight lines. The line ends are split into three. Two parallel lines inside each circle are touching the striaght lines. So, the complete figure will look like this:
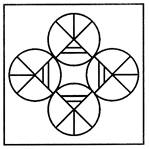 3. Which one of the alternative figures will complete the figure pattern?
Pattern
3. Which one of the alternative figures will complete the figure pattern?
Pattern  more... more... 12th ClassCurrent Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |