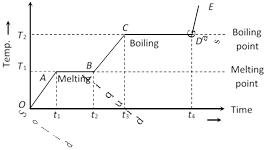
 (1) In the region OA temperature of solid is changing with time so,\[Q=m{{c}_{S}}\Delta T\]\[\Rightarrow \]\[P\,\Delta t=m{{c}_{S}}\Delta T\][as \[Q=P\Delta t\]]
But as \[(\Delta T/\Delta t)\] is the slope of temperature-time curve
\[{{c}_{s}}\propto \frac{1}{\text{Slope of line }OA}\]
i.e. specific heat (or thermal capacity) is inversely proportional to the slope of temperature-time curve.
(2) In the region AB temperature is constant, so it represents change of state, i.e., melting of solid with melting point \[{{T}_{1}}\]. At A melting starts and at B all solid is converted into liquid. So between A and B substance is partly solid and partly liquid. If \[{{L}_{F}}\] is the latent heat of fusion. \[Q=m{{L}_{F}}\]
or \[{{L}_{F}}=\frac{P({{t}_{2}}-{{t}_{1}})}{m}\] [as \[Q=P({{t}_{2}}-{{t}_{1}})\]]
or \[{{L}_{F}}\propto \] length of line AB
i.e. Latent heat of fusion is proportional to the length of line of zero slope. [In this region specific heat \[\propto \]\[\frac{1}{\tan 0}=\infty \]]
(3) In the region BC temperature of liquid increases so specific heat (or thermal capacity) of liquid will be inversely proportional to the slope of line BC
i.e., \[{{c}_{L}}\propto \frac{1}{\text{Slope of line }B\text{C}}\]
(4) In the region CD temperature is constant, so it represents the change of state, i.e., boiling with boiling point \[{{T}_{2}}\]. At C all substance is in liquid state while at D in vapour state and between C and D partly liquid and partly gas. The length of line CD is proportional to latent heat of vaporisation
i.e., \[{{L}_{V}}\propto \] Length of line CD [In this region specific heat\[\propto \frac{1}{\tan 0}=\infty \]]
(5) The line DE represents gaseous state of substance with its temperature increasing linearly with time. The reciprocal of slope of line will be proportional to specific heat or thermal capacity of substance in vapour state.
(1) In the region OA temperature of solid is changing with time so,\[Q=m{{c}_{S}}\Delta T\]\[\Rightarrow \]\[P\,\Delta t=m{{c}_{S}}\Delta T\][as \[Q=P\Delta t\]]
But as \[(\Delta T/\Delta t)\] is the slope of temperature-time curve
\[{{c}_{s}}\propto \frac{1}{\text{Slope of line }OA}\]
i.e. specific heat (or thermal capacity) is inversely proportional to the slope of temperature-time curve.
(2) In the region AB temperature is constant, so it represents change of state, i.e., melting of solid with melting point \[{{T}_{1}}\]. At A melting starts and at B all solid is converted into liquid. So between A and B substance is partly solid and partly liquid. If \[{{L}_{F}}\] is the latent heat of fusion. \[Q=m{{L}_{F}}\]
or \[{{L}_{F}}=\frac{P({{t}_{2}}-{{t}_{1}})}{m}\] [as \[Q=P({{t}_{2}}-{{t}_{1}})\]]
or \[{{L}_{F}}\propto \] length of line AB
i.e. Latent heat of fusion is proportional to the length of line of zero slope. [In this region specific heat \[\propto \]\[\frac{1}{\tan 0}=\infty \]]
(3) In the region BC temperature of liquid increases so specific heat (or thermal capacity) of liquid will be inversely proportional to the slope of line BC
i.e., \[{{c}_{L}}\propto \frac{1}{\text{Slope of line }B\text{C}}\]
(4) In the region CD temperature is constant, so it represents the change of state, i.e., boiling with boiling point \[{{T}_{2}}\]. At C all substance is in liquid state while at D in vapour state and between C and D partly liquid and partly gas. The length of line CD is proportional to latent heat of vaporisation
i.e., \[{{L}_{V}}\propto \] Length of line CD [In this region specific heat\[\propto \frac{1}{\tan 0}=\infty \]]
(5) The line DE represents gaseous state of substance with its temperature increasing linearly with time. The reciprocal of slope of line will be proportional to specific heat or thermal capacity of substance in vapour state. | Condition | Temperature of mixture |
| If bodies are of same material i.e. \[{{c}_{1}}={{c}_{2}}\] | \[{{\theta }_{mix}}=\frac{{{m}_{1}}{{\theta }_{1}}+{{m}_{2}}{{\theta }_{2}}}{{{m}_{1}}+{{m}_{2}}}\] |
| If bodies are of same mass \[{{m}_{1}}={{m}_{2}}\] | \[{{\theta }_{mix}}=\frac{{{\theta }_{1}}{{c}_{1}}+{{\theta }_{2}}{{c}_{2}}}{{{c}_{1}}+{{c}_{2}}}\] |
| If \[{{m}_{1}}={{m}_{2}}\] and \[{{c}_{1}}={{c}_{2}}\] | \[{{\theta }_{mix}}=\frac{{{\theta }_{1}}+{{\theta }_{2}}}{2}\] |
 Whenever heat is converted into mechanical work or mechanical work is converted into heat, then the ratio of work done to heat produced always remains constant. i.e. \[W\propto Q\] or \[\frac{W}{Q}=J\]
This is Joule's law and J is called mechanical equivalent of heat.
(1) From W = JQ if Q = 1 then J = W. Hence the amount of work done necessary to produce unit amount of heat is defined as the mechanical equivalent of heat.
(2) J is neither a constant, nor a physical quantity rather it is a conversion factor which used to convert Joule or erg into calorie or kilo calories vice-versa.
(3) Value of \[J=4.2\,\frac{Joule}{cal}=4.2\times {{10}^{7}}\frac{erg}{cal}\]
\[=4.2\times {{10}^{3}}\frac{Joule}{kcal}\].
(4) When water in a stream falls from height h, then its potential energy is converted into heat and temperature of water rises slightly.
From \[W=JQ\] \[\Rightarrow \] mgh = J (mc \[\Delta \theta \])
[where m = Mass of water, c = Specific heat of water, \[\Delta \theta =\] temperature rise]
\[\Rightarrow \] Rise in temperature \[\Delta \theta =\frac{gh}{Jc}{}^\circ C\]
(5) The kinetic energy of a bullet fired from a gun gets converted into heat on striking the target. By this heat the temperature of bullet increases by\[\Delta \theta \].
From W = JQ \[\Rightarrow \] \[\frac{1}{2}m{{v}^{2}}=J(\,m\,s\,\Delta \theta )\]
[where m = Mass of the bullet, v = Velocity of the bullet, c = Specific heat of the bullet]
\[\Rightarrow \] Rise in temperature \[\Delta t=\frac{{{v}^{2}}}{2Jc}{}^\circ C\]
If the temperature of bullet rises upto the melting point of the bullet and bullet melts then.
From \[W=J({{Q}_{Temperature\text{ }change}}+{{Q}_{Phase\text{ }change}})\]
\[\Rightarrow \] \[\frac{1}{2}m{{v}^{2}}=J(mc\,\Delta \theta +mL)\]; L = Latent heat of bullet
\[\Rightarrow \] Rise in temperature \[\Delta \theta =\left[ \frac{\left( \frac{{{v}^{2}}}{2J}-L \right)}{c} \right]\,{}^\circ C\]
(6) If m kg ice-block falls down through some height (h) and melts partially (m' kg) then its potential energy gets converted into heat of melting.
From W = JQ \[\Rightarrow \] \[mgh=J\,m'L\] \[\Rightarrow \] \[h=\frac{m'}{m}\left( \frac{JL}{g} \right)\]
If ice-block melts completely then \[m'=m\Rightarrow h=\frac{JL}{g}meter\]
Whenever heat is converted into mechanical work or mechanical work is converted into heat, then the ratio of work done to heat produced always remains constant. i.e. \[W\propto Q\] or \[\frac{W}{Q}=J\]
This is Joule's law and J is called mechanical equivalent of heat.
(1) From W = JQ if Q = 1 then J = W. Hence the amount of work done necessary to produce unit amount of heat is defined as the mechanical equivalent of heat.
(2) J is neither a constant, nor a physical quantity rather it is a conversion factor which used to convert Joule or erg into calorie or kilo calories vice-versa.
(3) Value of \[J=4.2\,\frac{Joule}{cal}=4.2\times {{10}^{7}}\frac{erg}{cal}\]
\[=4.2\times {{10}^{3}}\frac{Joule}{kcal}\].
(4) When water in a stream falls from height h, then its potential energy is converted into heat and temperature of water rises slightly.
From \[W=JQ\] \[\Rightarrow \] mgh = J (mc \[\Delta \theta \])
[where m = Mass of water, c = Specific heat of water, \[\Delta \theta =\] temperature rise]
\[\Rightarrow \] Rise in temperature \[\Delta \theta =\frac{gh}{Jc}{}^\circ C\]
(5) The kinetic energy of a bullet fired from a gun gets converted into heat on striking the target. By this heat the temperature of bullet increases by\[\Delta \theta \].
From W = JQ \[\Rightarrow \] \[\frac{1}{2}m{{v}^{2}}=J(\,m\,s\,\Delta \theta )\]
[where m = Mass of the bullet, v = Velocity of the bullet, c = Specific heat of the bullet]
\[\Rightarrow \] Rise in temperature \[\Delta t=\frac{{{v}^{2}}}{2Jc}{}^\circ C\]
If the temperature of bullet rises upto the melting point of the bullet and bullet melts then.
From \[W=J({{Q}_{Temperature\text{ }change}}+{{Q}_{Phase\text{ }change}})\]
\[\Rightarrow \] \[\frac{1}{2}m{{v}^{2}}=J(mc\,\Delta \theta +mL)\]; L = Latent heat of bullet
\[\Rightarrow \] Rise in temperature \[\Delta \theta =\left[ \frac{\left( \frac{{{v}^{2}}}{2J}-L \right)}{c} \right]\,{}^\circ C\]
(6) If m kg ice-block falls down through some height (h) and melts partially (m' kg) then its potential energy gets converted into heat of melting.
From W = JQ \[\Rightarrow \] \[mgh=J\,m'L\] \[\Rightarrow \] \[h=\frac{m'}{m}\left( \frac{JL}{g} \right)\]
If ice-block melts completely then \[m'=m\Rightarrow h=\frac{JL}{g}meter\]  (2) Melting (or fusion)/freezing (or solidification) : The phase change of solid to liquid is called melting or fusion. The reverse phenomenon is called freezing or solidification.
(2) Melting (or fusion)/freezing (or solidification) : The phase change of solid to liquid is called melting or fusion. The reverse phenomenon is called freezing or solidification.
 When pressure is applied on ice, it melts. As soon as the pressure is removed, it freezes again. This phenomenon is called regelation.
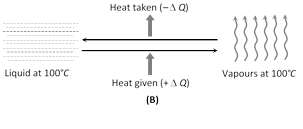
(3) Vaporisation/liquefication (condensation) : The phase change from liquid to vapour is called vaporisation. The reverse transition is called liquefication or condensation.
(4) Sublimation : Sublimation is the conversion of a solid directly into vapours. Sublimation takes place when boiling point is less than the melting point. A block of ice sublimates into vapours on the surface of moon because of very very low pressure on its surface. Heat required to change unit mass of solid directly into vapours at a given temperature is called heat of sublimation at that temperature.
(5) Hoar frost : Direct conversion of vapours into solid is called hoar frost. This process is just reverse of the process of sublimation, e.g., formation of snow by freezing of clouds.
When pressure is applied on ice, it melts. As soon as the pressure is removed, it freezes again. This phenomenon is called regelation.
(3) Vaporisation/liquefication (condensation) : The phase change from liquid to vapour is called vaporisation. The reverse transition is called liquefication or condensation.
(4) Sublimation : Sublimation is the conversion of a solid directly into vapours. Sublimation takes place when boiling point is less than the melting point. A block of ice sublimates into vapours on the surface of moon because of very very low pressure on its surface. Heat required to change unit mass of solid directly into vapours at a given temperature is called heat of sublimation at that temperature.
(5) Hoar frost : Direct conversion of vapours into solid is called hoar frost. This process is just reverse of the process of sublimation, e.g., formation of snow by freezing of clouds.
 (6) Vapour pressure : When the space above a liquid is closed, it soon becomes saturated with vapour and a dynamic equilibrium is established. The pressure exerted by this vapour is called Saturated Vapour Pressure (S.V.P.) whose value depends only on the temperature ? it is independent of any external pressure. If the volume of the space is reduced, some vapour liquefies, but the pressure is unchanged.
A saturated vapour does not obey the gas law whereas the unsaturated vapour obeys them fairly well. However, a vapour differs from a gas in that the former can be liquefied by pressure alone, whereas the latter cannot be liquefied unless it is first cooled.
(7) Boiling : As the temperature of a liquid is increased, the rate of evaporation also increases. A stage is reached when bubbles of vapour start forming in the body of the liquid which rise to the surface and escape. A liquid boils at a temperature at which the S.V.P. is equal to the external pressure.
(6) Vapour pressure : When the space above a liquid is closed, it soon becomes saturated with vapour and a dynamic equilibrium is established. The pressure exerted by this vapour is called Saturated Vapour Pressure (S.V.P.) whose value depends only on the temperature ? it is independent of any external pressure. If the volume of the space is reduced, some vapour liquefies, but the pressure is unchanged.
A saturated vapour does not obey the gas law whereas the unsaturated vapour obeys them fairly well. However, a vapour differs from a gas in that the former can be liquefied by pressure alone, whereas the latter cannot be liquefied unless it is first cooled.
(7) Boiling : As the temperature of a liquid is increased, the rate of evaporation also increases. A stage is reached when bubbles of vapour start forming in the body of the liquid which rise to the surface and escape. A liquid boils at a temperature at which the S.V.P. is equal to the external pressure.
 It is a fast process. The boiling point changes on mixing impurities.
(8) Dew point : It is that temperature at which the mass of water vapour present in a given volume of air is just sufficient to saturate it, i.e. the temperature at which the actual vapour pressure becomes equal to the saturated vapuor pressure.
(9) Humidity : Atmospheric air always contains some more...
It is a fast process. The boiling point changes on mixing impurities.
(8) Dew point : It is that temperature at which the mass of water vapour present in a given volume of air is just sufficient to saturate it, i.e. the temperature at which the actual vapour pressure becomes equal to the saturated vapuor pressure.
(9) Humidity : Atmospheric air always contains some more... 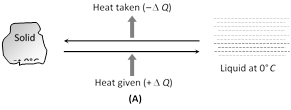
 (iii) In solids, the forces between the molecules are large and the molecules are almost fixed in their positions inside the solid. In a liquid, the forces between the molecules are weaker and the molecules may move freely inside the volume of the liquid. However, they are not able to come out of the surface. In vapours or gases, the intermolecular forces are almost negligible and the molecules may move freely anywhere in the container. When a solid melts, its molecules move apart against the strong molecular attraction. This needs energy which must be supplied from outside. Thus, the internal energy of a given body is larger in liquid phase than in solid phase. Similarly, the internal energy of a given body in vapour phase is larger than that in liquid phase.
(iv) In case of change of state if the molecules come closer, energy is released and if the molecules move apart, energy is absorbed.
(2) Latent heat : The amount of heat required to change the state of the mass m of the substance is written as : Q = mL, where L is the latent heat. Latent heat is also called as Heat of Transformation. It's unit is cal/gm or J/kg and Dimension: \[[{{L}^{2}}{{T}^{-2}}]\]
(i) Latent heat of fusion : The latent heat of fusion is the heat energy required to change 1 kg of the material in its solid state at its melting point to 1 kg of the material in its liquid state. It is also the amount of heat energy released when at melting point 1 kg of liquid changes to 1 kg of solid. For water at its normal freezing temperature or melting point \[({{0}^{o}}C),\] the latent heat of fusion (or latent heat of ice) is \[{{L}_{F}}={{L}_{\text{ice}}}\approx 80\,cal/gm\approx 60\,kJ/mol\approx 336\,kilo\,joule/kg\]
(ii) Latent heat of vaporisation : The latent heat of vaporisation is the heat energy required to change 1 kg of the material in its liquid state at its boiling point to 1 kg of the material in its gaseous state. It is also the amount of heat energy released when 1 kg of vapour changes into 1 kg of liquid. For water at its normal boiling point or condensation temperature \[({{100}^{o}}C),\] the latent heat of vaporisation (latent heat of steam) is \[{{L}_{V}}={{L}_{\text{steam}}}\approx 540\,cal/gm\approx 40.8\,kJ/mol\approx 2260\,kilo\,joule/kg\]
(iii) Latent heat of vaporisation is more than the latent heat of fusion. This is because when a substance gets more...
(iii) In solids, the forces between the molecules are large and the molecules are almost fixed in their positions inside the solid. In a liquid, the forces between the molecules are weaker and the molecules may move freely inside the volume of the liquid. However, they are not able to come out of the surface. In vapours or gases, the intermolecular forces are almost negligible and the molecules may move freely anywhere in the container. When a solid melts, its molecules move apart against the strong molecular attraction. This needs energy which must be supplied from outside. Thus, the internal energy of a given body is larger in liquid phase than in solid phase. Similarly, the internal energy of a given body in vapour phase is larger than that in liquid phase.
(iv) In case of change of state if the molecules come closer, energy is released and if the molecules move apart, energy is absorbed.
(2) Latent heat : The amount of heat required to change the state of the mass m of the substance is written as : Q = mL, where L is the latent heat. Latent heat is also called as Heat of Transformation. It's unit is cal/gm or J/kg and Dimension: \[[{{L}^{2}}{{T}^{-2}}]\]
(i) Latent heat of fusion : The latent heat of fusion is the heat energy required to change 1 kg of the material in its solid state at its melting point to 1 kg of the material in its liquid state. It is also the amount of heat energy released when at melting point 1 kg of liquid changes to 1 kg of solid. For water at its normal freezing temperature or melting point \[({{0}^{o}}C),\] the latent heat of fusion (or latent heat of ice) is \[{{L}_{F}}={{L}_{\text{ice}}}\approx 80\,cal/gm\approx 60\,kJ/mol\approx 336\,kilo\,joule/kg\]
(ii) Latent heat of vaporisation : The latent heat of vaporisation is the heat energy required to change 1 kg of the material in its liquid state at its boiling point to 1 kg of the material in its gaseous state. It is also the amount of heat energy released when 1 kg of vapour changes into 1 kg of liquid. For water at its normal boiling point or condensation temperature \[({{100}^{o}}C),\] the latent heat of vaporisation (latent heat of steam) is \[{{L}_{V}}={{L}_{\text{steam}}}\approx 540\,cal/gm\approx 40.8\,kJ/mol\approx 2260\,kilo\,joule/kg\]
(iii) Latent heat of vaporisation is more than the latent heat of fusion. This is because when a substance gets more... 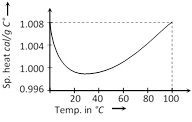 (4) As specific heat of water is very large; by absorbing or releasing large amount of heat its temperature changes by small amount. This is why, it is used in hot water bottles or as coolant in radiators.
(4) As specific heat of water is very large; by absorbing or releasing large amount of heat its temperature changes by small amount. This is why, it is used in hot water bottles or as coolant in radiators. 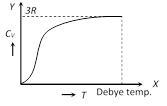 (1) From the graph it is clear that at \[T=0,\,\,{{C}_{V}}\] tends to zero
(2) With rise in temperature, \[{{C}_{V}}\] increases and at a particular temperature (called Debey's temperature) it becomes constant = 3R = 6 cal/mole \[\times \] kelvin = 25 J/mole \[\times \] kelvin
(3) For most of the solids, Debye temperature is close to room temperature.
(4) Dulong and Petit law : Average molar specific heat of all metals at room temperature is constant, being nearly equal to 3R = 6 cal. \[mol{{e}^{-1}}\,{{K}^{-1}}\] = 25 J \[mol{{e}^{-1}}\,{{K}^{-1}}\], where R is gas constant for one mole of the gas. This statement is known as Dulong and Petit law.
(5) Debey's law : It was observed that at very low temperature molar specific heat \[\propto {{T}^{3}}\] exception are Sn, Pb and Pt)
(6) Specific heat of ice : In C.G.S. \[{{c}_{\text{ice}}}=0.5\,\frac{cal}{gm\times {}^\circ C}\]
In S.I. \[{{c}_{ice}}==500\,\frac{cal}{kg\times {}^\circ C}=2100\,\frac{Joule}{kg\times {}^\circ C}\].
Specific heat of some solids at room temperature and atmospheric pressure
(1) From the graph it is clear that at \[T=0,\,\,{{C}_{V}}\] tends to zero
(2) With rise in temperature, \[{{C}_{V}}\] increases and at a particular temperature (called Debey's temperature) it becomes constant = 3R = 6 cal/mole \[\times \] kelvin = 25 J/mole \[\times \] kelvin
(3) For most of the solids, Debye temperature is close to room temperature.
(4) Dulong and Petit law : Average molar specific heat of all metals at room temperature is constant, being nearly equal to 3R = 6 cal. \[mol{{e}^{-1}}\,{{K}^{-1}}\] = 25 J \[mol{{e}^{-1}}\,{{K}^{-1}}\], where R is gas constant for one mole of the gas. This statement is known as Dulong and Petit law.
(5) Debey's law : It was observed that at very low temperature molar specific heat \[\propto {{T}^{3}}\] exception are Sn, Pb and Pt)
(6) Specific heat of ice : In C.G.S. \[{{c}_{\text{ice}}}=0.5\,\frac{cal}{gm\times {}^\circ C}\]
In S.I. \[{{c}_{ice}}==500\,\frac{cal}{kg\times {}^\circ C}=2100\,\frac{Joule}{kg\times {}^\circ C}\].
Specific heat of some solids at room temperature and atmospheric pressure
| Substance | Specific heat \[\mathbf{(J-k}{{\mathbf{g}}^{\mathbf{-1}}}\,{{\mathbf{K}}^{\mathbf{-1}}}\mathbf{)}\] | Molar specific heat \[\mathbf{(J-g}\,\,\mathbf{mol}{{\mathbf{e}}^{\mathbf{-1}}}\,{{\mathbf{K}}^{\mathbf{-1}}}\mathbf{)}\] |
| Aluminium | 900.0 | 24.4 |
| Copper | 386.4 | 24.5 |
| Silver | 236.1 | 25.5 |
| Lead | 127.7 | 26.5 |
| Tungsten | 134.4 | 24.9 |
You need to login to perform this action.
You will be redirected in
3 sec
