Current Affairs JEE Main & Advanced

(1) It is a statement of conservation of energy in thermodynamical process. (2) According to it heat given to a system \[(\Delta Q)\] is equal to the sum of increase in its internal energy \[(\Delta U)\] and the work done \[(\Delta W)\] by the system against the surroundings. \[\Delta Q=\,\Delta U+\Delta W\] (3) It makes no distinction between work and heat as according to it the internal energy (and hence temperature) of a system may be increased either by adding heat to it or doing work on it or both. (4) \[\Delta Q\] and \[\Delta W\] are the path functions but \[\Delta U\] is the point function. (5) In the above equation all three quantities \[\Delta Q,\,\Delta U\]and \[\Delta W\] must be expressed either in Joule or in calorie. (6) The first law introduces the concept of internal energy. (7) Limitation : First law of thermodynamics does not indicate the direction of heat transfer. It does not tell anything about the conditions, under which heat can be transformed into work and also it does not indicate as to why the whole of heat energy cannot be converted into mechanical work continuously.   Useful sign convention in thermodynamics

Quantity	Sign	Condition
\[\Delta Q\]	+	When heat is supplied to a system
	?	When heat is drawn from the system
\[\Delta W\]	+	When work done by the gas (expansion)
	?	When work done on the gas (compression)
\[\Delta U\]	+	With temperature rise, internal energy increases
	?	With temperature fall, internal energy decreases

   

(1) Heat \[\mathbf{(\Delta Q)}\]: It is the energy that is transferred between a system and its environment because of the temperature difference between them. (i) Heat is a path dependent quantity e.g. Heat required to change the temperature of a given gas at a constant pressure is different from that required to change the temperature of same gas through same amount at constant volume. (ii) For gases when heat is absorbed and temperature changes \[\Rightarrow \]\[\Delta Q=\mu C\Delta T\] At constant pressure \[{{(\Delta Q)}_{P}}=\mu {{C}_{P}}\Delta T\] At constant volume \[{{(\Delta Q)}_{V}}=\mu {{C}_{V}}\Delta T\] (2) Internal energy (U) : Internal energy of a system is the energy possessed by the system due to molecular motion and molecular configuration. The energy due to molecular motion is called internal kinetic energy \[{{U}_{K}}\] and that due to molecular configuration is called internal potential energy \[{{U}_{P}}\] i.e. Total internal energy \[U={{U}_{K}}+{{U}_{P}}\] (i) For an ideal gas, as there is no molecular attraction \[{{U}_{p}}=0\] i.e. internal energy of an ideal gas is totally kinetic and is given by \[U={{U}_{K}}=\frac{3}{2}\mu RT\] and change in internal energy \[\Delta U=\frac{3}{2}\mu R\,\Delta T\] (ii) In case of gases whatever be the process \[\Delta U=\mu \frac{f}{2}R\Delta T\]\[=\mu {{C}_{V}}\Delta T\]\[=\mu \frac{R}{(\gamma -1)}\Delta T=\frac{\mu \,R({{T}_{f}}-{{T}_{i}})}{\gamma -1}\] \[=\frac{\mu R{{T}_{f}}-\mu R{{T}_{i}}}{\gamma -1}\]\[=\frac{({{P}_{f}}{{V}_{f}}-{{P}_{i}}{{V}_{i}})}{\gamma -1}\] (iii) Change in internal energy does not depend on the path of the process. So it is called a point function i.e. it depends only on the initial and final states of the system, i.e. \[\Delta U={{U}_{f}}-{{U}_{i}}\] (3) Work \[\mathbf{(\Delta W)}\]: Suppose a gas is confined in a cylinder that has a movable piston at one end. 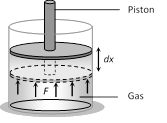If P be the pressure of the gas in the cylinder, then force exerted by the gas on the piston of the cylinder F = PA (A = Area of cross-section of piston) When the piston is pushed outward an infinitesimal distance dx, the work done by the gas \[dW=F.dx=P(A\,dx)=P\,dV\] For a finite change in volume from \[{{V}_{i}}\] to \[{{V}_{f}}\] Total amount of work done \[W=\int_{\,Vi}^{\,{{V}_{f}}}{P\,dV}=P({{V}_{f}}-{{V}_{i}})\] (i) If we draw indicator diagram, the area bounded by PV-graph and volume axis represents the work done Work = Area \[=P({{V}_{2}}{{V}_{1}})\] 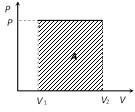Work \[=\int_{\,{{V}_{1}}}^{{{V}_{2}}}{PdV}=P({{V}_{2}}-{{V}_{1}})\] 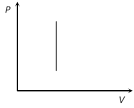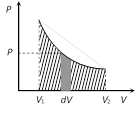Work = 0 Work = Area of the shown trapezium \[=\frac{1}{2}({{P}_{1}}+{{P}_{2}})\,({{V}_{2}}-{{V}_{1}})\] 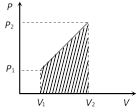(ii) From  \[\Delta W=P\Delta V=P({{V}_{f}}-{{V}_{i}})\] If system expands against some external force then \[{{V}_{f}}>{{V}_{i}}\] \[\Rightarrow \] \[\Delta W=\] positive If system contracts because of external force then \[{{V}_{f}}

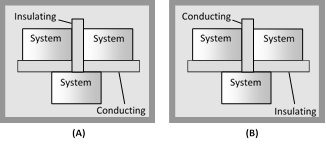If systems A and B are each in thermal equilibrium with a third system C, then A and B are in thermal equilibrium with each other. (1) The zeroth law leads to the concept of temperature. All bodies in thermal equilibrium must have a common property which has the same value for all of them. This property is called the temperature. (2) The zeroth law came to light long after the first and seconds laws of thermodynamics had been discovered and numbered. It is so named because it logically precedes the first and second laws of thermodynamics.  

(1) Thermodynamic system (i) It is a collection of an extremely large number of atoms or molecules (ii) It is confined with in certain boundaries. (iii) Anything outside the thermodynamic system to which energy or matter is exchanged is called its surroundings. (iv) Thermodynamic system may be of three types (a) Open system : It exchange both energy and matter with the surrounding. (b) Closed system : It exchange only energy (not matter) with the surroundings. (c) Isolated system : It exchange neither energy nor matter with the surrounding. 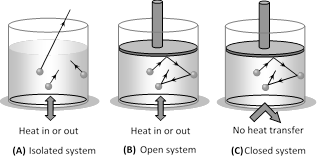(2) Thermodynamic variables and equation of state : A thermodynamic system can be described by specifying its pressure, volume, temperature, internal energy and the number of moles. These parameters are called thermodynamic variables. The relation between the thermodynamic variables (P, V, T) of the system is called equation of state. For \[\mu \] moles of an ideal gas, equation of state is \[PV=\mu RT\] and for 1 mole of an it ideal gas is PV = RT (3) Thermodynamic equilibrium : In steady state thermodynamic variables are independent of time and the system is said to be in the state of thermodynamic equilibrium. For a system to be in thermodynamic equilibrium, the following conditions must be fulfilled. (i) Mechanical equilibrium : There is no unbalanced force between the system and its surroundings. (ii) Thermal equilibrium : There is a uniform temperature in all parts of the system and is same as that of surrounding. (iii) Chemical equilibrium : There is a uniform chemical composition through out the system and the surrounding. (4) Thermodynamic process : The process of change of state of a system involves change of thermodynamic variables such as pressure P, volume V and temperature T of the system. The process is known as thermodynamic process. Some important processes are (i) Isothermal process : Temperature remain constant (ii) Adiabatic process : No transfer of heat (iii) Isobaric process : Pressure remains constant (iv) Isochoric (isovolumic process) : Volume remains constant (v) Cyclic and non-cyclic process : Incyclic process Initial and final states are same while in non-cyclic process these states are different. (vi) Reversible and irreversible process : (5) Indicator diagram : Whenever the state of a gas (P, V, T) is changed, we say the gaseous system is undergone a thermodynamic process. The graphical representation of the change in state of a gas by a thermodynamic process is called indicator diagram. Indicator diagram is plotted generally in pressure and volume of gas.

  Thermodynamics is a branch of science which deals with exchange of heat energy between bodies and conversion of the heat energy into mechanical energy and vice-versa.

If two non-reactive gases are enclosed in a vessel of volume V. In the mixture \[{{\mu }_{1}}\] moles of one gas are mixed with \[{{\mu }_{2}}\] moles of another gas. If \[{{N}_{A}}\] is Avogadro's number then Number of molecules of first gas \[{{N}_{1}}={{\mu }_{1}}\,{{N}_{A}}\] and number of molecules of second gas \[{{N}_{2}}={{\mu }_{2}}{{N}_{A}}\] (1) Total mole fraction \[\mu =({{\mu }_{1}}+{{\mu }_{2}})\]. (2) If \[{{M}_{1}}\] is the molecular weight of first gas and \[{{M}_{2}}\] that of second gas. Then molecular weight of mixture \[M=\frac{{{\mu }_{1}}{{M}_{1}}+{{\mu }_{2}}{{M}_{2}}}{{{\mu }_{1}}+{{\mu }_{2}}}\] (3) Specific heat of the mixture at constant volume will be   \[{{C}_{{{V}_{mix}}}}=\frac{{{\mu }_{1}}{{C}_{{{V}_{1}}}}+{{\mu }_{2}}{{C}_{{{V}_{2}}}}}{{{\mu }_{1}}+{{\mu }_{2}}}\]\[=\frac{\frac{{{m}_{1}}}{{{M}_{1}}}{{C}_{{{V}_{1}}}}+\frac{{{m}_{2}}}{{{M}_{2}}}{{C}_{{{V}_{2}}}}}{\frac{{{m}_{1}}}{{{M}_{1}}}+\frac{{{m}_{2}}}{{{M}_{2}}}}\] (4) Specific heat of the mixture at constant pressure will be \[{{C}_{{{P}_{mix}}}}=\frac{{{\mu }_{1}}{{C}_{{{P}_{1}}}}+{{\mu }_{2}}{{C}_{{{P}_{2}}}}}{{{\mu }_{1}}+{{\mu }_{2}}}\]\[=\frac{{{\mu }_{1}}\left( \frac{{{\gamma }_{1}}}{{{\gamma }_{1}}-1} \right)R+{{\mu }_{2}}\left( \frac{{{\gamma }_{2}}}{{{\gamma }_{2}}-1} \right)R}{{{\mu }_{1}}+{{\mu }_{2}}}\] \[=\frac{R}{{{\mu }_{1}}+{{\mu }_{2}}}\left[ {{\mu }_{1}}\left( \frac{{{\gamma }_{1}}}{{{\gamma }_{1}}-1} \right)+{{\mu }_{2}}\left( \frac{{{\gamma }_{2}}}{{{\gamma }_{2}}-1} \right) \right]\] \[=\frac{R}{\frac{{{m}_{1}}}{{{M}_{1}}}+\frac{{{m}_{2}}}{{{M}_{2}}}}\left[ \frac{{{m}_{1}}}{{{M}_{1}}}\left( \frac{{{\gamma }_{1}}}{{{\gamma }_{1}}-1} \right)+\frac{{{m}_{2}}}{{{M}_{2}}}\left( \frac{{{\gamma }_{2}}}{{{\gamma }_{2}}-1} \right) \right]\] (5) \[{{\gamma }_{\text{mixture}}}=\frac{{{C}_{{{P}_{mix}}}}}{{{C}_{{{V}_{mix}}}}}=\frac{\frac{({{\mu }_{1}}{{C}_{{{P}_{1}}}}+{{\mu }_{2}}{{C}_{{{P}_{2}}}})}{{{\mu }_{1}}+{{\mu }_{2}}}}{\frac{({{\mu }_{1}}{{C}_{{{V}_{1}}}}+{{\mu }_{2}}{{C}_{{{V}_{2}}}})}{{{\mu }_{1}}+{{\mu }_{2}}}}\] \[=\frac{{{\mu }_{1}}{{C}_{{{P}_{1}}}}+{{\mu }_{2}}{{C}_{{{P}_{2}}}}}{{{\mu }_{1}}{{C}_{{{V}_{1}}}}+{{\mu }_{2}}{{C}_{{{V}_{2}}}}}\]\[=\frac{\left\{ {{\mu }_{1}}\left( \frac{{{\gamma }_{1}}}{{{\gamma }_{1}}-1} \right)R+{{\mu }_{2}}\left( \frac{{{\gamma }_{2}}}{{{\gamma }_{2}}-1} \right)R \right\}}{\left\{ {{\mu }_{1}}\left( \frac{R}{{{\gamma }_{1}}-1} \right)+{{\mu }_{2}}\left( \frac{R}{{{\gamma }_{2}}-1} \right) \right\}}\] \[\therefore \]\[{{\gamma }_{\text{mixture}}}=\frac{\frac{{{\mu }_{1}}{{\gamma }_{1}}}{{{\gamma }_{1}}-1}+\frac{{{\mu }_{2}}{{\gamma }_{2}}}{{{\gamma }_{2}}-1}}{\frac{{{\mu }_{1}}}{{{\gamma }_{1}}-1}+\frac{{{\mu }_{2}}}{{{\gamma }_{2}}-1}}=\frac{{{\mu }_{1}}{{\gamma }_{1}}({{\gamma }_{2}}-1)+{{\mu }_{2}}{{\gamma }_{2}}({{\gamma }_{1}}-1)}{{{\mu }_{1}}({{\gamma }_{2}}-1)+{{\mu }_{2}}({{\gamma }_{1}}-1)}\]  

(1) \[{{C}_{V}}:\] For a gas at temperature T, the internal energy \[U=\frac{f}{2}\mu RT\] \[\Rightarrow \] Change in energy \[\Delta U=\frac{f}{2}\mu R\Delta T\]... (i) Also, as we know for any gas heat supplied at constant volume \[{{(\Delta Q)}_{V}}=\mu {{C}_{V}}\Delta T=\Delta U\]                                ... (ii) From equation (i) and (ii) \[{{C}_{V}}=\frac{1}{2}fR\] (2) \[{{C}_{P}}:\] From the Mayer?s formula \[{{C}_{p}}-{{C}_{v}}=R\] \[\Rightarrow \] \[{{C}_{P}}={{C}_{V}}+R=\frac{f}{2}R+R\]\[=\left( \frac{f}{2}+1 \right)\,R\] (3) Ratio of \[{{C}_{p}}\] and \[{{C}_{v}}\,(\gamma ):\] \[\gamma =\frac{{{C}_{p}}}{{{C}_{v}}}=\frac{\left( \frac{f}{2}+1 \right)R}{\frac{f}{2}R}=1+\frac{2}{f}\] (i) Value of \[\gamma \] is different for monoatomic, diatomic and triatomic gases.\[{{\gamma }_{mono}}=\frac{5}{3}=1.6,\,{{\gamma }_{di}}=\frac{7}{5}=1.4,\,{{\gamma }_{tri}}=\frac{4}{3}=1.33\] (ii) Value of \[\gamma \]  is always more than 1. So we can say that always \[{{C}_{P}}>{{C}_{V}}\].

(1) Out of two principle specific heats of a gas, \[{{C}_{P}}\] is more than \[{{C}_{V}}\] because in case of \[{{C}_{V}},\] volume of gas is kept constant and heat is required only for raising the temperature of one gram mole of the gas through \[{{1}^{o}}C\] or 1 K. Hence no heat, what so ever, is spent in expansion of the gas. It means that heat supplied to the gas increases its internal energy only i.e. \[{{(\Delta Q)}_{V}}=\Delta U=\mu {{C}_{V}}\Delta T\]          ...(i) (2) While in case of \[{{C}_{P}}\] the heat is used in two ways (i) In increasing the temperature of the gas by \[\Delta T\] (ii) In doing work, due to expansion at constant pressure \[(\Delta W)\] So           \[{{(\Delta Q)}_{P}}=\Delta U+\Delta W=\mu \,{{C}_{P}}\Delta T\]                           ...(ii) From equation (i) and (ii)    \[\mu \,{{C}_{P}}\Delta T-\mu \,{{C}_{V}}\Delta T=\Delta W\] \[\Rightarrow \] \[\mu \,\Delta T({{C}_{P}}-{{C}_{V}})=P\Delta V\] \[\Rightarrow \] \[{{C}_{P}}-{{C}_{V}}=\frac{P\Delta V}{\mu \,\Delta T}=R\] [For constant pressure, \[\Delta W=P\Delta V\] also from \[PV=\mu RT,\] \[P\Delta V=\mu R\Delta T\]] This relation is called Mayer?s formula and shows that \[{{C}_{P}}>{{C}_{V}}\] i.e. molar specific heat at constant pressure is greater than that at constant volume.  

The specific heat of gas can have many values, but out of them following two values are very important (1) Specific heat at constant volume \[({{C}_{V}})\] : The specific heat of a gas at constant volume is defined as the quantity of heat required to raise the temperature of unit mass of gas through \[{{1}^{o}}C\] or  1 K when its volume is kept constant, i.e., \[{{c}_{V}}=\frac{{{(\Delta Q)}_{V}}}{m\Delta T}\] If instead of unit mass, 1 mole of gas is considered, the specific heat is called molar specific heat at constant volume and is represented by capital \[{{C}_{V}}\]. \[{{C}_{V}}=M{{c}_{V}}=\frac{M{{(\Delta Q)}_{V}}}{m\Delta T}=\frac{1}{\mu }\frac{{{(\Delta Q)}_{V}}}{\Delta T}\]                \[\left[ \text{As }\mu =\frac{m}{M} \right]\] (2) Specific heat at constant from \[({{C}_{P}})\] : The specific heat of a gas at constant pressure is defined as the quantity of heat required to raise the temperature of unit mass of gas through 1 K when its pressure is kept constant, i.e., \[{{c}_{P}}=\frac{{{(\Delta Q)}_{p}}}{m\Delta T}\] If instead of unit mass, 1 mole of gas is considered, the specific heat is called molar specific heat at constant pressure and is represented by \[{{C}_{P}}\]. \[{{C}_{p}}=M{{C}_{p}}=\frac{M{{(\Delta Q)}_{p}}}{m\Delta T}=\frac{1}{\mu }\frac{{{(\Delta Q)}_{p}}}{\Delta T}\]                \[\left[ \text{As }\mu =\frac{m}{M} \right]\]  

According to this law, for any system in thermal equilibrium, the total energy is equally distributed among its various degree of freedom. And each degree of freedom is associated with energy \[\frac{1}{2}kT\] (where \[k=1.38\times {{10}^{-23}}\,J/K\], T = absolute temperature of the system). (1) At a given temperature T, all ideal gas molecules no  matter what their mass have the same average translational kinetic energy; namely, \[\frac{3}{2}kT.\] When measure the temperature of a gas, we are also measuring the average translational kinetic energy of it' s molecules. (2) At same temperature gases with different degrees of freedom (e.g., He and \[{{H}_{2}}\]) will have different average energy or internal energy namely \[\frac{f}{2}kT.\] (f is different for different gases) (3) Different energies of a system of degree of freedom f are as follows (i) Total energy associated with each molecule  \[=\frac{f}{2}kT\] (ii) Total energy associated with N molecules \[=\frac{f}{2}NkT\] (iii) Total energy associated with \[\mu \] mole \[=\frac{f}{2}RT\] (iv) Total energy associated with \[\mu \] molen \[=\frac{\,f}{2}\mu RT\] (v) Total energy associated with each gram \[=\frac{f}{2}rT\] (iv) Total energy associated with m gram \[=\frac{f}{2}mrT\]