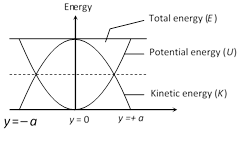
(i) At \[y=0;\,\,U=0\] and \[K=E\]
(ii) At \[y=\pm a;\,\,U=E\] and \[K=0\]
(iii) At \[y=\pm \frac{a}{2}\]; \[U=\frac{E}{4}\]and \[K=\frac{3E}{4}\]
(iv) At \[y=\pm \frac{a}{\sqrt{2}}\]; \[U=K=\frac{E}{2}\] | Graph | Formula | At mean position | At extreme position |
Displacement
|
\[y=a\sin \omega \,t\] | \[y=0\] | \[y=\pm a\] |
Velocity
|
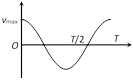
\[v=a\omega \cos \omega \,t\] \[=a\omega \sin (\omega \,t+\frac{\pi }{2})\] or \[v=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\] | \[{{v}_{\max }}=a\omega \] | \[{{v}_{\min }}=0\] |
Acceleration
|
\[A=-a{{\omega }^{2}}\sin \omega \,t\] \[=a{{\omega }^{2}}\sin (\omega \,t+\pi )\] or \[\left| A\, \right|={{\omega }^{2}}y\] | more...
(1) The acceleration of the particle executing S.H.M. at any instant, is defined as the rate of change of its velocity at that instant. So acceleration
\[A=\frac{dv}{dt}=\frac{d}{dt}(a\omega \cos \omega \,t)\]\[=-{{\omega }^{2}}a\sin \omega \,t\]\[=-{{\omega }^{2}}y\] [As \[y=a\sin \omega \,t\]]
(2) In S.H.M. as \[\left| \,\text{Acceleration}\, \right|\,\,={{\omega }^{2}}y\] is not constant. So equations of translatory motion can not be applied.
(3) In S.H.M. acceleration is maximum at extreme position (at \[y=\pm a\]). Hence \[\left| {{A}_{\max }} \right|={{\omega }^{2}}a\] when \[\left| \,\sin \,\omega \,t\, \right|=\text{maximum}=1\] i.e. at \[t=\frac{T}{4}\] or \[\omega t=\frac{\pi }{2}\]. From equation
(ii) \[|{{A}_{\max }}|\,={{\omega }^{2}}a\] when \[y=a\]. (i) In S.H.M. acceleration is minimum at mean position From equation (i) \[{{A}_{\min }}=0\] when \[\sin \omega \,t=0\] i.e. at \[t=0\] or \[t=\frac{T}{2}\] or \[\omega \,t=\pi \]. From equation
(ii) \[{{A}_{\min }}=0\] when \[y=0\] (ii) Acceleration is always directed towards the mean position and so is always opposite to displacement
i.e., \[A\propto -y\]
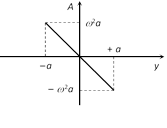Graph between acceleration (A) and displacement (y) is a straight line as shown
Slope of the line \[=-{{\omega }^{2}}\]
(1) Velocity of the particle executing S.H.M. at any instant, is defined as the time rate of change of its displacement at that instant.
(2) In case of S.H.M. when motion is considered from the equilibrium position, displacement \[y=a\sin \omega \,t\]
So \[v=\frac{dy}{dt}=a\omega \cos \omega \,t\]\[=a\omega \sqrt{1-{{\sin }^{2}}\omega \,t}\]\[=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\]
[As \[\sin \omega t=y/a\]]
(3) At mean position or equilibrium position \[(y=0\,\,\text{and }\,\theta =\omega t=0),\] velocity of particle is maximum and it is \[{{v}_{\max }}=a\omega \].
(4) At extreme position \[(y=\pm a\,\,\text{and}\,\,\theta =\omega t=\pi /2),\] velocity of oscillating particle is zero i.e. \[v=0\].
(5) From \[v=\omega \sqrt{{{a}^{2}}-{{y}^{2}}}\]\[\Rightarrow \] \[{{v}^{2}}={{\omega }^{2}}({{a}^{2}}-{{y}^{2}})\]\[\Rightarrow \]\[\frac{{{v}^{2}}}{{{\omega }^{2}}}={{a}^{2}}-{{y}^{2}}\]
\[\Rightarrow \] \[\frac{{{v}^{2}}}{{{a}^{2}}{{\omega }^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]
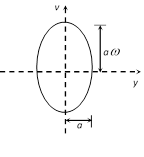This is the equation of ellipse. Hence the graph between v and y is an ellipse.
For \[\omega =1,\] graph between v and y is a circle.
(6) Direction of velocity is either towards or away from mean position depending on the position of particle.
(1) The displacement of a particle executing S.H.M. at an instant is defined as the distance of particle from the mean position at that instant.
(2) Simple harmonic motion is also defined as the projection of uniform circular motion on any diameter of circle of reference.
(3) If the projection is taken on y-axis. then from the figure
\[y=a\sin \omega \,t\]\[=a\sin \frac{2\pi }{T}t\]\[=a\sin 2\pi \,n\,t\]\[=a\sin (\omega \,t\pm \varphi )\]
(i) \[y=a\sin \omega \,t\] when the time is noted from the instant when the vibrating particle is at mean position.
(ii) \[y=a\cos \omega \,t\] when the time is noted from the instant when the vibrating particle is at extreme position.
(iii) \[y=a\sin (\omega \,t\pm \varphi )\] when the vibrating particle is f phase leading or lagging from the mean position.
(4) If the projection of P is taken on X-axis then equations of S.H.M. can be given as \[x=a\cos \,(\omega \,t\pm \varphi )\]\[=a\cos \,\left( \frac{2\pi }{T}t\pm \varphi \right)\]\[=a\cos \,(2\pi n\,t\pm \varphi )\]
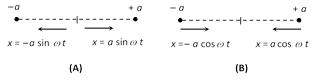(5) Direction of displacement is always away from the equilibrium position, particle either is moving away from or is coming towards the equilibrium position.
(1) Time period (T) : It is the least interval of time after which the periodic motion of a body repeats itself. S.I. unit of time period is second.
(2) Frequency (n) : It is defined as the number of oscillations executed by body per second. S.I unit of frequency is hertz (Hz).
(3) Angular Frequency \[(\omega )\]: Angular frequency of a body executing periodic motion is equal to product of frequency of the body with factor \[2\pi \]. Angular frequency \[\omega =2\pi n\] Its unit is rad/sec.
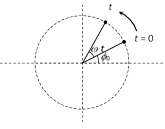
(4) Phase \[(\phi )\]: Phase of a vibrating particle at any instant is a physical quantity, which completely express the position and direction of motion, of the particle at that instant with respect to its mean position.
In oscillatory motion the phase of a vibrating particle is the argument of sine or cosine function involved to represent the generalised equation of motion of the vibrating particle.
\[y=a\sin \theta =a\sin (\omega \,t+{{\varphi }_{0}})\]
here, \[\theta =\omega \,t+{{\varphi }_{0}}\]= phase of vibrating particle.
\[{{\phi }_{0}}=\]Initial phase or epoch. It is the phase of a vibrating particle at \[t=0\].
(1) Same phase : Two vibrating particle are said to be in same phase, if the phase difference between them is an even multiple of \[\pi \] or path difference is an even multiple of \[(\lambda /2)\] or time interval is an even multiple of (T / 2) because 1 time period is equivalent to \[2\pi \] rad or 1 wave length \[(\lambda )\].
(2) Opposite phase : When the two vibrating particles cross their respective mean positions at the same time moving in opposite directions, then the phase difference between the two vibrating particles is \[{{180}^{o}}\].
Opposite phase means the phase difference between the particle is an odd multiple of \[\pi (say\,\,\pi ,\,\,3\pi ,\,\,5\pi ,\,\,7\pi .....)\] or the path difference is an odd multiple of \[\lambda (\text{say}\,\,\frac{\lambda }{2},\,\frac{3\lambda }{2}\,,......)\] or the time interval is an odd multiple of (T / 2).
(3) Phase difference : If two particles performs S.H.M and their equation are
\[{{y}_{1}}=a\sin (\omega \,t+{{\varphi }_{1}})\]and \[{{y}_{2}}=a\sin (\omega \,t+{{\varphi }_{2}})\] then phase difference \[\Delta \varphi =(\omega \,t+{{\varphi }_{2}})-(\omega \,t+{{\varphi }_{1}})\]\[={{\varphi }_{2}}-{{\varphi }_{1}}\]
(1) Simple harmonic motion is a special type of periodic motion, in which a particle moves to and fro repeatedly about a mean position.
(2) In linear S.H.M. a restoring force which is always directed towards the mean position and whose magnitude at any instant is directly proportional to the displacement of the particle from the mean position at that instant i.e. Restoring force \[\mu \] Displacement of the particle from mean position.
\[F\propto -x\Rightarrow F=-kx\]
Where k is known as force constant. Its S.I. unit is Newton/meter and dimension is \[[M{{T}^{-2}}]\].
(3) In stead of straight line motion, if particle or centre of mass of body is oscillating on a small arc of circular path, then for angular S.H.M.
Restoring torque \[(\tau )\propto -\]Angular displacement \[(\theta )\]
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |
