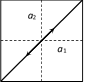
 \[\Rightarrow \]\[\frac{x}{{{a}_{1}}}=\frac{y}{{{a}_{2}}}\Rightarrow y=\frac{{{a}_{2}}}{{{a}_{1}}}x\]
This is a straight line passes through origin and it's slope is \[\frac{{{a}_{2}}}{{{a}_{1}}}\].
Lissajou's figures in other conditions (with \[\frac{{{\omega }_{1}}}{{{\omega }_{2}}}=1)\]
\[\Rightarrow \]\[\frac{x}{{{a}_{1}}}=\frac{y}{{{a}_{2}}}\Rightarrow y=\frac{{{a}_{2}}}{{{a}_{1}}}x\]
This is a straight line passes through origin and it's slope is \[\frac{{{a}_{2}}}{{{a}_{1}}}\].
Lissajou's figures in other conditions (with \[\frac{{{\omega }_{1}}}{{{\omega }_{2}}}=1)\]
| Phase diff. \[(\phi )\] | Equation | Figure | |||||
| \[\frac{\pi }{4}\] | \[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{\sqrt{2}xy}{{{a}_{1}}{{a}_{2}}}=\frac{1}{2}\] |
Oblique ellipse

|
|||||
| \[\frac{\pi }{2}\] | \[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}=1\] | 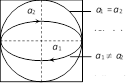 |
|||||
| \[\frac{3\pi }{4}\] | \[\frac{{{x}^{2}}}{a_{1}^{2}}+\frac{{{y}^{2}}}{a_{2}^{2}}-\frac{\sqrt{2}xy}{{{a}_{1}}{{a}_{2}}}=\frac{1}{2}\] |
Oblique ellipse

|
|||||
| \[\pi \] | more...
 (1) Free oscillation
(i) The oscillation of a particle with fundamental frequency under the influence of restoring force are defined as free oscillations
(ii) The amplitude, frequency and energy of oscillation remains constant
(iii) Frequency of free oscillation is called natural frequency because it depends upon the nature and structure of the body.
(1) Free oscillation
(i) The oscillation of a particle with fundamental frequency under the influence of restoring force are defined as free oscillations
(ii) The amplitude, frequency and energy of oscillation remains constant
(iii) Frequency of free oscillation is called natural frequency because it depends upon the nature and structure of the body.
 (2) Damped oscillation
(i) The oscillation of a body whose amplitude goes on decreasing with time are defined as damped oscillation
(ii) In these oscillation the amplitude of oscillation decreases exponentially due to damping forces like frictional force, viscous force, hystersis etc.
(iii) Due to decrease in amplitude the energy of the oscillator also goes on decreasing exponentially
(2) Damped oscillation
(i) The oscillation of a body whose amplitude goes on decreasing with time are defined as damped oscillation
(ii) In these oscillation the amplitude of oscillation decreases exponentially due to damping forces like frictional force, viscous force, hystersis etc.
(iii) Due to decrease in amplitude the energy of the oscillator also goes on decreasing exponentially
 (iv) The force produces a resistance to the oscillation is called damping force.
If the velocity of oscillator is v then
Damping force \[{{F}_{d}}=-\,bv,\] b = damping constant
(v) Resultant force on a damped oscillator is given by
\[F={{F}_{R}}+{{F}_{d}}=-Kx-Kv\]\[\Rightarrow \frac{m{{d}^{2}}x}{d{{t}^{2}}}+b\frac{dx}{dt}+Kx=0\]
(vi) Displacement of damped oscillator is given by
\[x={{x}_{m}}{{e}^{-bt/2m}}\sin ({\omega }'t+\varphi )\] where \[{\omega }'=\]angular frequency of the damped oscillator \[=\sqrt{\omega _{0}^{2}-{{(b/2m)}^{2}}}\]
The amplitude decreases continuously with time according to
\[x={{x}_{m}}{{e}^{-(b/2m)t}}\]
(vii) For a damped oscillator if the damping is small then the mechanical energy decreases exponentially with time as
\[E=\frac{1}{2}Kx_{m}^{2}{{e}^{-bt/m}}\]
(3) Forced oscillation
(i) The oscillation in which a body oscillates under the influence of an external periodic force are known as forced oscillation
(ii) The amplitude of oscillator decrease due to damping forces but on account of the energy gained from the external source it remains constant.
(iii) Resonance : When the frequency of external force is equal to the natural frequency of the oscillator. Then this state is known as the state of resonance. And this frequency is known as resonant frequency.
(iv) While swinging in a swing if you apply a push periodically by pressing your feet against the ground, you find that not only the oscillations can now be maintained but the amplitude can also be increased. Under this condition the swing has forced or driven oscillation.
(v) In forced oscillation, frequency of damped oscillator is equal to the frequency of external force.
(vi) Suppose an external driving force is represented by
\[F(t)={{F}_{0}}\cos {{\omega }_{d}}t\]
The motion of a particle under combined action of
(a) Restoring force \[(-Kx)\]
(b) Damping force \[(-bv)\]and
(c) Driving force \[F(t)\] is given by \[ma=-Kx-bv+{{F}_{0}}\cos {{\omega }_{d}}t\]
\[\Rightarrow \]\[{{m}^{2}}\frac{{{d}^{2}}x}{{{d}^{2}}}+Kx+b\frac{dx}{dt}={{F}_{0}}\cos {{\omega }_{d}}t\]
The solution of this equation gives \[x={{x}_{0}}\sin ({{\omega }_{d}}t+\varphi )\] with amplitude \[{{x}_{0}}=\frac{{{F}_{0}}/m}{\sqrt{({{\omega }^{2}}-\omega _{0}^{2})+{{(b\omega /m)}^{2}}}}\] and \[\tan \theta =\frac{({{\omega }^{2}}-\omega _{0}^{2})}{b\omega /m}\]
where \[{{\omega }_{0}}=\sqrt{\frac{K}{m}}=\] Natural frequency of oscillator.
(vii) Amplitude resonance : The amplitude of forced oscillator depends upon the frequency \[{{\omega }_{d}}\] of external force.
When \[\omega ={{\omega }_{d}},\] the amplitude is maximum but not infinite because of presence of damping force. The corresponds frequency is called resonant frequency \[({{\omega }_{0}})\].
(iv) The force produces a resistance to the oscillation is called damping force.
If the velocity of oscillator is v then
Damping force \[{{F}_{d}}=-\,bv,\] b = damping constant
(v) Resultant force on a damped oscillator is given by
\[F={{F}_{R}}+{{F}_{d}}=-Kx-Kv\]\[\Rightarrow \frac{m{{d}^{2}}x}{d{{t}^{2}}}+b\frac{dx}{dt}+Kx=0\]
(vi) Displacement of damped oscillator is given by
\[x={{x}_{m}}{{e}^{-bt/2m}}\sin ({\omega }'t+\varphi )\] where \[{\omega }'=\]angular frequency of the damped oscillator \[=\sqrt{\omega _{0}^{2}-{{(b/2m)}^{2}}}\]
The amplitude decreases continuously with time according to
\[x={{x}_{m}}{{e}^{-(b/2m)t}}\]
(vii) For a damped oscillator if the damping is small then the mechanical energy decreases exponentially with time as
\[E=\frac{1}{2}Kx_{m}^{2}{{e}^{-bt/m}}\]
(3) Forced oscillation
(i) The oscillation in which a body oscillates under the influence of an external periodic force are known as forced oscillation
(ii) The amplitude of oscillator decrease due to damping forces but on account of the energy gained from the external source it remains constant.
(iii) Resonance : When the frequency of external force is equal to the natural frequency of the oscillator. Then this state is known as the state of resonance. And this frequency is known as resonant frequency.
(iv) While swinging in a swing if you apply a push periodically by pressing your feet against the ground, you find that not only the oscillations can now be maintained but the amplitude can also be increased. Under this condition the swing has forced or driven oscillation.
(v) In forced oscillation, frequency of damped oscillator is equal to the frequency of external force.
(vi) Suppose an external driving force is represented by
\[F(t)={{F}_{0}}\cos {{\omega }_{d}}t\]
The motion of a particle under combined action of
(a) Restoring force \[(-Kx)\]
(b) Damping force \[(-bv)\]and
(c) Driving force \[F(t)\] is given by \[ma=-Kx-bv+{{F}_{0}}\cos {{\omega }_{d}}t\]
\[\Rightarrow \]\[{{m}^{2}}\frac{{{d}^{2}}x}{{{d}^{2}}}+Kx+b\frac{dx}{dt}={{F}_{0}}\cos {{\omega }_{d}}t\]
The solution of this equation gives \[x={{x}_{0}}\sin ({{\omega }_{d}}t+\varphi )\] with amplitude \[{{x}_{0}}=\frac{{{F}_{0}}/m}{\sqrt{({{\omega }^{2}}-\omega _{0}^{2})+{{(b\omega /m)}^{2}}}}\] and \[\tan \theta =\frac{({{\omega }^{2}}-\omega _{0}^{2})}{b\omega /m}\]
where \[{{\omega }_{0}}=\sqrt{\frac{K}{m}}=\] Natural frequency of oscillator.
(vii) Amplitude resonance : The amplitude of forced oscillator depends upon the frequency \[{{\omega }_{d}}\] of external force.
When \[\omega ={{\omega }_{d}},\] the amplitude is maximum but not infinite because of presence of damping force. The corresponds frequency is called resonant frequency \[({{\omega }_{0}})\].
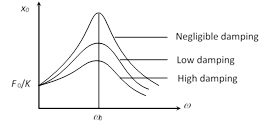 (viii) Energy more...
(viii) Energy more...
(1) S.H.M. of a liquid in U tube : If a liquid of density r contained in a vertical U tube performs S.H.M. in its two limbs. Then time period
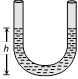 \[T=2\pi \sqrt{\frac{L}{2g}}\]\[=2\pi \sqrt{\frac{h}{g}}\]
where \[L=\] Total length of liquid column,
\[h=\] Height of undisturbed liquid in each limb \[(L-2h)\]
(2) S.H.M. of a floating cylinder : If \[l\] is the length of cylinder dipping in liquid then
\[T=2\pi \sqrt{\frac{L}{2g}}\]\[=2\pi \sqrt{\frac{h}{g}}\]
where \[L=\] Total length of liquid column,
\[h=\] Height of undisturbed liquid in each limb \[(L-2h)\]
(2) S.H.M. of a floating cylinder : If \[l\] is the length of cylinder dipping in liquid then
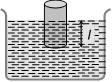 Time period \[T=2\pi \sqrt{\frac{l}{g}}\]
(3) S.H.M. of a small ball rolling down in hemi-spherical bowl
Time period \[T=2\pi \sqrt{\frac{l}{g}}\]
(3) S.H.M. of a small ball rolling down in hemi-spherical bowl
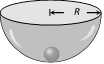 \[T=2\pi \sqrt{\frac{R-r}{g}}\]
\[R=\] Radius of the bowl
\[r=\]Radius of the ball
(4) S.H.M. of a piston in a cylinder
\[T=2\pi \sqrt{\frac{R-r}{g}}\]
\[R=\] Radius of the bowl
\[r=\]Radius of the ball
(4) S.H.M. of a piston in a cylinder
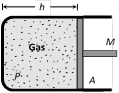 \[T=2\pi \sqrt{\frac{Mh}{PA}}\]
\[M=\] mass of the piston
\[A=\] area of cross section
\[h=\] height of cylinder
\[P=\] pressure in a cylinder
(5) S.H.M. of a body in a tunnel dug along any chord of earth
\[T=2\pi \sqrt{\frac{Mh}{PA}}\]
\[M=\] mass of the piston
\[A=\] area of cross section
\[h=\] height of cylinder
\[P=\] pressure in a cylinder
(5) S.H.M. of a body in a tunnel dug along any chord of earth
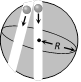 \[T=2\pi \sqrt{\frac{R}{g}}\]= 84.6 minutes
(6) Torsional pendulum : In a torsional pendulum an object is suspended from a wire. If such a wire is twisted, due to elasticity it exert a restoring toque \[\tau =C\theta \].
\[T=2\pi \sqrt{\frac{R}{g}}\]= 84.6 minutes
(6) Torsional pendulum : In a torsional pendulum an object is suspended from a wire. If such a wire is twisted, due to elasticity it exert a restoring toque \[\tau =C\theta \].
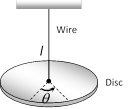 In this case time period is given by
\[T=2\pi \sqrt{\frac{I}{C}}\]
where \[l=\] Moment of inertia a disc
\[C=\] Torsional constant of wire \[=\frac{\pi \eta {{r}^{4}}}{2l}\]
\[\eta =\] Modulus of elasticity of wire and
\[r=\]Radius of wire
(7) Longitudinal oscillations of an elastic wire : Wire/string pulled a distance \[\Delta l\] and left. It executes longitudinal oscillations. Restoring force \[F=-\,AY\,\left( \frac{\Delta l}{l} \right)\]
In this case time period is given by
\[T=2\pi \sqrt{\frac{I}{C}}\]
where \[l=\] Moment of inertia a disc
\[C=\] Torsional constant of wire \[=\frac{\pi \eta {{r}^{4}}}{2l}\]
\[\eta =\] Modulus of elasticity of wire and
\[r=\]Radius of wire
(7) Longitudinal oscillations of an elastic wire : Wire/string pulled a distance \[\Delta l\] and left. It executes longitudinal oscillations. Restoring force \[F=-\,AY\,\left( \frac{\Delta l}{l} \right)\]
 \[Y=\]Young's modulus
\[A=\] Area of cross-section
Hence \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{ml}{AY}}\]
\[Y=\]Young's modulus
\[A=\] Area of cross-section
Hence \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{ml}{AY}}\]
(1) Series combination : If two springs of spring constants \[{{K}_{1}}\] and \[{{K}_{2}}\] are joined in series as shown then
 (i) In series combination equal forces acts on spring but extension in springs are different.
(ii) Spring constants of combination
\[\frac{1}{{{k}_{s}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\]\[\Rightarrow \]\[{{k}_{s}}=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}\]
(iii) If n springs of different force constant are connected in series having force constant \[{{k}_{1}},{{k}_{2}},{{k}_{3}}.......\] respectively then
\[\frac{1}{{{k}_{S}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}+\frac{1}{{{k}_{3}}}+........\]
If all spring have same spring constant then \[{{k}_{S}}=\frac{k}{n}\]
(iv) Time period of combination \[T=2\pi \sqrt{\frac{m}{{{k}_{S}}}}=2\pi \sqrt{\frac{m({{k}_{1}}+{{k}_{2}})}{{{k}_{1}}{{k}_{2}}}}\]
(2) Parallel combination : If the springs are connected in parallel as shown
(i) In series combination equal forces acts on spring but extension in springs are different.
(ii) Spring constants of combination
\[\frac{1}{{{k}_{s}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}\]\[\Rightarrow \]\[{{k}_{s}}=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}\]
(iii) If n springs of different force constant are connected in series having force constant \[{{k}_{1}},{{k}_{2}},{{k}_{3}}.......\] respectively then
\[\frac{1}{{{k}_{S}}}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}+\frac{1}{{{k}_{3}}}+........\]
If all spring have same spring constant then \[{{k}_{S}}=\frac{k}{n}\]
(iv) Time period of combination \[T=2\pi \sqrt{\frac{m}{{{k}_{S}}}}=2\pi \sqrt{\frac{m({{k}_{1}}+{{k}_{2}})}{{{k}_{1}}{{k}_{2}}}}\]
(2) Parallel combination : If the springs are connected in parallel as shown
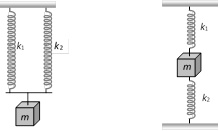
 (i) In parallel combination different forces acts on different springs but extension in springs are same
(ii) Spring constants of combination \[{{k}_{P}}={{k}_{1}}+{{k}_{2}}\]
(iii) If n springs of different force constant are connected in parallel having force constant \[{{k}_{1}},{{k}_{2}},{{k}_{3}}.......\] respectively then \[{{k}_{P}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}}+...\]
If all spring have same spring constant then \[{{k}_{P}}=nk\]
(iv) Time period of combination \[{{T}_{P}}=2\pi \sqrt{\frac{m}{{{k}_{P}}}}=2\pi \sqrt{\frac{m}{({{k}_{1}}+{{k}_{2}})}}\]
(i) In parallel combination different forces acts on different springs but extension in springs are same
(ii) Spring constants of combination \[{{k}_{P}}={{k}_{1}}+{{k}_{2}}\]
(iii) If n springs of different force constant are connected in parallel having force constant \[{{k}_{1}},{{k}_{2}},{{k}_{3}}.......\] respectively then \[{{k}_{P}}={{k}_{1}}+{{k}_{2}}+{{k}_{3}}+...\]
If all spring have same spring constant then \[{{k}_{P}}=nk\]
(iv) Time period of combination \[{{T}_{P}}=2\pi \sqrt{\frac{m}{{{k}_{P}}}}=2\pi \sqrt{\frac{m}{({{k}_{1}}+{{k}_{2}})}}\]
A point mass suspended from a mass less spring or placed on a frictionless horizontal plane attached with spring (fig.) constitutes a linear harmonic spring pendulum
 Time period \[T=2\pi \sqrt{\frac{\text{Inertia}\,\text{factor}}{\text{Spring}\,\text{factor}}}\]\[=2\pi \sqrt{\frac{m}{k}}\]
and Frequency \[n=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\]
(1) Time period of a spring pendulum depends on the mass suspended \[\Rightarrow T\propto \sqrt{m}\] or \[n\propto \frac{1}{\sqrt{m}}\]i.e. greater the mass greater will be the inertia and so lesser will be the frequency of oscillation and greater will be the time period.
(2) The time period depends on the force constant k of the spring i.e. \[T\propto \frac{1}{\sqrt{k}}\] or \[n\propto \sqrt{k}\,\,\]
(3) Time of a spring pendulum is independent of acceleration due to gravity. That is why a clock based on spring pendulum will keep proper time every where on a hill or moon or in a satellite and time period of a spring pendulum will not change inside a liquid if damping effects are neglected.
(4) Massive spring : If the spring has a mass M and mass m is suspended from it, effective mass is given by \[{{m}_{eff}}=m+\frac{M}{3}\]. Hence \[T=2\pi \sqrt{\frac{{{m}_{eff}}}{k}}\]
(5) Reduced mass : If two masses of mass \[{{m}_{1}}\] and \[{{m}_{2}}\] are connected by a spring and made to oscillate on horizontal surface, the reduced mass \[{{m}_{r}}\] is given by \[v=a\omega \sqrt{1-{{\sin }^{2}}\omega \,t}\] so that \[\left| \,\sin \,\omega \,t\, \right|=\text{maximum}=1\]
Time period \[T=2\pi \sqrt{\frac{\text{Inertia}\,\text{factor}}{\text{Spring}\,\text{factor}}}\]\[=2\pi \sqrt{\frac{m}{k}}\]
and Frequency \[n=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\]
(1) Time period of a spring pendulum depends on the mass suspended \[\Rightarrow T\propto \sqrt{m}\] or \[n\propto \frac{1}{\sqrt{m}}\]i.e. greater the mass greater will be the inertia and so lesser will be the frequency of oscillation and greater will be the time period.
(2) The time period depends on the force constant k of the spring i.e. \[T\propto \frac{1}{\sqrt{k}}\] or \[n\propto \sqrt{k}\,\,\]
(3) Time of a spring pendulum is independent of acceleration due to gravity. That is why a clock based on spring pendulum will keep proper time every where on a hill or moon or in a satellite and time period of a spring pendulum will not change inside a liquid if damping effects are neglected.
(4) Massive spring : If the spring has a mass M and mass m is suspended from it, effective mass is given by \[{{m}_{eff}}=m+\frac{M}{3}\]. Hence \[T=2\pi \sqrt{\frac{{{m}_{eff}}}{k}}\]
(5) Reduced mass : If two masses of mass \[{{m}_{1}}\] and \[{{m}_{2}}\] are connected by a spring and made to oscillate on horizontal surface, the reduced mass \[{{m}_{r}}\] is given by \[v=a\omega \sqrt{1-{{\sin }^{2}}\omega \,t}\] so that \[\left| \,\sin \,\omega \,t\, \right|=\text{maximum}=1\]
 (6) If a spring pendulum, oscillating in a vertical plane is made to oscillate on a horizontal surface, (or on inclined plane) time period will remain unchanged.
(7) Equilibrium position for a spring in a horizontal plain is the position of natural length of spring as weight is balanced by reaction. While in case of vertical motion equilibrium position will be \[l+{{y}_{0}}\] with \[k{{y}_{0}}=mg\]
(6) If a spring pendulum, oscillating in a vertical plane is made to oscillate on a horizontal surface, (or on inclined plane) time period will remain unchanged.
(7) Equilibrium position for a spring in a horizontal plain is the position of natural length of spring as weight is balanced by reaction. While in case of vertical motion equilibrium position will be \[l+{{y}_{0}}\] with \[k{{y}_{0}}=mg\]
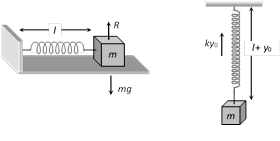 If the stretch in a vertically loaded spring is \[{{y}_{0}}\] then for equilibrium of mass m, \[k{{y}_{0}}=mg\] i.e. \[\frac{m}{k}=\frac{{{y}_{0}}}{g}\]
So that \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{{{y}_{0}}}{g}}\]
Time period does not depends on ?g? because along with g, \[{{y}_{o}}\] will also change in such a way that \[\frac{{{y}_{0}}}{g}=\frac{m}{k}\] remains constant
If the stretch in a vertically loaded spring is \[{{y}_{0}}\] then for equilibrium of mass m, \[k{{y}_{0}}=mg\] i.e. \[\frac{m}{k}=\frac{{{y}_{0}}}{g}\]
So that \[T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{{{y}_{0}}}{g}}\]
Time period does not depends on ?g? because along with g, \[{{y}_{o}}\] will also change in such a way that \[\frac{{{y}_{0}}}{g}=\frac{m}{k}\] remains constant
When a spring is stretched or compressed from its normal position \[(x=0)\] by a small distance \[x,\] then a restoring force is produced in the spring because it obeys Hook's law
i.e. \[F\propto -x\]\[\Rightarrow \]\[F=-\,k\,x\]
where k is called spring constant.
(i) It's S.I. unit Newton/metre, C.G.S unit Dyne/cm and dimension is \[[M{{T}^{-2}}]\]
(ii) Actually k is a measure of the stiffness/softness of the spring.
(iii) For massless spring constant restoring elastic force is same every where
(iv) When a spring compressed or stretched then work done is stored in the form of elastic potential energy in it.
(v) Spring constant depend upon radius and length of the wire used in spring.
(vi) The spring constant k is inversely proportional to the spring length.
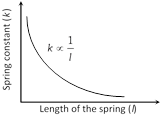 \[k\propto \frac{1}{\text{Extension}}\propto \frac{1}{\text{Length}\,\text{of spring}}\]
That means if the length of spring is halved then its force constant becomes double.
(vii) When a spring of length \[l\] is cut in two pieces of length \[{{l}_{1}}\] and \[{{l}_{2}}\] such that \[{{l}_{1}}=n{{l}_{2}}\].
If the constant of a spring is k then spring constant of first part
\[{{k}_{1}}=\frac{k(n+1)}{n}\]
Spring constant of second part \[{{k}_{2}}=(n+1)k\]
and ratio of spring constant \[\frac{{{k}_{1}}}{{{k}_{2}}}=\frac{1}{n}\]
\[k\propto \frac{1}{\text{Extension}}\propto \frac{1}{\text{Length}\,\text{of spring}}\]
That means if the length of spring is halved then its force constant becomes double.
(vii) When a spring of length \[l\] is cut in two pieces of length \[{{l}_{1}}\] and \[{{l}_{2}}\] such that \[{{l}_{1}}=n{{l}_{2}}\].
If the constant of a spring is k then spring constant of first part
\[{{k}_{1}}=\frac{k(n+1)}{n}\]
Spring constant of second part \[{{k}_{2}}=(n+1)k\]
and ratio of spring constant \[\frac{{{k}_{1}}}{{{k}_{2}}}=\frac{1}{n}\]
(1) Infinite length pendulum : If the length of the pendulum is comparable to the radius of earth then
\[T=2\pi \sqrt{\frac{1}{g\left[ \frac{1}{l}+\frac{1}{R} \right]}}\]
(i) If \[l<<R\], then \[\frac{1}{l}>>\frac{1}{R}\] so \[T=2\pi \sqrt{\frac{l}{g}}\]
(ii) If \[l>>R(\to \infty )\,\text{then }\frac{1}{l}<\frac{1}{R}\] so \[T=2\pi \sqrt{\frac{R}{g}}=2\pi \sqrt{\frac{6.4\times {{10}^{6}}}{10}}\cong 84.6\] minutes
and it is the maximum time period which an oscillating simple pendulum can have
(iii) If \[l=R\] so \[T=2\pi \sqrt{\frac{R}{2g}}\cong 1hour\]
(2) Second's Pendulum : It is that simple pendulum whose time period of vibrations is two seconds.
Putting \[T=2\,\sec \] and \[g=9.8m/{{\sec }^{2}}\] in \[T=2\pi \sqrt{\frac{l}{g}}\] we get \[l=\frac{4\times 9.8}{4{{\pi }^{2}}}=0.993\]\[m=99.3\,m\]
Hence length of second?s pendulum is 99.3 cm or nearly 1 meter on earth surface.
For the moon the length of the second?s pendulum will be 1/6 meter [As \[{{g}_{moon}}=\frac{{{g}_{\text{Earth}}}}{6}\]]
(3) Compound pendulum : Any rigid body suspended from a fixed support constitutes a physical pendulum. Consider the situation when the body is displaced through a small angle \[\theta \]. Torque on the body about O is given by
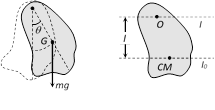 \[\tau =mgl\ \sin \theta \] ...(i)
where \[l=\] distance between point of suspension and centre of mass of the body.
If \[l\] be the M.I. of the body about O. Then \[\tau =I\alpha \] ...(ii)
From (i) and (ii), we get \[I\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-mgl\sin \theta \] as \[\theta \] and \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}\] are oppositely directed \[\Rightarrow \] \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-\frac{mgl}{I}\theta \] since \[\theta \]is very small
Comparing with the equation \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-{{\omega }^{2}}\theta .\]we get
\[\omega =\sqrt{\frac{mgl}{I}}
\Rightarrow T=2\pi \sqrt{\frac{I}{mgl}}\]
Also \[I={{I}_{cm}}+m{{l}^{2}}\] (Parallel axis theorem)
\[=m{{k}^{2}}+m{{l}^{2}}\] (where \[k=\] radius of gyration)
\[\therefore \] \[T=2\pi \sqrt{\frac{m{{K}^{2}}+m{{l}^{2}}}{mgl}}=2\pi \sqrt{\frac{\frac{{{K}^{2}}}{l}+l}{g}}\]\[=2\pi \sqrt{\frac{{{l}_{\text{eff}}}}{g}}\]
\[{{l}_{eff}}=\] Effective length of pendulum = Distance between point of suspension and centre of mass.
Some common physical pendulum
\[\tau =mgl\ \sin \theta \] ...(i)
where \[l=\] distance between point of suspension and centre of mass of the body.
If \[l\] be the M.I. of the body about O. Then \[\tau =I\alpha \] ...(ii)
From (i) and (ii), we get \[I\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-mgl\sin \theta \] as \[\theta \] and \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}\] are oppositely directed \[\Rightarrow \] \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-\frac{mgl}{I}\theta \] since \[\theta \]is very small
Comparing with the equation \[\frac{{{d}^{2}}\theta }{d{{t}^{2}}}=-{{\omega }^{2}}\theta .\]we get
\[\omega =\sqrt{\frac{mgl}{I}}
\Rightarrow T=2\pi \sqrt{\frac{I}{mgl}}\]
Also \[I={{I}_{cm}}+m{{l}^{2}}\] (Parallel axis theorem)
\[=m{{k}^{2}}+m{{l}^{2}}\] (where \[k=\] radius of gyration)
\[\therefore \] \[T=2\pi \sqrt{\frac{m{{K}^{2}}+m{{l}^{2}}}{mgl}}=2\pi \sqrt{\frac{\frac{{{K}^{2}}}{l}+l}{g}}\]\[=2\pi \sqrt{\frac{{{l}_{\text{eff}}}}{g}}\]
\[{{l}_{eff}}=\] Effective length of pendulum = Distance between point of suspension and centre of mass.
Some common physical pendulum
|