 (1) Electric field intensity \[(\vec{E})\]: The electric field intensity at any point is defined as the force experienced by a unit positive charge placed at that point. \[\vec{E}= \frac{{\vec{F}}}{{{q}_{0}}}\]
Where \[{{q}_{0}}\to 0\] so that presence of this charge may not affect the source charge Q and its electric field is not changed, therefore expression for electric field intensity can be better written as \[\vec{E}=\underset{{{q}_{0}}\to 0}{\mathop{\text{Lim}}}\,\,\,\,\frac{{\vec{F}}}{{{q}_{\mathbf{0}}}}\]
(2) Unit and Dimensional formula
It's S.I. unit \[\frac{Newton}{coulomb}=\frac{volt}{meter}=\frac{Joule}{coulomb\times meter}\]
and C.G.S. unit - dyne/stat coulomb.
Dimension :\[[E]=[ML{{T}^{-3}}{{A}^{-1}}]\]
(3) Direction of electric field : Electric field (intensity) \[\vec{E}\] is a vector quantity. Electric field due to a positive charge is always away from the charge and that due to a negative charge is always towards the charge.
(4) Relation between electric force and electric field : In an electric field \[\vec{E}\] a charge (Q) experiences a force \[\overrightarrow{F}=Q\overrightarrow{E}\]. If charge is positive then force is directed in the direction of field while if charge is negative force acts on it in the opposite direction of field
(1) Electric field intensity \[(\vec{E})\]: The electric field intensity at any point is defined as the force experienced by a unit positive charge placed at that point. \[\vec{E}= \frac{{\vec{F}}}{{{q}_{0}}}\]
Where \[{{q}_{0}}\to 0\] so that presence of this charge may not affect the source charge Q and its electric field is not changed, therefore expression for electric field intensity can be better written as \[\vec{E}=\underset{{{q}_{0}}\to 0}{\mathop{\text{Lim}}}\,\,\,\,\frac{{\vec{F}}}{{{q}_{\mathbf{0}}}}\]
(2) Unit and Dimensional formula
It's S.I. unit \[\frac{Newton}{coulomb}=\frac{volt}{meter}=\frac{Joule}{coulomb\times meter}\]
and C.G.S. unit - dyne/stat coulomb.
Dimension :\[[E]=[ML{{T}^{-3}}{{A}^{-1}}]\]
(3) Direction of electric field : Electric field (intensity) \[\vec{E}\] is a vector quantity. Electric field due to a positive charge is always away from the charge and that due to a negative charge is always towards the charge.
(4) Relation between electric force and electric field : In an electric field \[\vec{E}\] a charge (Q) experiences a force \[\overrightarrow{F}=Q\overrightarrow{E}\]. If charge is positive then force is directed in the direction of field while if charge is negative force acts on it in the opposite direction of field
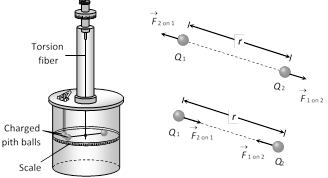 \[F\propto \frac{Q{}_{1}Q{}_{{{2}_{{}}}}}{{{r}^{2}}}\] i.e., \[F=\frac{kQ{}_{1}Q{}_{2}}{{{r}^{2}}}\](k = Proportionality constant)
In C.G.S. (for air ) \[k=1,\] \[F=\frac{{{Q}_{1}}\,{{Q}_{2}}}{{{r}^{2}}}\] Dyne
In S.I. (for air) \[k=\frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}\frac{N\text{-}m{}^{2}}{C{}^{2}}\]
\[\Rightarrow \] \[F=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}\] Newton (1 Newton \[={{10}^{5}}\] Dyne)
\[{{\varepsilon }_{0}}=\]Absolute permittivity of air or free space
\[=8.85\times {{10}^{-12}}\frac{{{C}^{2}}}{N-{{m}^{2}}}\]\[\left( =\frac{Farad}{m} \right)\]. It's Dimensional formula is \[[{{M}^{-1}}{{L}^{-3}}{{T}^{4}}{{A}^{2}}]\]
(1) Vector form of coulomb's law : Vector form of Coulomb's law is \[{{\overrightarrow{F\,}}_{12}}=K.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{3}}}{{\overrightarrow{\,r}}_{12}}=K.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}{{\hat{r}}_{12}},\] where \[{{\hat{r}}_{12}}\] is the unit vector from first charge to second charge along the line joining the two charges.
(2) Effect of medium : When a dielectric medium is completely filled in between charges rearrangement of the charges inside the dielectric medium takes place and the force between the same two charges decreases by a factor of K (dielectric constant)
\[F\propto \frac{Q{}_{1}Q{}_{{{2}_{{}}}}}{{{r}^{2}}}\] i.e., \[F=\frac{kQ{}_{1}Q{}_{2}}{{{r}^{2}}}\](k = Proportionality constant)
In C.G.S. (for air ) \[k=1,\] \[F=\frac{{{Q}_{1}}\,{{Q}_{2}}}{{{r}^{2}}}\] Dyne
In S.I. (for air) \[k=\frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}\frac{N\text{-}m{}^{2}}{C{}^{2}}\]
\[\Rightarrow \] \[F=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}\] Newton (1 Newton \[={{10}^{5}}\] Dyne)
\[{{\varepsilon }_{0}}=\]Absolute permittivity of air or free space
\[=8.85\times {{10}^{-12}}\frac{{{C}^{2}}}{N-{{m}^{2}}}\]\[\left( =\frac{Farad}{m} \right)\]. It's Dimensional formula is \[[{{M}^{-1}}{{L}^{-3}}{{T}^{4}}{{A}^{2}}]\]
(1) Vector form of coulomb's law : Vector form of Coulomb's law is \[{{\overrightarrow{F\,}}_{12}}=K.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{3}}}{{\overrightarrow{\,r}}_{12}}=K.\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}{{\hat{r}}_{12}},\] where \[{{\hat{r}}_{12}}\] is the unit vector from first charge to second charge along the line joining the two charges.
(2) Effect of medium : When a dielectric medium is completely filled in between charges rearrangement of the charges inside the dielectric medium takes place and the force between the same two charges decreases by a factor of K (dielectric constant)
 i.e. \[{{F}_{medium}}=\frac{{{F}_{air}}}{K}\]\[=\frac{1}{4\pi {{\varepsilon }_{0}}K}.\,\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}\]
(Here \[{{\varepsilon }_{0}}K={{\varepsilon }_{0}}\,{{\varepsilon }_{r}}=\varepsilon \] = permittivity of medium)
If a dielectric medium (dielectric constant K, thickness t) is partially filled between the charges then effective air separation between the charges becomes \[(r-t\,+t\sqrt{K})\]
i.e. \[{{F}_{medium}}=\frac{{{F}_{air}}}{K}\]\[=\frac{1}{4\pi {{\varepsilon }_{0}}K}.\,\frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}\]
(Here \[{{\varepsilon }_{0}}K={{\varepsilon }_{0}}\,{{\varepsilon }_{r}}=\varepsilon \] = permittivity of medium)
If a dielectric medium (dielectric constant K, thickness t) is partially filled between the charges then effective air separation between the charges becomes \[(r-t\,+t\sqrt{K})\]
 Hence force \[F=\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{{{Q}_{1}}{{Q}_{2}}}{{{(r-t+t\sqrt{K})}^{2}}}\]
(3) Principle of superposition : According to the principle of super position, total force acting on a given charge due to number of charges is the vector sum of the individual forces acting on that charge due to all the charges.
Hence force \[F=\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{{{Q}_{1}}{{Q}_{2}}}{{{(r-t+t\sqrt{K})}^{2}}}\]
(3) Principle of superposition : According to the principle of super position, total force acting on a given charge due to number of charges is the vector sum of the individual forces acting on that charge due to all the charges.
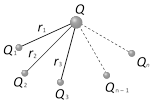 Consider number of charge \[{{Q}_{1}}\],\[{{Q}_{2}}\],\[{{Q}_{3}}\] ... are applying force on a charge Q.
Net force on Q will be
\[{{\overrightarrow{F}}_{net}}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+....+{{\overrightarrow{F}}_{n-1}}+{{\overrightarrow{F}}_{n}}\]
The magnitude of the resultant of two electric forces is given by
Consider number of charge \[{{Q}_{1}}\],\[{{Q}_{2}}\],\[{{Q}_{3}}\] ... are applying force on a charge Q.
Net force on Q will be
\[{{\overrightarrow{F}}_{net}}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+....+{{\overrightarrow{F}}_{n-1}}+{{\overrightarrow{F}}_{n}}\]
The magnitude of the resultant of two electric forces is given by
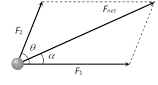 \[{{F}_{net}}=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \theta }\]
and \[\tan \alpha =\frac{{{F}_{2}}\sin \theta }{{{F}_{1}}+{{F}_{2}}\cos \theta }\]
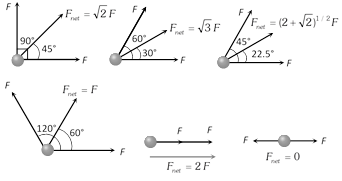
For problem solving remember following standard results.
\[{{F}_{net}}=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \theta }\]
and \[\tan \alpha =\frac{{{F}_{2}}\sin \theta }{{{F}_{1}}+{{F}_{2}}\cos \theta }\]
For problem solving remember following standard results.
 Fundamental forces of nature
Fundamental forces of nature
| Force | Nature and formula | Range | Relative strength | |||||||||||||||||
| Force of gravitation between two masses | more...
It is a simple apparatus with which the presence of electric charge on a body is detected (see figure). When metal knob is touched with a charged body, some charge is transferred to the gold leaves, which then diverges due to repulsion. The separation gives a rough idea of the amount of charge on the body. When a charged body brought near a charged electroscope, the leaves will further diverge, if the charge on body is similar to that on electroscope and will usually converge if opposite. If the induction effect is strong enough leaves after converging may again diverge.

A body can be charged by following methods.
(1) By friction : By rubbing two bodies together, both positive and negative charges in equal amounts appear simultaneously due to transfer of electrons from one body to the other.
(i) When a glass rod is rubbed with silk, the rod becomes positively charged while the silk becomes negatively charged. The decrease in the mass of glass rod is equal to the total mass of electrons lost by it.
(ii) Ebonite on rubbing with wool becomes negatively charged making the wool positively charged.
(iii) Clouds also get charged by friction. (iv) A comb moving through dry hair gets electrically charged. It starts attracting small bits of paper.
(v) During landing or take-off, the tyres of an aircraft get electrified therefore special material is used to manufacture them.
 (2) By electrostatic induction : If a charged body is brought near an uncharged body, one side of neutral body (closer to charged body) becomes oppositely charged while the other side becomes similarly charged.
(2) By electrostatic induction : If a charged body is brought near an uncharged body, one side of neutral body (closer to charged body) becomes oppositely charged while the other side becomes similarly charged.
 Induced charge can be lesser or equal to inducing charge (but never greater) and its maximum value is given by \[Q'=-Q\left[ 1-\frac{1}{K} \right]\] where Q is the inducing charge and K is the dielectric constant of the material of the uncharged body. It is also known as specific inductive capacity (SIC) of the medium, or relative permittivity er of the medium (relative means with respect to free space)
Different dielectric constants
Induced charge can be lesser or equal to inducing charge (but never greater) and its maximum value is given by \[Q'=-Q\left[ 1-\frac{1}{K} \right]\] where Q is the inducing charge and K is the dielectric constant of the material of the uncharged body. It is also known as specific inductive capacity (SIC) of the medium, or relative permittivity er of the medium (relative means with respect to free space)
Different dielectric constants
|