 Apparent frequency \[n'=n\,\left[ \frac{v-0}{v-(+{{v}_{S}})} \right]=n\,\left( \frac{v}{v-{{v}_{S}}} \right)\]
Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(2) Source is moving away from the observer.
Apparent frequency \[n'=n\,\left[ \frac{v-0}{v-(+{{v}_{S}})} \right]=n\,\left( \frac{v}{v-{{v}_{S}}} \right)\]
Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(2) Source is moving away from the observer.
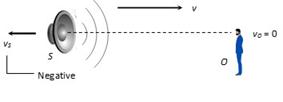 Apparent frequency \[n'=n\,\left[ \frac{v-0}{v-(-{{v}_{S}})} \right]=n\,\left( \frac{v}{v+{{v}_{S}}} \right)\]
Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\]
Case 2: Source is at rest but observer is moving.
(1) Observer is moving towards the source.
Apparent frequency \[n'=n\,\left[ \frac{v-0}{v-(-{{v}_{S}})} \right]=n\,\left( \frac{v}{v+{{v}_{S}}} \right)\]
Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\]
Case 2: Source is at rest but observer is moving.
(1) Observer is moving towards the source.
 Apparent frequency \[n'=n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v} \right]\]
Apparent wavelength \[\lambda '=\frac{(v+{{v}_{O}})}{n'}=\frac{(v+{{v}_{O}})}{n\frac{(v+{{v}_{O}})}{v}}=\frac{v}{n}=\lambda \]
(2) Observer is moving away from the source
Apparent frequency \[n'=n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v} \right]\]
Apparent wavelength \[\lambda '=\frac{(v+{{v}_{O}})}{n'}=\frac{(v+{{v}_{O}})}{n\frac{(v+{{v}_{O}})}{v}}=\frac{v}{n}=\lambda \]
(2) Observer is moving away from the source
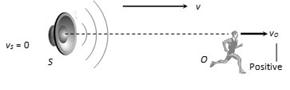 Apparent frequency \[n'=n\,\left[ \frac{v-(+{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v} \right]\]
Apparent wavelength \[\lambda '=\lambda \]
Case 3: When source and observer both are moving
(1) When both are moving towards each other
Apparent frequency \[n'=n\,\left[ \frac{v-(+{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v} \right]\]
Apparent wavelength \[\lambda '=\lambda \]
Case 3: When source and observer both are moving
(1) When both are moving towards each other
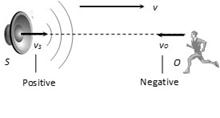 (i) Apparent frequency \[n'=n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-\,(+{{v}_{S}})} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v-{{v}_{S}}} \right]\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(iii) Velocity of wave with respect to observer \[=(v+{{v}_{O}})\]
(2) When both are moving away from each other.
(i) Apparent frequency \[n'=n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-\,(+{{v}_{S}})} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v-{{v}_{S}}} \right]\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(iii) Velocity of wave with respect to observer \[=(v+{{v}_{O}})\]
(2) When both are moving away from each other.
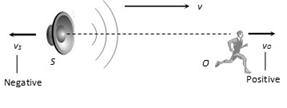 (i) Apparent frequency \[n'=n\,\left[ \frac{v-\,(+\,{{v}_{O}})}{v-\,(-\,{{v}_{S}})} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v+{{v}_{S}}} \right]\]
\[(n'<n)\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\] \[(\lambda '>\lambda )\]
Velocity of waves with respect to observer \[=(v{{v}_{O}})\]
(3) When source is moving behind observer
(i) Apparent frequency \[n'=n\,\left[ \frac{v-\,(+\,{{v}_{O}})}{v-\,(-\,{{v}_{S}})} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v+{{v}_{S}}} \right]\]
\[(n'<n)\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\] \[(\lambda '>\lambda )\]
Velocity of waves with respect to observer \[=(v{{v}_{O}})\]
(3) When source is moving behind observer
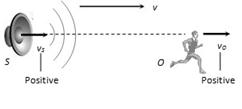 (i) Apparent frequency \[n'=n\,\left( \frac{v-{{v}_{O}}}{v-{{v}_{S}}} \right)\]
(a) If \[{{v}_{O}}<{{v}_{S}},\] then \[n'>n\]
(b) If \[{{v}_{O}}>{{v}_{S}}\] then \[n'<n\]
(c) If \[{{v}_{O}}={{v}_{S}}\] then \[n'<n\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(iii) Velocity of waves with respect to observer = \[(v-{{v}_{O}})\]
(4) When observer is moving behind the source
(i) Apparent frequency \[n'=n\,\left( \frac{v-{{v}_{O}}}{v-{{v}_{S}}} \right)\]
(a) If \[{{v}_{O}}<{{v}_{S}},\] then \[n'>n\]
(b) If \[{{v}_{O}}>{{v}_{S}}\] then \[n'<n\]
(c) If \[{{v}_{O}}={{v}_{S}}\] then \[n'<n\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v-{{v}_{S}}}{v} \right)\]
(iii) Velocity of waves with respect to observer = \[(v-{{v}_{O}})\]
(4) When observer is moving behind the source
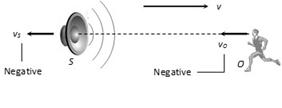 (i) Apparent frequency \[n'=n\,\left( \frac{v-\,(-{{v}_{O}})}{v-(-{{v}_{S}})} \right)\]
(a) If \[{{v}_{O}}>{{v}_{S}},\] then \[n'>n\]
(b) If \[{{v}_{O}}<{{v}_{S}}\] then \[n'<n\]
(c) If \[{{v}_{O}}={{v}_{S}}\] then \[n'<n\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\]
(iii) The velocity of waves with respect to observer = \[(v-{{v}_{O}})\]
Case 4: Crossing (1) Moving sound source crosses a stationary observer
(i) Apparent frequency \[n'=n\,\left( \frac{v-\,(-{{v}_{O}})}{v-(-{{v}_{S}})} \right)\]
(a) If \[{{v}_{O}}>{{v}_{S}},\] then \[n'>n\]
(b) If \[{{v}_{O}}<{{v}_{S}}\] then \[n'<n\]
(c) If \[{{v}_{O}}={{v}_{S}}\] then \[n'<n\]
(ii) Apparent wavelength \[\lambda '=\lambda \,\left( \frac{v+{{v}_{S}}}{v} \right)\]
(iii) The velocity of waves with respect to observer = \[(v-{{v}_{O}})\]
Case 4: Crossing (1) Moving sound source crosses a stationary observer
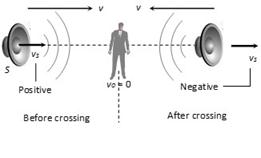 Apparent frequency before crossing
\[n{{'}_{Before}}=\,n\,\left[ \frac{v-0}{v-\,(+{{v}_{S}})} \right]=n\,\left[ \frac{v}{v-{{v}_{S}}} \right]\]
Apparent frequency
\[n{{'}_{After}}=\,n\,\left[ \frac{v-0}{v-\,(-{{v}_{S}})} \right]=n\,\left[ \frac{v}{v+{{v}_{S}}} \right]\]
Ratio of two frequency \[\frac{n{{'}_{Before}}}{n{{'}_{After}}}=\,\left[ \frac{v+{{v}_{S}}}{v-{{v}_{S}}} \right]>1\]
Change in apparent frequency \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{S}}v}{({{v}^{2}}-v_{S}^{2})}\]
If \[{{v}_{S}}<<v\] then \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{S}}}{v}\]
(2) Moving observer crosses a stationary source
Apparent frequency before crossing
\[n{{'}_{Before}}=\,n\,\left[ \frac{v-0}{v-\,(+{{v}_{S}})} \right]=n\,\left[ \frac{v}{v-{{v}_{S}}} \right]\]
Apparent frequency
\[n{{'}_{After}}=\,n\,\left[ \frac{v-0}{v-\,(-{{v}_{S}})} \right]=n\,\left[ \frac{v}{v+{{v}_{S}}} \right]\]
Ratio of two frequency \[\frac{n{{'}_{Before}}}{n{{'}_{After}}}=\,\left[ \frac{v+{{v}_{S}}}{v-{{v}_{S}}} \right]>1\]
Change in apparent frequency \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{S}}v}{({{v}^{2}}-v_{S}^{2})}\]
If \[{{v}_{S}}<<v\] then \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{S}}}{v}\]
(2) Moving observer crosses a stationary source
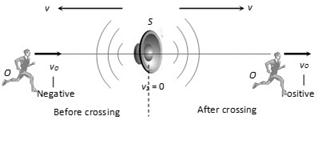 Apparent frequency before crossing
\[n{{'}_{Before}}=\,n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v} \right]\]
Apparent frequency
\[n{{'}_{After}}=\,n\,\left[ \frac{v-(+{{v}_{O}})}{v-\,0} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v} \right]\]
Ratio of two frequency \[\frac{n{{'}_{Before}}}{n{{'}_{After}}}=\,\left[ \frac{v+{{v}_{S}}}{v-{{v}_{S}}} \right]\]
Change in apparent frequency \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{O}}}{v}\]
Case 5: Both moves in the same direction with same velocity \[n'=n,\], i.e. there will be no Doppler effect because relative motion between source and listener is zero.
Case 6: Source and listener moves at right angle to the direction of wave propagation. \[n'=n\]
It means there is no change in frequency of sound heard if there is a small displacement of more...
Apparent frequency before crossing
\[n{{'}_{Before}}=\,n\,\left[ \frac{v-\,(-\,{{v}_{O}})}{v-0} \right]=n\,\left[ \frac{v+{{v}_{O}}}{v} \right]\]
Apparent frequency
\[n{{'}_{After}}=\,n\,\left[ \frac{v-(+{{v}_{O}})}{v-\,0} \right]=n\,\left[ \frac{v-{{v}_{O}}}{v} \right]\]
Ratio of two frequency \[\frac{n{{'}_{Before}}}{n{{'}_{After}}}=\,\left[ \frac{v+{{v}_{S}}}{v-{{v}_{S}}} \right]\]
Change in apparent frequency \[n{{'}_{Before}}-n{{'}_{After}}=\frac{2n{{v}_{O}}}{v}\]
Case 5: Both moves in the same direction with same velocity \[n'=n,\], i.e. there will be no Doppler effect because relative motion between source and listener is zero.
Case 6: Source and listener moves at right angle to the direction of wave propagation. \[n'=n\]
It means there is no change in frequency of sound heard if there is a small displacement of more...  Whenever there is a relative motion between a source of sound and the observer (listener), the frequency of sound heard by the observer is different from the actual frequency of sound emitted by the source.
The frequency observed by the observer is called the apparent frequency. It may be less than or greater than the actual frequency emitted by the sound source. The difference depends on the relative motion between the source and observer.
(1) When observer and source are stationary
(i) Sound waves propagate in the form of spherical wavefronts (shown as circles)
(ii) The distance between two successive circles is equal to wavelength \[\lambda \].
Whenever there is a relative motion between a source of sound and the observer (listener), the frequency of sound heard by the observer is different from the actual frequency of sound emitted by the source.
The frequency observed by the observer is called the apparent frequency. It may be less than or greater than the actual frequency emitted by the sound source. The difference depends on the relative motion between the source and observer.
(1) When observer and source are stationary
(i) Sound waves propagate in the form of spherical wavefronts (shown as circles)
(ii) The distance between two successive circles is equal to wavelength \[\lambda \].
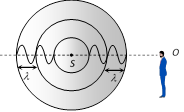 (iii) Number of waves crossing the observer = Number of waves emitted by the source (iv) Thus apparent frequency \[(n')=\] actual frequency \[(n)\].
(2) When source is moving but observer is at rest
(iii) Number of waves crossing the observer = Number of waves emitted by the source (iv) Thus apparent frequency \[(n')=\] actual frequency \[(n)\].
(2) When source is moving but observer is at rest
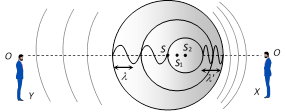 (i) \[{{S}_{1}},\,{{S}_{2}},\,{{S}_{3}}\] are the positions of the source at three different positions.
(ii) Waves are represented by non-concentric circles, they appear compressed in the forward direction and spread out in backward direction.
(iii) For observer (X)
Apparent wavelength \[\lambda '<\] Actual wavelength \[\lambda \]
\[\Rightarrow \] Apparent frequency \[n'>\] Actual frequency \[n\]
For observer (Y) : \[\lambda '>\lambda \]\[\Rightarrow n'<n\]
(3) When source is stationary but observer is moving
(i) \[{{S}_{1}},\,{{S}_{2}},\,{{S}_{3}}\] are the positions of the source at three different positions.
(ii) Waves are represented by non-concentric circles, they appear compressed in the forward direction and spread out in backward direction.
(iii) For observer (X)
Apparent wavelength \[\lambda '<\] Actual wavelength \[\lambda \]
\[\Rightarrow \] Apparent frequency \[n'>\] Actual frequency \[n\]
For observer (Y) : \[\lambda '>\lambda \]\[\Rightarrow n'<n\]
(3) When source is stationary but observer is moving
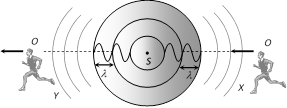 (i) Waves are again represented by concentric circles.
(ii) No change in wavelength received by either observer X or Y.
(iii) Observer X (moving towards) receives wave fronts at shorter interval thus \[n'>n.\]
(iv) Observer Y receives wavelengths at longer interval thus \[n'<n.\]
(4) General expression for apparent frequency : Suppose observed (O) and source (S) are moving in the same direction along a line with velocities \[{{v}_{O}}\] and \[{{v}_{S}}\] respectively. Velocity of sound is v and velocity of medium is \[{{v}_{m}}\] then apparent frequency observed by observer is given by \[n'=\left[ \frac{(v+{{v}_{m}})-{{v}_{0}}}{(v+{{v}_{m}})-{{v}_{S}}} \right]n\]
(i) Waves are again represented by concentric circles.
(ii) No change in wavelength received by either observer X or Y.
(iii) Observer X (moving towards) receives wave fronts at shorter interval thus \[n'>n.\]
(iv) Observer Y receives wavelengths at longer interval thus \[n'<n.\]
(4) General expression for apparent frequency : Suppose observed (O) and source (S) are moving in the same direction along a line with velocities \[{{v}_{O}}\] and \[{{v}_{S}}\] respectively. Velocity of sound is v and velocity of medium is \[{{v}_{m}}\] then apparent frequency observed by observer is given by \[n'=\left[ \frac{(v+{{v}_{m}})-{{v}_{0}}}{(v+{{v}_{m}})-{{v}_{S}}} \right]n\]
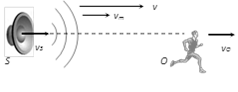 If medium is stationary i.e. \[{{v}_{m}}=0\] then \[n'=n\,\left( \frac{v-{{v}_{O}}}{v-{{v}_{S}}} \right)\]
Sign convection for different situation
(i) The direction of v is always taken from source to observer.
(ii) All the velocities in the direction of v are taken positive.
(iii) All the velocities in the opposite direction of v are taken negative.
If medium is stationary i.e. \[{{v}_{m}}=0\] then \[n'=n\,\left( \frac{v-{{v}_{O}}}{v-{{v}_{S}}} \right)\]
Sign convection for different situation
(i) The direction of v is always taken from source to observer.
(ii) All the velocities in the direction of v are taken positive.
(iii) All the velocities in the opposite direction of v are taken negative. 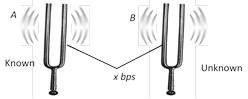 There are two possibilities to known frequency of unknown tuning fork.
\[{{n}_{A}}-{{n}_{B}}=x\] ... (i)
or \[{{n}_{B}}-{{n}_{A}}=x\] ... (ii)
To find the frequency of unknown tuning fork \[({{n}_{B}})\] following steps are taken.
(1) Loading or filing of one prong of known or unknown (by wax) tuning fork, so frequency changes (decreases after loading, increases after filing).
(2) Sound them together again, and count the number of heard beats per sec again, let it be \[x'\]. These are following four condition arises.
(i) \[x'>x\]
(ii) \[x'<x\]
(iii) \[x'=0\]
(iv) \[x'=x\]
(3) With the above information, the exact frequency of the unknown tuning fork can be determined as illustrated below.
Suppose two tuning forks A (frequency \[{{n}_{A}}\] is known) and B (frequency \[{{n}_{B}}\] is unknown) are sounded together and gives \[x\] beats/sec. If one prong of unknown tuning fork B is loaded with a little wax (so \[{{n}_{B}}\] decreases) and it is sounded again together with known tuning fork A, then in the following four given condition \[{{n}_{B}}\] can be determined.
(4) If \[x'>x\] than \[x,\] then this would happen only when the new frequency of B is more away from \[{{n}_{A}}\]. This would happen if originally (before loading), \[{{n}_{B}}\] was less than \[{{n}_{A}}\].
Thus initially \[{{n}_{B}}={{n}_{A}}-x\].
(5) If \[x'<x\] than \[x,\] then this would happen only when the new frequency of B is more nearer to \[{{n}_{A}}\]. This would happen if originally (before loading), \[{{n}_{B}}\] was more than \[{{n}_{A}}\]. Thus initially \[{{n}_{B}}={{n}_{A}}+x\].
(6) If \[x'=x\] then this would means that the new frequency (after loading) differs from \[{{n}_{A}}\] by the same amount as was the old frequency (before loading). This means initially \[{{n}_{B}}={{n}_{A}}+x\]
(and now it has decreased to \[n{{'}_{B}}={{n}_{A}}-x\])
(7) If \[x'=0,\] then this would happen only when the new frequency of B becomes equal to \[{{n}_{A}}\] This would happen if originally \[{{n}_{B}}\] was more than \[{{n}_{A}}\].
Thus initially \[{{n}_{B}}=n+x\].
Frequency of unknown tuning fork for various cases
There are two possibilities to known frequency of unknown tuning fork.
\[{{n}_{A}}-{{n}_{B}}=x\] ... (i)
or \[{{n}_{B}}-{{n}_{A}}=x\] ... (ii)
To find the frequency of unknown tuning fork \[({{n}_{B}})\] following steps are taken.
(1) Loading or filing of one prong of known or unknown (by wax) tuning fork, so frequency changes (decreases after loading, increases after filing).
(2) Sound them together again, and count the number of heard beats per sec again, let it be \[x'\]. These are following four condition arises.
(i) \[x'>x\]
(ii) \[x'<x\]
(iii) \[x'=0\]
(iv) \[x'=x\]
(3) With the above information, the exact frequency of the unknown tuning fork can be determined as illustrated below.
Suppose two tuning forks A (frequency \[{{n}_{A}}\] is known) and B (frequency \[{{n}_{B}}\] is unknown) are sounded together and gives \[x\] beats/sec. If one prong of unknown tuning fork B is loaded with a little wax (so \[{{n}_{B}}\] decreases) and it is sounded again together with known tuning fork A, then in the following four given condition \[{{n}_{B}}\] can be determined.
(4) If \[x'>x\] than \[x,\] then this would happen only when the new frequency of B is more away from \[{{n}_{A}}\]. This would happen if originally (before loading), \[{{n}_{B}}\] was less than \[{{n}_{A}}\].
Thus initially \[{{n}_{B}}={{n}_{A}}-x\].
(5) If \[x'<x\] than \[x,\] then this would happen only when the new frequency of B is more nearer to \[{{n}_{A}}\]. This would happen if originally (before loading), \[{{n}_{B}}\] was more than \[{{n}_{A}}\]. Thus initially \[{{n}_{B}}={{n}_{A}}+x\].
(6) If \[x'=x\] then this would means that the new frequency (after loading) differs from \[{{n}_{A}}\] by the same amount as was the old frequency (before loading). This means initially \[{{n}_{B}}={{n}_{A}}+x\]
(and now it has decreased to \[n{{'}_{B}}={{n}_{A}}-x\])
(7) If \[x'=0,\] then this would happen only when the new frequency of B becomes equal to \[{{n}_{A}}\] This would happen if originally \[{{n}_{B}}\] was more than \[{{n}_{A}}\].
Thus initially \[{{n}_{B}}=n+x\].
Frequency of unknown tuning fork for various cases
| By loading | |||||||||||||||||||
| If B is loaded with wax so its frequency decreases | If A is loaded with wax its frequency decreases | ||||||||||||||||||
| If \[x\] increases \[{{n}_{B}}={{n}_{A}}-x\] | If \[x\] increases \[{{n}_{B}}={{n}_{A}}+x\] | more...||||||||||||||||||
| Closed organ pipe | ||
| Fundamental mode | Third harmonic First over tone | Fifth harmonic Second over tone |
 \[{{n}_{1}}\,=\,\frac{v}{4l}\]
\[{{n}_{1}}\,=\,\frac{v}{4l}\]
|
 \[{{n}_{2}}\,=\,\frac{v}{{{\lambda }_{2}}}\,\,=\,\frac{3v}{4l}\,=3\,{{n}_{1}}\]
\[{{n}_{2}}\,=\,\frac{v}{{{\lambda }_{2}}}\,\,=\,\frac{3v}{4l}\,=3\,{{n}_{1}}\]
|
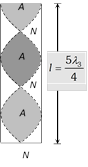 \[{{n}_{3}}\,=\,\frac{5v}{4l}=\,5{{n}_{1}}\]
\[{{n}_{3}}\,=\,\frac{5v}{4l}=\,5{{n}_{1}}\]
|
| Open organ pipe | ||
| Fundamental mode | Second harmonic | Third harmonic |
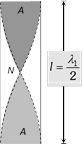 \[{{n}_{1}}=\frac{v}{{{\lambda }_{1}}}=\,\frac{v}{2l}\]
\[{{n}_{1}}=\frac{v}{{{\lambda }_{1}}}=\,\frac{v}{2l}\]
|
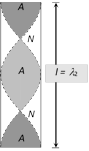 \[{{n}_{2}}=\frac{v}{{{\lambda }_{2}}}=\frac{v}{L}=\,2{{n}_{1}}\]
\[{{n}_{2}}=\frac{v}{{{\lambda }_{2}}}=\frac{v}{L}=\,2{{n}_{1}}\]
|
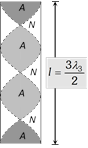 \[{{n}_{3}}=\frac{v}{{{\lambda }_{3}}}=\,\frac{3v}{2l}=3{{n}_{1}}\]
\[{{n}_{3}}=\frac{v}{{{\lambda }_{3}}}=\,\frac{3v}{2l}=3{{n}_{1}}\]
|
 As the frequency of the wave in both strings must be same so
\[\frac{p}{2{{l}_{1}}}=\sqrt{\frac{T}{{{m}_{1}}}}=\frac{q}{2{{l}_{2}}}\sqrt{\frac{T}{{{m}_{2}}}}\]\[\Rightarrow \] \[\frac{p}{q}=\frac{{{l}_{1}}}{{{l}_{2}}}\sqrt{\frac{{{m}_{1}}}{{{m}_{2}}}}=\frac{{{l}_{1}}}{{{l}_{2}}}\sqrt{\frac{{{\rho }_{1}}}{{{\rho }_{2}}}}\]
As the frequency of the wave in both strings must be same so
\[\frac{p}{2{{l}_{1}}}=\sqrt{\frac{T}{{{m}_{1}}}}=\frac{q}{2{{l}_{2}}}\sqrt{\frac{T}{{{m}_{2}}}}\]\[\Rightarrow \] \[\frac{p}{q}=\frac{{{l}_{1}}}{{{l}_{2}}}\sqrt{\frac{{{m}_{1}}}{{{m}_{2}}}}=\frac{{{l}_{1}}}{{{l}_{2}}}\sqrt{\frac{{{\rho }_{1}}}{{{\rho }_{2}}}}\] You need to login to perform this action.
You will be redirected in
3 sec
