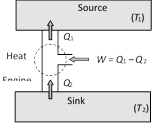
 The working substance takes heat \[{{Q}_{2}}\] from a sink (contents of refrigerator) at lower temperature, has a net amount of work done W on it by an external agent (usually compressor of refrigerator) and gives out a larger amount of heat \[{{Q}_{1}}\] to a hot body at temperature \[{{T}_{1}}\] (usually atmosphere). Thus, it transfers heat from a cold to a hot body at the expense of mechanical energy supplied to it by an external agent. The cold body is thus cooled more and more.
The performance of a refrigerator is expressed by means of "coefficient of performance" \[\beta \] which is defined as the ratio of the heat extracted from the cold body to the work needed to transfer it to the hot body.
i.e. \[\beta =\frac{\text{Heat extracted}}{\text{Work done}}=\frac{{{Q}_{2}}}{W}=\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\]
A perfect refrigerator is one which transfers heat from cold to hot body without doing work
i.e. \[W=0\] so that \[{{Q}_{1}}={{Q}_{2}}\] and hence \[\beta =\infty \]
(1) Carnot refrigerator : For Carnot refrigerator \[\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}\]
\[\Rightarrow \] \[\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{2}}}=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{2}}}\] or \[\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\]
So coefficient of performance \[\beta =\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\]
where \[{{T}_{1}}=\] temperature of surrounding, \[{{T}_{2}}=\] temperature of cold body. It is clear that \[\beta =0\] when \[{{T}_{2}}=0\]
i.e. the coefficient of performance will be zero if the cold body is at the temperature equal to absolute zero.
(2) Relation between coefficient of performance and efficiency of refrigerator
We know \[\beta =\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\]\[=\frac{{{Q}_{2}}/{{Q}_{1}}}{1-{{Q}_{2}}/{{Q}_{1}}}\] ... (i)
But the efficiency \[\eta =1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\] or \[\frac{{{Q}_{2}}}{{{Q}_{1}}}=1-\eta \] ...(ii)
From (i) and (ii) we get, \[\beta =\frac{1-\eta }{\eta }\]
The working substance takes heat \[{{Q}_{2}}\] from a sink (contents of refrigerator) at lower temperature, has a net amount of work done W on it by an external agent (usually compressor of refrigerator) and gives out a larger amount of heat \[{{Q}_{1}}\] to a hot body at temperature \[{{T}_{1}}\] (usually atmosphere). Thus, it transfers heat from a cold to a hot body at the expense of mechanical energy supplied to it by an external agent. The cold body is thus cooled more and more.
The performance of a refrigerator is expressed by means of "coefficient of performance" \[\beta \] which is defined as the ratio of the heat extracted from the cold body to the work needed to transfer it to the hot body.
i.e. \[\beta =\frac{\text{Heat extracted}}{\text{Work done}}=\frac{{{Q}_{2}}}{W}=\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\]
A perfect refrigerator is one which transfers heat from cold to hot body without doing work
i.e. \[W=0\] so that \[{{Q}_{1}}={{Q}_{2}}\] and hence \[\beta =\infty \]
(1) Carnot refrigerator : For Carnot refrigerator \[\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}\]
\[\Rightarrow \] \[\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{2}}}=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{2}}}\] or \[\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\]
So coefficient of performance \[\beta =\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\]
where \[{{T}_{1}}=\] temperature of surrounding, \[{{T}_{2}}=\] temperature of cold body. It is clear that \[\beta =0\] when \[{{T}_{2}}=0\]
i.e. the coefficient of performance will be zero if the cold body is at the temperature equal to absolute zero.
(2) Relation between coefficient of performance and efficiency of refrigerator
We know \[\beta =\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\]\[=\frac{{{Q}_{2}}/{{Q}_{1}}}{1-{{Q}_{2}}/{{Q}_{1}}}\] ... (i)
But the efficiency \[\eta =1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\] or \[\frac{{{Q}_{2}}}{{{Q}_{1}}}=1-\eta \] ...(ii)
From (i) and (ii) we get, \[\beta =\frac{1-\eta }{\eta }\]  The working substance absorbs heat \[{{Q}_{1}}\] from the source, does an amount of work W, returns the remaining amount of heat to the sink and comes back to its original state and there occurs no change in its internal energy.
By repeating the same cycle over and over again, work is continuously obtained.
The performance of heat engine is expressed by means of ?efficiency? \[\eta \] which is defined as the ratio of useful work obtained from the engine to the heat supplied to it.
\[\eta =\frac{\text{Work done}}{\text{Heat input}}=\frac{W}{{{Q}_{1}}}\]
For cyclic process \[\Delta U=0\] hence from FLOT \[\Delta Q=\Delta W\]
So \[W={{Q}_{1}}-{{Q}_{2}}\] \[\Rightarrow \] \[\eta =\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
A perfect heat engine is one which converts all heat into work i.e. \[W={{Q}_{1}}\] so that \[{{Q}_{2}}=0\] and hence\[\eta =1\].
But practically efficiency of an engine is always less than 1.
The working substance absorbs heat \[{{Q}_{1}}\] from the source, does an amount of work W, returns the remaining amount of heat to the sink and comes back to its original state and there occurs no change in its internal energy.
By repeating the same cycle over and over again, work is continuously obtained.
The performance of heat engine is expressed by means of ?efficiency? \[\eta \] which is defined as the ratio of useful work obtained from the engine to the heat supplied to it.
\[\eta =\frac{\text{Work done}}{\text{Heat input}}=\frac{W}{{{Q}_{1}}}\]
For cyclic process \[\Delta U=0\] hence from FLOT \[\Delta Q=\Delta W\]
So \[W={{Q}_{1}}-{{Q}_{2}}\] \[\Rightarrow \] \[\eta =\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
A perfect heat engine is one which converts all heat into work i.e. \[W={{Q}_{1}}\] so that \[{{Q}_{2}}=0\] and hence\[\eta =1\].
But practically efficiency of an engine is always less than 1. | (1) PV-graphs | |
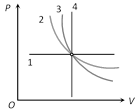 |
1 \[\xrightarrow{\,}\] Isobaric (P-constant) 2\[\xrightarrow{\,}\] Isothermal (Because\[P\propto \frac{1}{V}\]) 3 \[\xrightarrow{\,}\]Adiabatic (Because \[P\propto \frac{1}{{{V}^{\gamma }}}\]) 4 \[\xrightarrow{\,}\] Isochoric (V-constant) |
| (2) PT-graphs | |
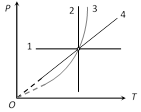 |
1 \[\xrightarrow{\,}\] Isobaric (P-constant) 2 \[\xrightarrow{\,}\] Isothermal (T-constant) 3 \[\xrightarrow{\,}\] Adiabatic (Because\[P\propto {{T}^{\frac{\gamma }{\gamma -1}}}\]) 4 \[\xrightarrow{\,}\] Isochoric (In isochoric \[P\propto T\]) |
| (3) VT-graphs | |
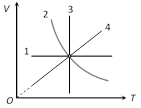 |
1 \[\xrightarrow{\,}\] Isochoric (V-constant) 2 \[\xrightarrow{\,}\] Adiabatic (Because\[V\propto {{T}^{\frac{1}{1-\gamma }}}\]) 3 \[\xrightarrow{\,}\] Isothermal (T-constant) 4 \[\xrightarrow{\,}\] Isobaric (In isobaric \[V\propto T\]) |
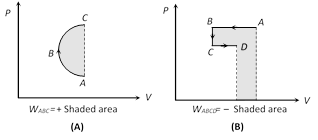
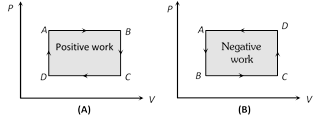 (4) Work done in non cyclic process depends upon the path chosen or the series of changes involved and can be calculated by the area covered between the curve and volume axis on PV diagram.
(4) Work done in non cyclic process depends upon the path chosen or the series of changes involved and can be calculated by the area covered between the curve and volume axis on PV diagram.
| Type of gas | \[P\propto \frac{1}{{{V}^{\gamma }}}\] | \[P\propto {{T}^{\frac{\gamma }{\gamma -1}}}\] | \[T\propto \frac{1}{{{V}^{\gamma -1}}}\] |
| Monoatomic \[\gamma =5/3\] | \[P\propto \frac{1}{{{V}^{5/3}}}\] | \[P\propto {{T}^{5/2}}\] | \[T\propto \frac{1}{{{V}^{2/3}}}\] |
| Diatomic \[\gamma =7/5\] | \[P\propto \frac{1}{{{V}^{7/5}}}\] | \[P\propto {{T}^{7/2}}\] | \[T\propto \frac{1}{{{V}^{2/5}}}\] |
| Polyatomic \[\gamma =4/3\] | \[P\propto \frac{1}{{{V}^{4/3}}}\] | \[P\propto {{T}^{4}}\] | \[T\propto \frac{1}{{{V}^{1/3}}}\] |
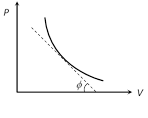 \[\therefore \] Slope of adiabatic curve\[\tan \varphi =-\gamma \left( \frac{P}{V} \right)\]
(iii) But we also know that slope of isothermal curve \[\tan \theta =\frac{-P}{V}\]
Hence \[{{\text{(Slope)}}_{\text{Adi}}}=\gamma \times {{\text{(Slope)}}_{\text{Iso}}}\] or \[\frac{{{\text{(Slope)}}_{\text{Adi}}}}{{{\text{(Slope)}}_{\text{Iso}}}}>1\]
(6) Specific heat : Specific heat of a gas during adiabatic change is zero As \[C=\frac{Q}{m\Delta T}=\frac{0}{m\Delta T}=0\] [As Q = 0]
(7) Adiabatic elasticity \[({{E}_{\phi }}):\] \[P{{V}^{\gamma }}=\text{constant}\]
Differentiating both sides \[d\,P{{V}^{\gamma }}+P\gamma {{V}^{\gamma -1}}dV=0\]
\[\gamma P=\frac{dP}{-dV/V}=\frac{\text{Stress}}{\text{Strain}}={{E}_{\varphi }}\]\[\Rightarrow \]\[{{E}_{\varphi }}=\gamma P\]
i.e. adiabatic elasticity is g times that more...
\[\therefore \] Slope of adiabatic curve\[\tan \varphi =-\gamma \left( \frac{P}{V} \right)\]
(iii) But we also know that slope of isothermal curve \[\tan \theta =\frac{-P}{V}\]
Hence \[{{\text{(Slope)}}_{\text{Adi}}}=\gamma \times {{\text{(Slope)}}_{\text{Iso}}}\] or \[\frac{{{\text{(Slope)}}_{\text{Adi}}}}{{{\text{(Slope)}}_{\text{Iso}}}}>1\]
(6) Specific heat : Specific heat of a gas during adiabatic change is zero As \[C=\frac{Q}{m\Delta T}=\frac{0}{m\Delta T}=0\] [As Q = 0]
(7) Adiabatic elasticity \[({{E}_{\phi }}):\] \[P{{V}^{\gamma }}=\text{constant}\]
Differentiating both sides \[d\,P{{V}^{\gamma }}+P\gamma {{V}^{\gamma -1}}dV=0\]
\[\gamma P=\frac{dP}{-dV/V}=\frac{\text{Stress}}{\text{Strain}}={{E}_{\varphi }}\]\[\Rightarrow \]\[{{E}_{\varphi }}=\gamma P\]
i.e. adiabatic elasticity is g times that more...  \[{{T}_{1}}
\[{{T}_{1}} 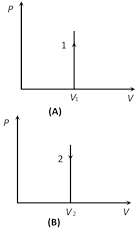 (i) Isometric heating
(a) Pressure \[\xrightarrow{\,}\] increases
(b) Temperature \[\xrightarrow{\,}\] increases
(c) \[\Delta Q\] \[\xrightarrow{\,}\]positive
(d) \[\Delta U\] \[\xrightarrow{\,}\]positive
(ii) Isometric cooling
(a) Pressure \[\xrightarrow{\,}\] decreases
(b) Temperature \[\xrightarrow{\,}\] decreases
(c) \[\Delta Q\] \[\xrightarrow{\,}\]negative
(d) \[\Delta U\]\[\xrightarrow{\,}\]negative
(3) Specific heat : Specific heat of gas during isochoric process \[{{C}_{V}}=\frac{f}{2}R\]
(4) Bulk modulus of elasticity : \[K=\frac{\Delta P}{\frac{-\Delta V}{V}}=\frac{\Delta P}{0}=\infty \]
(5) Work done in isochoric process \[\Delta W=P\Delta V=P[{{V}_{f}}-{{V}_{i}}]=0\] [As V = constant]
(6) FLOT in isochoric process : From \[\Delta Q=\Delta U+\Delta W\]
\[\because \] \[\Delta W=0\Rightarrow {{(\Delta Q)}_{V}}=\Delta U=\mu {{C}_{V}}\,\Delta T=\mu \frac{R}{\gamma -1}\Delta T=\frac{{{P}_{f}}{{V}_{f}}-{{P}_{i}}{{V}_{i}}}{\gamma -1}\]
(i) Isometric heating
(a) Pressure \[\xrightarrow{\,}\] increases
(b) Temperature \[\xrightarrow{\,}\] increases
(c) \[\Delta Q\] \[\xrightarrow{\,}\]positive
(d) \[\Delta U\] \[\xrightarrow{\,}\]positive
(ii) Isometric cooling
(a) Pressure \[\xrightarrow{\,}\] decreases
(b) Temperature \[\xrightarrow{\,}\] decreases
(c) \[\Delta Q\] \[\xrightarrow{\,}\]negative
(d) \[\Delta U\]\[\xrightarrow{\,}\]negative
(3) Specific heat : Specific heat of gas during isochoric process \[{{C}_{V}}=\frac{f}{2}R\]
(4) Bulk modulus of elasticity : \[K=\frac{\Delta P}{\frac{-\Delta V}{V}}=\frac{\Delta P}{0}=\infty \]
(5) Work done in isochoric process \[\Delta W=P\Delta V=P[{{V}_{f}}-{{V}_{i}}]=0\] [As V = constant]
(6) FLOT in isochoric process : From \[\Delta Q=\Delta U+\Delta W\]
\[\because \] \[\Delta W=0\Rightarrow {{(\Delta Q)}_{V}}=\Delta U=\mu {{C}_{V}}\,\Delta T=\mu \frac{R}{\gamma -1}\Delta T=\frac{{{P}_{f}}{{V}_{f}}-{{P}_{i}}{{V}_{i}}}{\gamma -1}\] 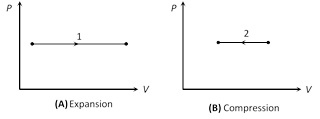 Slope =\[\frac{dP}{dV}=0\] Slope = \[\frac{dP}{dV}=0\]
(i) In isobaric expansion (Heating)
Temperature \[\xrightarrow{\,\,\,\,}\] increases so \[\Delta U\] is positive
Volume \[\xrightarrow{\,\,\,\,}\] increases so \[\Delta W\] is positive
Heat \[\xrightarrow{\,\,\,\,}\] flows into the system so \[\Delta Q\] is positive
(ii) In isobaric compression (Cooling)
Temperature \[\xrightarrow{\,\,\,\,}\] decreases so \[\Delta U\] is negative
Volume \[\xrightarrow{\,\,\,\,}\] decreases so \[\Delta W\] is negative
Heat \[\xrightarrow{\,\,\,\,}\] flows out from the system so \[\Delta Q\] is negative
(3) Specific heat : Specific heat of gas during isobaric process \[{{C}_{P}}=\left( \frac{f}{2}+1 \right)R\]
(4) Bulk modulus of elasticity : \[K=\frac{\Delta P}{\frac{-\Delta V}{V}}=0\] [As \[\Delta P=0\]]
(5) Work done in isobaric process
\[\Delta W=\int_{{{V}_{i}}}^{{{V}_{f}}}{P\,dV}=P\int_{{{V}_{i}}}^{{{V}_{f}}}{dV}=P[{{V}_{f}}-{{V}_{i}}]\] [As P = constant]
\[\Rightarrow \] \[\Delta W=P({{V}_{f}}-{{V}_{i}})=\mu R[{{T}_{f}}-{{T}_{i}}]=\mu R\,\Delta T\]
(6) FLOT in isobaric process : From \[\Delta Q=\Delta U+\Delta W\]
\[\because \] \[\Delta U=\mu \,{{C}_{V}}\,\Delta T\]\[=\mu \frac{R}{(\gamma -1)}\Delta T\] and \[\Delta W=\mu R\,\Delta T\]
\[\Rightarrow \] \[{{(\Delta Q)}_{P}}=\mu \frac{R}{(\gamma -1)}\Delta T+\mu R\,\Delta T\]\[=\mu \left( \frac{\gamma }{\gamma -1} \right)R\,\Delta T\]\[=\mu \,{{C}_{P}}\,\Delta T\]
(7) Examples of isobaric process : All state changes occurs at constant temperature and pressure.
Boiling of water
Slope =\[\frac{dP}{dV}=0\] Slope = \[\frac{dP}{dV}=0\]
(i) In isobaric expansion (Heating)
Temperature \[\xrightarrow{\,\,\,\,}\] increases so \[\Delta U\] is positive
Volume \[\xrightarrow{\,\,\,\,}\] increases so \[\Delta W\] is positive
Heat \[\xrightarrow{\,\,\,\,}\] flows into the system so \[\Delta Q\] is positive
(ii) In isobaric compression (Cooling)
Temperature \[\xrightarrow{\,\,\,\,}\] decreases so \[\Delta U\] is negative
Volume \[\xrightarrow{\,\,\,\,}\] decreases so \[\Delta W\] is negative
Heat \[\xrightarrow{\,\,\,\,}\] flows out from the system so \[\Delta Q\] is negative
(3) Specific heat : Specific heat of gas during isobaric process \[{{C}_{P}}=\left( \frac{f}{2}+1 \right)R\]
(4) Bulk modulus of elasticity : \[K=\frac{\Delta P}{\frac{-\Delta V}{V}}=0\] [As \[\Delta P=0\]]
(5) Work done in isobaric process
\[\Delta W=\int_{{{V}_{i}}}^{{{V}_{f}}}{P\,dV}=P\int_{{{V}_{i}}}^{{{V}_{f}}}{dV}=P[{{V}_{f}}-{{V}_{i}}]\] [As P = constant]
\[\Rightarrow \] \[\Delta W=P({{V}_{f}}-{{V}_{i}})=\mu R[{{T}_{f}}-{{T}_{i}}]=\mu R\,\Delta T\]
(6) FLOT in isobaric process : From \[\Delta Q=\Delta U+\Delta W\]
\[\because \] \[\Delta U=\mu \,{{C}_{V}}\,\Delta T\]\[=\mu \frac{R}{(\gamma -1)}\Delta T\] and \[\Delta W=\mu R\,\Delta T\]
\[\Rightarrow \] \[{{(\Delta Q)}_{P}}=\mu \frac{R}{(\gamma -1)}\Delta T+\mu R\,\Delta T\]\[=\mu \left( \frac{\gamma }{\gamma -1} \right)R\,\Delta T\]\[=\mu \,{{C}_{P}}\,\Delta T\]
(7) Examples of isobaric process : All state changes occurs at constant temperature and pressure.
Boiling of water
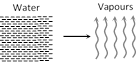 (i) Water \[\xrightarrow{\,}\] vapours
(ii) Temperature \[\xrightarrow{{}}\] constant
(iii) Volume \[\xrightarrow{\,}\]increases
(iv) A part of heat supplied is used to change volume (expansion) against external pressure and remaining part is used to increase it's potential energy (kinetic energy remains constant)
(v) From FLOT \[\Delta Q=\Delta U+\Delta W\Rightarrow mL=\Delta U+P({{V}_{f}}-{{V}_{i}})\]
Freezing of water
(i) Water \[\xrightarrow{\,}\] vapours
(ii) Temperature \[\xrightarrow{{}}\] constant
(iii) Volume \[\xrightarrow{\,}\]increases
(iv) A part of heat supplied is used to change volume (expansion) against external pressure and remaining part is used to increase it's potential energy (kinetic energy remains constant)
(v) From FLOT \[\Delta Q=\Delta U+\Delta W\Rightarrow mL=\Delta U+P({{V}_{f}}-{{V}_{i}})\]
Freezing of water
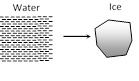 (i) Water \[\xrightarrow{\,}\] ice
(ii) Temperature \[\xrightarrow{\,}\] constant
(iii) Volume \[\xrightarrow{\,}\]increases
(iv) Heat is given by water it self. It is used to do work against external atmospheric pressure and to decreases the internal potential energy.
(v) From FLOT \[\Delta Q=\Delta U+\Delta W\Rightarrow -mL=\Delta U+P({{V}_{f}}{{V}_{i}})\]
(i) Water \[\xrightarrow{\,}\] ice
(ii) Temperature \[\xrightarrow{\,}\] constant
(iii) Volume \[\xrightarrow{\,}\]increases
(iv) Heat is given by water it self. It is used to do work against external atmospheric pressure and to decreases the internal potential energy.
(v) From FLOT \[\Delta Q=\Delta U+\Delta W\Rightarrow -mL=\Delta U+P({{V}_{f}}{{V}_{i}})\] You need to login to perform this action.
You will be redirected in
3 sec
