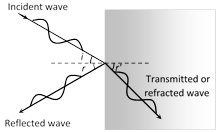
(3) For reflection angle of incidence (i) = Angle of reflection (r)
(4) In case of refraction or transmission \[\frac{\sin i}{\sin r'}\,=\,\frac{{{v}_{i}}}{{{v}_{t}}}\]
(5) Boundary conditions : Reflection of a wave pulse from some boundary depends on the nature of the boundary.
(i) Rigid end : When the incident wave reaches a fixed end, it exerts an upward pull on the end, according to Newton's law the fixed end exerts an equal and opposite down ward force on the string. It result an inverted pulse or phase change of \[\pi \]. Crest (C) reflects as trough (T) and vice-versa, Time changes by \[\frac{T}{2}\] and Path changes by \[\frac{\lambda }{2}\]
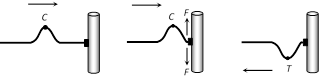(ii) Free end : When a wave or pulse is reflected from a free end, then there is no change of phase (as there is no reaction force). Crest (C) reflects as crest (C) and trough (T) reflects as trough (T), Time changes by zero and Path changes by zero.
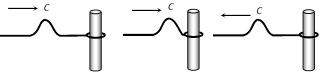(iii) Exception : Longitudinal pressure waves suffer no change in phase from rigid end i.e. compression pulse reflects as compression pulse. On the other hand if longitudinal pressure wave reflects from free end, it suffer a phase change of \[\pi \] i.e. compression reflects as rarefaction and vice-versa.
(iv) Effect on different variables : In case of reflection, because medium is same and hence, speed, frequency \[(\omega )\] and wavelength \[\lambda \] (or k) do not changes. On the other hand in case of transmitted wave since medium changes and hence speed, wavelength (or k) changes but frequency \[(\omega )\] remains the same.
(6) Wave in a combination of string
(i) Wave goes from rarer to denser medium
Incident wave \[{{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)\]
Reflected wave \[{{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+\pi ]\]\[=-\,a\sin \,(\omega \,t+{{k}_{1}}x)\]
Transmitted wave\[{{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)\]
(ii) Wave goes from denser to rarer medium
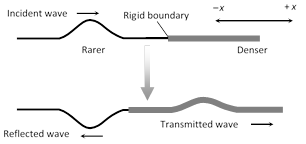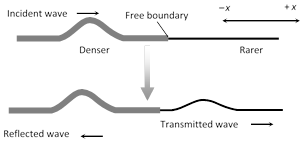Incident wave \[{{y}_{i}}={{a}_{i}}\sin (\omega \,t-{{k}_{1}}x)\]
Reflected wave \[{{y}_{r}}={{a}_{r}}\sin [\omega \,t-{{k}_{1}}(-x)+0]\]\[=\,a\sin \,(\omega \,t+{{k}_{1}}x)\]
Transmitted wave\[{{y}_{t}}={{a}_{t}}\sin \,(\omega \,t-{{k}_{2}}x)\]
(iii) Ratio of amplitudes : It is given as follows
\[\frac{{{a}_{r}}}{{{a}_{i}}}=\frac{{{k}_{1}}-{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}=\frac{{{v}_{2}}-{{v}_{1}}}{{{v}_{2}}+{{v}_{1}}}\]
and \[\frac{{{a}_{t}}}{{{a}_{i}}}=\frac{2{{k}_{1}}}{{{k}_{1}}+{{k}_{2}}}=\frac{2{{v}_{2}}}{{{v}_{1}}+{{v}_{2}}}\]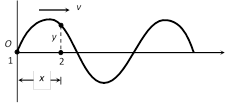 
The displacement y of a particle 1 at O from its mean position at any time t is given by \[y=a\sin \omega \,t.\]
The wave reaches the particle 2 after time \[t=\frac{x}{v}\]. Hence displacement y of a particle 2 is given by
\[y=a\sin \omega \,\left( t-\frac{x}{v} \right)\]\[=a\sin (\omega \,t-kx)\] \[\left( \because \,k=\frac{\omega }{v} \right)\]
The general equation of a plane progressive wave with initial phase is
(3) Various forms of progressive wave function.
(i) \[y=a\,\sin \,(\theta t-kx)\]
(ii) \[y=a\,\sin \,(\omega t-\frac{2\pi }{\lambda }x)\]
(iii) \[y=a\sin 2\pi \left[ \frac{t}{T}-\frac{x}{\lambda } \right]\]
(iv) \[y=a\sin \frac{2\pi }{T}\left( t-x\frac{T}{\lambda } \right)\]
(v) \[y=a\sin \frac{2\pi }{\lambda }(vt-x)\]
(vi) y = \[a\sin \omega \,\left( t-\frac{x}{v} \right)\]
(4) Particle velocity : The rate of change of displacement y w.r.t. time t is known as particle velocity
Hence from \[y=a\sin \,(\omega \,t-kx)\]
Particle velocity \[{{v}_{p}}=\frac{\partial y}{\partial t}=a\omega \,\cos (\omega \,t-kx)\]
Maximum particle velocity \[{{({{v}_{p}})}_{\max }}=a\omega \]
Also \[\frac{\partial y}{\partial t}=-\frac{\omega }{k}\times \frac{\partial y}{\partial x}\]\[\Rightarrow \]\[{{\upsilon }_{p}}=-v\times \] Slope of wave at that point
(5) Important relations for numerical solving
(i) Angular frequency \[\omega =\] co-efficient of \[t\]
(ii) Propagation constant \[k=\] co-efficient of \[x\]
Wave speed \[v=\frac{\text{co-efficient of }t}{\text{co-efficient of }x}=\frac{\omega }{k}\]
(iii) Wave length \[\lambda =\frac{\text{co-efficient of }x}{2\pi }\]
(iv) Time period \[T=\frac{2\pi }{\text{co-efficient of }t}\]
(v) Frequency \[n=\frac{\text{co-efficient of }t}{2\pi }\]
(vi) \[{{({{v}_{p}})}_{\max }}=a\omega =a(2\pi n)=\frac{a2\pi }{T}\]
(vii) If the sign between t and x terms is negative the wave is propagating along positive X-axis and if the sign is positive then the wave moves in negative X-axis direction.
(viii) Co-efficient of sin or cos functions i.e. Argument of sin or cos function is represented by phase i.e. \[(\omega t-kx)=\]Phase.
(ix) Phase difference and path difference : At any instant t, if \[{{\phi }_{1}}\] and \[{{\phi }_{2}}\] are the phases of two particles whose distances from the origin are \[{{x}_{1}}\] and \[{{x}_{2}}\] respectively then \[{{\varphi }_{1}}=(\omega \,t-k{{x}_{1}})\] and \[{{\varphi }_{2}}=(\omega \,t-k{{x}_{2}})\]\[\Rightarrow \]\[{{\varphi }_{1}}-{{\varphi }_{2}}=k({{x}_{2}}-{{x}_{1}})\]
\[\Rightarrow \]Phase difference \[(\Delta \varphi )=\frac{2\pi }{\lambda }\text{.}\,\text{Path difference (}\Delta x)\] \[(x)\]
(x) Phase difference and time difference : If the phases of a particle distance \[x\] from the origin is \[{{\phi }_{1}}\] at time \[t\] and \[{{\phi }_{2}}\] at time \[{{t}_{2}},\] then \[{{\varphi }_{1}}=(\omega \,{{t}_{1}}-kx)\] and \[{{\varphi }_{1}}=(\omega {{t}_{2}}-kx)\]\[\Rightarrow \] \[{{\varphi }_{1}}-{{\varphi }_{2}}=\omega ({{t}_{1}}-{{t}_{2}})\]
\[\Rightarrow \]Phase difference \[(\Delta \varphi )=\frac{2\pi }{T}.\,\text{Time difference}\,\text{(}\Delta t)\] 
(6) Sound of any frequency or wavelength travels through a given medium with the same velocity.
For a given medium velocity remains constant. All other factors like phase, loudness pitch, quality etc. have practically no effect on sound velocity.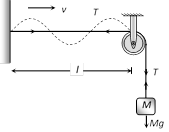 
\[T=Mg\]
\[\Rightarrow \] \[v=\sqrt{\frac{Mg}{m}}\]
(3) If suspended weight is immersed in a liquid of density \[\sigma \] and \[\rho =\] density of material of the suspended load then
\[T=Mg\left( 1-\frac{\sigma }{\rho } \right)\]
\[\Rightarrow \] \[v=\sqrt{\frac{Mg(1-\sigma /\rho )}{m}}\]
(4) If two rigid supports of stretched string are maintained at temperature difference of \[\Delta \theta \] then due to elasticity of string.
\[T=YA\alpha \Delta \theta \]
\[\Rightarrow \]\[v=\sqrt{\frac{YA\alpha \Delta \theta }{m}}\]
\[=\sqrt{\frac{Y\alpha \Delta \theta }{d}}\]
where Y = Young's modulus of elasticity of string, A = Area of cross section of string, \[\alpha =\] Temperature coefficient of thermal expansion, d = Density of wire \[=\frac{m}{A}\]
(5) In a solid body : \[v\,=\,\sqrt{\frac{\eta }{\rho }}\]
where \[\eta =\] Modulus of rigidity; \[\rho =\]Density of the material. 
(3) Frequency (n) : Frequency of vibration of a particle is defined as the number of vibrations completed by particle in one second.
It is the number of complete wavelengths traversed by the wave in one second. Units of frequency are hertz (Hz) and per second.
(4) Time period (T) : Time period of vibration of particle is defined as the time taken by the particle to complete one vibration about its mean position.
It is the time taken by the wave to travel a distance equal to one wavelength
Time period = 1/Frequency Þ T = 1/n
(5) Wave pulse : It is a short wave produced in a medium when the disturbance created for a short time.
(6) Wave train : A series of wave pulse is called wave train.
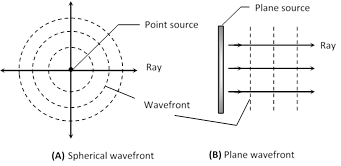
(7) Wave front : A wave front is a line or surface on which the disturbance has the same phase at all points. If the source is periodic, it produces a succession of wave front, all of the same shape. Ripples on a pond are the example of wave fronts.
(8) Wave function ; It is a mathematical description of the disturbance created by a wave. For a string, the wave function is a displacement for sound waves. It is a pressure or density fluctuation where as for light waves it is electric or magnetic field.
Now let us consider a one dimensional wave travelling along x-axis. During wave motion, a particle with equilibrium position x is displaced some distance y in the direction perpendicular to the x-axis. In this case y is a function of position (x) and time (t).
i.e. \[y=f(x,\,t)\]. This is called wave function .
Let the wave pulse is travelling with a speed v, after a time t, the pulse reaches a distance vt along the +x-axis as shown. The wave function now can be represented as \[y=f(x-vt)\]
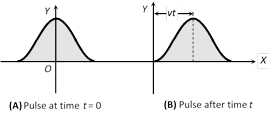If the wave pulse is travelling along \[-x-\]axis then \[y=f(x+vt)\]
If order of a wave function to represent a wave, the three quantities x, v, t must appear in combinations \[(x+vt)\] or \[(x-vt)\]
Thus \[y={{(x-vt)}^{2}},\,\,\sqrt{x-\upsilon t},\,A{{e}^{-B{{(x-vt)}^{2}}}}\] etc. represents travelling waves while \[y=({{x}^{2}}-{{v}^{2}}{{t}^{2}}),\,(\sqrt{x}-\sqrt{vt})\], \[A\sin \text{ }(4{{x}^{2}}\text{ }9{{t}^{2}})\] etc. doesn't represents a wave.
(9) Harmonic wave : If a travelling wave is a sin or cos more... | Transverse waves | Longitudinal waves | ||||||||||||
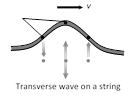
Particles of the medium vibrates in a direction perpendicular to the direction of propagation of wave.
|
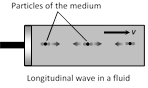
Particles of a medium vibrate in the direction of wave motion.
|
||||||||||||
It travels in the form of crests (C) and troughs (T).
|
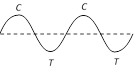
It travels in the form of compression (C) and rarefaction (R).
|
||||||||||||
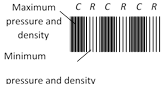
Transverse waves can be transmitted through solids, they can be setup on the surface of liquids. But they can not be transmitted into liquids and gases.
|
These waves can be transmitted through solids, liquids and gases because for these waves propagation, volume elasticity is necessary.
|
||||||||||||
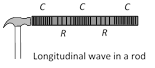
| Medium should posses the property of rigidity | Medium should posses the property of more...
(1) When a wave motion passes through a medium, particles of the medium only vibrate simple harmonically about their mean position. They do leave their position and move with the disturbance.
(2) In wave motion, the phase of particles of medium keeps on changing.
(3) The velocity of the particle during their vibration is different at different position.
(4) The velocity of wave motion through a particular medium is constant. It depends only on the nature of medium not on the frequency, wavelength or intensity.
(5) Energy is propagated along with the wave motion without any net transport of the medium.
(6) For the propagation of wave, a medium should have following characteristics.
(i) Elasticity : So that particles can return to their mean position, after having been.
(ii) Inertia : So that particles can store energy and overshoot their mean position.
(iii) Minimum friction amongst the particles of the medium.
(iv) Uniform density of the medium.
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |
