(1) Factors affecting the value of electronegativity
(i) The size of the atom.
(ii) Electronic configuration. Small atoms attract electrons more than the larger one and are therefore more electronegative. Secondly, atoms with nearly filled shell of electrons, will tend to have higher electronegativity than those sparsely occupied ones.
(2) Variation of electronegativity in the periodic table
(i) In a period, electronegativity increases from left to right. This is due to decrease in size and increase in nuclear charge. Thus the alkali metals possess the lowest value, while the halogens have the highest. Inert gases have zero electronegativity.
(ii) In a group, electronegativity decreases from top to bottom. This is due to increase in atomic size.
If an element exhibits various oxidation state, the atom in the higher oxidation state will be more negative due to greater attraction for the electron, e.g., Sn II (1.30) and Sn IV (1.90).
(3) Electronegativity may be expressed on the following three scales
(i) Mulliken's scale : Mulliken regarded electronegativity as the average value of ionization potential and electron affinity of an atom.
\[\text{Electronegativity}=\frac{\text{Ionization}\,\text{potential}\,+\,\text{Electron}\,\text{affinity}}{\text{2}}\]
(ii) Allred-Rochow scale : Allred and Rochow defined electronegativity as the electrostatic force exerted by the nucleus on the valence electrons. Thus \[\chi =\frac{0.359\,Z}{{{r}^{2}}}+0.744\] where Z is the effective nuclear charge and r is the covalent radius of the atom in Å.
(iii) Pauling scale : Pauling scale of electronegativity is the most widely used. It is based on excess bond energies. He determined electronegativity difference between the two atoms and then by assigning arbitrary values to few elements (e.g. 4.00 to fluorine, 2.5 to carbon and 2.1 to hydrogen), he calculated the electronegativity of the other elements. \[{{\chi }_{A}}-{{\chi }_{B}}=0.208\,\sqrt{\Delta E}\] where \[{{\chi }_{A}}\] and \[{{\chi }_{B}}\] are electronegativities of the atoms A and B respectively, the factor 0.208 arises from the conversion of kcal to electron volt (1 eV = 23.0 kcal/mole),
while \[\Delta E=\]Actual bond energy \[-\sqrt{({{E}_{A-A}}\times {{E}_{B-B}})}\]
Pauling and Mulliken values of electronegativities are related as below \[\chi \] (Pauling) = \[0.34\chi \] (Mulliken) - 0.2
(4) Importance of electronegativity : The following predictions can be made from value of electronegativity,
(i) Nature of the bond between two atoms can be predicted from the eelctronegativity difference of the two atoms.
(a) The difference \[{{X}_{A}}-{{X}_{B}}=0,\] i.e., \[{{X}_{A}}={{X}_{B}}\] the bond is purely covalent.
(b) The difference \[{{X}_{A}}-{{X}_{B}}\] is small, i.e., \[{{X}_{A}}>{{X}_{B}}\], the bond is polar covalent.
(c) The difference \[{{X}_{A}}-{{X}_{B}}\] is 1.7, the bond more... | Li 5.4 eV | Na 1. eV | K 4.3 eV | Rb 4.2 eV | Cs 3.9 eV |
| Li 5.4eV | Be 9.3eV | B 8.3eV | C 11.3eV | N 14.6 eV | O 13.6eV |
| 3Li | 4Be | 5B | 6C | 7N | 8O | 9F | 10Ne |
| 1.23 | 0.89 | 0.80 | 0.77 | 0.74 | 0.74 | 0.72 | more...
Due to screening effect the valency electron experiences less attraction towards nucleus. This brings decrease in the nuclear charge (Z) actually present on the nucleus. The reduced nuclear charge is termed effective nuclear charge and is represented by \[{{Z}^{*}}\]. It is related to actual nuclear charge (Z) by the following formula,
\[{{Z}^{*}}=(Z-\sigma )\] where \[\sigma \] is screening constant.
It is observed that magnitude of effective nuclear charge increases in a period when we move from left to right.
In a subgroup of normal elements the magnitude of effective nuclear charge remains almost the same.
A valence-electron in a multi-electron atom is attracted by the nucleus, and repelled by the electrons of inner-shells. The combined effect of this attractive and repulsive force acting on the valence-electron experiences less attraction from the nucleus. This is called shielding or screening effect. The magnitude of the screening effect depends upon the number of inner electrons, i.e., higher the number of inner electrons, greater shall be the value of screening effect. The screening effect constant is represented by the symbol \['\sigma '\] is determined by the Slater's rules.
The magnitude of screening constant in the case of s- and p- block elements increases in a period as well as in a group as the atomic number increases.
''The repetition of similar electronic configuration after a definite period is the cause of periodicity of the properties of elements.''
It can be explained with the help of electronic arrangement of elements. According to the modern views, the valency of an element is indicated by the number of electrons present in the outermost orbit. The chemical properties of elements are dependent on valency electrons. Variation in electronic arrangement leads to the variation in properties. After a definite interval, recurrence of similar electronic arrangement takes place when the number of valency electrons is the same. Thus, there is a regular gradation and repetition in the properties of elements.
Periodic properties are directly or indirectly related to their electronic configuration and show a regular gradation on moving from left to right in a period or from top to bottom in a group. Some period or from top to bottom in a group. Some important periodic properties are : oxidation number, shielding effect, atomic radii, ionization energy, electron affinity, electro-negativity, valency, density, m.pt. and b.pt.
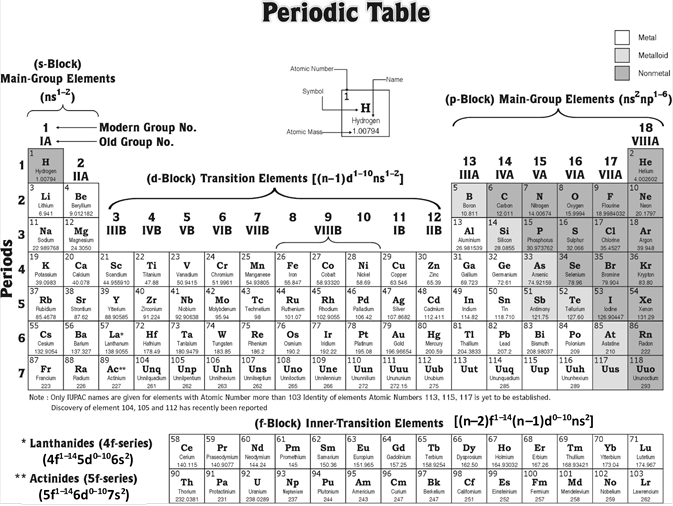
Modern periodic table is also called long form of the periodic table or Bohr?s table. In this table, the elements are arranged in order of their increasing atomic number. It consists of 4 blocks (s, p, d and f), 18 groups numbered from 1 to 18 and 7 periods numbered from 1 to 7.
Blocks : The periodic table is divided into four main blocks (s, p, d and f) depending upon the subshell to which the valence electron enters into.
(1) Elements of group 1 and 2 constitute s-Block.
(2) Elements of group 13, 14, 15, 16, 17, 18 constitute p-Block
(3) Elements of group 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 constitute d-Block
(4) The f-Block elements comprise two horizontal rows placed at the bottom of the periodic table to avoid its unnecessary expansion.
Elements of s- and p-blocks are called normal or representative elements, those of d-block are called transition elements while the f-block elements are called inner transition elements.
Groups : The 18 vertical columns are called groups. The elements belonging to a particular group is known as a family and is usually named after the first number. Apart from this some of the groups are given typical names as examplified beneath,
(1) Elements of group 1 are called Alkali-Metals.
(2) Elements of group 2 are called Alkaline Earths.
(3) Elements of group 3 are called Pnicogens.
(4) Elements of group 16 are called Chalcogens.
(5) Elements of group 17 are called Halogens.
(6) Elements of group 18 are called Noble Gases or Aerogens.
All the other groups are named after the first member of each group.
Periods : The horizontal rows are called periods. There are seven periods in the long form of the periodic table,
(1) Ist period \[_{1}H{{\to }_{2}}He)\] contains 2 elements. It is the shortest period.
(2) 2nd period \[{{(}_{3}}Li{{\to }_{10}}Ne)\] and 3rd period \[{{(}_{11}}Na{{\to }_{18}}Ar)\] contains 8 elements each. These are short periods.
(3) 4th period \[{{(}_{19}}K{{\to }_{36}}Kr)\] and 5th period \[{{(}_{37}}Rb{{\to }_{54}}Xe)\] contains 18 elements each. These are long periods.
(4) 6th period \[{{(}_{55}}Cs{{\to }_{86}}Ra)\] consists of 32 elements and is the longest period.
(5) 7th period starting with \[_{87}Fr\] is incomplete and consists of 19 elements.
According to Bohr the element have been grouped into four types
(1) Inert gases : These atom have been full fill outer most s and p subshell and having the configuration \[n{{s}^{2}}n{{p}^{6}}\] (Exception helium having \[1{{s}^{2}}\]) due to stable configuration these element do not show chemical activity under normal condition and thus termed as inert gases. Under special conditions, the higher members do form some compounds with other elements and hence, the name has been changed to Noble gases. Six element \[He,\ Ne,\ Ar,\ Kr,\ Xe\]and \[Rn\]belongs to this group.
(2) Representative or normal elements : Element in which atom have all shells complete except outermost shell which is incomplete. The number of electrons in the outermost shell varies from 1 to 7 i.e. the configuration of the outermost shell varies from \[n{{s}^{1}}\]to \[n{{s}^{2}}n{{p}^{5}}\]. These consist of some metals, all non metals and metalloid. These are the elements which are found in nature in abundance and active in nature. On account of this, these elements are called representative elements. All the three types of valencies are observed in the case of these elements. These elements have one of the following configuration in their outermost shell.
\[\underset{1}{\mathop{n{{s}^{1}}}}\,\]\[\underset{2}{\mathop{n{{s}^{2}}}}\,\] \[\underset{2}{\mathop{n{{s}^{2}}n{{p}^{1}}}}\,\]\[\underset{4}{\mathop{n{{s}^{2}}n{{p}^{2}}}}\,\] \[\underset{5}{\mathop{n{{s}^{2}}n{{p}^{3}}}}\,\]\[\underset{6}{\mathop{n{{s}^{2}}n{{p}^{4}}}}\,\]\[\underset{7}{\mathop{n{{s}^{2}}n{{p}^{5}}}}\,\]
The number of electrons present in the outermost shell signify the group to which these element belong.
(3) Transition elements : In the atoms of these elements the outermost shell and the penultimate shell (Next to the outermost) are incomplete. These elements have the general configuration \[(n-1)\ {{d}^{1-9}}\]\[n{{s}^{0\ \text{or}\ \text{1}\ \text{or}\ \text{2}}}\]either in the ground state or in excited state. These elements are present in \[I{{V}^{th}},{{V}^{th}},V{{I}^{th}}\]and \[VI{{I}^{th}}\] period of periodic table and called transition elements. There are four transition series every series consists 9 elements each.
(4) Inner transition elements : Atoms of these elements have three outermost shell incomplete. The general configuration is \[(n-2)\ {{f}^{1-14}}(n-1)\ {{d}^{0\ \text{or 1}}}n{{s}^{2}}\]. There are two series of elements.
(i) Lanthanides or rare earths from \[Ce(58)\] to \[Lu(71)\].
(ii) Actinides from \[Th(90)\] to \[Lr(103)\]
Each series consists of 14 elements i.e. in the lanthanides, \[4f\]is gradually filled up while in actinides, \[5f\]is gradually filled up.
The properties of these elements are similar to transition elements. The members of actinide series are radioactive and majority of them are not found in nature. The elements from atomic number of 93 onwards are called transuranic elements and have been discovered artificial means.
In this classification the element, Zn, Cd and Hg have not been included in any of the four groups of elements. The elements Lu and Lr of the inner transition group have \[(n-2)\ f\]shell complete consisting 14 electron hence their inclusion in this group is not justified.
(1) Dobereiner's law of triads (1829) : It was the classification of elements into groups of three elements each with similar properties such that the atomic weight of the middle element was the arithmetic mean of the other two e.g. Ca, Sr, Ba, Cl, Br, I etc.
(2) Telluric screw or Helix (1862) : It was proposed by Chancourtois.
(3) Newlands law of octaves (1864) : It was an arrangement of elements in order of increasing atomic weights in which it was observed that every eighth element had properties similar to those of the first just like the eighth node of an octave of music.
(4) Mendeleef's period law (1869) : The first significant classification was given by Mendeleeff in the form of periodic table, commonly known as Mendeleeff's periodic table. His periodic table was based on periodic law, ''The physical and chemical properties of elements are periodic functions of their atomic weights.''
In Mendeleef's periodic table elements are arranged in order of their increasing atomic weights in such a way that elements with similar properties are placed in the same group. It consists of seven horizontal rows called periods. These are numbered from 1 to 7.
Mendeleef's original table consists of 8 vertical columns called groups. These are numbered as I, II III... VIII. However, 9th vertical column called Zero group was added with the discovery of inert gases. Except for group VIII and zero, each group is further divided into two sub-groups designated as A and B. Group VIII consists of 9 elements arranged in three sets each containing three elements.
(5) Modern Periodic Law : The recent work has established that the fundamental property of an atom is atomic number and not atomic weight. Therefore, atomic number is taken as the basis of the classification of the elements. The modern periodic law was given by Moseley, it may be stated as : ''The properties of elements are periodic functions of their atomic number".
When atomic number is taken as the basis for classification of elements, many anomalies of Mendeleef's table disappear, such as the,
(i) Position of hydrogen : Dual behaviour of hydrogen is explained on the fact that it has one electron in its outermost orbit. When it loses its electron it gives H+ and behaves like alkali metals and when it gains an electron it gives H– and behaves like halogens. Thus, it resembles with both the alkali metals and the halogens.
(ii) Dissimilar elements placed together : The lengths of periods are determined by the arrangement of electrons in different orbits. The period ends on the completion of last orbits (last members always being the inert gas). Different periods contain 2, 8, 18 or 32 elements. Now out of the two elements which every long period adds to the group, one resembles the typical elements while the other does not. This gives rise to formation of subgroups. This explains the inclusion of dissimilar elements in the same group but different subgroups.
(iii) Position of rare more...
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |
