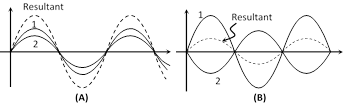
 \[BC=AD\]
and \[\angle i=\angle r\]
Refraction
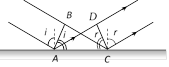
\[BC=AD\]
and \[\angle i=\angle r\]
Refraction
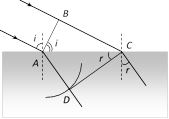 \[\frac{BC}{AD}=\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{\sin i}{\sin r}=\frac{{{\mu }_{2}}}{{{\mu }_{1}}}\]
\[\frac{BC}{AD}=\frac{{{v}_{1}}}{{{v}_{2}}}=\frac{\sin i}{\sin r}=\frac{{{\mu }_{2}}}{{{\mu }_{1}}}\] 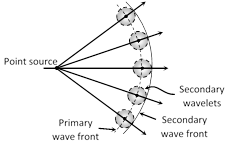 Different types of wavefront
Different types of wavefront
| Type of wavefront | Intensity | Amplitude |
Spherical
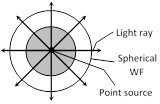
|
\[I\propto \frac{1}{{{r}^{2}}}\] | \[A\propto \frac{1}{r}\] |
Cylindrical
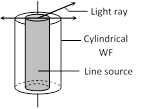
|
\[I\propto \frac{1}{r}\] | \[A\propto \frac{1}{\sqrt{r}}\] |
Plane
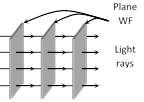
|
\[I\propto {{r}^{0}}\] | \[A\propto {{r}^{0}}\] |
| Light source | Flux (lumen) | Efficiency (lumen/watt) |
| 40 W tungsten bulb 60 W tungsten bulb 500 W tungsten bulb 30 W fluorescent tube | 465 835 9950 1500 | 12 14 20 50 |
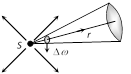 (i) more...
(i) more...  \[R.L.=\frac{\lambda }{2\mu \sin \theta }\] and\[R.P.=\frac{2\mu \sin \theta }{\lambda }\Rightarrow \]\[R.P.\propto \frac{1}{\lambda }\]
\[\lambda =\] Wavelength of light used to illuminate the object,
\[\mu =\] Refractive index of the medium between object and objective,
\[\theta =\] Half angle of the cone of light from the point object, \[\mu \sin \theta \]= Numerical aperture.
(2) Telescope : Smallest angular separations \[(d\theta )\] between two distant objects, whose images are separated in the telescope is called resolving limit. So resolving limit \[d\theta =\frac{1.22\lambda }{a}\]
and resolving power \[(RP)=\frac{1}{d\theta }=\frac{a}{1.22\lambda }\Rightarrow \]\[R.P.\propto \frac{1}{\lambda }\] where a = aperture of objective.
\[R.L.=\frac{\lambda }{2\mu \sin \theta }\] and\[R.P.=\frac{2\mu \sin \theta }{\lambda }\Rightarrow \]\[R.P.\propto \frac{1}{\lambda }\]
\[\lambda =\] Wavelength of light used to illuminate the object,
\[\mu =\] Refractive index of the medium between object and objective,
\[\theta =\] Half angle of the cone of light from the point object, \[\mu \sin \theta \]= Numerical aperture.
(2) Telescope : Smallest angular separations \[(d\theta )\] between two distant objects, whose images are separated in the telescope is called resolving limit. So resolving limit \[d\theta =\frac{1.22\lambda }{a}\]
and resolving power \[(RP)=\frac{1}{d\theta }=\frac{a}{1.22\lambda }\Rightarrow \]\[R.P.\propto \frac{1}{\lambda }\] where a = aperture of objective. 
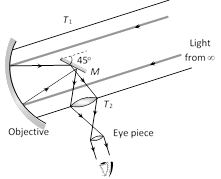 If \[{{f}_{o}}\] is focal length of the concave spherical mirror used as objective and \[{{f}_{e}},\] the focal length of the eye-piece, the magnifying power of the reflecting telescope is given by \[m=\frac{{{f}_{o}}}{{{f}_{e}}}\]
Further, if D is diameter of the objective and d, the diameter of the pupil of the eye, then brightness ratio \[(\beta )\] is given by \[\beta =\frac{{{D}^{2}}}{{{d}^{2}}}\]
If \[{{f}_{o}}\] is focal length of the concave spherical mirror used as objective and \[{{f}_{e}},\] the focal length of the eye-piece, the magnifying power of the reflecting telescope is given by \[m=\frac{{{f}_{o}}}{{{f}_{e}}}\]
Further, if D is diameter of the objective and d, the diameter of the pupil of the eye, then brightness ratio \[(\beta )\] is given by \[\beta =\frac{{{D}^{2}}}{{{d}^{2}}}\]  (1) Objective is a converging lens while eye lens is diverging lens.
(2) Magnification : \[{{m}_{D}}=\frac{{{f}_{0}}}{{{f}_{e}}}\left( 1-\frac{{{f}_{e}}}{D} \right)\] and \[{{m}_{\infty }}=\frac{{{f}_{0}}}{{{f}_{e}}}\]
(3) Length : \[{{L}_{D}}={{f}_{0}}-{{u}_{e}}\] and \[{{L}_{\infty }}={{f}_{0}}-{{f}_{e}}\]
(1) Objective is a converging lens while eye lens is diverging lens.
(2) Magnification : \[{{m}_{D}}=\frac{{{f}_{0}}}{{{f}_{e}}}\left( 1-\frac{{{f}_{e}}}{D} \right)\] and \[{{m}_{\infty }}=\frac{{{f}_{0}}}{{{f}_{e}}}\]
(3) Length : \[{{L}_{D}}={{f}_{0}}-{{u}_{e}}\] and \[{{L}_{\infty }}={{f}_{0}}-{{f}_{e}}\] You need to login to perform this action.
You will be redirected in
3 sec
