question_answer 1)
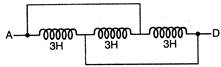
The inductance between A and D is:
A)
3.66 H
done
clear
B)
9 H
done
clear
C)
0.66 H
done
clear
D)
1 H
done
clear
View Answer play_arrow
question_answer 2) A ball whose kinetic energy is E, is projected at an angle of\[45{}^\circ \]to the horizontal. The kinetic energy of the ball at the highest point of its flight will be:
A)
E
done
clear
B)
\[E/\sqrt{2}\]
done
clear
C)
E/2
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 3) From a building two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically). If\[{{v}_{A}}\]and\[{{v}_{B}}\]are their respective velocities on reaching the ground, then
A)
\[{{v}_{B}}>{{v}_{A}}\]
done
clear
B)
\[{{v}_{A}}={{v}_{B}}\]
done
clear
C)
\[{{v}_{A}}>{{v}_{B}}\]
done
clear
D)
their velocities depends on their masses
done
clear
View Answer play_arrow
question_answer 4) If a body loses half of its velocity on penetrating 3cm in a wooden block, then how much will it penetrate more before coming to rest?
A)
1 cm
done
clear
B)
2 cm
done
clear
C)
3 cm
done
clear
D)
4 cm
done
clear
View Answer play_arrow
question_answer 5) If suddenly the gravitational force of attraction between earth and a satellite revolving around it becomes zero, then the satellite will:
A)
continue to move in its orbit with same velocity
done
clear
B)
move tangentially to the original orbit with the same velocity
done
clear
C)
become stationary in its orbit
done
clear
D)
move towards the earth
done
clear
View Answer play_arrow
question_answer 6) If an ammeter is to be used in place of a voltmeter, then we must connect with the ammeter a:
A)
low resistance in parallel
done
clear
B)
high resistance in parallel
done
clear
C)
high resistance in series
done
clear
D)
low resistance in series
done
clear
View Answer play_arrow
question_answer 7) If in a circular coil A of radius R, current\[i\]is flowing and in another coil B of radius 2R a current\[2i\]is flowing, then the ratio of the magnetic fields,\[{{B}_{A}}\]and\[{{B}_{B}}\]produced by them will be:
A)
1
done
clear
B)
2
done
clear
C)
1/2
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 8) If two mirrors are kept at\[60{}^\circ \]to each other, then the number of images formed by them is:
A)
5
done
clear
B)
6
done
clear
C)
7
done
clear
D)
8
done
clear
View Answer play_arrow
question_answer 9) A wire when connected to 220V mains supply has power dissipation\[{{P}_{1}}\]. Now the wire is cut into two equal pieces which are connected in parallel to the same supply. Power dissipation in this case is\[{{P}_{2}}\]. Then\[{{P}_{2}}:{{P}_{1}}\]is
A)
1
done
clear
B)
4
done
clear
C)
2
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 10) If 13.6eV energy is required to ionize the hydrogen atom, then the energy required to remove an electron from\[n=2\]is:
A)
10.2 eV
done
clear
B)
0 eV
done
clear
C)
3.4 eV
done
clear
D)
6.8 eV
done
clear
View Answer play_arrow
question_answer 11) Tube A has both ends open while tube B has one end closed, otherwise they are identical. The ratio of fundamental frequency of tubes A and B is:
A)
\[1:2\]
done
clear
B)
\[1:4\]
done
clear
C)
\[2:1\]
done
clear
D)
\[4:1\]
done
clear
View Answer play_arrow
question_answer 12) A tuning fork arrangement (pair) produces 4 beats/sec with one fork of frequency 288 .cps. A little wax is placed on the unknown fork and it then produces 2 beats/sec. The frequency of the unknown folk is:
A)
286 cps
done
clear
B)
292 cps
done
clear
C)
294 cps
done
clear
D)
288 cps
done
clear
View Answer play_arrow
question_answer 13) A wave\[y=a\sin (\omega t-kx)\]on a string meets with another wave producing a node at\[x=0\]. Then the equation of the unknown wave is:
A)
\[y=a\sin (\omega t+kx)\]
done
clear
B)
\[y=-a\sin (\omega t+kx)\]
done
clear
C)
\[y=a\sin (\omega t-kx)\]
done
clear
D)
\[y=-a\sin (\omega t-kx)\]
done
clear
View Answer play_arrow
question_answer 14) On moving a charge of 20 coulombs by 2 cm, 2 J of work is done, then the potential difference between the points is:
A)
0.1 V
done
clear
B)
8 V
done
clear
C)
2 V
done
clear
D)
0.5 V
done
clear
View Answer play_arrow
question_answer 15) If an electron and a proton having same momenta enter perpendicularly to a magnetic field, then:
A)
curved path of electron and proton will be same (ignoring the sense of revolution)
done
clear
B)
they will move under flecked
done
clear
C)
curved path of electron is more curved than that of proton
done
clear
D)
path of proton is more curved
done
clear
View Answer play_arrow
question_answer 16) Energy required to move a body of mass m from an orbit of radius 2R to 3R is:
A)
\[GMm/12{{R}^{2}}\]
done
clear
B)
\[GMm/3{{R}^{2}}\]
done
clear
C)
\[GMm/8R\]
done
clear
D)
\[GMm/6R\]
done
clear
View Answer play_arrow
question_answer 17) If a spring has time period T, and is cut into n equal parts, then the time period of each part will be:
A)
\[T\sqrt{n}\]
done
clear
B)
\[T/\sqrt{n}\]
done
clear
C)
\[nT\]
done
clear
D)
\[T\]
done
clear
View Answer play_arrow
question_answer 18)
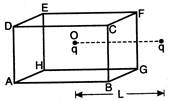
A charged particle q is placed at the centre\[O\] of cube of length L (ABCDEFGH). Another same charge q is placed at a distance L from Then the electrons flux through ABCD is:
A)
\[q/4\pi {{\varepsilon }_{0}}L\]
done
clear
B)
zero
done
clear
C)
\[q/2\pi {{\varepsilon }_{0}}L\]
done
clear
D)
\[q/3\pi {{\varepsilon }_{0}}L\]
done
clear
View Answer play_arrow
question_answer 19)
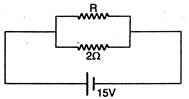
If in the circuit, power dissipation is 150 W, then R is:
A)
\[2\,\Omega \]
done
clear
B)
\[6\,\Omega \]
done
clear
C)
\[5\,\Omega \]
done
clear
D)
\[4\,\Omega \]
done
clear
View Answer play_arrow
question_answer 20) Wavelength of light used in an optical instrument are\[{{\lambda }_{1}}=4000\,\overset{o}{\mathop{\text{A}}}\,\]and\[{{\lambda }_{2}}=5000\,\overset{o}{\mathop{\text{A}}}\,,\]then ratio of their respective resolving powers (corresponding to\[{{\lambda }_{1}}\]and\[{{\lambda }_{2}}\]) is:
A)
\[16:25\]
done
clear
B)
\[9:1\]
done
clear
C)
\[4:5\]
done
clear
D)
\[5:4\]
done
clear
View Answer play_arrow
question_answer 21) Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
A)
v
done
clear
B)
v/3
done
clear
C)
v/2
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 22) If a current is passed through a spring then the spring will:
A)
expand
done
clear
B)
compress
done
clear
C)
remain same
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 23) Heat given to a body which raises its temperature by\[1{}^\circ C\]is:
A)
water equivalent
done
clear
B)
thermal capacity
done
clear
C)
specific heat
done
clear
D)
temperature gradient
done
clear
View Answer play_arrow
question_answer 24) At absolute zero, Si acts as:
A)
non-metal
done
clear
B)
metal
done
clear
C)
insulator
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 25) Electromagnetic waves are transverse in nature is evident by:
A)
polarization
done
clear
B)
interference
done
clear
C)
reflection
done
clear
D)
diffraction
done
clear
View Answer play_arrow
question_answer 26) Which of the following is used in optical fibres?
A)
Total internal reflection
done
clear
B)
Scattering
done
clear
C)
Diffraction
done
clear
D)
Refraction
done
clear
View Answer play_arrow
question_answer 27) The escape velocity of a body depends upon mass as:
A)
\[{{m}^{0}}\]
done
clear
B)
\[{{m}^{1}}\]
done
clear
C)
\[{{m}^{2}}\]
done
clear
D)
\[{{m}^{3}}\]
done
clear
View Answer play_arrow
question_answer 28) Which of the following are not electro- magnetic waves?
A)
Cosmic-rays
done
clear
B)
y rays
done
clear
C)
\[\beta -rays\]
done
clear
D)
X-rays
done
clear
View Answer play_arrow
question_answer 29) Identify the pair whose dimensions are equal:
A)
torque and work
done
clear
B)
stress and energy
done
clear
C)
force and stress
done
clear
D)
force and work
done
clear
View Answer play_arrow
question_answer 30) If\[{{\theta }_{i}}\] is the inversion temperature,\[{{\theta }_{n}}\]is the neutral temperature,\[{{\theta }_{c}}\]. is the temperature of the cold junction then:
A)
\[{{\theta }_{i}}+{{\theta }_{c}}={{\theta }_{n}}\]
done
clear
B)
\[{{\theta }_{i}}-{{\theta }_{c}}=2{{\theta }_{n}}\]
done
clear
C)
\[\frac{{{\theta }_{i}}-{{\theta }_{c}}}{2}={{\theta }_{n}}\]
done
clear
D)
\[{{\theta }_{c}}-{{\theta }_{i}}=2{{\theta }_{n}}\]
done
clear
View Answer play_arrow
question_answer 31) Infrared radiations are detected by:
A)
spectrometer
done
clear
B)
pyrometer
done
clear
C)
nanometer
done
clear
D)
photometer
done
clear
View Answer play_arrow
question_answer 32) If\[{{N}_{0}}\]is the original mass of the substance of half-life period\[{{t}_{1/2}}=5\]years, then the amount of substance left after 15 years is:
A)
\[{{N}_{0}}/8\]
done
clear
B)
\[{{N}_{0}}/16\]
done
clear
C)
\[{{N}_{0}}/2\]
done
clear
D)
\[{{N}_{0}}/4\]
done
clear
View Answer play_arrow
question_answer 33) By increasing the temperature, the specific resistance of a conductor and a semiconductor:
A)
increases for both
done
clear
B)
decreases for both
done
clear
C)
increases, decreases respectively
done
clear
D)
decreases, increases respectively
done
clear
View Answer play_arrow
question_answer 34) If there are n capacitors in parallel connected to V volt source, then the energy stored is equal to:
A)
\[CV\]
done
clear
B)
\[\frac{1}{2}nC{{V}^{2}}\]
done
clear
C)
\[C{{V}^{2}}\]
done
clear
D)
\[\frac{1}{2n}C{{V}^{2}}\]
done
clear
View Answer play_arrow
question_answer 35) Which of the following is more close to a black body?
A)
Black board paint
done
clear
B)
Green leaves
done
clear
C)
Black holes
done
clear
D)
Red roses
done
clear
View Answer play_arrow
question_answer 36) Which statement is incorrect?
A)
All reversible cycles have same efficiency
done
clear
B)
Reversible cycle has more efficiency than an irreversible one
done
clear
C)
Carnot cycle is a reversible one
done
clear
D)
Carnot cycle has the maximum efficiency in all cycles
done
clear
View Answer play_arrow
question_answer 37) Length of a string tied to two rigid supports is 40cm. Maximum length (wavelength in cm) of a stationary wave produced on it, is:
A)
20
done
clear
B)
80
done
clear
C)
40
done
clear
D)
120
done
clear
View Answer play_arrow
question_answer 38) The power factor of an A.C. circuit having resistance R and inductance L (connected in series) and an angular velocity\[\omega \]is:
A)
\[R/\omega L\]
done
clear
B)
\[R{{({{R}^{2}}+{{\omega }^{2}}{{L}^{2}})}^{1/2}}\]
done
clear
C)
\[\omega L/R\]
done
clear
D)
\[R/{{({{R}^{2}}-{{\omega }^{2}}{{L}^{2}})}^{1/2}}\]
done
clear
View Answer play_arrow
question_answer 39) An astronomical telescope has a large aperture to:
A)
reduce spherical aberration
done
clear
B)
have high resolution
done
clear
C)
increase span of observation
done
clear
D)
have low dispersion
done
clear
View Answer play_arrow
question_answer 40) The kinetic energy needed to project a body of mass m from the earths surface (radius R) to infinity is:
A)
\[mgR/2\]
done
clear
B)
\[2mgR\]
done
clear
C)
\[mgR\]
done
clear
D)
\[mgR/4\]
done
clear
View Answer play_arrow
question_answer 41) Cooking gas containers are kept in a lorry moving with uniform speed. The temperature of the gas molecules inside will:
A)
increase
done
clear
B)
decrease
done
clear
C)
remain same
done
clear
D)
decrease for some, while increase for others
done
clear
View Answer play_arrow
question_answer 42) When temperature increases, the frequency of a tuning fork:
A)
increases
done
clear
B)
decreases
done
clear
C)
remains same
done
clear
D)
increases or decreases depending on the material
done
clear
View Answer play_arrow
question_answer 43) If mass-energy equivalence is taken into account, when water is cooled to form ice, the mass of water should:
A)
increase
done
clear
B)
remain unchanged
done
clear
C)
decrease
done
clear
D)
first increase then decrease
done
clear
View Answer play_arrow
question_answer 44) The energy band gap is maximum in:
A)
metals
done
clear
B)
superconductors
done
clear
C)
insulators
done
clear
D)
semiconductors
done
clear
View Answer play_arrow
question_answer 45) The part of a transistor which is most heavily doped to produce large number of majority carriers is:
A)
emitter
done
clear
B)
base
done
clear
C)
collector
done
clear
D)
can be any of the above three
done
clear
View Answer play_arrow
question_answer 46) In a simple harmonic oscillator, at the mean position:
A)
kinetic energy is minimum, potential energy is maximum
done
clear
B)
both kinetic and potential energies are maximum
done
clear
C)
kinetic energy is maximum, potential energy is minimum
done
clear
D)
both kinetic and potential energies are minimum
done
clear
View Answer play_arrow
question_answer 47) Initial angular velocity of a circular disc of mass M is\[{{\omega }_{1}}\]. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc?
A)
\[\left( \frac{M+m}{M} \right){{\omega }_{1}}\]
done
clear
B)
\[\left( \frac{M+m}{m} \right){{\omega }_{1}}\]
done
clear
C)
\[\left( \frac{M}{M+4m} \right){{\omega }_{1}}\]
done
clear
D)
\[\left( \frac{M}{M+2m} \right){{\omega }_{1}}\]
done
clear
View Answer play_arrow
question_answer 48) The minimum velocity (in\[m{{s}^{-1}}\]) with which a car driver must traverse a flat curve of radius 150m and coefficient of friction 0.6 to avoid skidding is:
A)
60
done
clear
B)
30
done
clear
C)
15
done
clear
D)
25
done
clear
View Answer play_arrow
question_answer 49) A cylinder of height 20 m is completely filled with water. The velocity of efflux of water (in \[m{{s}^{-1}}\]) through a small hole on the side wall of the cylinder near its bottom, is:
A)
10
done
clear
B)
20
done
clear
C)
25.5
done
clear
D)
5
done
clear
View Answer play_arrow
question_answer 50) A spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
A)
16 J
done
clear
B)
8 J
done
clear
C)
32 J
done
clear
D)
24 J
done
clear
View Answer play_arrow
question_answer 51) A child swinging on a swing in sitting position, stands up, then the time period of the swing will:
A)
increase
done
clear
B)
decrease
done
clear
C)
remain same
done
clear
D)
increase if the child is long and decrease if the child is short
done
clear
View Answer play_arrow
question_answer 52) A lift is moving down with acceleration a. Aman in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively:
A)
\[g,g\]
done
clear
B)
\[g-a.\text{ }g-a\]
done
clear
C)
\[g-a,g\]
done
clear
D)
\[a,g\]
done
clear
View Answer play_arrow
question_answer 53) The mass of a product liberated on anode in an electrochemical cell depends on:
A)
\[{{(It)}^{1/2}}\]
done
clear
B)
\[It\]
done
clear
C)
\[I/t\]
done
clear
D)
\[{{I}^{2}}t\]
done
clear
View Answer play_arrow
question_answer 54) At what temperature is the rms velocity of a hydrogen molecule equal to that of an oxygen molecule at\[47{}^\circ C\]?
A)
80 K
done
clear
B)
\[-73\text{ }K\]
done
clear
C)
3 K
done
clear
D)
20 K
done
clear
View Answer play_arrow
question_answer 55) The time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its:
A)
speed
done
clear
B)
mass
done
clear
C)
charge
done
clear
D)
magnetic induction
done
clear
View Answer play_arrow
question_answer 56) Which of the following is a redox reaction?
A)
\[NaCl+KN{{O}_{3}}\xrightarrow[{}]{{}}NaN{{O}_{3}}+KCl\]
done
clear
B)
\[Ca{{C}_{2}}{{O}_{4}}+2HCl\xrightarrow[{}]{{}}CaC{{l}_{2}}+{{H}_{2}}{{C}_{2}}{{O}_{4}}\]
done
clear
C)
\[Ca{{(OH)}_{2}}+2N{{H}_{4}}Cl\xrightarrow[{}]{{}}\]\[CaC{{l}_{2}}+2N{{H}_{3}}+2{{H}_{2}}O\]
done
clear
D)
\[2K[Ag{{(CN)}_{2}}]+Zn\xrightarrow[{}]{{}}\] \[2Ag+{{K}_{2}}[Zn{{(CN)}_{4}}]\]
done
clear
View Answer play_arrow
question_answer 57) For an ideal gas, number of mol per litre in terms of its pressure P, temperature T and gas constant R is:
A)
PT/R
done
clear
B)
PRT
done
clear
C)
P/RT
done
clear
D)
RT/P
done
clear
View Answer play_arrow
question_answer 58) Number of\[P-O\]bonds in\[{{P}_{4}}{{O}_{10}}\]is:
A)
17
done
clear
B)
16
done
clear
C)
15
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 59) \[K{{O}_{2}}\]is used in space and submarines because it:
A)
absorbs\[C{{O}_{2}}\]and increases\[{{O}_{2}}\]concentration
done
clear
B)
absorbs moisture
done
clear
C)
absorbs\[C{{O}_{2}}\]
done
clear
D)
produces ozone
done
clear
View Answer play_arrow
question_answer 60) Which of the following ions has the maximum magnetic moment?
A)
\[M{{n}^{2+}}\]
done
clear
B)
\[F{{e}^{2+}}\]
done
clear
C)
\[T{{i}^{2+}}\]
done
clear
D)
\[C{{r}^{2+}}\]
done
clear
View Answer play_arrow
question_answer 61) Acetylene does not react with:
A)
Na
done
clear
B)
ammonical\[AgN{{O}_{3}}\]
done
clear
C)
\[HCl\]
done
clear
D)
\[NaOH\]
done
clear
View Answer play_arrow
question_answer 62)
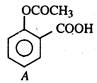
Compound A given below is:
A)
antiseptic
done
clear
B)
antibiotic
done
clear
C)
analgesic
done
clear
D)
pesticide
done
clear
View Answer play_arrow
question_answer 63) For the following cell with hydrogen electrodes at two different pressures\[{{p}_{1}}\]and\[{{p}_{2}}\]\[\underset{{{p}_{1}}}{\mathop{pt({{H}_{2}})}}\,|\underset{1\,M}{\mathop{{{H}^{+}}(aq).}}\,|\underset{{{p}_{2}}}{\mathop{Pt({{H}_{2}})}}\,\]emf is given by:
A)
\[\frac{RT}{F}{{\log }_{e}}\frac{{{p}_{1}}}{{{p}_{2}}}\]
done
clear
B)
\[\frac{RT}{2F}{{\log }_{e}}\frac{{{p}_{1}}}{{{p}_{2}}}\]
done
clear
C)
\[\frac{RT}{F}{{\log }_{e}}\frac{{{p}_{2}}}{{{p}_{1}}}\]
done
clear
D)
\[\frac{RT}{2F}{{\log }_{e}}\frac{{{p}_{2}}}{{{p}_{1}}}\]
done
clear
View Answer play_arrow
question_answer 64) Acetylene reacts with hypochlorous acid to form:
A)
\[C{{l}_{2}}CHCHO\]
done
clear
B)
\[ClC{{H}_{2}}COOH\]
done
clear
C)
\[C{{H}_{3}}COCl\]
done
clear
D)
\[ClC{{H}_{2}}CHO\]
done
clear
View Answer play_arrow
question_answer 65) On heating benzyl amine with chloroform and ethanolic KOH, product obtained is:
A)
benzyl alcohol
done
clear
B)
benzaldehyde
done
clear
C)
benzonitrile
done
clear
D)
benzyl isocyanide
done
clear
View Answer play_arrow
question_answer 66) Which of the following reaction is possible at anode?
A)
\[{{F}_{2}}+2{{e}^{-}}\xrightarrow[{}]{{}}2{{F}^{-}}\]
done
clear
B)
\[2{{H}^{+}}+\frac{1}{2}{{O}_{2}}+2{{e}^{-}}\xrightarrow[{}]{{}}{{H}_{2}}O\]
done
clear
C)
\[2Cr_{2}^{3+}+7{{H}_{2}}O\xrightarrow[{}]{{}}C{{r}_{2}}O_{7}^{2-}+14{{H}^{+}}+6{{e}^{-}}\]
done
clear
D)
\[F{{e}^{2+}}\xrightarrow[{}]{{}}F{{e}^{3+}}+{{e}^{-}}\]
done
clear
View Answer play_arrow
question_answer 67) Which of the following concentration factor is affected by change in temperature?
A)
Molarity
done
clear
B)
Molality
done
clear
C)
Mol fraction
done
clear
D)
Weight fraction
done
clear
View Answer play_arrow
question_answer 68) Cyanide process is used for the extraction of:
A)
barium
done
clear
B)
silver
done
clear
C)
boron
done
clear
D)
zinc
done
clear
View Answer play_arrow
question_answer 69) Following reaction\[{{(C{{H}_{3}})}_{3}}CBr+{{H}_{2}}O\xrightarrow[{}]{{}}{{(C{{H}_{3}})}_{3}}COH+HBr\]is an example of:
A)
elimination reaction
done
clear
B)
free radical substitution
done
clear
C)
nucleophilic substitution
done
clear
D)
electrophilic substitution
done
clear
View Answer play_arrow
question_answer 70) A metal M forms water soluble\[MS{{O}_{4}}\] and inert \[MO.\text{ }MO\]in aqueous solution forms insoluble \[M{{(OH)}_{2}}\]soluble in\[NaOH\]. Metal M is:
A)
Be
done
clear
B)
Mg
done
clear
C)
Ca
done
clear
D)
Si
done
clear
View Answer play_arrow
question_answer 71) Half life of a substance A following first order kinetics is 5 days. Starting with 100 g of A, amount left after 15 days is:
A)
25 g
done
clear
B)
50 g
done
clear
C)
12.5 g
done
clear
D)
6.25 g
done
clear
View Answer play_arrow
question_answer 72) The most stable ion is:
A)
\[{{[Fe{{(OH)}_{5}}]}^{3-}}\]
done
clear
B)
\[{{[FeC{{l}_{6}}]}^{3-}}\]
done
clear
C)
\[{{[Fe{{(CN)}_{6}}]}^{3-}}\]
done
clear
D)
\[{{[Fe{{({{H}_{2}}O)}_{6}}]}^{3+}}\]
done
clear
View Answer play_arrow
question_answer 73) A substance forms zwitter ion. It can have functional groups:
A)
\[-N{{H}_{2}},-COOH\]
done
clear
B)
\[-N{{H}_{2}},-S{{O}_{3}}H\]
done
clear
C)
both (a) and (b)
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 74) If\[F{{e}^{3+}}\]and\[C{{r}^{3+}}\]both are present in group III of qualitative analysis, then distinction can be made by:
A)
addition of\[N{{H}_{4}}OH\]in presence of\[N{{H}_{4}}Cl\]when only\[Fe{{(OH)}_{3}}\]is precipitated
done
clear
B)
addition of\[N{{H}_{4}}OH\]in presence of\[N{{H}_{4}}Cl\]when\[Cr{{(OH)}_{3}}\]and\[Fe{{(OH)}_{3}}\]both are precipitated and on adding\[B{{r}_{2}}\]water and \[NaOH,Cr{{(OH)}_{3}}\]dissolves
done
clear
C)
precipitate of\[Cr{{(OH)}_{3}}\]and\[Fe{{(OH)}_{3}}\]as obtained in are treated! with cone.\[HCl\] when only\[Fe{{(OH)}_{3}}\]dissolves
done
clear
D)
and (b) the (c) correct.
done
clear
View Answer play_arrow
question_answer 75) In an organic compound of molar mass 108 g \[mo{{l}^{-1}}C,H\] and N atoms are present in \[9:1:3.5\]by weight. Molecular formula can be:
A)
\[{{C}_{6}}{{H}_{8}}{{N}_{2}}\]
done
clear
B)
\[{{C}_{7}}{{H}_{10}}N\]
done
clear
C)
\[{{C}_{5}}{{H}_{6}}{{N}_{3}}\]
done
clear
D)
\[{{C}_{4}}{{H}_{18}}{{N}_{3}}\]
done
clear
View Answer play_arrow
question_answer 76) Solubility of\[Ca{{(OH)}_{2}}\]is\[S\text{ }mol\text{ }litr{{e}^{-1}}\]. The solubility product\[({{K}_{sp}})\]under the same condition is:
A)
\[4{{S}^{3}}\]
done
clear
B)
\[3{{S}^{4}}\]
done
clear
C)
\[4{{S}^{2}}\]
done
clear
D)
\[{{S}^{3}}\]
done
clear
View Answer play_arrow
question_answer 77) Heat required to raise the temperature of 1 mol of a substance by\[1{}^\circ \]is called:
A)
specific heat
done
clear
B)
molar heat capacity
done
clear
C)
water equivalent
done
clear
D)
specific gravity
done
clear
View Answer play_arrow
question_answer 78) \[\beta -\]particle is emitted in a radioactive reaction when:
A)
a proton changes to neutron
done
clear
B)
a neutron changes to proton
done
clear
C)
a neutron changes to electron
done
clear
D)
an electron changes to neutron
done
clear
View Answer play_arrow
question_answer 79) In a mixture of A and B, components show negative deviation when:
A)
\[A-B\] interaction is stronger than\[A-A\] and\[B-B\]interaction
done
clear
B)
\[A-B\]interaction is weaker than\[A-A\]and \[B-B\]interaction
done
clear
C)
\[\Delta {{V}_{mix}}>0,\Delta {{S}_{mix}}>0\]
done
clear
D)
\[\Delta {{V}_{mix}}=0,\Delta {{S}_{mix}}>0\]
done
clear
View Answer play_arrow
question_answer 80) Refining of impure copper with zinc impurity is to be done by electrolysis using electrons as: Cathode Anode
A)
pure copper pure zinc
done
clear
B)
pure zinc pure copper
done
clear
C)
pure copper impure copper
done
clear
D)
pure zinc impure zinc
done
clear
View Answer play_arrow
question_answer 81) Aluminium is extracted by the electrolysis of:
A)
alumina
done
clear
B)
bauxite
done
clear
C)
molten cryolite
done
clear
D)
alumina mixed with molten cryolite
done
clear
View Answer play_arrow
question_answer 82) For an aqueous solution, freezing point is\[-0.186{}^\circ C\]. Elevation of the boiling point of the same solution is (\[{{K}_{f}}=1.86{}^\circ mo{{l}^{-1}}kg\]and \[{{K}_{f}}=0.512{}^\circ mo{{l}^{-1}}kg\]):
A)
\[0.186{}^\circ \]
done
clear
B)
\[0.0512{}^\circ \]
done
clear
C)
\[1.86{}^\circ \]
done
clear
D)
\[5.12{}^\circ \]
done
clear
View Answer play_arrow
question_answer 83) Underlined carbon is\[s{{p}^{3}}\]hybridised in:
A)
\[C{{H}_{3}}\underline{C}H=C{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}\underline{C}{{H}_{2}}N{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}\underline{C}ON{{H}_{2}}\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}\underline{C}N\]
done
clear
View Answer play_arrow
question_answer 84) Bond angle of\[109{}^\circ 28\]is found in:
A)
\[N{{H}_{3}}\]
done
clear
B)
\[{{H}_{2}}O\]
done
clear
C)
\[C{{H}_{5}}\]
done
clear
D)
\[N{{H}_{4}}\]
done
clear
View Answer play_arrow
question_answer 85) For a reaction\[A+2B\xrightarrow[{}]{{}}C,\]rate is given by \[+\frac{d[C]}{dt}=k[A][B],\]hence the order of the reaction is:
A)
3
done
clear
B)
2
done
clear
C)
1
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 86) \[C{{H}_{3}}MgI\]is an organometallic compound due to:
A)
\[Mg-I\]bond
done
clear
B)
\[C-I\]bond
done
clear
C)
\[C-Mg\]bond
done
clear
D)
\[C-H\]bond
done
clear
View Answer play_arrow
question_answer 87) One of the following species acts as both Bronsted acid and base:
A)
\[{{H}_{2}}PO_{2}^{-}\]
done
clear
B)
\[HPO_{3}^{2-}\]
done
clear
C)
\[HPO_{4}^{2-}\]
done
clear
D)
all of the above
done
clear
View Answer play_arrow
question_answer 88) Hybridisation of the underline atom changes in:
A)
\[\underline{A}l{{H}_{3}}\]changes to\[AlH_{4}^{-}\]
done
clear
B)
\[{{H}_{2}}\underline{O}\]changes to\[{{H}_{3}}{{O}^{+}}\]
done
clear
C)
\[\underline{N}{{H}_{3}}\]changes to\[NH_{4}^{+}\]
done
clear
D)
in all cases
done
clear
View Answer play_arrow
question_answer 89) Racemic mixture is formed by mixing two:
A)
isomeric compounds
done
clear
B)
chiral compounds
done
clear
C)
meso compounds
done
clear
D)
enantiomers with chiral carbon
done
clear
View Answer play_arrow
question_answer 90) The number of lone pairs on\[Xe\]in\[Xe{{F}_{2}},\]\[Xe{{F}_{4}}\] and\[Xe{{F}_{6}}\]respectively are:
A)
3, 2, 1
done
clear
B)
2, 4, 6
done
clear
C)
1, 2, 3
done
clear
D)
6, 4, 2
done
clear
View Answer play_arrow
question_answer 91) An aqueous solution of\[1\,M\,NaCl\]and\[1M\text{ }HCl\]is:
A)
not a buffer but\[pH<7\]
done
clear
B)
not a buffer but\[pH>7\]
done
clear
C)
a buffer with\[pH<7\]
done
clear
D)
a buffer with\[pH>7\]
done
clear
View Answer play_arrow
question_answer 92) Consider following two reactions\[A\xrightarrow[{}]{{}}Product-\frac{d[A]}{dt}={{k}_{1}}{{[A]}^{0}}\]\[B\xrightarrow[{}]{{}}Product-\frac{d[B]}{dt}={{k}_{2}}[B]\]]\[{{k}_{1}}\]and\[{{k}_{2}}\] are expressed in terms of molarity\[(mol\text{ }{{L}^{-1}})\]and time\[(se{{c}^{-1}})\]as:
A)
\[se{{c}^{-1}},M\,{{\sec }^{-1}}{{L}^{-1}}\]
done
clear
B)
\[M\,se{{c}^{-1}},M\,{{\sec }^{-1}}\]
done
clear
C)
\[se{{c}^{-1}},{{M}^{-1}}\,{{\sec }^{-1}}\]
done
clear
D)
\[M\,se{{c}^{-1}},{{L}^{-1}}\,{{\sec }^{-1}}\]
done
clear
View Answer play_arrow
question_answer 93) RNA contains:
A)
ribose sugar and thymine
done
clear
B)
ribose sugar and uracil
done
clear
C)
deoxyribose sugar and uracil
done
clear
D)
deoxyribose sugar and thymine
done
clear
View Answer play_arrow
question_answer 94) For a cell given below: \[\underset{-}{\mathop{Ag|A{{g}^{+}}}}\,||\underset{+}{\mathop{C{{u}^{2+}}|Cu}}\,\]\[A{{g}^{+}}+{{e}^{-}}\xrightarrow[{}]{{}}Ag\] \[E{}^\circ =x\]\[C{{u}^{2+}}+2{{e}^{-}}\xrightarrow[{}]{{}}Cu,\] \[E{}^\circ =y\]E° cell is:
A)
\[x+2y\]
done
clear
B)
\[2x+y\]
done
clear
C)
\[y-x\]
done
clear
D)
\[y-2x\]
done
clear
View Answer play_arrow
question_answer 95) Based on kinetic theory of gases following laws can be proved:
A)
Boyles law
done
clear
B)
Charles law
done
clear
C)
Avogadros law
done
clear
D)
all of these
done
clear
View Answer play_arrow
question_answer 96) \[Mn{{O}_{4}}\]is a good oxidising agent in different medium changing to \[MnO_{4}^{-}\xrightarrow[{}]{{}}M{{n}^{2+}}\] \[\xrightarrow[{}]{{}}MnO_{4}^{2-}\] \[\xrightarrow[{}]{{}}Mn{{O}_{2}}\] \[\xrightarrow[{}]{{}}M{{n}_{2}}{{O}_{3}}\] Changes in oxidation number respectively are:
A)
1,3,4,5
done
clear
B)
5,4,3,2
done
clear
C)
5,1,3,4
done
clear
D)
2,6,4,3
done
clear
View Answer play_arrow
question_answer 97) For the reaction:\[{{H}_{2}}+{{I}_{2}}\xrightarrow[{}]{{}}2HI,\]the differential rate law is:
A)
\[-\frac{d[{{H}_{2}}]}{dt}=-\frac{d[{{I}_{2}}]}{dt}=2\frac{d[HI[}{dt}\]
done
clear
B)
\[-2\frac{d[{{H}_{2}}]}{dt}=-2\frac{d[{{I}_{2}}]}{dt}=\frac{d[HI]}{dt}\]
done
clear
C)
\[-\frac{d[{{H}_{2}}]}{dt}=-\frac{d[{{I}_{2}}]}{dt}=\frac{d[HI]}{dt}\]
done
clear
D)
\[-\frac{d[{{H}_{2}}]}{2dt}=-\frac{d[{{I}_{2}}]}{2dt}=\frac{d[HI]}{dt}\]
done
clear
View Answer play_arrow
question_answer 98) Number of atoms in 560 g of Fe (atomic mass\[56\text{ }g\text{ }mo{{l}^{-1}}\]) is:
A)
is twice that of 70 g N
done
clear
B)
is half that of 20 g H
done
clear
C)
both are correct
done
clear
D)
none is correct
done
clear
View Answer play_arrow
question_answer 99) Geometrical isomerism is not shown by:
A)
1, 1-dichloro-l-pentene
done
clear
B)
1, 2-dichloro-l-pentene
done
clear
C)
1, 3-dichloro-2-pentene
done
clear
D)
1, 4-dichloro-2-pentene
done
clear
View Answer play_arrow
question_answer 100) Number of atoms in the unit cell of Na (BCC type crystal) and Mg (FCC type crystal) are respectively:
A)
4, 4
done
clear
B)
4, 2
done
clear
C)
2, 4
done
clear
D)
1, 1
done
clear
View Answer play_arrow
question_answer 101) Which of the following compounds has incorrect IUPAC nomenclature?
A)
\[\underset{ethylbutanoate}{\mathop{C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}\overset{\begin{smallmatrix} O \\ |\,| \end{smallmatrix}}{\mathop{C}}\,O{{C}_{2}}{{H}_{5}}}}\,\]
done
clear
B)
\[\underset{3-methyl\text{ }butanal}{\mathop{C{{H}_{3}}\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{C}}\,C{{H}_{2}}CHO}}\,\]
done
clear
C)
\[\underset{2-methyl-3-pentanone}{\mathop{C{{H}_{3}}\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{CH\overset{\begin{smallmatrix} O \\ |\,| \end{smallmatrix}}{\mathop{C}}\,}}\,C{{H}_{2}}C{{H}_{3}}}}\,\]
done
clear
D)
\[\underset{2-methyl-3-butanol}{\mathop{C{{H}_{3}}\underset{\begin{smallmatrix} | \\ {{H}_{3}}C \end{smallmatrix}}{\mathop{C}}\,H\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{C}}\,C{{H}_{3}}}}\,\]
done
clear
View Answer play_arrow
question_answer 102) End product of the following reaction is:\[C{{H}_{3}}C{{H}_{2}}COOH\xrightarrow[red\,p]{C{{l}_{2}}}\] \[\xrightarrow[{}]{alcoholic\text{ }KOH}\]
A)
\[C{{H}_{3}}\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{C}}\,HCOOH\]
done
clear
B)
\[\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{C{{H}_{2}}}}\,C{{H}_{2}}COOH\]
done
clear
C)
\[C{{H}_{2}}=CHCOOH\]
done
clear
D)
\[\underset{\begin{smallmatrix} | \\ Cl \end{smallmatrix}}{\mathop{C{{H}_{2}}}}\,\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{CH}}\,COOH\]
done
clear
View Answer play_arrow
question_answer 103) For the following reaction in gaseous phase\[CO+\frac{1}{2}{{O}_{2}}\xrightarrow[{}]{{}}C{{O}_{2}}\]\[{{K}_{c}}/{{K}_{p}}\]is:
A)
\[{{(RT)}^{1/2}}\]
done
clear
B)
\[{{(RT)}^{-1/2}}\]
done
clear
C)
\[(RT)\]
done
clear
D)
\[{{(RT)}^{-1}}\]
done
clear
View Answer play_arrow
question_answer 104) Energy of H-atom in the ground state is\[-13.6\] eV, hence energy in the second excited state is:
A)
\[-6.8eV\]
done
clear
B)
\[-3.4eV\]
done
clear
C)
\[-1.51eV\]
done
clear
D)
\[-4.53eV\]
done
clear
View Answer play_arrow
question_answer 105) A square planar complex is formed by hybridisation of the following atomic orbitals:
A)
\[s,{{p}_{x}},{{p}_{y}},{{p}_{z}}\]
done
clear
B)
\[s,\text{ }{{p}_{x}}\text{ }{{p}_{y}},\text{ }{{p}_{z}}\text{, }d\]
done
clear
C)
\[d,\text{ s, }\,\text{ }{{p}_{x}},\text{ }{{p}_{y}}\]
done
clear
D)
\[\text{s, }{{p}_{x}},\text{ }{{p}_{y}},{{p}_{z}}\,d,\,d\]
done
clear
View Answer play_arrow
question_answer 106) Type of isomerism shown by\[[Cr{{(N{{H}_{3}})}_{5}}N{{O}_{2}}]C{{l}_{2}}\]is:
A)
optical
done
clear
B)
ionization
done
clear
C)
geometrical
done
clear
D)
linkage
done
clear
View Answer play_arrow
question_answer 107) One of the following equilibria is not affected by change in volume of the flask:
A)
\[PC{{l}_{5}}(g)PC{{l}_{3}}(g)+C{{l}_{2}}(g)\]
done
clear
B)
\[{{N}_{2}}(g)+3{{H}_{2}}(g)2N{{H}_{3}}(g)\]
done
clear
C)
\[{{N}_{2}}(g)+{{O}_{2}}(g)2NO(g)\]
done
clear
D)
\[S{{O}_{2}}C{{l}_{2}}(g)S{{O}_{2}}(g)+C{{l}_{2}}(g)\]
done
clear
View Answer play_arrow
question_answer 108) Uncertainty in position of a particle of 25 g in space is\[{{10}^{-5}}m\]. Hence uncertainty in velocity \[(m{{s}^{-1}})\]is (Plancks constant\[h=6.6\times {{10}^{-34}}Js\]):
A)
\[2.1\times {{10}^{-28}}\]
done
clear
B)
\[2.1\times {{10}^{-34}}\]
done
clear
C)
\[0.5\times {{10}^{-34}}\]
done
clear
D)
\[5.0\times {{10}^{-24}}\]
done
clear
View Answer play_arrow
question_answer 109) Consider the following reactions at\[1100{}^\circ C\] (I) \[2C+{{O}_{2}}\xrightarrow[{}]{{}}2CO,\]\[\Delta G{}^\circ =-460kJmo{{l}^{-1}}\] (II) \[2Zn+{{O}_{2}}\xrightarrow[{}]{{}}2ZnO,\]\[\Delta G{}^\circ =-360kJ\,mo{{l}^{-1}}\] Based on these, select correct alternate:
A)
zinc can be oxidised by\[CO\]
done
clear
B)
zinc oxide can be reduced by carbon
done
clear
C)
both are correct
done
clear
D)
none is correct
done
clear
View Answer play_arrow
question_answer 110) A reaction is non-spontaneous at the freezing point of water but is spontaneous at the boiling point of water then: \[\Delta H\] \[\Delta S\]
A)
\[+ve~~~~~~~~~~~+ve\]
done
clear
B)
\[-ve~~~~~~~~~~~-ve\]
done
clear
C)
\[-ve~~~~~~~~~~~+ve\]
done
clear
D)
\[+ve~~~~~~~~~~~-ve\]
done
clear
View Answer play_arrow
question_answer 111) If\[\alpha \ne \beta \]and\[{{\alpha }^{2}}=5\alpha -3,\text{ }{{\beta }^{2}}=5\beta -3,\]then the equation having\[\alpha /\beta \]and\[\beta /\alpha \]as its roots is:
A)
\[3{{x}^{2}}+19x+3=0\]
done
clear
B)
\[3{{x}^{2}}-19x+3=0\]
done
clear
C)
\[3{{x}^{2}}-19x-3=0\]
done
clear
D)
\[{{x}^{2}}-16x+1=0\]
done
clear
View Answer play_arrow
question_answer 112) If\[y={{(x+\sqrt{1+{{x}^{2}}})}^{n}},\]then \[(1+{{x}^{2}})\frac{{{d}^{2}}y}{d{{x}^{2}}}+x\frac{dy}{dx}\]is:
A)
\[{{n}^{2}}y\]
done
clear
B)
\[-{{n}^{2}}y\]
done
clear
C)
\[-y\]
done
clear
D)
\[2{{x}^{2}}y\]
done
clear
View Answer play_arrow
question_answer 113) If\[1,{{\log }_{3}}\sqrt{({{3}^{1-x}}+2)},{{\log }_{3}}({{4.3}^{x}}-1)\]are in A.P, then\[x\]equals:
A)
\[lo{{g}_{3}}4\]
done
clear
B)
\[1-lo{{g}_{3}}4\]
done
clear
C)
\[1-lo{{g}_{4}}3\]
done
clear
D)
\[lo{{g}_{4}}3\]
done
clear
View Answer play_arrow
question_answer 114) A problem in mathematics is given to three students A, B, C and their respective probability of solving the problem is\[\frac{1}{2},\frac{1}{3}\]and\[\frac{1}{4}\]. Probability that the problem is solved is:
A)
\[\frac{3}{4}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[\frac{2}{3}\]
done
clear
D)
\[\frac{1}{3}\]
done
clear
View Answer play_arrow
question_answer 115) The period of\[{{\sin }^{2}}\theta \]is:
A)
\[{{\pi }^{2}}\]
done
clear
B)
\[\pi \]
done
clear
C)
\[2\pi \]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 116) \[l,m,n\]are the\[{{p}^{th}},{{q}^{th}}\]and\[{{r}^{th}}\]term of an G.P. and all positive, then \[\left| \begin{matrix} \log l & p & 1 \\ \log m & q & 1 \\ \log n & r & 1 \\ \end{matrix} \right|\]equals:
A)
3
done
clear
B)
2
done
clear
C)
1
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 117) \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{1-\cos 2x}}{\sqrt{2}x}\]is:
A)
\[\lambda \]
done
clear
B)
\[-1\]
done
clear
C)
zero
done
clear
D)
does not exist
done
clear
View Answer play_arrow
question_answer 118) A triangle with vertices\[(4,0),(-1,-1),(3,5)\]is:
A)
isosceles and right angled
done
clear
B)
isosceles but not right angled
done
clear
C)
right angled but not isosceles
done
clear
D)
neither right angled nor isosceles
done
clear
View Answer play_arrow
question_answer 119) In a class of 100 students there are 70 boys whose average marks in a subject are 75. If the average marks of the complete class is 72, then what is the average of the girls?:
A)
73
done
clear
B)
65
done
clear
C)
68
done
clear
D)
74
done
clear
View Answer play_arrow
question_answer 120) \[{{\cot }^{-1}}(\sqrt{\cos \alpha })={{\tan }^{-1}}(\sqrt{\cos \alpha })=x,\]then\[\sin x\]is equal to:
A)
\[{{\tan }^{2}}\left( \frac{\alpha }{2} \right)\]
done
clear
B)
\[co{{t}^{2}}\left( \frac{\alpha }{2} \right)\]
done
clear
C)
\[\tan \alpha \]
done
clear
D)
\[\cot \left( \frac{\alpha }{2} \right)\]
done
clear
View Answer play_arrow
question_answer 121) The order and degree of the differential equation\[{{\left( 1+3\frac{dy}{dx} \right)}^{2/3}}=4\frac{{{d}^{2}}y}{d{{x}^{3}}}\]are:
A)
\[\left( 1,\frac{2}{3} \right)\]
done
clear
B)
\[(3,1)\]
done
clear
C)
\[(3,3)\]
done
clear
D)
\[(1,2)\]
done
clear
View Answer play_arrow
question_answer 122) A plane which passes through the point (3,2,0) and the line\[\frac{x-4}{1}=\frac{y-7}{5}=\frac{z-4}{4}\]is:
A)
\[x-y+z=1\]
done
clear
B)
\[x+y+z=5\]
done
clear
C)
\[x+2y-z=1\]
done
clear
D)
\[2x-y+z=5\]
done
clear
View Answer play_arrow
question_answer 123) The solution of the equation\[\frac{{{d}^{2}}y}{d{{x}^{2}}}={{e}^{-2x}}\]is:
A)
\[\frac{{{e}^{-2x}}}{4}\]
done
clear
B)
\[\frac{{{e}^{-2x}}}{4}+cx+d\]
done
clear
C)
\[\frac{1}{4}{{e}^{-2x}}+c{{x}^{2}}+d\]
done
clear
D)
\[\frac{1}{4}{{e}^{-2x}}+c+d\]
done
clear
View Answer play_arrow
question_answer 124) \[\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{{{x}^{2}}+5x+3}{{{x}^{2}}+x+2} \right)}^{x}}\]is equal to:
A)
\[{{e}^{4}}\]
done
clear
B)
\[{{e}^{2}}\]
done
clear
C)
\[{{e}^{3}}\]
done
clear
D)
\[e\]
done
clear
View Answer play_arrow
question_answer 125) The domain of\[{{\sin }^{-1}}[{{\log }_{3}}(x/3)]\]is:
A)
\[[1,9]\]
done
clear
B)
\[[-1,9]\]
done
clear
C)
\[[-9,1]\]
done
clear
D)
\[[-9,-1]\]
done
clear
View Answer play_arrow
question_answer 126) The value of\[{{2}^{1/4}}{{.4}^{1/8}}{{.8}^{1/6}}....\infty \]is:
A)
1
done
clear
B)
2
done
clear
C)
3/2
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 127) Fifth term of an G.P. is 2, then the product of its 9 terms is
A)
256
done
clear
B)
512
done
clear
C)
1024
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 128) \[\int_{0}^{10x}{|\sin x|dx}\]is:
A)
20
done
clear
B)
8
done
clear
C)
10
done
clear
D)
18
done
clear
View Answer play_arrow
question_answer 129) \[{{I}_{n}}=\int_{0}^{\pi /4}{{{\tan }^{n}}x}dx,\]then\[\underset{n\to \infty }{\mathop{\lim }}\,n[{{I}_{n}}+{{I}_{n+2}}]\]equals:
A)
\[\frac{1}{2}\]
done
clear
B)
1
done
clear
C)
\[\infty \]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 130) \[\int_{0}^{2}{[{{x}^{2}}]}\,dx\]is:
A)
\[2-\sqrt{2}\]
done
clear
B)
\[2+\sqrt{2}\]
done
clear
C)
\[\sqrt{2}-1\]
done
clear
D)
\[-\sqrt{2}-\sqrt{3}+5\]
done
clear
View Answer play_arrow
question_answer 131) .\[\int_{-\pi }^{\pi }{\frac{2x(1+\sin x)}{1+{{\cos }^{2}}x}}dx\]is:
A)
\[\frac{{{\pi }^{2}}}{4}\]
done
clear
B)
\[{{\pi }^{2}}\]
done
clear
C)
zero
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 132) The period of the function\[f(x)={{\sin }^{4}}x+{{\cos }^{4}}x\]is:
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[2\pi \]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 133) The domain of definition of the function\[f(x)=\sqrt{{{\log }_{10}}\left( \frac{5x-{{x}^{2}}}{4} \right)}\]is:
A)
[1, 4]
done
clear
B)
[1, 0]
done
clear
C)
[0, 5]
done
clear
D)
[5, 0]
done
clear
View Answer play_arrow
question_answer 134) If\[\sin y=a\sin (x+y),\]then\[\frac{dy}{dx}\]is:
A)
\[\frac{\sin a}{{{\sin }^{2}}(a+y)}\]
done
clear
B)
\[\frac{{{\sin }^{2}}(a+y)}{\sin a}\]
done
clear
C)
\[\sin a{{\sin }^{2}}(a+y)\]
done
clear
D)
\[\frac{{{\sin }^{2}}(a-y)}{\sin a}\]
done
clear
View Answer play_arrow
question_answer 135) If\[{{x}^{y}}={{e}^{x-y}}\]then\[\frac{dy}{dx}\]is:
A)
\[\frac{1+x}{1+\log x}\]
done
clear
B)
\[\frac{1-\log x}{1+\log x}\]
done
clear
C)
not defined
done
clear
D)
\[\frac{logx}{(1+\log x)}\]
done
clear
View Answer play_arrow
question_answer 136) The two curves\[{{x}^{3}}-3x{{y}^{2}}+2=0\]and\[3{{x}^{2}}y-{{y}^{3}}-2=0\]:
A)
cut at right angles
done
clear
B)
touch each other
done
clear
C)
cut at an angle\[\frac{\pi }{3}\]
done
clear
D)
cut at an angle\[\frac{\pi }{4}\]
done
clear
View Answer play_arrow
question_answer 137) The function\[f(x)={{\cot }^{-1}}x+x\]increases in the interval:
A)
\[(1,\infty )\]
done
clear
B)
\[(-1,\infty )\]
done
clear
C)
\[(-\infty ,\infty )\]
done
clear
D)
\[(0,\infty )\]
done
clear
View Answer play_arrow
question_answer 138) The greatest value of\[f(x)={{(x+1)}^{1/3}}-{{(x-1)}^{1/3}}\]on [0, 1] is:
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
1/3
done
clear
View Answer play_arrow
question_answer 139) Evaluate\[\int_{0}^{\pi /2}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}}dx\]:
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
zero
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 140) \[\int{\frac{dx}{x({{x}^{n}}+1)}}\]is equal to:
A)
\[\frac{1}{n}\log \left( \frac{{{x}^{n}}}{{{x}^{n}}+1} \right)+c\]
done
clear
B)
\[\frac{1}{n}\log \left( \frac{{{x}^{n}}+1}{{{x}^{n}}} \right)+c\]
done
clear
C)
\[\log \left( \frac{{{x}^{n}}}{{{x}^{n}}+1} \right)+c\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 141) The area bounded by the curve\[y=2x-x\] and the straight line\[y=-x\]is given by:
A)
\[\frac{9}{2}\]
done
clear
B)
\[\frac{43}{6}\]
done
clear
C)
\[\frac{35}{6}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 142) The differential equation of all non-vertical lines in a plane is:
A)
\[\frac{{{d}^{2}}y}{d{{x}^{2}}}=0\]
done
clear
B)
\[\frac{{{d}^{2}}x}{d{{y}^{2}}}=0\]
done
clear
C)
\[\frac{dy}{dx}=0\]
done
clear
D)
\[\frac{dx}{dy}=0\]
done
clear
View Answer play_arrow
question_answer 143) Given two vectors\[\hat{i}-\hat{j}\]and\[\hat{i}+2\hat{j}\]the unit vector coplanar with the two vectors and perpendicular to first is:
A)
\[\frac{1}{\sqrt{2}}(\hat{i}+\hat{j})\]
done
clear
B)
\[\frac{1}{\sqrt{5}}(2\hat{i}+\hat{j})\]
done
clear
C)
\[\pm \frac{1}{\sqrt{2}}(\hat{i}+\hat{k})\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 144) The vector\[\hat{i}+x\hat{j}+3\hat{k}\]is rotated through an angle\[\theta \]and doubled in magnitude, then it becomes\[4\hat{i}+(4x-2)\hat{i}+2\hat{k}\]. The value of\[x\] is:
A)
\[\left( -\frac{2}{3},2 \right)\]
done
clear
B)
\[\left( \frac{1}{3},2 \right)\]
done
clear
C)
\[\left( \frac{2}{3},0 \right)\]
done
clear
D)
\[(2,7)\]
done
clear
View Answer play_arrow
question_answer 145) A paralleiopiped is formed by planes drawn through the points (2,3,5) and (5,9,7), parallel to the coordinate planes. The length of a diagonal of the parallelepiped to piped is:
A)
\[7\]
done
clear
B)
\[\sqrt{38}\]
done
clear
C)
\[\sqrt{155}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 146) The equation of the plane containing the line \[\frac{x-{{x}_{1}}}{l}=\frac{y-{{y}_{1}}}{m}=\frac{z-{{z}_{1}}}{n}\]is\[a(x-{{x}_{1}})+b(y-{{y}_{1}})+c(z-{{z}_{1}})=0,\]where:
A)
\[a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}=0\]
done
clear
B)
\[al+bm+cn=0\]
done
clear
C)
\[\frac{a}{l}=\frac{b}{m}=\frac{c}{n}\]
done
clear
D)
\[l{{x}_{1}}+m{{y}_{1}}+n{{z}_{1}}=0\]
done
clear
View Answer play_arrow
question_answer 147) A and B play a game where each is asked to select a number from 1 to 25. If the two numbers match, both of them win a prize. The probability that they will not win a prize in a single trial is:
A)
\[\frac{1}{25}\]
done
clear
B)
\[\frac{24}{25}\]
done
clear
C)
\[\frac{2}{25}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 148) If A and B are two mutually exclusive events, then
A)
\[P(A)<P(\overline{B})\]
done
clear
B)
\[P(A)>P(\overline{B})\]
done
clear
C)
\[P(A)<P(B)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 149) The equation of the directrix of the parabola \[{{y}^{2}}+4v+4x+2=0\]is:
A)
\[x=-1\]
done
clear
B)
\[x=1\]
done
clear
C)
\[x=-\frac{3}{2}\]
done
clear
D)
\[x=\frac{3}{2}\]
done
clear
View Answer play_arrow
question_answer 150) Let\[{{T}_{n}}\]denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If\[{{T}_{n+1}}-{{T}_{n}}=21\]then\[n\] equals:
A)
5
done
clear
B)
7
done
clear
C)
6
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 151) In a triangle ABC, \[2ca\sin \frac{A-B+C}{2}\] is equal to:
A)
\[{{a}^{2}}+{{b}^{2}}-{{c}^{2}}\]
done
clear
B)
\[{{c}^{2}}+{{a}^{2}}-{{b}^{2}}\]
done
clear
C)
\[{{b}^{2}}-{{c}^{2}}-{{a}^{2}}\]
done
clear
D)
\[{{c}^{2}}-{{a}^{2}}-{{b}^{2}}.\]
done
clear
View Answer play_arrow
question_answer 152) For\[x\in R\,\,\underset{x\to \infty }{\mathop{\lim }}\,{{\left( \frac{x-3}{x+2} \right)}^{x}}\]is equal to:
A)
\[e\]
done
clear
B)
\[{{e}^{-1}}\]
done
clear
C)
\[{{e}^{-5}}\]
done
clear
D)
\[{{e}^{5}}\]
done
clear
View Answer play_arrow
question_answer 153) The in centre of the triangle with vertices \[(1,\sqrt{3}),(0,0)\]and\[(2,0)\]is:
A)
\[\left( 1,\frac{\sqrt{3}}{2} \right)\]
done
clear
B)
\[\left( \frac{2}{3},\frac{1}{\sqrt{3}} \right)\]
done
clear
C)
\[\left( \frac{2}{3},\frac{\sqrt{3}}{2} \right)\]
done
clear
D)
\[\left( 1,\frac{1}{\sqrt{3}} \right)\]
done
clear
View Answer play_arrow
question_answer 154) If the vectors\[\overrightarrow{a},\overrightarrow{b}\]and\[\overrightarrow{c}\]from the sides BC, CA and AB respectively, of a triangle ABC then:
A)
\[\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{c}.\overrightarrow{b}=0\]
done
clear
B)
\[\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{b}\times \overrightarrow{c}=\overrightarrow{c}\times \overrightarrow{a}\]
done
clear
C)
\[\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=0\]
done
clear
D)
\[\overrightarrow{a}\times \overrightarrow{a}+\overrightarrow{a}\times \overrightarrow{c}+\overrightarrow{c}\times \overrightarrow{a}=0\]
done
clear
View Answer play_arrow
question_answer 155) If\[\omega \]is an imaginary cube root of unity then \[{{(1+\omega +{{\omega }^{2}})}^{7}}\]equals:
A)
\[128\omega \]
done
clear
B)
\[-128\omega \]
done
clear
C)
\[128\,{{\omega }^{2}}\]
done
clear
D)
\[-128\,{{\omega }^{2}}\]
done
clear
View Answer play_arrow
question_answer 156) If\[\left| \begin{matrix} 6i & -3i & 1 \\ 4 & 3i & -1 \\ 20 & 3 & i \\ \end{matrix} \right|=x+iy\]then:
A)
\[x=3,y=1\]
done
clear
B)
\[x=1,y=3\]
done
clear
C)
\[x=0,\text{ y}=3\]
done
clear
D)
\[x=0,\text{ }y=0\]
done
clear
View Answer play_arrow
question_answer 157) \[{{\sin }^{2}}\theta =\frac{4xy}{{{(x+y)}^{2}}}\]is true if and only if:
A)
\[x+y\ne 0\]
done
clear
B)
\[x=y,x\ne 0,y\ne 0\]
done
clear
C)
\[x=y\]
done
clear
D)
\[x\ne 0,y\ne 0\]
done
clear
View Answer play_arrow
question_answer 158) The radius of the circle passing through the foci of the ellipse \[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{9}=1\]and having its centre at (0, 3) is:
A)
4
done
clear
B)
3
done
clear
C)
\[\sqrt{12}\]
done
clear
D)
\[\frac{7}{2}\]
done
clear
View Answer play_arrow
question_answer 159) The probability of India winning a test match against West-Indies is\[\frac{1}{2}\]assuming independence from match to match the probability that in a match series Indias second win occurs at the third test is:
A)
\[\frac{1}{8}\]
done
clear
B)
\[\frac{1}{4}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 160) If\[(\omega \ne 1)\]is a cubic root of unity, then\[\left| \begin{matrix} 1 & 1+i+{{\omega }^{2}} & {{\omega }^{2}} \\ 1-i & -1 & {{\omega }^{2}}-1 \\ -i & -1+\omega -i & -1 \\ \end{matrix} \right|\]equals:
A)
zero
done
clear
B)
1
done
clear
C)
\[i\]
done
clear
D)
\[\omega \]
done
clear
View Answer play_arrow
question_answer 161) A biased coin with probability\[p,0<p<1\]of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is\[\frac{2}{5},\]then p equals:
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{2}{3}\]
done
clear
C)
\[\frac{2}{5}\]
done
clear
D)
\[\frac{3}{5}\]
done
clear
View Answer play_arrow
question_answer 162) A fair die is tossed eight times. The probability that a third six is observed on the eight throw is:
A)
\[\frac{^{7}{{C}_{2}}\times {{5}^{5}}}{{{6}^{7}}}\]
done
clear
B)
\[\frac{^{7}{{C}_{2}}\times {{5}^{5}}}{{{6}^{8}}}\]
done
clear
C)
\[\frac{^{7}{{C}_{2}}\times {{5}^{5}}}{{{6}^{6}}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 163) Let\[f(2)=4\]and\[f(2)=4\]Then\[\underset{x\to 2}{\mathop{\lim }}\,\frac{xf(2)-2f(x)}{x-2}\]is given by:
A)
2
done
clear
B)
\[-2\]
done
clear
C)
\[-4\]
done
clear
D)
3
done
clear
View Answer play_arrow
question_answer 164) Three straight lines\[2x+11y-5=0,\] \[24x+7y-20=0\]and\[4x-3y-2=0\]:
A)
form a triangle
done
clear
B)
arc only concurrent
done
clear
C)
are concurrent with on line bisecting the angle between the other two
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 165) A straight line through the point (2, 2) intersects the lines\[\sqrt{3}x+y=0\]and \[\sqrt{3}x-y=0\]at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is:
A)
\[x-2=0\]
done
clear
B)
\[y-2=0\]
done
clear
C)
\[x+y-4=0\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 166) The greatest distance of the point\[P(10,7)\]from the circle\[{{x}^{2}}+{{y}^{2}}-4x-2y-20=0\]is:
A)
\[10\]
done
clear
B)
15
done
clear
C)
5
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 167) The equation of the tangent to the circle\[{{x}^{2}}+{{y}^{2}}+4x-4y+4=0\]which make equal intercepts on the positive coordinate axes is:
A)
\[x+y=2\]
done
clear
B)
\[x+y=2\sqrt{2}\]
done
clear
C)
\[x+y=4\]
done
clear
D)
\[x+y=8\]
done
clear
View Answer play_arrow
question_answer 168) The equation of the ellipse whose foci are \[(\pm ,2,0)\]and eccentricity\[\frac{1}{2}\]is:
A)
\[\frac{{{x}^{2}}}{12}+\frac{{{y}^{2}}}{16}=1\]
done
clear
B)
\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{12}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{8}=1\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 169) The equation of the chord joining two points \[({{x}_{1}},{{y}_{2}})\]and\[({{x}_{2}},{{y}_{2}})\]on the rectangular hyperbola\[xy={{c}^{2}}\]is:
A)
\[\frac{x}{{{x}_{1}}+{{x}_{2}}}+\frac{y}{{{y}_{1}}+{{y}_{2}}}=1\]
done
clear
B)
\[\frac{x}{{{x}_{1}}-{{x}_{2}}}+\frac{y}{{{y}_{1}}-{{y}_{2}}}=1\]
done
clear
C)
\[\frac{x}{{{y}_{1}}+{{y}_{2}}}+\frac{y}{{{x}_{1}}+{{x}_{2}}}=1\]
done
clear
D)
\[\frac{x}{{{y}_{1}}-{{y}_{2}}}+\frac{y}{{{x}_{1}}-{{x}_{2}}}=1\]
done
clear
View Answer play_arrow
question_answer 170) If the vectors\[\overrightarrow{c},\overrightarrow{a}=x\hat{i}+y\hat{j}+z\hat{j}\]and\[\hat{b}=\hat{j}\]are such that \[\overrightarrow{a},\overrightarrow{c}\] and\[\overrightarrow{b}\]form a right handed system then\[\overrightarrow{c}\]is:
A)
\[z\hat{j}-x\hat{k}\]
done
clear
B)
\[\overrightarrow{0}\]
done
clear
C)
\[y\hat{j}\]
done
clear
D)
\[-z\hat{i}+x\hat{k}\]
done
clear
View Answer play_arrow