 (2) The capacitance of a capacitor is defined as the magnitude of the charge Q on the positive plate divided by the magnitude of the potential difference V between the plates i.e., \[C=\frac{Q}{V}\]
(3) A capacitor get's charged when a battery is connected across the plates. Once capacitor get's fully charged, flow of charge carriers stops in the circuit and in this condition potential difference across the plates of capacitor is same as the potential difference across the terminals of battery.
(4) Net charge on a capacitor is always zero, but when we speak of the charge Q on a capacitor, we are referring to the magnitude of the charge on each plate.
(5) Energy stored : When a capacitor is charged by a voltage source (say battery) it stores the electric energy. If C = Capacitance of capacitor; Q = Charge on capacitor and V = Potential difference across capacitor then energy stored in capacitor \[U=\frac{1}{2}C{{V}^{2}}=\frac{1}{2}QV=\frac{{{Q}^{2}}}{2C}\]
In charging capacitor by battery half the energy supplied is stored in the capacitor and remaining half energy (1/2 QV) is lost in the form of heat.
(2) The capacitance of a capacitor is defined as the magnitude of the charge Q on the positive plate divided by the magnitude of the potential difference V between the plates i.e., \[C=\frac{Q}{V}\]
(3) A capacitor get's charged when a battery is connected across the plates. Once capacitor get's fully charged, flow of charge carriers stops in the circuit and in this condition potential difference across the plates of capacitor is same as the potential difference across the terminals of battery.
(4) Net charge on a capacitor is always zero, but when we speak of the charge Q on a capacitor, we are referring to the magnitude of the charge on each plate.
(5) Energy stored : When a capacitor is charged by a voltage source (say battery) it stores the electric energy. If C = Capacitance of capacitor; Q = Charge on capacitor and V = Potential difference across capacitor then energy stored in capacitor \[U=\frac{1}{2}C{{V}^{2}}=\frac{1}{2}QV=\frac{{{Q}^{2}}}{2C}\]
In charging capacitor by battery half the energy supplied is stored in the capacitor and remaining half energy (1/2 QV) is lost in the form of heat.  If these two spheres are connected through a conducting wire, then alteration of charge, potential and energy takes place.
If these two spheres are connected through a conducting wire, then alteration of charge, potential and energy takes place.
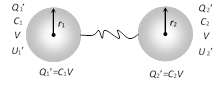 (1) New charge : According to the conservation of charge
\[{{Q}_{1}}+{{Q}_{2}}=Q_{1}^{'}+Q_{2}^{'}=Q\] (say), also \[\frac{Q_{1}^{'}}{Q_{2}^{'}}=\frac{{{C}_{1}}}{{{C}_{2}}}=\frac{{{r}_{1}}}{{{r}_{2}}}\]
\[\Rightarrow \]\[Q_{2}^{'}=Q\,\left[ \frac{{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \right]\] and similarly \[Q_{1}^{'}=Q\,\left[ \frac{{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}} \right]\]
(2) Common potential : Common potential
\[(V)=\frac{Total charge}{Total capacity}\]\[=\frac{{{Q}_{1}}+{{Q}_{2}}}{{{C}_{1}}+{{C}_{2}}}=\frac{Q_{1}^{'}+Q_{2}^{'}}{{{C}_{1}}+{{C}_{2}}}\]\[=\frac{{{C}_{1}}{{V}_{1}}+{{C}_{2}}{{V}_{2}}}{{{C}_{1}}+{{C}_{2}}}\]
(3) Energy loss : The loss of energy due to redistribution of charge is given by
\[\Delta \,U={{U}_{i}}-{{U}_{f}}=\frac{{{C}_{1}}{{C}_{2}}}{2({{C}_{1}}+{{C}_{2}})}\,{{({{V}_{1}}-{{V}_{2}})}^{2}}\]
(1) New charge : According to the conservation of charge
\[{{Q}_{1}}+{{Q}_{2}}=Q_{1}^{'}+Q_{2}^{'}=Q\] (say), also \[\frac{Q_{1}^{'}}{Q_{2}^{'}}=\frac{{{C}_{1}}}{{{C}_{2}}}=\frac{{{r}_{1}}}{{{r}_{2}}}\]
\[\Rightarrow \]\[Q_{2}^{'}=Q\,\left[ \frac{{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}} \right]\] and similarly \[Q_{1}^{'}=Q\,\left[ \frac{{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}} \right]\]
(2) Common potential : Common potential
\[(V)=\frac{Total charge}{Total capacity}\]\[=\frac{{{Q}_{1}}+{{Q}_{2}}}{{{C}_{1}}+{{C}_{2}}}=\frac{Q_{1}^{'}+Q_{2}^{'}}{{{C}_{1}}+{{C}_{2}}}\]\[=\frac{{{C}_{1}}{{V}_{1}}+{{C}_{2}}{{V}_{2}}}{{{C}_{1}}+{{C}_{2}}}\]
(3) Energy loss : The loss of energy due to redistribution of charge is given by
\[\Delta \,U={{U}_{i}}-{{U}_{f}}=\frac{{{C}_{1}}{{C}_{2}}}{2({{C}_{1}}+{{C}_{2}})}\,{{({{V}_{1}}-{{V}_{2}})}^{2}}\]  (1) Capacitance of a conductor : Charge given to a conductor increases it's potential i.e., \[Q\propto V\] \[\Rightarrow \] \[Q=CV\]
Where C is a proportionality constant, called capacity or capacitance of conductor. Hence capacitance is the ability of conductor to hold the charge.
(2) It's S.I. unit is \[\frac{Coulomb}{Volt}=Farad (F)\]
Smaller S.I. units are \[mF,\,\mu F,\,\,nF\] and pF (\[1mF={{10}^{-3}}F\], \[1\mu F={{10}^{-6}}F\], \[1nF={{10}^{-9}}F\], \[1pF=1\mu \mu F={{10}^{-12}}F\])
(3) It's C.G.S. unit is Stat Farad \[1F=9\times {{10}^{11}}\,Stat\,\,Farad\].
(4) It's dimension : \[[C]=[{{M}^{-1}}{{L}^{-2}}{{T}^{4}}{{A}^{2}}]\].
(5) Capacity of a body is independent of charge given to the body or it's potential raised and depends on shape and size only.
(6) Capacity of an isolated spherical conductor : When charge Q is given to a spherical conductor of radius R, then potential at the surface of sphere is \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{R}\] Þ \[\frac{Q}{V}=4\pi {{\varepsilon }_{0}}R\]
(1) Capacitance of a conductor : Charge given to a conductor increases it's potential i.e., \[Q\propto V\] \[\Rightarrow \] \[Q=CV\]
Where C is a proportionality constant, called capacity or capacitance of conductor. Hence capacitance is the ability of conductor to hold the charge.
(2) It's S.I. unit is \[\frac{Coulomb}{Volt}=Farad (F)\]
Smaller S.I. units are \[mF,\,\mu F,\,\,nF\] and pF (\[1mF={{10}^{-3}}F\], \[1\mu F={{10}^{-6}}F\], \[1nF={{10}^{-9}}F\], \[1pF=1\mu \mu F={{10}^{-12}}F\])
(3) It's C.G.S. unit is Stat Farad \[1F=9\times {{10}^{11}}\,Stat\,\,Farad\].
(4) It's dimension : \[[C]=[{{M}^{-1}}{{L}^{-2}}{{T}^{4}}{{A}^{2}}]\].
(5) Capacity of a body is independent of charge given to the body or it's potential raised and depends on shape and size only.
(6) Capacity of an isolated spherical conductor : When charge Q is given to a spherical conductor of radius R, then potential at the surface of sphere is \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{R}\] Þ \[\frac{Q}{V}=4\pi {{\varepsilon }_{0}}R\]
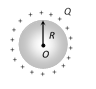 \[C=4\pi {{\varepsilon }_{0}}R=\frac{1}{9\times {{10}^{9}}}.R\]
If earth is assumed to be a conducting sphere having radius \[R=6400\,\,km.\] It's theoretical capacitance \[C=711\,\mu F\]. But for all practical purpose capacitance of earth is taken infinity and its potential \[V=0\]. (7) Energy of a charged conductor : Electrostatic potential energy of a conductor carrying charge Q, capacitance C and potential V is given by \[U=\frac{1}{2}QV=\frac{1}{2}C{{V}^{2}}=\frac{{{Q}^{2}}}{2C}\]
\[C=4\pi {{\varepsilon }_{0}}R=\frac{1}{9\times {{10}^{9}}}.R\]
If earth is assumed to be a conducting sphere having radius \[R=6400\,\,km.\] It's theoretical capacitance \[C=711\,\mu F\]. But for all practical purpose capacitance of earth is taken infinity and its potential \[V=0\]. (7) Energy of a charged conductor : Electrostatic potential energy of a conductor carrying charge Q, capacitance C and potential V is given by \[U=\frac{1}{2}QV=\frac{1}{2}C{{V}^{2}}=\frac{{{Q}^{2}}}{2C}\]  Flux from surface \[{{S}_{1}}=+\,\frac{Q}{{{\varepsilon }_{0}}},\] Flux from surface \[{{S}_{2}}=-\,\frac{Q}{{{\varepsilon }_{0}}},\] and flux from \[{{S}_{3}}=\] flux from surface \[{{S}_{4}}=0\]
Application of Gauss's law : See flux emergence in the following cases
(1) If a dipole is enclosed by a surface
Flux from surface \[{{S}_{1}}=+\,\frac{Q}{{{\varepsilon }_{0}}},\] Flux from surface \[{{S}_{2}}=-\,\frac{Q}{{{\varepsilon }_{0}}},\] and flux from \[{{S}_{3}}=\] flux from surface \[{{S}_{4}}=0\]
Application of Gauss's law : See flux emergence in the following cases
(1) If a dipole is enclosed by a surface
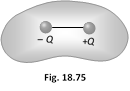 \[\because \,{{Q}_{enc}}=0\]
\[\Rightarrow \]\[\varphi =0\]
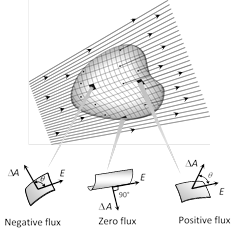
(2) The net charge \[{{Q}_{enc}}\] is the algebraic sum of all the enclosed positive, and negative charges. If \[{{Q}_{enc}}\] is positive the net flux is outward; if \[{{Q}_{enc}}\] is negative, the net flux is inward.
\[\because \,{{Q}_{enc}}=0\]
\[\Rightarrow \]\[\varphi =0\]
(2) The net charge \[{{Q}_{enc}}\] is the algebraic sum of all the enclosed positive, and negative charges. If \[{{Q}_{enc}}\] is positive the net flux is outward; if \[{{Q}_{enc}}\] is negative, the net flux is inward.
 \[\varphi =\frac{1}{{{\varepsilon }_{0}}}({{Q}_{1}}+{{Q}_{2}}-{{Q}_{3}})\]
(3) If a closed body (not enclosing any charge) is placed in an electric field (either uniform or non-uniform) total flux linked with it will be zero
(4) If a hemispherical body is placed in uniform electric field then flux linked with the curved surface calculated as follows
\[\varphi =\frac{1}{{{\varepsilon }_{0}}}({{Q}_{1}}+{{Q}_{2}}-{{Q}_{3}})\]
(3) If a closed body (not enclosing any charge) is placed in an electric field (either uniform or non-uniform) total flux linked with it will be zero
(4) If a hemispherical body is placed in uniform electric field then flux linked with the curved surface calculated as follows
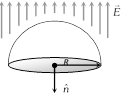 \[{{\varphi }_{Curved}}+{{\varphi }_{Circular}}=0\]
\[{{\varphi }_{Curved}}=-{{\varphi }_{Circular}}\]
\[=-\,(E\times \pi {{R}^{2}}\cos 180{}^\circ )\]
\[=+\pi {{R}^{2}}E\]
(5) If a hemispherical body is placed in non-uniform electric field as shown below. then flux linked with the circular surface calculated as follows
\[{{\varphi }_{Curved}}+{{\varphi }_{Circular}}=0\]
\[{{\varphi }_{Curved}}=-{{\varphi }_{Circular}}\]
\[=-\,(E\times \pi {{R}^{2}}\cos 180{}^\circ )\]
\[=+\pi {{R}^{2}}E\]
(5) If a hemispherical body is placed in non-uniform electric field as shown below. then flux linked with the circular surface calculated as follows
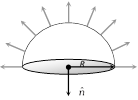 \[{{\varphi }_{Circular}}=-{{\varphi }_{Curved}}\]
\[{{\varphi }_{Circular}}=-\,(E\times 2\pi {{R}^{2}}\cos 0{}^\circ )\]
\[=-\,2\pi {{R}^{2}}E\]
(6) If charge is kept at the centre of cube
\[{{\varphi }_{Circular}}=-{{\varphi }_{Curved}}\]
\[{{\varphi }_{Circular}}=-\,(E\times 2\pi {{R}^{2}}\cos 0{}^\circ )\]
\[=-\,2\pi {{R}^{2}}E\]
(6) If charge is kept at the centre of cube
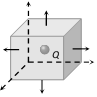 \[{{\varphi }_{total}}=\frac{1}{{{\varepsilon }_{0}}}.(Q)\]
\[{{\varphi }_{face}}=\frac{Q}{6{{\varepsilon }_{0}}}\]
\[{{\varphi }_{corner}}=\frac{Q}{8{{\varepsilon }_{0}}}\]
\[{{\varphi }_{edge}}=\frac{Q}{12{{\varepsilon }_{0}}}\]
(7) If charge is kept at the centre of a face : First we should enclosed the charge by assuming a Gaussian surface (an identical imaginary cube)
\[{{\varphi }_{total}}=\frac{1}{{{\varepsilon }_{0}}}.(Q)\]
\[{{\varphi }_{face}}=\frac{Q}{6{{\varepsilon }_{0}}}\]
\[{{\varphi }_{corner}}=\frac{Q}{8{{\varepsilon }_{0}}}\]
\[{{\varphi }_{edge}}=\frac{Q}{12{{\varepsilon }_{0}}}\]
(7) If charge is kept at the centre of a face : First we should enclosed the charge by assuming a Gaussian surface (an identical imaginary cube)
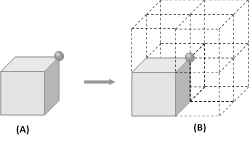
 Total flux emerges from the system (Two cubes) \[{{\varphi }_{total}}=\frac{Q}{{{\varepsilon }_{0}}}\]
Flux from given cube (i.e. from 5 face only) \[{{\varphi }_{cube}}=\frac{Q}{2{{\varepsilon }_{0}}}\]
(8) If a charge is kept at the corner of a cube
Total flux emerges from the system (Two cubes) \[{{\varphi }_{total}}=\frac{Q}{{{\varepsilon }_{0}}}\]
Flux from given cube (i.e. from 5 face only) \[{{\varphi }_{cube}}=\frac{Q}{2{{\varepsilon }_{0}}}\]
(8) If a charge is kept at the corner of a cube
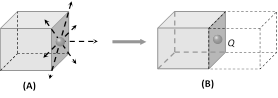
 For enclosing the charge seven more cubes are required so total flux from the 8 cube system is \[{{\phi }_{1}}=\frac{Q}{{{\varepsilon }_{0}}}\]. Flux from given cube \[{{\varphi }_{cube}}=\frac{Q}{8{{\varepsilon }_{0}}}\]. Flux from one more...
For enclosing the charge seven more cubes are required so total flux from the 8 cube system is \[{{\phi }_{1}}=\frac{Q}{{{\varepsilon }_{0}}}\]. Flux from given cube \[{{\varphi }_{cube}}=\frac{Q}{8{{\varepsilon }_{0}}}\]. Flux from one more... 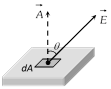 \[\varphi =E.A\cos \theta \] or \[\varphi =\overrightarrow{E}.\overrightarrow{A}\]
(2) In case of variable electric field or curved area. \[\varphi =\int{\overrightarrow{E}.\,\overrightarrow{dA}}\]
(3) It's S.I. Unit is (Volt \[\times \] m) or \[\frac{N\text{-}{{m}^{2}}}{C}\]
(4) For a closed body outward flux is taken to be positive while inward flux is taken to be negative.
\[\varphi =E.A\cos \theta \] or \[\varphi =\overrightarrow{E}.\overrightarrow{A}\]
(2) In case of variable electric field or curved area. \[\varphi =\int{\overrightarrow{E}.\,\overrightarrow{dA}}\]
(3) It's S.I. Unit is (Volt \[\times \] m) or \[\frac{N\text{-}{{m}^{2}}}{C}\]
(4) For a closed body outward flux is taken to be positive while inward flux is taken to be negative.
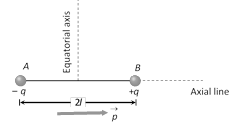 (1) Dipole moment : It is a vector quantity and is directed from negative charge to positive charge along the axis. It is denoted as \[\vec{p}\] and is defined as the product of the magnitude of either of the charge and the dipole length i.e. \[\vec{p}=q\,(2\vec{l})\]
Its S.I. unit is coulomb-metre or Debye (1 Debye \[=3.3\times {{10}^{-30}}\,C\times m\] ) and its dimensions are \[{{M}^{0}}{{L}^{1}}{{T}^{1}}{{A}^{1}}\].
(2) When a dielectric is placed in an electric field, its atoms or molecules are considered as tiny dipoles.
(1) Dipole moment : It is a vector quantity and is directed from negative charge to positive charge along the axis. It is denoted as \[\vec{p}\] and is defined as the product of the magnitude of either of the charge and the dipole length i.e. \[\vec{p}=q\,(2\vec{l})\]
Its S.I. unit is coulomb-metre or Debye (1 Debye \[=3.3\times {{10}^{-30}}\,C\times m\] ) and its dimensions are \[{{M}^{0}}{{L}^{1}}{{T}^{1}}{{A}^{1}}\].
(2) When a dielectric is placed in an electric field, its atoms or molecules are considered as tiny dipoles.
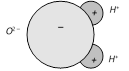
 Water \[({{H}_{2}}O),\] Chloroform \[(CHC{{l}_{3}}),\] Ammonia \[(N{{H}_{3}}),\,HCl,\,CO\] molecules are some example of permanent electric dipole.
Water \[({{H}_{2}}O),\] Chloroform \[(CHC{{l}_{3}}),\] Ammonia \[(N{{H}_{3}}),\,HCl,\,CO\] molecules are some example of permanent electric dipole.
 (3) Electric field and potential due to an electric dipole : If a, e and g are three points on axial, equatorial and general position at a distance r from the centre of dipole
(3) Electric field and potential due to an electric dipole : If a, e and g are three points on axial, equatorial and general position at a distance r from the centre of dipole
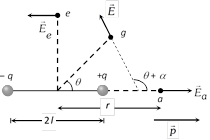 (i) At axial point : Electric field and potential are given as
\[{{E}_{a}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{2p}{{{r}^{3}}}\] (directed from \[-q\] to +q)
\[{{V}_{a}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{2}}}\]. Angle between \[{{\overrightarrow{E}}_{a}}\] and \[\overrightarrow{p\,}\] is \[{{0}^{o}}\].
(ii) At equatorial point : \[{{E}_{e}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{3}}}\] (directed from +q to \[-q\]) and \[{{V}_{e}}=0\]. Angle between \[{{\overrightarrow{E}}_{e}}\] and \[\vec{p}\] is \[{{180}^{o}}\].
(iii) At general point : \[{{E}_{g}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{3}}}\sqrt{(3{{\cos }^{2}}\theta +1)}\] and \[{{V}_{g}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p\cos \theta }{{{r}^{2}}}\]. Angle between \[\overrightarrow{E}\] and \[\overrightarrow{p}\] is \[(\theta +\alpha )\](where \[\tan \alpha =\frac{1}{2}\tan \theta \])
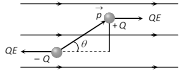
(4) Dipole in an external electric field : When a dipole is kept in an uniform electric field. The net force experienced by the dipole is zero as shown in fig.
The net torque experienced by the dipole is
\[\tau =pE\sin \theta \]
\[\overrightarrow{\tau }=\overrightarrow{p}\times \overrightarrow{E}\]
(i) At axial point : Electric field and potential are given as
\[{{E}_{a}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{2p}{{{r}^{3}}}\] (directed from \[-q\] to +q)
\[{{V}_{a}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{2}}}\]. Angle between \[{{\overrightarrow{E}}_{a}}\] and \[\overrightarrow{p\,}\] is \[{{0}^{o}}\].
(ii) At equatorial point : \[{{E}_{e}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{3}}}\] (directed from +q to \[-q\]) and \[{{V}_{e}}=0\]. Angle between \[{{\overrightarrow{E}}_{e}}\] and \[\vec{p}\] is \[{{180}^{o}}\].
(iii) At general point : \[{{E}_{g}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p}{{{r}^{3}}}\sqrt{(3{{\cos }^{2}}\theta +1)}\] and \[{{V}_{g}}=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{p\cos \theta }{{{r}^{2}}}\]. Angle between \[\overrightarrow{E}\] and \[\overrightarrow{p}\] is \[(\theta +\alpha )\](where \[\tan \alpha =\frac{1}{2}\tan \theta \])
(4) Dipole in an external electric field : When a dipole is kept in an uniform electric field. The net force experienced by the dipole is zero as shown in fig.
The net torque experienced by the dipole is
\[\tau =pE\sin \theta \]
\[\overrightarrow{\tau }=\overrightarrow{p}\times \overrightarrow{E}\]
 Hence due to torque so produced, dipole align itself in the direction of electric field. This is the position of stable equilibrium of dipole.
(i) Work done in rotation : Suppose initially, dipole is kept in a uniform electric field at an angle \[{{\theta }_{1}}\]. Now to turn it through an angle \[{{\theta }_{2}}\] (with the field) Work done \[W=pE(\cos {{\theta }_{1}}-\cos {{\theta }_{2}})\].
Hence due to torque so produced, dipole align itself in the direction of electric field. This is the position of stable equilibrium of dipole.
(i) Work done in rotation : Suppose initially, dipole is kept in a uniform electric field at an angle \[{{\theta }_{1}}\]. Now to turn it through an angle \[{{\theta }_{2}}\] (with the field) Work done \[W=pE(\cos {{\theta }_{1}}-\cos {{\theta }_{2}})\].
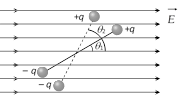 If \[{{\theta }_{1}}={{0}^{o}}\] and \[{{\theta }_{2}}=\theta \] i.e. initially dipole is kept along the field then it turn through \[\theta \] so work done \[W=pE(1-\cos \theta )\]
(ii) Potential energy of dipole : It is defined as work done in rotating a dipole from a direction perpendicular to the field to the given direction, i.e. from above formula of work.
If \[{{\theta }_{1}}={{90}^{o}}\] and \[{{\theta }_{2}}=\theta \Rightarrow W=U-pE\cos \theta \]
If \[{{\theta }_{1}}={{0}^{o}}\] and \[{{\theta }_{2}}=\theta \] i.e. initially dipole is kept along the field then it turn through \[\theta \] so work done \[W=pE(1-\cos \theta )\]
(ii) Potential energy of dipole : It is defined as work done in rotating a dipole from a direction perpendicular to the field to the given direction, i.e. from above formula of work.
If \[{{\theta }_{1}}={{90}^{o}}\] and \[{{\theta }_{2}}=\theta \Rightarrow W=U-pE\cos \theta \]
| more...
(1) For a charged soap bubble of radius R and surface tension T and charge density \[\sigma .\] The pressure due to surface tension \[4\frac{T}{R}\] and atmospheric pressure \[{{P}_{\text{out}}}\] act radially inwards and the electrical pressure \[({{P}_{el}})\] acts radially outward.
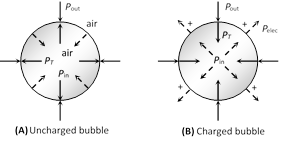 (2) The total pressure inside the soap bubble
\[{{P}_{\text{in}}}={{P}_{\text{out}}}+\frac{4T}{R}-\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(3) Excess pressure inside the charged soap bubble
\[{{P}_{\text{in}}}-{{P}_{\text{out}}}\,\,={{P}_{\text{excess}}}=\frac{4T}{R}-\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\].
(4) If air pressure inside and outside are assumed equal then \[{{P}_{\text{in}}}={{P}_{\text{out}}}\]i.e.,\[{{P}_{\text{excess}}}=0\]. So, \[\frac{4T}{R}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(i) Charge density : Since \[\frac{4T}{R}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]\[\Rightarrow \]\[\sigma \,=\sqrt{\frac{8{{\varepsilon }_{0}}T}{R}}=\sqrt{\frac{2T}{\pi kR}}\]
(ii) Radius of bubble \[R=\frac{8\,{{\varepsilon }_{0}}\,T}{{{\sigma }^{2}}}\]
(iii) Surface tension \[T=\frac{{{\sigma }^{2}}R}{8{{\varepsilon }_{0}}}\]
(iv) Total charge on the bubble \[Q=8\pi R\sqrt{2{{\varepsilon }_{0}}TR}\]
(v) Electric field intensity at the surface of the bubble
\[E=\sqrt{\frac{8T}{{{\varepsilon }_{0}}R}}=\sqrt{\frac{32\pi \,kT}{R}}\]
(vi) Electric potential at the surface \[V=\sqrt{32\pi RTk}=\sqrt{\frac{8RT}{{{\varepsilon }_{0}}}}\]
(2) The total pressure inside the soap bubble
\[{{P}_{\text{in}}}={{P}_{\text{out}}}+\frac{4T}{R}-\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(3) Excess pressure inside the charged soap bubble
\[{{P}_{\text{in}}}-{{P}_{\text{out}}}\,\,={{P}_{\text{excess}}}=\frac{4T}{R}-\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\].
(4) If air pressure inside and outside are assumed equal then \[{{P}_{\text{in}}}={{P}_{\text{out}}}\]i.e.,\[{{P}_{\text{excess}}}=0\]. So, \[\frac{4T}{R}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(i) Charge density : Since \[\frac{4T}{R}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]\[\Rightarrow \]\[\sigma \,=\sqrt{\frac{8{{\varepsilon }_{0}}T}{R}}=\sqrt{\frac{2T}{\pi kR}}\]
(ii) Radius of bubble \[R=\frac{8\,{{\varepsilon }_{0}}\,T}{{{\sigma }^{2}}}\]
(iii) Surface tension \[T=\frac{{{\sigma }^{2}}R}{8{{\varepsilon }_{0}}}\]
(iv) Total charge on the bubble \[Q=8\pi R\sqrt{2{{\varepsilon }_{0}}TR}\]
(v) Electric field intensity at the surface of the bubble
\[E=\sqrt{\frac{8T}{{{\varepsilon }_{0}}R}}=\sqrt{\frac{32\pi \,kT}{R}}\]
(vi) Electric potential at the surface \[V=\sqrt{32\pi RTk}=\sqrt{\frac{8RT}{{{\varepsilon }_{0}}}}\]
To find force on a charged conductor (due to repulsion of like charges) imagine a small part XY to be cut and just separated from the rest of the conductor MLN. The field in the cavity due to the rest of the conductor is \[{{E}_{2}},\] while field due to small part is \[{{E}_{1}}\]. Then
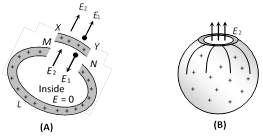 Inside the conductor \[E={{E}_{1}}-{{E}_{2}}=0\] or \[{{E}_{1}}={{E}_{2}}\]
Outside the conductor \[E={{E}_{1}}+{{E}_{2}}=\frac{\sigma }{{{\varepsilon }_{0}}}\]
Thus \[{{E}_{1}}={{E}_{2}}=\frac{\sigma }{2{{\varepsilon }_{0}}}\]
(1) To find force, imagine charged part XY (having charge \[\sigma \,dA\] placed in the cavity MN having field \[{{E}_{2}}\]). Thus force \[dF=(\sigma \,dA){{E}_{2}}\] or \[dF=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}dA\]. The force per unit area or electrostatic pressure \[p=\frac{dF}{dA}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(2) The force is always outwards as \[{{(\pm \sigma )}^{2}}\] is positive i.e., whether charged positively or negatively, this force will try to expand the charged body. [A soap bubble or rubber balloon expands on charging to it (charge of any kind + or \[-\])].
Inside the conductor \[E={{E}_{1}}-{{E}_{2}}=0\] or \[{{E}_{1}}={{E}_{2}}\]
Outside the conductor \[E={{E}_{1}}+{{E}_{2}}=\frac{\sigma }{{{\varepsilon }_{0}}}\]
Thus \[{{E}_{1}}={{E}_{2}}=\frac{\sigma }{2{{\varepsilon }_{0}}}\]
(1) To find force, imagine charged part XY (having charge \[\sigma \,dA\] placed in the cavity MN having field \[{{E}_{2}}\]). Thus force \[dF=(\sigma \,dA){{E}_{2}}\] or \[dF=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}dA\]. The force per unit area or electrostatic pressure \[p=\frac{dF}{dA}=\frac{{{\sigma }^{2}}}{2{{\varepsilon }_{0}}}\]
(2) The force is always outwards as \[{{(\pm \sigma )}^{2}}\] is positive i.e., whether charged positively or negatively, this force will try to expand the charged body. [A soap bubble or rubber balloon expands on charging to it (charge of any kind + or \[-\])].
(1) Work done in bringing the given charge from infinity to a point in the electric field is known as potential energy of the charge. Potential can also be written as potential energy per unit charge. i.e. \[V=\frac{W}{Q}=\frac{U}{Q}\].
(2) Potential energy of a system of two charge
Potential energy of \[{{Q}_{1}}=\] Potential energy of \[{{Q}_{2}}=\] potential energy of system \[U=k\frac{{{Q}_{1}}{{Q}_{2}}}{r}\]
In C.G.S. \[U=\frac{{{Q}_{1}}{{Q}_{2}}}{r}\]
Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |