
 where \[S\equiv \frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}-1\]
\[{{S}_{1}}\equiv \frac{x_{1}^{2}}{{{a}^{2}}}+\frac{y_{1}^{2}}{{{b}^{2}}}-1\]
\[T\equiv \frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}-1\]
Director circle: The director circle is the locus of points from which perpendicular tangents are drawn to the ellipse.
Hence locus of \[P({{x}_{1}},{{y}_{1}})\]i.e., equation of director circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}+{{b}^{2}}\].
where \[S\equiv \frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}-1\]
\[{{S}_{1}}\equiv \frac{x_{1}^{2}}{{{a}^{2}}}+\frac{y_{1}^{2}}{{{b}^{2}}}-1\]
\[T\equiv \frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}-1\]
Director circle: The director circle is the locus of points from which perpendicular tangents are drawn to the ellipse.
Hence locus of \[P({{x}_{1}},{{y}_{1}})\]i.e., equation of director circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}+{{b}^{2}}\]. 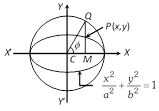 If \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is an ellipse, then its auxiliary circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\].
Eccentric angle of a point: Let P be any point on the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]. Draw PM perpendicular from P on the major axis of the ellipse and produce MP to meet the auxiliary circle in Q. Join CQ. The angle \[\angle XCQ=\varphi \] is called the eccentric angle of the point P on the ellipse.
Note that the angle \[\angle XCP\] is not the eccentric angle of point P.
If \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is an ellipse, then its auxiliary circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\].
Eccentric angle of a point: Let P be any point on the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]. Draw PM perpendicular from P on the major axis of the ellipse and produce MP to meet the auxiliary circle in Q. Join CQ. The angle \[\angle XCQ=\varphi \] is called the eccentric angle of the point P on the ellipse.
Note that the angle \[\angle XCP\] is not the eccentric angle of point P. 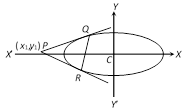
 where \[T=\frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}-1\], \[{{S}_{1}}=\frac{x_{1}^{2}}{{{a}^{2}}}+\frac{y_{1}^{2}}{{{b}^{2}}}-1\].
where \[T=\frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}-1\], \[{{S}_{1}}=\frac{x_{1}^{2}}{{{a}^{2}}}+\frac{y_{1}^{2}}{{{b}^{2}}}-1\]. 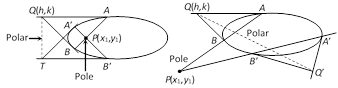 Equation of polar : Equation of polar of the point \[({{x}_{1}},{{y}_{1}})\] with respect to ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is given by
\[\frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}=1\], i.e., \[T=0\].
Coordinates of pole: The pole of the line \[lx+my+n=0\] with respect to ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[P\left( \frac{-{{a}^{2}}l}{n},\frac{-{{b}^{2}}m}{n} \right)\].
Properties of pole and polar
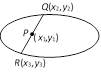
(1) If the polar of \[P({{x}_{1}},{{y}_{1}})\]passes through \[Q({{x}_{2}},{{y}_{2}})\], then the polar of \[Q({{x}_{2}},{{y}_{2}})\]goes through \[P({{x}_{1}},{{y}_{1}})\] and such points are said to be conjugate points.
(2) If the pole of a line \[{{l}_{1}}x+{{m}_{1}}y+{{n}_{1}}=0\]lies on the another line \[{{l}_{2}}x+{{m}_{2}}y+{{n}_{2}}=0\], then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
(3) Pole of a given line is same as point of intersection of tangents at its extremities.
Equation of polar : Equation of polar of the point \[({{x}_{1}},{{y}_{1}})\] with respect to ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is given by
\[\frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}=1\], i.e., \[T=0\].
Coordinates of pole: The pole of the line \[lx+my+n=0\] with respect to ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[P\left( \frac{-{{a}^{2}}l}{n},\frac{-{{b}^{2}}m}{n} \right)\].
Properties of pole and polar
(1) If the polar of \[P({{x}_{1}},{{y}_{1}})\]passes through \[Q({{x}_{2}},{{y}_{2}})\], then the polar of \[Q({{x}_{2}},{{y}_{2}})\]goes through \[P({{x}_{1}},{{y}_{1}})\] and such points are said to be conjugate points.
(2) If the pole of a line \[{{l}_{1}}x+{{m}_{1}}y+{{n}_{1}}=0\]lies on the another line \[{{l}_{2}}x+{{m}_{2}}y+{{n}_{2}}=0\], then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
(3) Pole of a given line is same as point of intersection of tangents at its extremities. You need to login to perform this action.
You will be redirected in
3 sec
