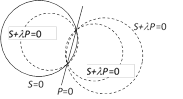
 (1) The equation of a system of co-axial circles, when the equation of the radical axis and of one circle of the system are \[P\equiv lx+my+n=0\], \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] respectively, is \[S+\lambda P=0\,\,\] \[(\lambda \] is an arbitrary constant).
(2) The equation of a co-axial system of circles, where the equation of any two circles of the system are
\[{{S}_{1}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\]
and \[{{S}_{2}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\]
Respectively, is \[{{S}_{1}}+\lambda \,({{S}_{1}}-{{S}_{2}})=0\]
or \[{{S}_{2}}+{{\lambda }_{1}}\,({{S}_{1}}-{{S}_{2}})=0\]
(1) The equation of a system of co-axial circles, when the equation of the radical axis and of one circle of the system are \[P\equiv lx+my+n=0\], \[S\equiv {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] respectively, is \[S+\lambda P=0\,\,\] \[(\lambda \] is an arbitrary constant).
(2) The equation of a co-axial system of circles, where the equation of any two circles of the system are
\[{{S}_{1}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\]
and \[{{S}_{2}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\]
Respectively, is \[{{S}_{1}}+\lambda \,({{S}_{1}}-{{S}_{2}})=0\]
or \[{{S}_{2}}+{{\lambda }_{1}}\,({{S}_{1}}-{{S}_{2}})=0\]
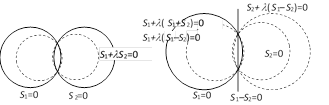 Other form \[{{S}_{1}}+\lambda {{S}_{2}}=0,\,\,\,\,\,(\lambda \ne -1)\]
(3) The equation of a system of co-axial circles in the simplest form is \[{{x}^{2}}+{{y}^{2}}+2gx+c=0\], where g is a variable and c is a constant.
Other form \[{{S}_{1}}+\lambda {{S}_{2}}=0,\,\,\,\,\,(\lambda \ne -1)\]
(3) The equation of a system of co-axial circles in the simplest form is \[{{x}^{2}}+{{y}^{2}}+2gx+c=0\], where g is a variable and c is a constant.
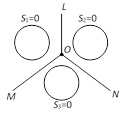 Let the straight lines i.e., OL and OM meet in O. The equation of any straight line passing through O is \[{{x}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}}{2}\], where \[\lambda \] is any constant.
For \[\lambda =1\], this equation become \[{{S}_{2}}-{{S}_{3}}=0\], which is, equation of ON.
Thus the third radical axis also passes through the point where the straight lines OL and OM meet.
In the above figure O is the radical centre.
Properties of radical centre
(i) Co-ordinates of radical centre can be found by solving the equations \[{{S}_{1}}={{S}_{2}}={{S}_{3}}\].
(ii) The radical centre of three circles described on the sides of a triangle as diameters is the orthocentre of the triangle.
Let the straight lines i.e., OL and OM meet in O. The equation of any straight line passing through O is \[{{x}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}}{2}\], where \[\lambda \] is any constant.
For \[\lambda =1\], this equation become \[{{S}_{2}}-{{S}_{3}}=0\], which is, equation of ON.
Thus the third radical axis also passes through the point where the straight lines OL and OM meet.
In the above figure O is the radical centre.
Properties of radical centre
(i) Co-ordinates of radical centre can be found by solving the equations \[{{S}_{1}}={{S}_{2}}={{S}_{3}}\].
(ii) The radical centre of three circles described on the sides of a triangle as diameters is the orthocentre of the triangle. 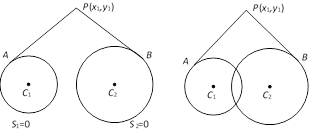 The equation of the radical axis of the two circle is \[{{S}_{1}}-{{S}_{2}}=0\] i.e., \[2x({{g}_{1}}-{{g}_{2}})+2y({{f}_{1}}-{{f}_{2}})+{{c}_{1}}-{{c}_{2}}=0\], which is a straight line.
Properties of the radical axis
(i) The radical axis and common chord are identical for two intersecting circles.
(ii) The radical axis is perpendicular to the straight line which joins the centres of the circles.
(iii) If two circles cut a third circle orthogonally, the radical axis of the two circles will pass through the centre of the third circle.
The equation of the radical axis of the two circle is \[{{S}_{1}}-{{S}_{2}}=0\] i.e., \[2x({{g}_{1}}-{{g}_{2}})+2y({{f}_{1}}-{{f}_{2}})+{{c}_{1}}-{{c}_{2}}=0\], which is a straight line.
Properties of the radical axis
(i) The radical axis and common chord are identical for two intersecting circles.
(ii) The radical axis is perpendicular to the straight line which joins the centres of the circles.
(iii) If two circles cut a third circle orthogonally, the radical axis of the two circles will pass through the centre of the third circle.  (2) The equation of the family of circles passing through the point of intersection of circle S = 0 and a line L = 0 is given as \[S+\lambda L=0\], (where \[\lambda \] is a parameter)
(2) The equation of the family of circles passing through the point of intersection of circle S = 0 and a line L = 0 is given as \[S+\lambda L=0\], (where \[\lambda \] is a parameter)
 (3) The equation of the family of circles touching the circle \[S=0\] and the line \[L=0\] at their point of contact P is \[S+\lambda L=0\], (where \[\lambda \] is a parameter)
(3) The equation of the family of circles touching the circle \[S=0\] and the line \[L=0\] at their point of contact P is \[S+\lambda L=0\], (where \[\lambda \] is a parameter)
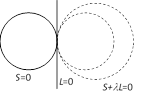 (4) The equation of a family of circles passing through two given points \[P\,({{x}_{1}},\,{{y}_{1}})\] and \[Q\,({{x}_{2}},\,{{y}_{2}})\] can be written in the form \[(x-{{x}_{1}})\,(x-{{x}_{2}})+(y-{{y}_{1}})\,(y-{{y}_{2}})+\lambda \,\left| \,\begin{matrix} x & y & 1 \\ {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ \end{matrix}\, \right|\,=0\] , (where \[\lambda \] is a parameter)
(4) The equation of a family of circles passing through two given points \[P\,({{x}_{1}},\,{{y}_{1}})\] and \[Q\,({{x}_{2}},\,{{y}_{2}})\] can be written in the form \[(x-{{x}_{1}})\,(x-{{x}_{2}})+(y-{{y}_{1}})\,(y-{{y}_{2}})+\lambda \,\left| \,\begin{matrix} x & y & 1 \\ {{x}_{1}} & {{y}_{1}} & 1 \\ {{x}_{2}} & {{y}_{2}} & 1 \\ \end{matrix}\, \right|\,=0\] , (where \[\lambda \] is a parameter)
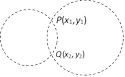 (5) The equation of family of circles, which touch \[y-{{y}_{1}}=m\,(x-{{x}_{1}})\] at \[({{x}_{1}},\,{{y}_{1}})\] for any finite m is \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}+\lambda \,\{(y-{{y}_{1}})\]\[-m\,(x-{{x}_{1}})\}=0\]
And if \[m\] is infinite, the family of circles is
\[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}+\lambda \,(x-{{x}_{1}})=0\], (where \[\lambda \] is a parameter)
(5) The equation of family of circles, which touch \[y-{{y}_{1}}=m\,(x-{{x}_{1}})\] at \[({{x}_{1}},\,{{y}_{1}})\] for any finite m is \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}+\lambda \,\{(y-{{y}_{1}})\]\[-m\,(x-{{x}_{1}})\}=0\]
And if \[m\] is infinite, the family of circles is
\[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}+\lambda \,(x-{{x}_{1}})=0\], (where \[\lambda \] is a parameter)
 (6) Equation of the circles given in diagram is
\[(x-{{x}_{1}})\,(x-{{x}_{2}})+\]\[(y-{{y}_{1}})\,(y-{{y}_{2}})\,\pm \cot \theta \,\{(x-{{x}_{1}})\,(y-{{y}_{2}})\]\[-(x-{{x}_{2}})\,(y-{{y}_{1}})\}=0\]
(6) Equation of the circles given in diagram is
\[(x-{{x}_{1}})\,(x-{{x}_{2}})+\]\[(y-{{y}_{1}})\,(y-{{y}_{2}})\,\pm \cot \theta \,\{(x-{{x}_{1}})\,(y-{{y}_{2}})\]\[-(x-{{x}_{2}})\,(y-{{y}_{1}})\}=0\]
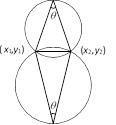
 If \[S\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\]
\[S'\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\]
are two circles with radii \[{{r}_{1}},\,\,{{r}_{2}}\] and d be the distance between their centres then the angle of intersection \[\theta \] between them is given by \[\cos \theta =\frac{r_{1}^{2}+r_{2}^{2}-{{d}^{2}}}{2{{r}_{1}}{{r}_{2}}}\] or \[\cos \theta =\frac{2\,({{g}_{1}}{{g}_{2}}+{{f}_{1}}{{f}_{2}})-({{c}_{1}}+{{c}_{2}})}{2\sqrt{g_{1}^{2}+f_{1}^{2}-{{c}_{1}}}\,\,\sqrt{g_{2}^{2}+f_{2}^{2}-{{c}_{2}}}}\].
If \[S\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\]
\[S'\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\]
are two circles with radii \[{{r}_{1}},\,\,{{r}_{2}}\] and d be the distance between their centres then the angle of intersection \[\theta \] between them is given by \[\cos \theta =\frac{r_{1}^{2}+r_{2}^{2}-{{d}^{2}}}{2{{r}_{1}}{{r}_{2}}}\] or \[\cos \theta =\frac{2\,({{g}_{1}}{{g}_{2}}+{{f}_{1}}{{f}_{2}})-({{c}_{1}}+{{c}_{2}})}{2\sqrt{g_{1}^{2}+f_{1}^{2}-{{c}_{1}}}\,\,\sqrt{g_{2}^{2}+f_{2}^{2}-{{c}_{2}}}}\].
 Condition of Orthogonality : If the angle of intersection of the two circles is a right angle \[(\theta ={{90}^{o}})\], then such circles are called orthogonal circles and condition for orthogonality is \[2{{g}_{1}}{{g}_{2}}+2{{f}_{1}}{{f}_{2}}={{c}_{1}}+{{c}_{2}}\].
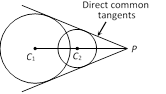
Condition of Orthogonality : If the angle of intersection of the two circles is a right angle \[(\theta ={{90}^{o}})\], then such circles are called orthogonal circles and condition for orthogonality is \[2{{g}_{1}}{{g}_{2}}+2{{f}_{1}}{{f}_{2}}={{c}_{1}}+{{c}_{2}}\].  In this case four common tangents can be drawn to the two circles, in which two are direct common tangents and the other two are transverse common tangents.
The points P, T of intersection of direct common tangents and transverse common tangents respectively, always lie on the line joining the centres of the two circles and divide it externally and internally respectively in the ratio of their radii.
\[\frac{{{C}_{1}}P}{{{C}_{2}}P}=\frac{{{r}_{1}}}{{{r}_{2}}}\](externally) and \[\frac{{{C}_{1}}T}{{{C}_{2}}T}=\frac{{{r}_{1}}}{{{r}_{2}}}\](internally)
Hence, the ordinates of P and T are
\[P\equiv \left( \frac{{{r}_{1}}{{x}_{2}}-{{r}_{2}}{{x}_{1}}}{{{r}_{1}}-{{r}_{2}}},\frac{{{r}_{1}}{{y}_{2}}-{{r}_{2}}{{y}_{1}}}{{{r}_{1}}-{{r}_{2}}} \right)\]and\[T\equiv \left( \frac{{{r}_{1}}{{x}_{2}}+{{r}_{2}}{{x}_{1}}}{{{r}_{1}}+{{r}_{2}}},\frac{{{r}_{1}}{{y}_{2}}+{{r}_{2}}{{y}_{1}}}{{{r}_{1}}+{{r}_{2}}} \right)\].
Case II : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,=\,{{r}_{1}}+{{r}_{2}}\] i.e., the distance between the centres is equal to the sum of radii.
In this case four common tangents can be drawn to the two circles, in which two are direct common tangents and the other two are transverse common tangents.
The points P, T of intersection of direct common tangents and transverse common tangents respectively, always lie on the line joining the centres of the two circles and divide it externally and internally respectively in the ratio of their radii.
\[\frac{{{C}_{1}}P}{{{C}_{2}}P}=\frac{{{r}_{1}}}{{{r}_{2}}}\](externally) and \[\frac{{{C}_{1}}T}{{{C}_{2}}T}=\frac{{{r}_{1}}}{{{r}_{2}}}\](internally)
Hence, the ordinates of P and T are
\[P\equiv \left( \frac{{{r}_{1}}{{x}_{2}}-{{r}_{2}}{{x}_{1}}}{{{r}_{1}}-{{r}_{2}}},\frac{{{r}_{1}}{{y}_{2}}-{{r}_{2}}{{y}_{1}}}{{{r}_{1}}-{{r}_{2}}} \right)\]and\[T\equiv \left( \frac{{{r}_{1}}{{x}_{2}}+{{r}_{2}}{{x}_{1}}}{{{r}_{1}}+{{r}_{2}}},\frac{{{r}_{1}}{{y}_{2}}+{{r}_{2}}{{y}_{1}}}{{{r}_{1}}+{{r}_{2}}} \right)\].
Case II : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,=\,{{r}_{1}}+{{r}_{2}}\] i.e., the distance between the centres is equal to the sum of radii.
 In this case two direct common tangents are real and distinct while the transverse tangents are coincident.
Case III : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,<\,{{r}_{1}}+{{r}_{2}}\] i.e., the distance between the centres is less than sum of radii.
In this case two direct common tangents are real and distinct while the transverse tangents are coincident.
Case III : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,<\,{{r}_{1}}+{{r}_{2}}\] i.e., the distance between the centres is less than sum of radii.
 In this case two direct common tangents are real and distinct while the transverse tangents are imaginary.
Case IV : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,=\,\,|\,{{r}_{1}}-{{r}_{2}}\,|\,\,,\] i.e., the distance between the centres is equal to the difference of the radii.
In this case two direct common tangents are real and distinct while the transverse tangents are imaginary.
Case IV : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,=\,\,|\,{{r}_{1}}-{{r}_{2}}\,|\,\,,\] i.e., the distance between the centres is equal to the difference of the radii.
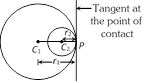 In this case two tangents are real and coincident while the other two tangents are imaginary.
Case V : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,<\,\,|\,{{r}_{1}}-{{r}_{2}}\,|\,\,,\] i.e., the distance between the centres is less than the difference of the radii.
In this case two tangents are real and coincident while the other two tangents are imaginary.
Case V : When \[|\,{{C}_{1}}{{C}_{2}}\,|\,<\,\,|\,{{r}_{1}}-{{r}_{2}}\,|\,\,,\] i.e., the distance between the centres is less than the difference of the radii.
 In this case, all the four common tangents are imaginary.
In this case, all the four common tangents are imaginary. 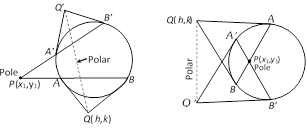 Equation of polar of the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] w.r.t. \[({{x}_{1}},{{y}_{1}})\] is \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
If the circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\], then its polar w.r.t. \[({{x}_{1}},{{y}_{1}})\]is \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\].
The pole of the line \[lx+my+n=0\] with respect to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]. Let pole be \[({{x}_{1}},\,{{y}_{1}}),\] then equation of polar with respect to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\], which is same as \[lx+my+n=0\]
Then \[\frac{{{x}_{1}}}{l}=\frac{{{y}_{1}}}{m}=-\frac{{{a}^{2}}}{n}\], \[\therefore \] \[{{x}_{1}}=-\frac{{{a}^{2}}l}{n}\] and \[{{y}_{1}}=-\frac{{{a}^{2}}m}{n}\].
Hence, the required pole is \[\left( -\frac{{{a}^{2}}l}{n},-\frac{{{a}^{2}}m}{n} \right)\].
Properties of pole and polar
(i) If the polar of \[P\,({{x}_{1}},\,{{y}_{1}})\] w.r.t. a circle passes through \[Q\,({{x}_{2}},\,{{y}_{2}})\] then the polar of Q will pass through P and such points are said to be conjugate points.
(ii) If the pole of the line \[ax+by+c=0\] w.r.t. a circle lies on another line \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0;\] then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
Equation of polar of the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] w.r.t. \[({{x}_{1}},{{y}_{1}})\] is \[x{{x}_{1}}+y{{y}_{1}}+g(x+{{x}_{1}})+f(y+{{y}_{1}})+c=0\].
If the circle is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\], then its polar w.r.t. \[({{x}_{1}},{{y}_{1}})\]is \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\].
The pole of the line \[lx+my+n=0\] with respect to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]. Let pole be \[({{x}_{1}},\,{{y}_{1}}),\] then equation of polar with respect to the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x{{x}_{1}}+y{{y}_{1}}-{{a}^{2}}=0\], which is same as \[lx+my+n=0\]
Then \[\frac{{{x}_{1}}}{l}=\frac{{{y}_{1}}}{m}=-\frac{{{a}^{2}}}{n}\], \[\therefore \] \[{{x}_{1}}=-\frac{{{a}^{2}}l}{n}\] and \[{{y}_{1}}=-\frac{{{a}^{2}}m}{n}\].
Hence, the required pole is \[\left( -\frac{{{a}^{2}}l}{n},-\frac{{{a}^{2}}m}{n} \right)\].
Properties of pole and polar
(i) If the polar of \[P\,({{x}_{1}},\,{{y}_{1}})\] w.r.t. a circle passes through \[Q\,({{x}_{2}},\,{{y}_{2}})\] then the polar of Q will pass through P and such points are said to be conjugate points.
(ii) If the pole of the line \[ax+by+c=0\] w.r.t. a circle lies on another line \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0;\] then the pole of the second line will lie on the first and such lines are said to be conjugate lines. 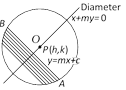 The equation of the diameter bisecting parallel chords \[y=mx+c\] (c is a parameter) of the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x+my=0.\]
The equation of the diameter bisecting parallel chords \[y=mx+c\] (c is a parameter) of the circle \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is \[x+my=0.\]
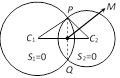 \[{{S}_{1}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\] ….(i)
and \[{{S}_{2}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\] ….(ii)
is \[2x\,({{g}_{1}}-{{g}_{2}})+2y\,({{f}_{1}}-{{f}_{2}})+{{c}_{1}}-{{c}_{2}}=0\] i.e., \[{{S}_{1}}-{{S}_{2}}=0\].
(3) Length of the common chord :
\[PQ=2\,(PM)=2\,\sqrt{{{C}_{1}}{{P}^{2}}-{{C}_{1}}{{M}^{2}}}\]
Where \[{{C}_{1}}P=\] radius of the circle \[{{S}_{1}}=0\] and \[{{C}_{1}}M=\] length of the perpendicular from the centre \[{{C}_{1}}\] to the common chord PQ.
\[{{S}_{1}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0\] ….(i)
and \[{{S}_{2}}\equiv {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0\] ….(ii)
is \[2x\,({{g}_{1}}-{{g}_{2}})+2y\,({{f}_{1}}-{{f}_{2}})+{{c}_{1}}-{{c}_{2}}=0\] i.e., \[{{S}_{1}}-{{S}_{2}}=0\].
(3) Length of the common chord :
\[PQ=2\,(PM)=2\,\sqrt{{{C}_{1}}{{P}^{2}}-{{C}_{1}}{{M}^{2}}}\]
Where \[{{C}_{1}}P=\] radius of the circle \[{{S}_{1}}=0\] and \[{{C}_{1}}M=\] length of the perpendicular from the centre \[{{C}_{1}}\] to the common chord PQ. You need to login to perform this action.
You will be redirected in
3 sec
