 where,\[S=\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}-1\],\[{{S}_{1}}=\frac{x_{1}^{2}}{{{a}^{2}}}-\frac{y_{1}^{2}}{{{b}^{2}}}-1,\,T=\frac{x{{x}_{1}}}{{{a}^{2}}}-\frac{y{{y}_{1}}}{{{b}^{2}}}-1\]
Director circle : The director circle is the locus of points from which perpendicular tangents are drawn to the given hyperbola. The equation of the director circle of the hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{b}^{2}}\].
where,\[S=\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}-1\],\[{{S}_{1}}=\frac{x_{1}^{2}}{{{a}^{2}}}-\frac{y_{1}^{2}}{{{b}^{2}}}-1,\,T=\frac{x{{x}_{1}}}{{{a}^{2}}}-\frac{y{{y}_{1}}}{{{b}^{2}}}-1\]
Director circle : The director circle is the locus of points from which perpendicular tangents are drawn to the given hyperbola. The equation of the director circle of the hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{b}^{2}}\]. 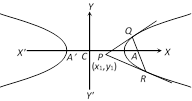
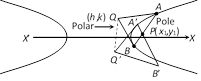
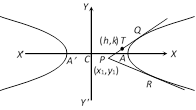
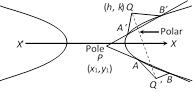 Pole of a given line: The pole of a given line \[lx+my+n=0\] with respect to the hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[({{x}_{1}},{{y}_{1}})=\]\[\left( -\frac{{{a}^{2}}l}{n},\,\frac{{{b}^{2}}m}{n} \right)\].
Properties of pole and polar
(i) If the polar of \[P({{x}_{1}},\,{{y}_{1}})\] passes through \[{{y}_{1}},{{y}_{2}},\,{{y}_{3}}\], then the polar of \[Q({{x}_{2}},{{y}_{2}})\] goes through \[P({{x}_{1}},\,{{y}_{1}})\] and such points are said to be conjugate points.
(ii) If the pole of a line \[lx+my+n=0\] lies on the another line \[4{{x}^{2}}-(4h-k)\,x-1=0\] then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
(iii) Pole of a given line is same as point of intersection of tangents as its extremities.
Pole of a given line: The pole of a given line \[lx+my+n=0\] with respect to the hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] is \[({{x}_{1}},{{y}_{1}})=\]\[\left( -\frac{{{a}^{2}}l}{n},\,\frac{{{b}^{2}}m}{n} \right)\].
Properties of pole and polar
(i) If the polar of \[P({{x}_{1}},\,{{y}_{1}})\] passes through \[{{y}_{1}},{{y}_{2}},\,{{y}_{3}}\], then the polar of \[Q({{x}_{2}},{{y}_{2}})\] goes through \[P({{x}_{1}},\,{{y}_{1}})\] and such points are said to be conjugate points.
(ii) If the pole of a line \[lx+my+n=0\] lies on the another line \[4{{x}^{2}}-(4h-k)\,x-1=0\] then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
(iii) Pole of a given line is same as point of intersection of tangents as its extremities. 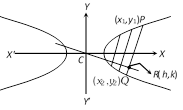 Let \[y=mx+c\] a system of parallel chords to \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] for different chords then the equation of diameter of the hyperbola is \[y=\frac{{{b}^{2}}x}{{{a}^{2}}m},\] which is passing through (0, 0).
Conjugate diameter : Two diameters are said to be conjugate when each bisects all chords parallel to the others.
If \[y={{m}_{1}}x,\,\,y={{m}_{2}}x\] be conjugate diameters, then \[{{m}_{1}}{{m}_{2}}=\frac{{{b}^{2}}}{{{a}^{2}}}\].
Let \[y=mx+c\] a system of parallel chords to \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] for different chords then the equation of diameter of the hyperbola is \[y=\frac{{{b}^{2}}x}{{{a}^{2}}m},\] which is passing through (0, 0).
Conjugate diameter : Two diameters are said to be conjugate when each bisects all chords parallel to the others.
If \[y={{m}_{1}}x,\,\,y={{m}_{2}}x\] be conjugate diameters, then \[{{m}_{1}}{{m}_{2}}=\frac{{{b}^{2}}}{{{a}^{2}}}\]. 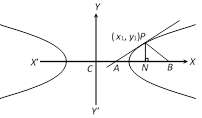 Length of subtangent
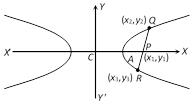
\[AN=CN-CA={{x}_{1}}-\frac{{{a}^{2}}}{{{x}_{1}}}\].
Length of subnormal
\[BN=CB-CN=\frac{({{a}^{2}}+{{b}^{2}})}{{{a}^{2}}}{{x}_{1}}-{{x}_{1}}\]
=\[\frac{{{b}^{2}}}{{{a}^{2}}}{{x}_{1}}=({{e}^{2}}-1){{x}_{1}}\].
Length of subtangent
\[AN=CN-CA={{x}_{1}}-\frac{{{a}^{2}}}{{{x}_{1}}}\].
Length of subnormal
\[BN=CB-CN=\frac{({{a}^{2}}+{{b}^{2}})}{{{a}^{2}}}{{x}_{1}}-{{x}_{1}}\]
=\[\frac{{{b}^{2}}}{{{a}^{2}}}{{x}_{1}}=({{e}^{2}}-1){{x}_{1}}\]. 
You need to login to perform this action.
You will be redirected in
3 sec
