Series
Learning Objectives
- Number Series
- Letter Series
- Mixed Series
Series
Series is a sequence of elements put together according to a certain rule. Series is mainly of three types - Letter Series, Number Series and Mixed Series.
Number Series
Such type of series consists of numbers that are arranged in a particular sequence, in the question related to number series, candidates are asked either to insert a missing number or find the one that does not follow the pattern of the series. On this basis we divided the questions of number series in two types.
Let’s discuss them one by one.
Type - I (To insert a missing number)
4, 9, 19, 34, 54, ?, 109
(a) 89 (b) 84
(c) 74 (d) 79
(e) None of these
Answer: (d)
Explanation: The difference between the numbers increases by 5 at each step as it means left to right in the series, after beginning from 5, i.e.,

27, 28, 25, 25, 23, 22, 21?
(a) 20 (b) 21
(c) 19 (d) 18
(e) None of these
Answer: (c)
Explanation: There are two alternate series:
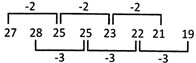
Series I: 27, 25, 23, 21 (following - 2 pattern)
Series II: 28, 25, 22, 19 (following - 3 pattern)
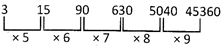
3, 15, 90, 630, 5040,?
(a) 35280 (b) 40320
(c) 45360 (d) 10080
(e) None of these
Answer: (c)
Explanation: The series follows the pattern given below.
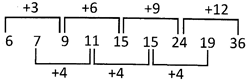
6, 7, 9, 11, 15, 15, 24, 19 ?
(a) 32 (b) 34
(c) 36 (d) 37
(e) None of these
Answer: (c)
Explanation: There are two alternate series.
Type - II (To find the number that does not follow the pattern of the series)
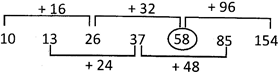
10, 13, 26, 37, 51, 85, 154
(a) 10 (b) 26
(c) 51 (d) 154
(e) None of these
Answer: (c)
Explanation: The given series contains two alternate series.
9, 13, 21, 37, 69, 132, 261?
(a) 21 (b) 37
(c) 69 (d) 132
(e) 261
Answer: (d)
Explanation:
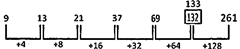
Hence, the wrong number is 132 and should be replaced by 133.
2, 5, 11, 23, 48, 95, 191, 383
(a) 5 (b) 11
(c) 23 (d) 48
(e) 95
Answer: (d)
Explanation:
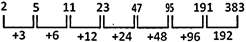
Hence, number 48 is wrong and
more...
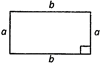
 Properties of a parallelogram
Properties of a parallelogram
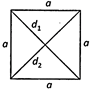
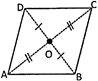 Properties of a Rhombus
Properties of a Rhombus