question_answer 1) A body cools down from\[80{}^\circ C\]to\[70{}^\circ C\]in 6 min. The time taken to cool it from\[60{}^\circ C\]to\[50{}^\circ C\]will be
A)
less than 6 min
done
clear
B)
6 min
done
clear
C)
more than 6 min
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 2) At temperature\[227{}^\circ C,\]the power radiated by a body is\[Q\text{ }cal/c{{m}^{^{2}}}\]. At the temperature\[727{}^\circ C\] the power radiated by it will be
A)
2Q
done
clear
B)
4 Q
done
clear
C)
16 Q
done
clear
D)
32 Q
done
clear
View Answer play_arrow
question_answer 3) A train of mass\[5\times {{10}^{6}}\]kg is moving with velocity 72 km/s. If it is sloped by applying break, then the value of heat generated will be
A)
\[1.2\times {{10}^{5}}k-cal\]
done
clear
B)
\[2.4\times {{10}^{5}}k-cal\]
done
clear
C)
\[4.8\times {{10}^{5}}k-cal\]
done
clear
D)
\[6\times {{10}^{5}}k-cal\]
done
clear
View Answer play_arrow
question_answer 4) For a gas, if ratio of specific heat is 7. If gas constant is R, then the value of specific heat at constant volume will be
A)
\[\frac{R}{(\gamma -1)}\]
done
clear
B)
\[\frac{R}{\gamma +1}\]
done
clear
C)
\[\frac{R}{\gamma }\]
done
clear
D)
\[R(\gamma -1)\]
done
clear
View Answer play_arrow
question_answer 5) The value of critical temperature in terms of van der Waal's constant a and b is
A)
\[1.2\,\times \,{{10}^{5}}k-cal\]
done
clear
B)
\[2.4\,\times \,{{10}^{5}}k-cal\]
done
clear
C)
\[4.8\,\times \,{{10}^{5}}k-cal\]
done
clear
D)
\[6\,\times \,{{10}^{5}}k-cal\]
done
clear
View Answer play_arrow
question_answer 6) The surface tension of a soap solution is\[2\times {{10}^{-2}}\]N/m. To blow a bubble of radius 2 cm from 1 cm, the work done is
A)
\[1.5\pi \times {{10}^{-4}}J\]
done
clear
B)
\[1.2\pi \times {{10}^{-4}}J\]
done
clear
C)
\[0.3\pi \times {{10}^{-4}}J\]
done
clear
D)
\[0.6\pi \times {{10}^{-4}}J\]
done
clear
View Answer play_arrow
question_answer 7) A second pendulum is taken in a satellite moving at a height of 2R from the earth's surface. At that position the time period (in second) of pendulum will be
A)
0
done
clear
B)
2
done
clear
C)
4
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 8) A space shuttle of mass 2500 kg is projected outside the gravitational field of the earth in space. The radius of earth is 6400 km. The minimum initial velocity of the shutle should be
A)
5.6 km/s
done
clear
B)
7.25 km/s
done
clear
C)
8.5 km/s
done
clear
D)
11.2 km/s
done
clear
View Answer play_arrow
question_answer 9) Where can a geostationary sattelite be placed?
A)
Above the city at equatorial
done
clear
B)
Above the north pole or south pole
done
clear
C)
In the orbit making\[23.5{}^\circ \]with equatorial plane
done
clear
D)
In the orbit making\[66.5{}^\circ \]with equatorial plane
done
clear
View Answer play_arrow
question_answer 10) \[n\] bullets of each of mass m hits the surface with velocity \[u\]. The force feet by surface will be
A)
\[mnu\]
done
clear
B)
\[2\text{ }mnu\]
done
clear
C)
\[4\text{ }mnu\]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 11) A particle is vibrating in a simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position, its energy half potential and half kinetic?
A)
\[2\sqrt{2}\,cm\]
done
clear
B)
\[2\,cm\]
done
clear
C)
\[\sqrt{2}\]
done
clear
D)
\[\frac{3}{\sqrt{2}}cm\]
done
clear
View Answer play_arrow
question_answer 12) Inertia of a thin rod of mass M and length L about an axis making an angle\[90{}^\circ \]with its length is \[\frac{M{{L}^{2}}}{9}.\] The distance of this axis from the midpoint of rod will be
A)
\[\frac{L}{6}\]
done
clear
B)
\[\frac{L}{3}\]
done
clear
C)
\[\frac{L}{4}\]
done
clear
D)
\[\frac{L}{2}\]
done
clear
View Answer play_arrow
question_answer 13) A ball at angle\[30{}^\circ \]with velocity v0 through in the vertically direction. Which statement will be true?
A)
Gravitational potential energy at maximum height of projectile path will be minimum
done
clear
B)
The kinetic energy of ball at maximum height of projectile path will be zero
done
clear
C)
The horizontal component of momentum will not change
done
clear
D)
The vertical component of momentum will not change
done
clear
View Answer play_arrow
question_answer 14) A body is rotating with angular velocity\[\overrightarrow{\omega }\]and its angular momentum is L, then relation between T and L will be
A)
\[\overset{\to }{\mathop{T}}\,=\,{{\omega }^{\to }}\times {{L}^{\to }}\]
done
clear
B)
\[{{L}^{\to }}=L\frac{\,\,\,{{\omega }^{\to }}}{dt}\]
done
clear
C)
\[{{T}^{\to }}={{\omega }^{\to }}\frac{\,\,\,d{{L}^{\to }}}{dt}\]
done
clear
D)
\[{{T}^{\to }}=\frac{\,\,\,d{{L}^{\to }}}{dt}\]
done
clear
View Answer play_arrow
question_answer 15)
Two masses of 4 kg and 5 kg are connected by a string passing through a frictionless pulley and are kept on a frictionless table as shown in the figure. The acceleration of 5 kg mass is
A)
\[49\text{ }m/{{s}^{2}}\]
done
clear
B)
\[5.44m/{{s}^{2}}\]
done
clear
C)
\[19.5\text{ }m/{{s}^{2}}\]
done
clear
D)
\[2.72\text{ }m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 16) The maximum angular displacement of simple pendulum of length\[l\]is\[\theta .\] Its maximum kinetic energy will be
A)
\[mgl\text{ }sin\theta \]
done
clear
B)
\[mgl\text{ }(1+sin\theta )\])
done
clear
C)
\[mgl(1+cos\theta )\]
done
clear
D)
\[mgl\text{ }(1-\cos \theta )\]
done
clear
View Answer play_arrow
question_answer 17) The height of water raised in capillary tube will be
A)
maximum at\[4{}^\circ C\]
done
clear
B)
maximum at \[0{}^\circ C\]
done
clear
C)
minimum at\[4{}^\circ C\]
done
clear
D)
minimum at\[0{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 18) The two gases\[{{O}_{2}}\]and\[{{H}_{2}}\]have same temperature at TK. Mean kinetic energy of molecules of\[{{O}_{2}}\] compare to mean kinetic energy of molecule of\[{{H}_{2}}\]will be
A)
16 times
done
clear
B)
8 times
done
clear
C)
equal
done
clear
D)
1/6 times
done
clear
View Answer play_arrow
question_answer 19) The relation between relative change of volume \[\left( \frac{\Delta V}{V} \right)\] and relative change of pressure \[\left( \frac{\Delta p}{p} \right)\] in adiabatic process is
A)
\[\frac{1}{\gamma }\left( \frac{\Delta V}{V} \right)\]
done
clear
B)
\[\frac{1}{{{\gamma }^{2}}}\left( \frac{\Delta V}{V} \right)\]
done
clear
C)
\[-\gamma \left( \frac{\Delta V}{V} \right)\]
done
clear
D)
\[\gamma \left( \frac{\Delta V}{V} \right)\]
done
clear
View Answer play_arrow
question_answer 20) An iron nail of 200 g is fitted in a wood piece with a speed of 50 m/s by a hammer of 1 kg. If specific heat of iron is\[0.105\text{ }cal/g{}^\circ C\]and half of the total energy given to nail is transfered in heat, then what will be the rise in temperature of nail?
A)
\[1.42{}^\circ C\]
done
clear
B)
\[9.2{}^\circ C\]
done
clear
C)
\[10.5{}^\circ C\]
done
clear
D)
\[12.1{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 21) There is a rough black spot on a polished metal plate. If the plate in heated up to\[1400{}^\circ C\]and taken in a dark room, then what will be the rise in temperature
A)
the spot will be brighter as compared to remaining part of plat.
done
clear
B)
spot and remaining part of the plate will be equally bright
done
clear
C)
Neither spot nor the remaining part of the plate will be bright
done
clear
D)
the spot is less bright, as compared to remaining part of the plate
done
clear
View Answer play_arrow
question_answer 22) The force due to surface tension of a capillary tube filled with water is balanced by the force of \[72\times {{10}^{-5}}\]N worked toward the base due to weight of water. The surface tension of water is 0.06 N/m. The internal radius of capillary tube will be will be
A)
0.5 mm
done
clear
B)
2 mm
done
clear
C)
1.1 mm
done
clear
D)
1.75 mm
done
clear
View Answer play_arrow
question_answer 23) The mass and radius of a planet have half the value of corresponding parameter of earth. Acceleration due to gravity on the surface the planet is
A)
\[4.9\text{ }m/{{s}^{2}}\]
done
clear
B)
\[9.8\text{ }m/{{s}^{2}}\]
done
clear
C)
\[19.6\text{ }m/{{s}^{2}}\]
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 24) The time period of satellites nearing the planet of radius R is T. Find the time period of nearest satellite for planet of radius 3R.
A)
\[3\sqrt{3}\,T\]
done
clear
B)
\[\frac{\sqrt{3}}{2}\,T\]
done
clear
C)
\[\frac{1}{3\sqrt{3}}\,T\]
done
clear
D)
\[\frac{3}{2}T\]
done
clear
View Answer play_arrow
question_answer 25) A body of mass m is taken from earth surface to the height A equal to radius of earth, the increase in potential energy will be
A)
\[\frac{mgR}{2}\]
done
clear
B)
\[mgR\]
done
clear
C)
\[2mgR\]
done
clear
D)
\[\frac{1}{4}mgR\]
done
clear
View Answer play_arrow
question_answer 26) When a mass 5 kg attached to a spring, it normally extends by 12 cm. If the weighted spring oscillates, then its time period will be
A)
0.7 s
done
clear
B)
0.9 s
done
clear
C)
1.1 s
done
clear
D)
1.4 s
done
clear
View Answer play_arrow
question_answer 27) The average kinetic energy of helium atom at\[30{}^\circ C\]will be
A)
13.6 eV
done
clear
B)
59.60 eV
done
clear
C)
15 keV
done
clear
D)
less from 1 eV
done
clear
View Answer play_arrow
question_answer 28) Star A has radius r, surface temperature T while star B has radius 4r and surface \[\frac{T}{2}\] temperature. The ratio of radiated power \[{{P}_{A}}\,:\,{{P}_{B}}\]from, then will be
A)
1 : 4
done
clear
B)
16 : 1
done
clear
C)
1 : 16
done
clear
D)
1 : 1
done
clear
View Answer play_arrow
question_answer 29) A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity \[\omega \]. Two objects each of mass m, are kept gently to the opposite ends of two perpendicular diameter of the ring. The angular velocity of the ring will be
A)
\[\frac{M\omega }{2m}\]
done
clear
B)
\[\frac{2M\omega }{M}\]
done
clear
C)
\[\frac{(M+2m)}{M}\omega \]
done
clear
D)
\[\left( \frac{M\omega }{M+2\omega } \right)\]
done
clear
View Answer play_arrow
question_answer 30) A fan of moment of inertia\[0.6\text{ }kg-{{m}^{2}}\]is turned upto a working speed of 0.5 rev/s. The angular momentum of the fan is
A)
\[0.3\pi \,kg-{{m}^{2}}/s\]
done
clear
B)
\[0.6\pi \,kg-{{m}^{2}}/s\]
done
clear
C)
\[\frac{0.03}{\pi }\,kg-{{m}^{2}}/s\]
done
clear
D)
\[\frac{0.6}{\pi }\,kg-{{m}^{2}}/s\]
done
clear
View Answer play_arrow
question_answer 31) In an AC circuit L is 0.5 H and C is 8\[\mu \]F. In circuit for maximum current, angular frequency will be
A)
500 rad/s
done
clear
B)
250 rad/s
done
clear
C)
150 rad/s
done
clear
D)
100 rad/s
done
clear
View Answer play_arrow
question_answer 32) When 4 A current flows in a motor, the power loss in 20 W and the resultant potential difference is 220 V, emf will be
A)
220 V
done
clear
B)
225 V
done
clear
C)
240 V
done
clear
D)
260 V
done
clear
View Answer play_arrow
question_answer 33) A step up transformer operates on a 230 V line and supplies a load of 2 A. The ratio of the primary and secondary winding is 1 : 25. The current in the primary is
A)
50 A
done
clear
B)
25 A
done
clear
C)
12.5 A
done
clear
D)
6.25 A
done
clear
View Answer play_arrow
question_answer 34) The magnetic field at the rate of 0.4 T/s changes in perpendicular direction from square coil of an arm 4 cm. If the resistance of coil is \[2\times {{10}^{-3}}\Omega ,\] then induced current will be
A)
0.16 A
done
clear
B)
0.32 A
done
clear
C)
3.2 A
done
clear
D)
1.6 A
done
clear
View Answer play_arrow
question_answer 35) A magnet has length 0.2 m and its placed at angle \[30{}^\circ \]in magnetic field of\[30\text{ }Wb/{{m}^{2}}\]
A)
\[7.5\times {{10}^{-4}}N-m\]
done
clear
B)
\[3.0\times {{10}^{-4}}N-m\]
done
clear
C)
\[1.5\times {{10}^{-4}}N-m\]
done
clear
D)
\[6.0\times {{10}^{-4}}N-m\]
done
clear
View Answer play_arrow
question_answer 36) The atomic mass of ionic lithium atoms are 0.06 amu. If they are motion with energy 400 eV in magnetic field of 0.08 T, then radius of circular path will be
A)
8.83 cm
done
clear
B)
9.23 cm
done
clear
C)
10.5 cm
done
clear
D)
11.25 cm
done
clear
View Answer play_arrow
question_answer 37) In Young's double slit experiment, distance between two sources is 0.1 mm. The distance of screen from the sources is 20 cm. Wavelength of light used is 5460\[\overset{o}{\mathop{\text{A}}}\,\]. The distance between maxima will be
A)
0.5 mm
done
clear
B)
1.1 mm
done
clear
C)
1.5 mm
done
clear
D)
2.2 mm
done
clear
View Answer play_arrow
question_answer 38) The ratio of gravitational and electric forces between two electrons.
A)
\[{{10}^{-36}}\]
done
clear
B)
\[{{10}^{-39}}\]
done
clear
C)
\[{{10}^{-42}}\]
done
clear
D)
\[{{10}^{-47}}\]
done
clear
View Answer play_arrow
question_answer 39) Two charges \[4q\] and \[q\] are placed at distance\[l\]. In the middle adjoining line a charge\[Q\]is kept. If resultant force on \[q\] will be zero, then \[Q\] will be
A)
\[+q\]
done
clear
B)
\[-q\]
done
clear
C)
\[+2q\]
done
clear
D)
\[-2g\]
done
clear
View Answer play_arrow
question_answer 40) Suppose the electrical potential at any point is V, then electric field at that point along\[x-\]axis will be
A)
\[{{\int }^{\infty }}{{\,}_{0}}V\,dt\]
done
clear
B)
\[\frac{dV}{dx}\]
done
clear
C)
\[-\frac{dV}{dx}\]
done
clear
D)
\[-V\frac{dV}{dx}\]
done
clear
View Answer play_arrow
question_answer 41) The magnitude of charges in an electric dipole are \[3.2\times {{10}^{-19}}C\]and the distance between them is 2.4\[\overset{o}{\mathop{\text{A}}}\,\]. If its placed at the electric field of intensity \[4\times {{10}^{5}}\]V/m, then the electric dipole moment will be
A)
\[9.6\times {{10}^{-5}}C-m\]
done
clear
B)
\[12.8\times {{10}^{-14}}C-m\]
done
clear
C)
\[7.68\times {{10}^{-29}}C-m\]
done
clear
D)
\[30\times {{10}^{-24}}C-m\]
done
clear
View Answer play_arrow
question_answer 42) A helium nucleus makes a full rotation in a circle of radius 0.8 m in 2s. The value of the magnetic field at the centre of the circle will be
A)
\[{{\mu }_{0}}\,\times \,{{10}^{-19}}\,T\]
done
clear
B)
\[1.6\,\times {{\mu }_{0}}\,\times \,{{10}^{-19}}\,T\]
done
clear
C)
\[3{{\mu }_{0}}\,\times \,{{10}^{-19}}\,T\]
done
clear
D)
\[2{{\mu }_{0}}\,\times \,{{10}^{-19}}\,T\]
done
clear
View Answer play_arrow
question_answer 43)
A sinusoidal voltage of peak value 200 V is connected to a diode and capacitance C in the circuit shown, so that half wave rectification occurs.
A)
500 V
done
clear
B)
200 V
done
clear
C)
283 V
done
clear
D)
141 V
done
clear
View Answer play_arrow
question_answer 44) The ratio of energies of photon of wavelength 6000\[\overset{o}{\mathop{\text{A}}}\,\] to wavelength 4000\[\overset{o}{\mathop{\text{A}}}\,\]
A)
2 : 3
done
clear
B)
3 : 2
done
clear
C)
1 : 5
done
clear
D)
5 : 1
done
clear
View Answer play_arrow
question_answer 45) The third harmonic of a closed organ pipe is in resonance with the fourth overtone of open organ pipe. The ratio of lengths of the pipes is
A)
\[\frac{8}{7}\]
done
clear
B)
\[\frac{7}{8}\]
done
clear
C)
\[\frac{3}{5}\]
done
clear
D)
\[\frac{5}{3}\]
done
clear
View Answer play_arrow
question_answer 46) Two coherent monochromatic light beam of intensities \[I\] and \[4I\] are superposed. The maximum and minimum possible intensities in the resulting beam are
A)
\[3I\] and \[2I\]
done
clear
B)
\[25I\text{ }and\text{ }9I\]
done
clear
C)
\[9I\text{ }and\,I\]
done
clear
D)
\[5I\text{ }and\text{ }3I\]
done
clear
View Answer play_arrow
question_answer 47) Two steady sound sources having same frequency are placed at a distance of 1 m. An observer is moving at a distance of 10 m along the line joining there source. If the observed distance between first two successive maxima is 0.11 m, then frequency of sources is (velocity of sound v = 330 m/s.)
A)
1000 Hz
done
clear
B)
3000 Hz
done
clear
C)
3500 Hz
done
clear
D)
4000 Hz
done
clear
View Answer play_arrow
question_answer 48) A car moving with a speed of 28 m/s and blowing the horn of 500 Hz frequency waves another car moving at 15 m/s. What will be the observed frequency is the dimer of second car? (speed of sound = 332 m/s)
A)
480 Hz
done
clear
B)
500 Hz
done
clear
C)
520 Hz
done
clear
D)
580 Hz
done
clear
View Answer play_arrow
question_answer 49) The average emf induced in a coil in which current changes from 2 A to 4 A in 0.05 s is 8 V. What is the self inductance of the coil?
A)
0.5 H
done
clear
B)
0.35 H
done
clear
C)
0.2 H
done
clear
D)
2 mH
done
clear
View Answer play_arrow
question_answer 50) In a potential meter, a voltage source and battery of 3 V are balance at length 60cm length 45 cm respectively. The emf unknown voltage will be
A)
3 V
done
clear
B)
4 V
done
clear
C)
4.5 V
done
clear
D)
6 V
done
clear
View Answer play_arrow
question_answer 51) The square coil of turn 60 has length 20 cm and breath 10 cm is rotating rate of 1800 rev/min in uniform magnetic field of intensity 0.5 T. the maximum emf of coil will be
A)
98 V
done
clear
B)
110 V
done
clear
C)
113 V
done
clear
D)
118 V
done
clear
View Answer play_arrow
question_answer 52) The number of turn in the primary coil of a transformer is 240. For an input of alternating voltage 20 V, output voltage is 2.5 V. 7 number of turns in the secondary coil is
A)
250
done
clear
B)
100
done
clear
C)
10
done
clear
D)
30
done
clear
View Answer play_arrow
question_answer 53) A light wave is moving along y-axis. If \[E\to \] at a time along the x-axis, then direction of \[B\to \] at that time will along
A)
\[y-\]axis
done
clear
B)
\[x-\]axis
done
clear
C)
\[\text{+ }z-\]axis
done
clear
D)
\[-\text{ }z-\]axis
done
clear
View Answer play_arrow
question_answer 54) The current of an AC circuit is \[I=2\text{ }cos\] \[(\omega t\,+\,\theta ),\]then\[{{I}_{rms}}\]
A)
\[\sqrt{2}A\]
done
clear
B)
\[\frac{1}{\sqrt{2}}\,A\]
done
clear
C)
\[2A\]
done
clear
D)
\[\frac{1}{2}\,A\]
done
clear
View Answer play_arrow
question_answer 55) The intensity of magnetic field of a current carrying circular at a point on its axis at distance \[x(x>>R)\]will depends upon
A)
\[B\alpha \frac{1}{{{x}^{3/2}}}\]
done
clear
B)
\[B\alpha \frac{1}{{{x}^{2}}}\]
done
clear
C)
\[B\alpha \frac{1}{{{x}^{3}}}\]
done
clear
D)
\[B\alpha \frac{1}{{{x}^{1/2}}}\]
done
clear
View Answer play_arrow
question_answer 56) A given charge is situated at a certain distance from an electric dipole in the end on position experience a force F. If the distance of the charge is doubled, the force acting on the charge will be
A)
zero
done
clear
B)
\[F/2\]
done
clear
C)
\[F/4\]
done
clear
D)
\[F/8\]
done
clear
View Answer play_arrow
question_answer 57) In dielectric medium, the electric field is \[E\to \]. If permittivity of vacuum is \[{{\varepsilon }_{0}},\]then
A)
\[\frac{kE\to }{{{\varepsilon }_{0}}}\]
done
clear
B)
\[\frac{E\to }{K{{\varepsilon }_{0}}}\]
done
clear
C)
\[\frac{{{\varepsilon }_{0}}E\to }{k}\]
done
clear
D)
\[k{{\varepsilon }_{0}}E\to \]
done
clear
View Answer play_arrow
question_answer 58) The work done to complete one revolution in a circle of radius r by a charge Q, if a charge Q is placed at the centre of the circle will be
A)
\[\frac{Q}{4\pi {{\varepsilon }_{0}}r}\]
done
clear
B)
\[\frac{{{Q}^{2}}al}{4\pi {{\varepsilon }_{0}}r}\]
done
clear
C)
zero
done
clear
D)
\[\frac{Qal}{2r}\]
done
clear
View Answer play_arrow
question_answer 59) Two mirror are bended on each other in such a manner that the incident ray on first mirror, parallel to the second mirror, becomes parallel to first mirror by reflection through second mirror, then the angle between the two mirrors is
A)
\[30{}^\circ \]
done
clear
B)
\[45{}^\circ \]
done
clear
C)
\[60{}^\circ \]
done
clear
D)
\[75{}^\circ \]
done
clear
View Answer play_arrow
question_answer 60) The energy for ion on of a excited hydrogen atom is
A)
13.6
done
clear
B)
3.4
done
clear
C)
more than 13.6
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 61) The thickness of glass strip is t and refractive index n. If velocity of light in vacuum is c, then minimum time in cross the strip by light will be
A)
\[\frac{ct}{n}\]
done
clear
B)
\[\frac{nt}{c}\]
done
clear
C)
\[nct\]
done
clear
D)
\[\frac{nc}{t}\]
done
clear
View Answer play_arrow
question_answer 62) Some point in progressive waves are
A)
not remain at rest
done
clear
B)
always move
done
clear
C)
in each cycle two times at rest at the same time
done
clear
D)
in each cycle one time at rest at the same time
done
clear
View Answer play_arrow
question_answer 63) One end closed pipe of length L resonented at any frequency. The length of open both ends pipe, for resonant at same frequency will be
A)
L/2
done
clear
B)
L
done
clear
C)
3L/2
done
clear
D)
2L
done
clear
View Answer play_arrow
question_answer 64) The frequency of Piano of length 1.1 m and of mass 160 g is 33 Hz, the tension will be
A)
556 N
done
clear
B)
3000 N
done
clear
C)
843 N
done
clear
D)
995 N
done
clear
View Answer play_arrow
question_answer 65) A tuning forks gives 5 beats/s with 20 cm length of sonometer. If length of wire changes from 20 to 21, and not change in frequency, then frequency of tuning forks will be
A)
205 Hz
done
clear
B)
210 Hz
done
clear
C)
220 Hz
done
clear
D)
195 Hz
done
clear
View Answer play_arrow
question_answer 66) When semiconductor makes from Germanium doped by phosphorus, then in semiconductor
A)
quantity of negative electric charge will be maximum
done
clear
B)
electrons will be maximum
done
clear
C)
quantity of positive electric charge will be maximum
done
clear
D)
holes will be maximum
done
clear
View Answer play_arrow
question_answer 67) Two coils have a same centre, when the mutual inductance of both coil will be maximum, then axis of both will
A)
perpendicular
done
clear
B)
make an angle\[45{}^\circ \]
done
clear
C)
make an angle\[60{}^\circ \]
done
clear
D)
parallel
done
clear
View Answer play_arrow
question_answer 68) In insulator, energy interval of low order is
A)
zero
done
clear
B)
0.7 eV
done
clear
C)
1.1 eV
done
clear
D)
5 eV
done
clear
View Answer play_arrow
question_answer 69) In triode 8 amplifier voltage gain depends upon
A)
\[\mu ,\,{{R}_{L}}\,and\,input\,voltage\]
done
clear
B)
\[{{R}_{p}},{{R}_{L}}\]and\[\mu \]
done
clear
C)
\[\mu ,{{R}_{p}}\]and input voltage
done
clear
D)
\[{{R}_{p}},\mu \]and\[{{g}_{m}}\]
done
clear
View Answer play_arrow
question_answer 70) In hydrogen atom, the kinetic energy of moving electron in Bhor orbit of radius r will be
A)
\[Ke/2r\]
done
clear
B)
\[\frac{K{{e}^{2}}}{2r}\]
done
clear
C)
\[Ke/r\]
done
clear
D)
\[2Ke/4\]
done
clear
View Answer play_arrow
question_answer 71) A hydrogen atom is in first excited state, then ion energy will be
A)
13.1 eV
done
clear
B)
3.4 eV
done
clear
C)
1.51 eV
done
clear
D)
1.9 eV
done
clear
View Answer play_arrow
question_answer 72) An electron and positron have the same rest mass of 0.51 MeV. Find the wavelength of \[\gamma \] rays produced due to their fusion
A)
6.012\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
0.024\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
0.012 to\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
0.024 to\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 73) Crod makes of soft iron in electromagnet, because its
A)
diathesis and retantivity are maximum
done
clear
B)
diathesis is maximum and retantivity is minimum
done
clear
C)
diathesis and retantivity are minimum
done
clear
D)
retantivity is maximum and diathesis is minimum
done
clear
View Answer play_arrow
question_answer 74) A converging lens is used to form an image on a screen. When half of the lens is covered by opaque screen.
A)
Half the image will disappear
done
clear
B)
Upper half the image will disappear
done
clear
C)
Complete image will be formed of decreased intensity
done
clear
D)
Complete image will disappear
done
clear
View Answer play_arrow
question_answer 75) In an X-rays tube, the electron accelerated by potential V volt, the minimum wavelength of X-rays will be
A)
\[\frac{2400}{V}\]\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
\[\frac{12400}{V}\]\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
\[\frac{12.4}{V}\]\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
\[\frac{V}{124000}\]\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 76) The atomic weight of boran is 10.81 and it has two isotopes \[_{5}{{\beta }^{10}}\] and \[_{5}{{\beta }^{11}}\]. Then ratio of \[_{5}{{\beta }^{10}}\]: \[_{5}{{\beta }^{11}}\] in nature would be
A)
19 : 81
done
clear
B)
10 : 11
done
clear
C)
15 : 61
done
clear
D)
81 : 19
done
clear
View Answer play_arrow
question_answer 77) A galvanometer of\[10\,\Omega \]resistance gives full scale deflection with 0.01 A of current. It is to be converted into an ammeter for measuring 10 A current. The value of shunt resistance will be
A)
\[11\,\Omega \]resistance in series
done
clear
B)
100 resistance in series
done
clear
C)
990\[\Omega \] resistance in series
done
clear
D)
0.10\[\Omega \] resistance in series
done
clear
View Answer play_arrow
question_answer 78) Half year of a radioactive element is 5 days. The time during which quantity remains 7/8 of initial mass will be
A)
2, 5 days
done
clear
B)
5 days
done
clear
C)
10 days
done
clear
D)
15 days
done
clear
View Answer play_arrow
question_answer 79) When a choke coil of resistance zero works at 200 V, then the 5 mA current flows its. The power in choke coil is
A)
zero
done
clear
B)
11 W
done
clear
C)
\[44\times {{10}^{3}}W\]
done
clear
D)
1.1 W
done
clear
View Answer play_arrow
question_answer 80)
The below diagram shows a parabola. Its physical quantities and y at constant acceleration represent respectively
A)
X = time, Y = velocity
done
clear
B)
X = time, Y = displacement
done
clear
C)
X = time, Y = acceleration
done
clear
D)
X = velocity, Y = displacement
done
clear
View Answer play_arrow
question_answer 81) The chemical equivalent of silver is 108. If the current in silver voltameter is 2 A; then the during time in collecting of 27 g silver will be
A)
8.75 h
done
clear
B)
6.70 h
done
clear
C)
3.35 h
done
clear
D)
12.50 h
done
clear
View Answer play_arrow
question_answer 82) The reactance of a coil at frequency 50 Hz is 1000, the reactance at frequency 100 Hz will be
A)
100\[\Omega \]
done
clear
B)
300\[\Omega \]
done
clear
C)
450\[\Omega \]
done
clear
D)
600\[\Omega \]
done
clear
View Answer play_arrow
question_answer 83) For iron magnet materials
A)
permeability is high and tendency is positive and low
done
clear
B)
permeability is very high and tendency is negative and low
done
clear
C)
permeability is very low and tendency is positive and high
done
clear
D)
permeability is very low and tendency is negative and low
done
clear
View Answer play_arrow
question_answer 84) The magnetic susceptibility of any paramagnetic material changes with absolute temperature T as
A)
\[\chi \,\alpha \,T\]
done
clear
B)
\[\chi \,\alpha \,\frac{1}{T}\]
done
clear
C)
\[\chi \,\alpha \,\frac{1}{(1-T)}\]
done
clear
D)
constant
done
clear
View Answer play_arrow
question_answer 85) The grid voltage of any triode valve is changed from\[-2.5\text{ }V\]to\[-4.5\text{ }V\]and the mutual conductance is\[8\times {{10}^{-4}}\]mho. The change in plate circuit current will be
A)
\[1.6\times {{10}^{-3}}A\]
done
clear
B)
\[2.0\times {{10}^{-4}}A\]
done
clear
C)
\[1.6\times {{10}^{-3}}A\]
done
clear
D)
\[1.6\times {{10}^{-4}}A\]
done
clear
View Answer play_arrow
question_answer 86) To obtain a P-type germanium semiconductor, it must be doped with
A)
boran
done
clear
B)
antimany
done
clear
C)
arsenic
done
clear
D)
phosphorus
done
clear
View Answer play_arrow
question_answer 87) In a triode amplifier,\[\mu =25,\]\[{{r}_{p}}=40\text{ }k\Omega \] and load resistance\[{{R}_{L}}=10\text{ }k\Omega \]. If the input signal voltage is 0.5 V, then output signal voltage will be
A)
1.25 V
done
clear
B)
2.5 V
done
clear
C)
5 V
done
clear
D)
10 V
done
clear
View Answer play_arrow
question_answer 88) The radius of the coil of a tangent galvanometer which has 10 turn is 0.1 m. The current required to produce a deflection of \[60{}^\circ \] is
A)
\[3A\]
done
clear
B)
\[1.1A\]
done
clear
C)
\[2.1A\]
done
clear
D)
\[1.5A~\]
done
clear
View Answer play_arrow
question_answer 89) The atomic weight of thorium is 232 and atomic no Z = 90. Disintegration of thorium finally gives Pb for which A = 208 and Z = 82. For this process the number of \[\alpha \] and\[\beta \] particles respectively are
A)
4 and 6
done
clear
B)
6 and 4
done
clear
C)
3 and 2
done
clear
D)
2 and 3
done
clear
View Answer play_arrow
question_answer 90) The work function of metal is 2.4 eV. The maximum wavelength of photon for emitted the electric light will be
A)
3000\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
3500 \[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
4500 \[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
5156 \[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 91) The ratio of ioning power of\[\alpha \]and\[\beta \]particle emitted from a radioactive element will be
A)
1 : 100
done
clear
B)
100 : 1
done
clear
C)
1000 : 1
done
clear
D)
1 : 1000
done
clear
View Answer play_arrow
question_answer 92) The momentum of X-ray photon of wavelength 0.01\[\overset{o}{\mathop{\text{A}}}\,\]in kg-m/s will be
A)
\[6.6\times {{10}^{-21}}\]
done
clear
B)
\[6.6\times {{10}^{-32}}\]
done
clear
C)
\[6.6\times {{10}^{-46}}\]
done
clear
D)
\[6.6\times {{10}^{-22}}\]
done
clear
View Answer play_arrow
question_answer 93) The minimum wavelength of X-rays achive from the\[\alpha -\]ray tube is 0.1 A. The maximum voltage
A)
\[1.25\times {{10}^{3}}V\]
done
clear
B)
\[1.24\times {{10}^{4}}V\]
done
clear
C)
\[1.24\times {{10}^{5}}V\]
done
clear
D)
\[1.24\times {{10}^{6}}V\]
done
clear
View Answer play_arrow
question_answer 94) An electron is accelerated through a potential of 50000 V. Its de-Broglie wavelength of electron will be
A)
0.55\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
0.055\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
0.077\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
0.095\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 95) The wavelength of second line of Lyman series is 1025\[\overset{o}{\mathop{\text{A}}}\,\]. The wavelength of first line will be
A)
825\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
900\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
1215\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
1325\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 96) In hydrogen atom, the momentum of electron in second orbit of radius r will be
A)
\[\frac{h}{2\pi }\]
done
clear
B)
\[\frac{h}{\pi }\]
done
clear
C)
\[\frac{h}{\pi r}\]
done
clear
D)
\[\frac{h}{2\pi r}\]
done
clear
View Answer play_arrow
question_answer 97) An electric heater of resistance 70, heats 0.1 kg of water of\[20{}^\circ C\]for 3 min. If it carries a current of 4 A, then what will be the final temperature (specific heat of water\[=4.2\times {{10}^{3}}J/kg\text{ }K\])
A)
\[28{}^\circ C\]
done
clear
B)
\[48{}^\circ C\]
done
clear
C)
\[52{}^\circ C\]
done
clear
D)
\[68{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 98) In LCR circuit having C = 25\[\mu \]F, L = 02 H and R = 25\[\Omega \]. If a generator of E = 320 sin 314 t volt is connect in the circuit, then impedence will be
A)
57.320\[\Omega \]
done
clear
B)
79.480\[\Omega \]
done
clear
C)
89.50\[\Omega \]
done
clear
D)
99.10\[\Omega \]
done
clear
View Answer play_arrow
question_answer 99) In question 98, how much inductance is added the circuit so that reactance becomes minimum?
A)
0.31 H
done
clear
B)
0.41 H
done
clear
C)
1.25 H
done
clear
D)
1.75 H
done
clear
View Answer play_arrow
question_answer 100) In a circuit the current is given by\[I={{l}_{0}}sin\] \[(\omega t-\pi /2)\]and the potential is\[V={{V}_{0}}sin\] at, then
A)
\[\frac{1}{2}{{I}_{0}}{{e}_{0}}\,watt\]
done
clear
B)
\[{{I}_{0}}{{\varepsilon }_{0}}\,watt\]
done
clear
C)
\[{{I}_{0}}\,watt\]
done
clear
D)
\[zero\]
done
clear
View Answer play_arrow
question_answer 101) Which of the following has minimum energy?
A)
\[\sigma \]bond
done
clear
B)
\[\pi \]bond
done
clear
C)
ionic bond
done
clear
D)
hydrogen bond
done
clear
View Answer play_arrow
question_answer 102) The addition of a reagent to an unsymmetric alkene take place in such a way that the negative part of the reagent will be attached to the carbon atom which containing lesser number of H-atom. This statement belongs to
A)
Markownikoffs rule
done
clear
B)
Peroxide effect
done
clear
C)
Saytzeffs rule
done
clear
D)
Le-Chatelier's principle
done
clear
View Answer play_arrow
question_answer 103) The atomic mass of two elements is same. There are 27 protons in first element and 30 protons in second element. If 30 neutrons are present in first element then neutron in second element will be
A)
27
done
clear
B)
30
done
clear
C)
29
done
clear
D)
28
done
clear
View Answer play_arrow
question_answer 104) Which of the following alcohol will form the most stable carbonium ion on dehydration?
A)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{CH}}\,-C{{H}_{2}}OH\]
done
clear
B)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{\overset{\begin{smallmatrix} C{{H}_{3}} \\ | \end{smallmatrix}}{\mathop{C}}\,}}\,-OH\]
done
clear
C)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} | \\ OH \end{smallmatrix}}{\mathop{CH}}\,-C{{H}_{2}}C{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}C{{H}_{2}}C{{H}_{2}}OH\]
done
clear
View Answer play_arrow
question_answer 105) Which of the following is strong reducing agent?
A)
\[Li\]
done
clear
B)
\[Na\]
done
clear
C)
\[Al\]
done
clear
D)
\[Zn\]
done
clear
View Answer play_arrow
question_answer 106) On moving top to bottom in a group
A)
ionisation potential increases
done
clear
B)
electronegativity increases
done
clear
C)
oxidising strength increases
done
clear
D)
reducing strength increases
done
clear
View Answer play_arrow
question_answer 107) Power alcohol is
A)
absolute alcohol\[+C{{H}_{3}}OH\]
done
clear
B)
absolute alcohol\[+{{C}_{6}}{{H}_{5}}OH\]
done
clear
C)
absolute alcohol + petrol + benzene
done
clear
D)
absolute alcohol\[+C{{H}_{3}}COOH\]
done
clear
View Answer play_arrow
question_answer 108) Which of the following is the most stable ion?
A)
\[C{{H}_{3}}C{{H}_{2}}\overset{+}{\mathop{C}}\,{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}-\overset{+}{\mathop{C}}\,H-C{{H}_{3}}\]
done
clear
C)
\[{{(C{{H}_{3}})}_{3}}{{C}^{+}}\]
done
clear
D)
\[\overset{+}{\mathop{C}}\,{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 109) \[{{N}_{2}}+3{{H}_{2}}2N{{H}_{3}}+22.4\,k\,cal\] What are the favourable condition for the formation of ammonia in the above reaction?
A)
High temperature and low pressure
done
clear
B)
Low temperature and high pressure
done
clear
C)
High temperature and high pressure
done
clear
D)
Low temperature and low pressure
done
clear
View Answer play_arrow
question_answer 110) Homolytic fission produces
A)
free radical
done
clear
B)
carbocation
done
clear
C)
carbonion
done
clear
D)
carbine
done
clear
View Answer play_arrow
question_answer 111) \[C{{H}_{3}}C{{H}_{2}}OH\]and\[C{{H}_{3}}-O-C{{H}_{3}}\]is
A)
position isomers
done
clear
B)
functional isomers
done
clear
C)
chain isomers
done
clear
D)
geometrical isomers
done
clear
View Answer play_arrow
question_answer 112) The IUPAC name of \[C{{H}_{3}}-C{{H}_{2}}-\underset{\begin{smallmatrix} | \\ C{{H}_{2}}-C{{H}_{2}}-C{{H}_{2}}-C{{H}_{3}} \end{smallmatrix}}{\overset{\begin{smallmatrix} C{{H}_{2}}-C{{H}_{3}} \\ | \end{smallmatrix}}{\mathop{C}}}\,-C{{H}_{3}}\]
A)
3-ethyl-4-methyl hexane
done
clear
B)
3-ethyl-3-methyl heptane
done
clear
C)
5-methyl-5-ethyl heptane
done
clear
D)
2-butyl-2-ethyl butane
done
clear
View Answer play_arrow
question_answer 113) Alkaline\[KMn{{O}_{4}}\]is called
A)
Tollen's reagent
done
clear
B)
Baeyefs reagent
done
clear
C)
Benedict solution
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 114) Acidic hydrogen is present in:
A)
\[C{{H}_{3}}-C{{H}_{3}}\]
done
clear
B)
\[C{{H}_{3}}CH=C{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}-CH=CH-C{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}-C=CH\]
done
clear
View Answer play_arrow
question_answer 115) The dipole moment of\[CC{{l}_{4}}\]is zero. It is due to:
A)
planar structure
done
clear
B)
tetrahedral structure
done
clear
C)
same size of C and\[Cl\]atoms
done
clear
D)
same electron affinity of C and\[Cl\]atoms
done
clear
View Answer play_arrow
question_answer 116) What will obtain on adding 50%\[NaOH\]in bauxite?
A)
\[Al\]
done
clear
B)
\[Al{{(OH)}_{3}}\]
done
clear
C)
\[NaAl{{O}_{2}}\]
done
clear
D)
\[Fe\]
done
clear
View Answer play_arrow
question_answer 117) Which is deviated from Aufbau's principle?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
question_answer 118) \[C{{H}_{3}}-C\equiv CH+{{H}_{2}}O\xrightarrow[{}]{{{H}^{+}}/H{{g}^{2+}}}X,\]Compound X, is
A)
\[C{{H}_{3}}C{{H}_{2}}CHO\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}COOH\]
done
clear
C)
\[C{{H}_{3}}COC{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}-CH=C{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 119) \[X+CHC{{l}_{3}}+3KOH\xrightarrow[{}]{{}}Y\] Y is a abnoxious odour compound. The compound X, is
A)
\[C{{H}_{3}}CON{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}N{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}OH\]
done
clear
D)
\[C{{H}_{3}}Cl\]
done
clear
View Answer play_arrow
question_answer 120) The pH of solution which obtains on adding 10 mL 0.2 M\[NaOH\]solution with 10 mL 0.1 M \[{{H}_{2}}S{{O}_{4}}\]will be
A)
zero
done
clear
B)
2.0
done
clear
C)
4.0
done
clear
D)
7.0
done
clear
View Answer play_arrow
question_answer 121) The shape of electron cloud is determined by
A)
principal quantum number
done
clear
B)
azimuthal quantum number
done
clear
C)
spin quantum number
done
clear
D)
All of the above
done
clear
View Answer play_arrow
question_answer 122) The oxidation number of Cr in\[{{K}_{2}}Cr{{O}_{4}}\]is
A)
+3
done
clear
B)
\[-3\]
done
clear
C)
+6
done
clear
D)
\[-6\]
done
clear
View Answer play_arrow
question_answer 123) Which of the following compound contains both ionic and covalent bond?
A)
\[{{H}_{2}}O\]
done
clear
B)
\[S{{O}_{2}}\]
done
clear
C)
\[N{{H}_{4}}Cl\]
done
clear
D)
\[N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 124) On moving left to right in a period, the electropositive character
A)
increases
done
clear
B)
decreases
done
clear
C)
first increases then decreases
done
clear
D)
first decreases then increases
done
clear
View Answer play_arrow
question_answer 125) Bond angle and bond length in benzene are
A)
\[120{}^\circ \]and 1.34\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
B)
\[120{}^\circ \]and 1.39\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
C)
\[180{}^\circ \]and 1.33\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
D)
\[120{}^\circ \] and 1.54\[\overset{o}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 126) The atomic number of a element is 33. It belongs to
A)
third period and IVA group
done
clear
B)
fourth period and IIIA group
done
clear
C)
fourth period and VA group
done
clear
D)
third period and VA group
done
clear
View Answer play_arrow
question_answer 127) Which of the following compound is used as both oxidant and reductant?
A)
\[NaOH\]
done
clear
B)
\[{{K}_{2}}C{{r}_{2}}{{O}_{7}}\]
done
clear
C)
\[{{H}_{2}}{{O}_{2}}\]
done
clear
D)
\[{{H}_{2}}S{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 128) \[{{(C{{H}_{3}}CO)}_{2}}O+HCl\xrightarrow[{}]{{}}X+C{{H}_{3}}COOH\] Compound X, will be
A)
\[C{{H}_{3}}Cl\]
done
clear
B)
\[C{{H}_{3}}COCl\]
done
clear
C)
\[C{{H}_{3}}COC{{H}_{3}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 129) Which of the following is diamagnetic?
A)
\[{{O}_{2}}\]
done
clear
B)
\[NO\]
done
clear
C)
\[{{O}_{2}}\]
done
clear
D)
\[{{F}_{2}}\]
done
clear
View Answer play_arrow
question_answer 130) Lewis acid is
A)
\[C{{l}^{-}}\]
done
clear
B)
\[B{{F}_{3}}\]
done
clear
C)
\[N{{H}_{3}}\]
done
clear
D)
\[NO_{2}^{-}\]
done
clear
View Answer play_arrow
question_answer 131)
A)
Gattermann reaction
done
clear
B)
Schmidt reaction
done
clear
C)
Schotten-Baumann reaction
done
clear
D)
Friedel-Craft's reaction
done
clear
View Answer play_arrow
question_answer 132) Malachite is the ore of which metal?
A)
\[Fe\]
done
clear
B)
\[Cu\]
done
clear
C)
\[Al\]
done
clear
D)
\[Ag\]
done
clear
View Answer play_arrow
question_answer 133) Alkyl halide reacts with alcoholic KOH to give
A)
alcohol
done
clear
B)
alkene
done
clear
C)
alkane
done
clear
D)
aldehyde
done
clear
View Answer play_arrow
question_answer 134) The concentration of pyrite ore is done by which method
A)
calcination
done
clear
B)
roasting
done
clear
C)
froth floatation
done
clear
D)
gravity separation
done
clear
View Answer play_arrow
question_answer 135) Which of the following reaction will not happen?
A)
\[Fe+{{H}_{2}}S{{O}_{4}}\xrightarrow[{}]{{}}FeS{{O}_{4}}+{{H}_{2}}\]
done
clear
B)
\[Cu+2AgN{{O}_{3}}\xrightarrow[{}]{{}}Cu{{(N{{O}_{3}})}_{2}}+2Ag\]
done
clear
C)
\[2KBr+{{I}_{2}}\xrightarrow[{}]{{}}2KI+B{{r}_{2}}\]
done
clear
D)
\[CuO+{{H}_{2}}\xrightarrow[{}]{{}}Cu+{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 136) \[SnC{{l}_{4}}+2FeC{{l}_{2}}\xrightarrow[{}]{{}}SnC{{l}_{2}}+2FeC{{l}_{3}}\] In this reaction, oxidising agent and reducing agent are respectively
A)
\[SnC{{l}_{2}}\]and \[FeC{{l}_{3}}\]
done
clear
B)
\[FeC{{l}_{3}}\]and\[SnC{{l}_{4}}\]
done
clear
C)
\[FeC{{l}_{2}}\] and \[SnC{{l}_{4}}\]
done
clear
D)
\[SnC{{l}_{4}}\]and \[FeC{{l}_{3}}\]
done
clear
View Answer play_arrow
question_answer 137) The molecular weight of ethyl alcohol and dimethyl ether are equal but the boiling point of ethyl alcohol is greater than dimethyl ether. It is due to
A)
ether is insoluble in water
done
clear
B)
methyl group is attached to oxygen in ether
done
clear
C)
the dipole moment of ethanol is greater
done
clear
D)
ethanol has H-bond
done
clear
View Answer play_arrow
question_answer 138) Which of the following gives iodoform test and Fehling test?
A)
\[HCHO\]
done
clear
B)
\[C{{H}_{3}}COC{{H}_{3}}\]
done
clear
C)
\[C{{H}_{3}}CHO\]
done
clear
D)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
View Answer play_arrow
question_answer 139) \[C{{H}_{3}}COO{{C}_{2}}{{H}_{5}}+C{{H}_{3}}COO{{C}_{2}}{{H}_{5}}\xrightarrow[{}]{{}}\] \[C{{H}_{3}}COC{{H}_{2}}COO{{C}_{2}}{{H}_{5}}+{{C}_{2}}{{H}_{5}}OH\] This reaction is called
A)
Esterification
done
clear
B)
Claisen condensation
done
clear
C)
Williamson's synthesis
done
clear
D)
Trans-esterification
done
clear
View Answer play_arrow
question_answer 140) Which is correct for 2p-orbital?
A)
\[n=1,l=2\]
done
clear
B)
\[n=2,l=1\]
done
clear
C)
\[n=1,l=0\]
done
clear
D)
\[n=2,l=0\]
done
clear
View Answer play_arrow
question_answer 141) Mostly alloys are made by which block of elements
A)
s-block
done
clear
B)
p-block
done
clear
C)
d-block
done
clear
D)
\[f-\]block
done
clear
View Answer play_arrow
question_answer 142) \[C{{H}_{3}}MgI+C{{O}_{2}}\xrightarrow[{}]{{}}X\xrightarrow[{}]{{{H}_{2}}O}Y\] Compound Y, is
A)
\[C{{H}_{3}}OH\]
done
clear
B)
\[C{{H}_{3}}COOH\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
D)
\[C{{H}_{3}}CHO\]
done
clear
View Answer play_arrow
question_answer 143) Which of the following compound obtains on the reaction of formaldehyde with\[C{{H}_{3}}MgX\]?
A)
\[C{{H}_{3}}CHO\]
done
clear
B)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
C)
\[HCOOH\]
done
clear
D)
\[C{{H}_{3}}COOH\]
done
clear
View Answer play_arrow
question_answer 144) Which of the following is not soluble in cone. \[{{H}_{2}}S{{O}_{4}}\]?
A)
\[n-\]hexane
done
clear
B)
hexene
done
clear
C)
benzene
done
clear
D)
ethanol
done
clear
View Answer play_arrow
question_answer 145) Conjugated base of\[C{{H}_{2}}C{{l}_{2}}\]is
A)
\[C{{O}_{2}}\]
done
clear
B)
\[{{H}_{2}}C{{O}_{3}}\]
done
clear
C)
\[{{H}_{2}}O\]
done
clear
D)
\[CO_{3}^{2-}\]
done
clear
View Answer play_arrow
question_answer 146) Ethylene can obtained by the electrolysis of
A)
potassium fumarate
done
clear
B)
potassium succinate
done
clear
C)
potassium maleate
done
clear
D)
potassium formate
done
clear
View Answer play_arrow
question_answer 147) The electronic configuration of-alkaline earth metal is
A)
\[n{{s}^{1}}\]
done
clear
B)
\[n{{s}^{2}}\]
done
clear
C)
\[n{{p}^{6}}\]
done
clear
D)
\[n{{s}^{2}}(n-1){{d}^{10}}\]
done
clear
View Answer play_arrow
question_answer 148) The oxidation number of C-atom in\[C{{H}_{2}}C{{l}_{2}}\]and\[CC{{l}_{4}}\]is respectively
A)
zero and 4
done
clear
B)
zero and -4
done
clear
C)
2 and 4
done
clear
D)
-2 and -4
done
clear
View Answer play_arrow
question_answer 149) \[C{{H}_{3}}-O-{{C}_{3}}{{H}_{7}}\]and\[{{C}_{2}}{{H}_{5}}-O-{{C}_{2}}{{H}_{5}}\]show the following isomerism
A)
position
done
clear
B)
functional
done
clear
C)
metamerism
done
clear
D)
tautomerism
done
clear
View Answer play_arrow
question_answer 150) \[C{{H}_{3}}CHO+C{{H}_{3}}MgBr\xrightarrow[{}]{{}}A\] Compound A, is
A)
a perimary alcohol
done
clear
B)
a secondary alcohol
done
clear
C)
a tertiary alcohol
done
clear
D)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} || \\ O \end{smallmatrix}}{\mathop{C}}\,-C{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 151) The electronic configuration of dication of a element is 2, 8, 14. The atomic number of this element will be
A)
26
done
clear
B)
24
done
clear
C)
25
done
clear
D)
28
done
clear
View Answer play_arrow
question_answer 152) \[RCOOH\xrightarrow[{}]{Soda\lim e}X+C{{O}_{2}}\] Compound X, is
A)
\[RH\]
done
clear
B)
\[RC{{H}_{3}}\]
done
clear
C)
\[R-R\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 153) \[RMgI+C{{H}_{3}}OH\xrightarrow[{}]{{}}X\] Compound X, is
A)
RH
done
clear
B)
\[RC{{H}_{3}}\]
done
clear
C)
\[ROH\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 154) On moving left to right in period, the ionization potential
A)
increases
done
clear
B)
decreases
done
clear
C)
first increases then decreases
done
clear
D)
first decreases then increases
done
clear
View Answer play_arrow
question_answer 155) Lithium and magnesium show the similarity in characteristics because
A)
both find in nature along
done
clear
B)
both have approximately same size
done
clear
C)
both have same electronic configuration
done
clear
D)
their ratio of charge and size are approximately same
done
clear
View Answer play_arrow
question_answer 156) Which of the following character always increases on moving top to bottom in group?
A)
ionization potential
done
clear
B)
electron affinity
done
clear
C)
electronegativity
done
clear
D)
atomic radius
done
clear
View Answer play_arrow
question_answer 157) In the extraction of copper, its ore is heated at high temperature, in the presence of air. This process is called
A)
smelting
done
clear
B)
calcination
done
clear
C)
roasting
done
clear
D)
distillation
done
clear
View Answer play_arrow
question_answer 158) A white precipitate of silver chloride is obtained on adding silver nitrate in sodium chloride solution because
A)
\[NaCl\]is insoluble in water
done
clear
B)
CF ion is present in\[NaCl\]
done
clear
C)
\[AgN{{O}_{3}}\]is insoluble in\[NaCl\]solution
done
clear
D)
\[NaCl\]is a inorganic compound
done
clear
View Answer play_arrow
question_answer 159) Aromatic compounds give mainly following reaction
A)
electrophilic addition
done
clear
B)
nucleophilic addition
done
clear
C)
nucleophilic substitution
done
clear
D)
electrophilic substitution
done
clear
View Answer play_arrow
question_answer 160) The\[[{{H}^{+}}]\]of a solution is 1 mol/L. Its pH will be
A)
1.0
done
clear
B)
10.0
done
clear
C)
0.1
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 161) On ozonolysis of a alkene, only single organic compound obtains. Alkene is
A)
\[C{{H}_{3}}-CH=C{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}CH=CH-C{{H}_{3}}\]
done
clear
C)
\[C{{H}_{3}}-\underset{\begin{smallmatrix} | \\ C{{H}_{3}} \end{smallmatrix}}{\mathop{C}}\,=C{{H}_{2}}\]
done
clear
D)
\[C{{H}_{3}}-C{{H}_{2}}-CH=C{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 162) On adding\[N{{H}_{4}}OH\]in equilibrium \[N{{H}_{4}}ClNH_{4}^{+}+C{{l}^{-}}\]
A)
more\[C{{l}^{-}}\]will form
done
clear
B)
more\[N{{H}_{4}}Cl\]will decompose
done
clear
C)
more\[NH_{4}^{+}\]will form
done
clear
D)
decomposition of\[N{{H}_{4}}Cl\]will reduce
done
clear
View Answer play_arrow
question_answer 163) For an electron\[n=2,\text{ }l=1\]. Total magnetic quantum number for this will be
A)
3
done
clear
B)
2
done
clear
C)
1
done
clear
D)
zero
done
clear
View Answer play_arrow
question_answer 164) The aqueous solution of a salt is basic. It is the salt of
A)
strong acid and strong base
done
clear
B)
strong acid and weak base
done
clear
C)
weak acid and weak base
done
clear
D)
weak acid and strong base
done
clear
View Answer play_arrow
question_answer 165) During the extraction of aluminium, cryolite adds in alumina
A)
to obtain pure\[Al\]
done
clear
B)
to dissolve alumina
done
clear
C)
to remove impurities
done
clear
D)
to catalysis
done
clear
View Answer play_arrow
question_answer 166) The main product of the reaction of \[C{{H}_{3}}C{{H}_{2}}N{{H}_{2}}\]with nitrous acid
A)
\[C{{H}_{3}}CN\]
done
clear
B)
\[C{{H}_{3}}ONO\]
done
clear
C)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
D)
\[C{{H}_{3}}-N=O\]
done
clear
View Answer play_arrow
question_answer 167) \[A+NaN{{O}_{2}}+HCl\xrightarrow[{}]{{}}C{{O}_{2}}+{{N}_{2}}+{{H}_{2}}O\] Compound A, is
A)
\[N{{H}_{2}}CON{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}N{{H}_{2}}\]
done
clear
C)
\[C{{H}_{3}}NC\]
done
clear
D)
\[C{{H}_{3}}CON{{H}_{2}}\]
done
clear
View Answer play_arrow
question_answer 168) If a system in equilibrium is subjected to a change of concentration, temperature or pressure the equilibrium shifts in a direction so as to undo the effect of the change imposed. This law is known as
A)
Le-Chatelier's principle
done
clear
B)
Avogadro's principle
done
clear
C)
Guldberg-Waage principle
done
clear
D)
Gay-Lussac's principle
done
clear
View Answer play_arrow
question_answer 169) Alkaline hydrolysis of ethyl acetate gives
A)
\[C{{H}_{3}}COOH\] and\[{{C}_{2}}{{H}_{5}}OH\]
done
clear
B)
\[C{{H}_{3}}COONa\]and \[{{C}_{2}}{{H}_{5}}OH\]
done
clear
C)
\[C{{H}_{3}}COOH\]and \[N{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}COONa\]and \[N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 170) Which of the following will reduce the Tollen's reagent?
A)
\[HCOOH\]
done
clear
B)
\[C{{H}_{3}}COOH\]
done
clear
C)
\[HOOC-COOH\]
done
clear
D)
\[{{C}_{6}}{{H}_{5}}COOH\]
done
clear
View Answer play_arrow
question_answer 171) For the reaction, \[2S{{O}_{3}}2S{{O}_{2}}+{{O}_{2}}\] the expression for the equilibrium constant \[({{K}_{c}})\]is
A)
\[\frac{2[S{{O}_{2}}][{{O}_{2}}]}{2[S{{O}_{3}}]}\]
done
clear
B)
\[\frac{[S{{O}_{2}}][{{O}_{2}}]}{[S{{O}_{3}}]}\]
done
clear
C)
\[\frac{{{[S{{O}_{3}}]}^{2}}}{[S{{O}_{2}}][{{O}_{2}}]}\]
done
clear
D)
\[\frac{{{[S{{O}_{2}}]}^{2}}[{{O}_{2}}]}{{{[S{{O}_{3}}]}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 172) The electronic configuration of Fe is
A)
2, 8, 14, 2
done
clear
B)
2, 8, 8. 6, 2
done
clear
C)
2, 6, 18
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 173)
The following reaction is called \[{{C}_{6}}{{H}_{5}}OH+3KOH+CHC{{l}_{3}}\to \]
A)
Kolbe-Schmidt reaction
done
clear
B)
Gattermann reaction
done
clear
C)
Fries rearrangement
done
clear
D)
Reimer-Tiemann reaction
done
clear
View Answer play_arrow
question_answer 174) The product of the reaction of chloroform with cone.\[HN{{O}_{3}}\]is
A)
chloretone
done
clear
B)
chloropicrin
done
clear
C)
nitromethane
done
clear
D)
methyl nitrite
done
clear
View Answer play_arrow
question_answer 175) At equilibrium in a reversible reaction the catalyst
A)
increases the rate of forward direction
done
clear
B)
increases the rate of backward direction
done
clear
C)
increases the rate of forward and backward direction equally
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 176) The process of conversion of higher hydrocarbon to lower hydrocarbon is called
A)
isomerisation
done
clear
B)
cracking
done
clear
C)
hydroformation
done
clear
D)
mining
done
clear
View Answer play_arrow
question_answer 177) Which of the following reagent will differentiate in propene and propyne?
A)
Alkaline \[KMn{{O}_{4}}\]
done
clear
B)
Bromine water
done
clear
C)
\[{{[Ag{{(N{{H}_{3}})}_{2}}]}^{+}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 178) Which of the following is Hofmann bromamide reaction?
A)
\[RCN+4H\xrightarrow[{}]{{}}RC{{H}_{2}}N{{H}_{2}}\]
done
clear
B)
\[C{{H}_{3}}COCl+C{{H}_{3}}OH\xrightarrow[{}]{{}}\] \[C{{H}_{3}}COOC{{H}_{3}}+HCl\]
done
clear
C)
\[C{{H}_{3}}CN+{{H}_{2}}O\xrightarrow[{}]{NaOH}C{{H}_{3}}COONa+N{{H}_{3}}\]
done
clear
D)
\[C{{H}_{3}}COON{{H}_{2}}+B{{r}_{2}}+4KOH\xrightarrow[{}]{{}}\] \[C{{H}_{3}}N{{H}_{2}}+{{K}_{2}}C{{O}_{3}}+2KBr+2{{H}_{2}}O\]
done
clear
View Answer play_arrow
question_answer 179) The solubility product of PbS is\[3.4\times {{10}^{-28}}\]. If the concentration of\[P{{b}^{2+}}\]is\[1\times {{10}^{-2}}\]mol then the concentration of\[{{S}^{2-}}\]at which\[PbS\]will precipitated
A)
\[3.4\times {{10}^{-26}}\]
done
clear
B)
\[3.4\times {{10}^{-30}}\]
done
clear
C)
\[1\times {{10}^{-2}}\]
done
clear
D)
\[3.4\times {{10}^{-22}}\]
done
clear
View Answer play_arrow
question_answer 180) Formaldehyde reacts with ammonia to give following compound
A)
formalin
done
clear
B)
formaldehyde ammonia
done
clear
C)
hexamethylene tetraamine
done
clear
D)
formamide
done
clear
View Answer play_arrow
question_answer 181) Which of the following characteristics does not show byd-block elements?
A)
Variable valency
done
clear
B)
Formation to complex compound
done
clear
C)
Diamagnetism
done
clear
D)
Paramagnetism
done
clear
View Answer play_arrow
question_answer 182) \[RX+2Na+RX\xrightarrow[{}]{{}}R-R+2NaX\] The above reaction is called
A)
Wurtz reaction
done
clear
B)
Williamson's synthesis
done
clear
C)
Kolbe's electrolysis
done
clear
D)
Sabatier-Sendern's reaction
done
clear
View Answer play_arrow
question_answer 183) \[C{{H}_{3}}COOAg+B{{r}_{2}}\xrightarrow[{}]{\Delta }C{{H}_{3}}Br+AgBr+C{{O}_{2}}\] This reaction is called
A)
Hofmann mustard oil reaction
done
clear
B)
Hell Volhard Zeiinsky reaction
done
clear
C)
Hunsdiecker reaction
done
clear
D)
Wurtz-Fittig reaction
done
clear
View Answer play_arrow
question_answer 184) For precipitation
A)
Solubility product = ionic product
done
clear
B)
Solubility product > ionic product
done
clear
C)
Solubility product < ionic product
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 185) HCHO + 40% strong alkaline solution\[\xrightarrow[{}]{{}}\] Products one of the product in this reaction is
A)
\[C{{H}_{3}}C{{H}_{2}}OH\]
done
clear
B)
\[C{{H}_{3}}COOH\]
done
clear
C)
\[CH\equiv CH\]
done
clear
D)
\[C{{H}_{3}}OH\]
done
clear
View Answer play_arrow
question_answer 186) Which of the following reaction will not affected by pressure?
A)
\[{{N}_{2}}+3{{H}_{2}}2N{{H}_{3}}\]
done
clear
B)
\[{{N}_{2}}+{{O}_{2}}2NO\]
done
clear
C)
\[2S{{O}_{2}}+{{O}_{2}}2S{{O}_{3}}\]
done
clear
D)
\[PC{{l}_{3}}+C{{l}_{2}}PC{{l}_{5}}\]
done
clear
View Answer play_arrow
question_answer 187) In an atom, two electrons do not have identical set of four quantum number. This statement is belong to
A)
Hund's law
done
clear
B)
Aufbau's law
done
clear
C)
\[(n+l)\] law
done
clear
D)
Fault's law
done
clear
View Answer play_arrow
question_answer 188) In froth floatation method of ore concen-tration, ore particles rise to the surface because
A)
they are light
done
clear
B)
these are insoluble
done
clear
C)
their surface do not wet with water easily
done
clear
D)
these contain electric charge
done
clear
View Answer play_arrow
question_answer 189) Which of the following is amphoteric oxide?
A)
\[MgO\]
done
clear
B)
\[A{{l}_{2}}{{O}_{3}}\]
done
clear
C)
\[{{K}_{2}}O\]
done
clear
D)
\[CuO\]
done
clear
View Answer play_arrow
question_answer 190) Alkaline hydrolysis of a ester is called
A)
hydrolysis
done
clear
B)
saponification
done
clear
C)
neutralization
done
clear
D)
hydrogenation
done
clear
View Answer play_arrow
question_answer 191) The number of n electrons present in a aromatic ring are
A)
\[(4+2)n\]
done
clear
B)
\[(4+2n)\]
done
clear
C)
\[(4n+2)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 192) Picric acid is
A)
ortho-nitrophenol
done
clear
B)
2, 4, 6-trinitro benzoic acid
done
clear
C)
2, 4, 6-trinitrophenol
done
clear
D)
2, 4-dinitrophenol
done
clear
View Answer play_arrow
question_answer 193) The correct radius order of atom, its cation and anion is
A)
atom < cation > anion
done
clear
B)
atom > cation < anion
done
clear
C)
atom = cation = anion
done
clear
D)
atom > cation > anion
done
clear
View Answer play_arrow
question_answer 194) \[C{{H}_{3}}C{{H}_{2}}I+NaOR\xrightarrow[{}]{{}}C{{H}_{3}}C{{H}_{2}}OR+NaI\] This reaction is
A)
Wurtz reaction
done
clear
B)
Williamson's synthesis
done
clear
C)
Wittig reaction
done
clear
D)
Curtius reaction
done
clear
View Answer play_arrow
question_answer 195) Saturated hydrocarbon gives
A)
free radical substitution
done
clear
B)
free radical addition
done
clear
C)
electrophilic substitution
done
clear
D)
electrophilic addition
done
clear
View Answer play_arrow
question_answer 196) \[{{N}_{2}}+{{O}_{2}}2NO;\] \[\Delta H=43.2\,kcal\] Equilibrium will go in forward direction
A)
on increasing temperature
done
clear
B)
on decreasing temperature
done
clear
C)
on increasing pressure
done
clear
D)
on decreasing pressure
done
clear
View Answer play_arrow
question_answer 197) Ethanal forms 3-hydroxy butanal on reaction with alkali. This reaction is
A)
Claisen condensation
done
clear
B)
Polymerization
done
clear
C)
Aldol condensation
done
clear
D)
Reimer-Tiemann reaction
done
clear
View Answer play_arrow
question_answer 198) Absolute alcohol can obtained from absolute spirit by which process
A)
steam distillation
done
clear
B)
fractional distillation
done
clear
C)
azerotropic distillation
done
clear
D)
hydrolysis
done
clear
View Answer play_arrow
question_answer 199) Ethyl alcohol is obtained from sugar by following enzyme reaction
A)
invertase
done
clear
B)
zymase
done
clear
C)
maltase
done
clear
D)
diastase
done
clear
View Answer play_arrow
question_answer 200) Brass is a
A)
alloy
done
clear
B)
transition metal
done
clear
C)
non-metal
done
clear
D)
element
done
clear
View Answer play_arrow
question_answer 201) If\[\frac{x-a}{b+c}+\frac{x-b}{c+a}+\frac{x-c}{a+b}=3,\]then the value of\[x\] is
A)
\[a+b+c\]
done
clear
B)
\[abc\]
done
clear
C)
1
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 202) If one root of the equation\[{{x}^{2}}+px+12=0\]is 4 when equation\[{{x}^{2}}+px+q=0\]have equal roots, then the value of\[q\]is
A)
\[\frac{4}{49}\]
done
clear
B)
\[\frac{49}{4}\]
done
clear
C)
\[4\]
done
clear
D)
\[\frac{1}{4}\]
done
clear
View Answer play_arrow
question_answer 203) The real roots of the equation\[{{x}^{2}}+5|x|+4=0\]are
A)
\[(-1,-4)\]
done
clear
B)
\[(\pm 1,\pm 4)\]
done
clear
C)
\[(-4,4)\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 204) In a GP,\[(p+q)\]th term is 211 and\[(p-q)\]th term is n, then the value of pth term is
A)
\[\frac{m}{n}\]
done
clear
B)
\[\sqrt{\frac{m}{n}}\]
done
clear
C)
\[\sqrt{mn}\]
done
clear
D)
\[\sqrt{\left( \frac{n}{m} \right)}\]
done
clear
View Answer play_arrow
question_answer 205) If a, b, c are in AP, then\[\frac{a}{bc},\frac{1}{c},\frac{1}{b}\]will be in
A)
AP
done
clear
B)
GP
done
clear
C)
HP
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 206) If\[{{a}^{1/x}}={{b}^{1/y}}={{c}^{1/z}}\]and\[a,b,c\]are in GP, then\[x,y,z\]will be in
A)
AP
done
clear
B)
GP
done
clear
C)
HP
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 207) In the expansion of\[{{\left( \frac{x}{3}-\frac{2}{{{x}^{2}}} \right)}^{10}},\]the rth term contains\[{{x}^{4}},\]then the value of r is
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
5
done
clear
View Answer play_arrow
question_answer 208) Sum of the series\[\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{3.4}-\frac{1}{4.5}+....\]is
A)
\[log\text{ }2\]
done
clear
B)
\[log\text{ }3\]
done
clear
C)
\[2\text{ }log\text{ }2-1\]
done
clear
D)
\[2\text{ }log\text{ }3-1\]
done
clear
View Answer play_arrow
question_answer 209) If\[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}=1,\]then\[ab+bc+ca\]lies in the interval
A)
\[\left[ \frac{1}{2},2 \right]\]
done
clear
B)
\[[-1,2]\]
done
clear
C)
\[\left[ -\frac{1}{2},1 \right]\]
done
clear
D)
\[\left[ -1,\frac{1}{2} \right]\]
done
clear
View Answer play_arrow
question_answer 210) In the 13 cricket players, 4 are bowlers and 2 are wicket keepers, then in how many ways can form a cricket team of 11 players in which one wicket keeper and atleast 3 bowlers included, is
A)
112
done
clear
B)
22
done
clear
C)
8
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 211) Two dice are tossed together. The probability that the sum of the numbers appeared on both dice is 5, is
A)
\[\frac{1}{8}\]
done
clear
B)
\[\frac{1}{9}\]
done
clear
C)
\[\frac{1}{12}\]
done
clear
D)
\[\frac{1}{16}\]
done
clear
View Answer play_arrow
question_answer 212) Between two players a coin is tossed 4 times. The probability that both players get equal number of heads, is
A)
\[\frac{1}{16}\]
done
clear
B)
\[\frac{5}{256}\]
done
clear
C)
\[\frac{35}{128}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 213) A pack of cards contains 4 aces, 4 kings, 4 queens and 4 jacks. Two cards are drawn at random from this pack without replacement. The probability that atleast one of them will be an aces, is
A)
\[\frac{1}{5}\]
done
clear
B)
\[\frac{3}{16}\]
done
clear
C)
\[\frac{9}{20}\]
done
clear
D)
\[\frac{1}{9}\]
done
clear
View Answer play_arrow
question_answer 214) If\[A=\left[ \begin{matrix} 1 & 2 \\ 2 & 3 \\ \end{matrix} \right],\]then the value of\[{{A}^{-1}}\]is
A)
\[\left[ \begin{matrix} -3 & 2 \\ 2 & -1 \\ \end{matrix} \right]\]
done
clear
B)
\[\left[ \begin{matrix} 3 & 2 \\ 2 & 1 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} 1 & 2 \\ 2 & 3 \\ \end{matrix} \right]\]
done
clear
D)
\[\left[ \begin{matrix} 3 & -2 \\ -2 & 1 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 215) The value of\[\left| \begin{matrix} b+c & a+b & a \\ c+a & b+c & b \\ a+b & c+a & c \\ \end{matrix} \right|\]is
A)
\[{{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc\]
done
clear
B)
\[0\]
done
clear
C)
\[2abc(a+b+c)\]
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 216) If\[f:R\to R\]and\[f(x)=tan\text{ }x,\]then value of\[{{f}^{-1}}(1)\]is
A)
\[\left\{ n\pi +\frac{\pi }{4},n\in Z \right\}\]
done
clear
B)
\[\frac{\pi }{4}\]
done
clear
C)
does not exist
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 217) The value of\[\underset{x\to 0}{\mathop{\lim }}\,\frac{1-\cos x}{{{x}^{2}}}\]is
A)
0
done
clear
B)
\[\frac{1}{4}\]
done
clear
C)
\[\frac{1}{2}\]
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 218) If function \[f(x)=\left\{ \begin{matrix} {{x}^{2}}/a & ,0\le x<1 \\ a & ,1\le x<\sqrt{2} \\ \frac{(2{{b}^{2}}-4b)}{{{x}^{2}}} & \sqrt{2}\le x<\infty \\ \end{matrix} \right.\] is continuous for\[0<x<\infty ,\]then the values of\[a\] and\[b\]are
A)
\[a=1,b=-1\]
done
clear
B)
\[a=-1,b=1\]
done
clear
C)
\[a=-1,b\text{ }=1+\sqrt{2}\]
done
clear
D)
\[a=-1,b=\sqrt{2}-1\]
done
clear
View Answer play_arrow
question_answer 219) The value of\[\underset{x\to \infty }{\mathop{\lim }}\,=\frac{{{x}^{2}}\sin \left( \frac{1}{x} \right)-x}{1-|x|}\]is
A)
\[-1\]
done
clear
B)
\[1\]
done
clear
C)
0
done
clear
D)
\[\infty \]
done
clear
View Answer play_arrow
question_answer 220) If\[{{x}^{y}}.{{y}^{x}}=1,\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{y(x+y\log x)}{x(y+x\log y)}\]
done
clear
B)
\[\frac{y(y+x\log y)}{x(y\log x+y)}\]
done
clear
C)
\[-\frac{y(y+x\log y)}{x(y\log x+x)}\]
done
clear
D)
\[-\frac{y(x+y\log x)}{x(y+x\log y)}\]
done
clear
View Answer play_arrow
question_answer 221) If\[{{y}^{2}}=a{{e}^{-2x}}+\frac{2}{5}(\cos x-2\sin x),\]then the value of\[y\frac{dy}{dx}+{{y}^{2}}+\sin x\] is
A)
0
done
clear
B)
\[-1\]
done
clear
C)
1
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 222) If\[p(x)\]is a cubic polynomial and\[p(0)=4,\] \[p'(0)=3,p''(0)=4,p'''(0)=6,\]then the value of\[p'(-1)\]is
A)
2
done
clear
B)
\[-10\]
done
clear
C)
10
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 223) The angle of intersection of the curves\[y={{x}^{2}}\] and\[6y=7-{{x}^{3}}\]at point (1,1), is
A)
\[\frac{\pi }{4}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{2}\]
done
clear
D)
\[\pi \]
done
clear
View Answer play_arrow
question_answer 224) Curves\[a{{x}^{2}}+b{{y}^{2}}=1\]and\[a'{{x}^{2}}+b'{{y}^{2}}=1\]intersect each other orthogonally, if
A)
\[\frac{1}{a}+\frac{1}{a'}=\frac{1}{b}+\frac{1}{b'}\]
done
clear
B)
\[\frac{1}{a}+\frac{1}{b}=\frac{1}{a'}+\frac{1}{b'}\]
done
clear
C)
\[\frac{1}{a}-\frac{1}{b}=\frac{1}{a'}-\frac{1}{b'}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 225) In the interval\[[-1,2],\]function\[f(x)=|x|+|x-1|\]will be
A)
constant
done
clear
B)
increasing
done
clear
C)
decreasing
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 226) The equation of tangent to the parabola \[{{y}^{2}}=4x\]at point (1, 2) is
A)
\[x-y+1=0\]
done
clear
B)
\[x+y+1=0\]
done
clear
C)
\[x+y-1=0\]
done
clear
D)
\[x-y-1=0\]
done
clear
View Answer play_arrow
question_answer 227) The distance covered by a particle in t second is\[s=a{{e}^{t}}+b{{e}^{-t}}\]. At time t the acceleration of the particle is
A)
\[s\,m/{{s}^{2}}\]
done
clear
B)
\[as\,m/{{s}^{2}}\]
done
clear
C)
\[bs\text{ }m/{{s}^{2}}\]
done
clear
D)
\[-bs\text{ }m/{{s}^{2}}\]
done
clear
View Answer play_arrow
question_answer 228) The value of\[\int{{{x}^{2}}{{e}^{{{x}^{3}}}}}\cos ({{e}^{{{x}^{3}}}})dx\] is
A)
\[\sin ({{e}^{{{x}^{3}}}})+c\]
done
clear
B)
\[\frac{1}{3}\sin ({{e}^{{{x}^{3}}}})+c\]
done
clear
C)
\[-\frac{1}{3}\sin ({{e}^{{{x}^{3}}}})+c\]
done
clear
D)
\[3\sin ({{e}^{{{x}^{3}}}})+c\]
done
clear
View Answer play_arrow
question_answer 229) If \[\int_{0}^{\infty }{\frac{{{x}^{2}}dx}{({{x}^{2}}+{{a}^{2}})({{x}^{2}}+{{b}^{2}})({{x}^{2}}+{{c}^{2}})}}\] \[=\frac{\pi }{2(a+b)(b+c)(c+a)},\]then the value of \[\int_{0}^{\infty }{\frac{dx}{({{x}^{2}}+4)({{x}^{2}}+9)}}\]is
A)
\[\frac{\pi }{20}\]
done
clear
B)
\[\frac{\pi }{40}\]
done
clear
C)
\[\frac{\pi }{60}\]
done
clear
D)
\[\frac{\pi }{80}\]
done
clear
View Answer play_arrow
question_answer 230) If\[\int{\frac{dx}{x\sqrt{1-{{x}^{3}}}}=a\log \left| \frac{\sqrt{(1-{{x}^{3}})}-1}{\sqrt{(1-{{x}^{3}})}+1} \right|}+b,\]then the value of a is
A)
\[-\frac{1}{3}\]
done
clear
B)
\[\frac{1}{3}\]
done
clear
C)
\[-\frac{2}{3}\]
done
clear
D)
\[\frac{2}{3}\]
done
clear
View Answer play_arrow
question_answer 231) If\[f(a-x)=f(x),\]then the value of\[\int_{0}^{a}{xf(x)}dx\]is
A)
\[a\int_{0}^{a}{f(x)}dx\]
done
clear
B)
\[\frac{a}{2}\int_{0}^{a}{x\,f(x)\,}dx\]
done
clear
C)
\[\frac{{{a}^{2}}}{2}\int_{0}^{a}{f(x)\,}dx\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 232) The value of\[\int_{0}^{\pi /4}{\frac{\sec x\cos ecx}{\log (\tan x)}}dx\] is
A)
0
done
clear
B)
1
done
clear
C)
does not exist
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 233) The area of the region bounded by the parabola\[{{y}^{2}}=4\text{ a}x\]and its latusrectum is
A)
\[\frac{4a}{3}sq\,unit\]
done
clear
B)
\[\frac{4{{a}^{3}}}{3}sq\,unit\]
done
clear
C)
\[\frac{8a}{3}sq\,unit\]
done
clear
D)
\[\frac{8{{a}^{2}}}{3}sq\,unit\]
done
clear
View Answer play_arrow
question_answer 234) If in the interval\[\left[ 0,\frac{\pi }{2} \right]\]the area of the region bounded by the curve\[y=sin\text{ }x\]and\[x-\]axis is A sq unit, then in the same interval, the area of the region bounded by the curve\[y=cos\text{ }x\] and\[x-\]axis is
A)
A sq unit
done
clear
B)
\[\frac{\pi }{2}-A\] sq unit
done
clear
C)
\[-A\] sq unit
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 235) The equation of the curve which satisfies the differential equation\[(1+{{y}^{2}})dx-xy\,dy=0\] and passes through the point (1, 0) is
A)
\[{{x}^{2}}+{{y}^{2}}=1\]
done
clear
B)
\[{{x}^{2}}-{{y}^{2}}=1\]
done
clear
C)
\[2{{x}^{2}}+{{y}^{2}}=2\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 236) The solution of the differential equation \[\frac{dy}{dx}=\frac{x+y+7}{2x+2y+3}\]is
A)
\[6(x+y)-11\text{ }log\text{ (}3x+3y+10)=9x+c\]
done
clear
B)
\[6(x+y)+11\text{ }log\text{ (}3x+3y+10)=9x+c\]
done
clear
C)
\[6(x+y)-\log \left( x+y+\frac{10}{3} \right)=9x+c\]
done
clear
D)
\[6(x+y)\left( x+y+\frac{10}{3} \right)=9x+c\]
done
clear
View Answer play_arrow
question_answer 237) If \[{{\left( \frac{1-i}{1+i} \right)}^{100}}=a+ib,\]then
A)
\[a=1,b=0\]
done
clear
B)
\[a=0,b=1\]
done
clear
C)
\[a=-1,b=2\]
done
clear
D)
\[a=2,b=-1\]
done
clear
View Answer play_arrow
question_answer 238) If complex numbers\[{{z}_{1}},{{z}_{2}}\]and\[{{z}_{3}}\]represents the vertices of an equilateral triangle such that\[|{{z}_{1}}|=|{{z}_{2}}|=|{{z}_{3}}|,\]then
A)
\[{{z}_{1}}+{{z}_{2}}+{{z}_{3}}\le 0\]
done
clear
B)
\[{{z}_{1}}+{{z}_{2}}+{{z}_{3}}\ge 0\]
done
clear
C)
\[{{z}_{1}}+{{z}_{2}}+{{z}_{3}}=0\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 239) If\[m\sin \theta =n\sin (\theta +2\alpha ),\]then the value of\[\tan (\theta +\alpha )\cot \alpha \]is
A)
\[\frac{m+n}{m-n}\]
done
clear
B)
\[\frac{m-n}{m+n}\]
done
clear
C)
\[\frac{1-n}{1+n}\]
done
clear
D)
\[\frac{1+n}{1-n}\]
done
clear
View Answer play_arrow
question_answer 240) If\[A+B+C=\pi ,\]then\[tan\text{ }A+tan\text{ }B+tan\text{ }C\]is equal to
A)
\[-1\]
done
clear
B)
1
done
clear
C)
\[tan\text{ }A\text{ }tan\text{ }B\text{ }tan\text{ }C\]
done
clear
D)
\[cot\text{ }A\text{ }cot\text{ }B\text{ }cot\text{ }C\]
done
clear
View Answer play_arrow
question_answer 241) The maximum value of\[a\text{ }cos\theta +b\text{ }sin\theta \]is
A)
\[a+b\]
done
clear
B)
\[|a|+|b|\]
done
clear
C)
\[a-b\]
done
clear
D)
\[\sqrt{{{a}^{2}}+{{b}^{2}}}\]
done
clear
View Answer play_arrow
question_answer 242) The general solution of the equation \[(\sqrt{3}-1)\sin \theta +(\sqrt{3}+1)\cos \theta =2\]is
A)
\[2n\pi \pm \frac{\pi }{4}+\frac{\pi }{12}\]
done
clear
B)
\[n\pi +{{(-1)}^{n}}\frac{\pi }{4}+\frac{\pi }{12}\]
done
clear
C)
\[2n\pi \pm \frac{\pi }{4}-\frac{\pi }{12}\]
done
clear
D)
\[n\pi +{{(-1)}^{n}}\frac{\pi }{4}-\frac{\pi }{12}\]
done
clear
View Answer play_arrow
question_answer 243) The value of\[{{\cot }^{-1}}\left[ \frac{\sqrt{(1+\sin x)}+\sqrt{(1-\sin x)}}{\sqrt{(1-\sin x)}-\sqrt{(1+\sin x)}} \right]\] is
A)
\[\frac{x}{2}\]
done
clear
B)
\[\pi -\frac{x}{2}\]
done
clear
C)
\[\pi -x\]
done
clear
D)
\[2\pi -x\]
done
clear
View Answer play_arrow
question_answer 244) In\[\Delta ABC,\]the value of\[a(b\cos C-c\cos B)\]is
A)
0
done
clear
B)
\[{{a}^{2}}\]
done
clear
C)
\[{{b}^{2}}-{{c}^{2}}\]
done
clear
D)
\[{{a}^{2}}-{{b}^{2}}\]
done
clear
View Answer play_arrow
question_answer 245) In\[\Delta \]ABC, if\[\angle A=30{}^\circ ,c=7\sqrt{3}\]and\[\angle C=90{}^\circ ,\] then the value of a is
A)
\[\frac{7}{2}\]
done
clear
B)
\[7\sqrt{3}\]
done
clear
C)
\[\frac{7}{2}\sqrt{3}\]
done
clear
D)
\[7\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 246) The equation of straight line which cut equal intercepts on axes and passes through the point\[(1,-2)\]is
A)
\[x+y=1\]
done
clear
B)
\[x-y=1\]
done
clear
C)
\[x-y=2\]
done
clear
D)
\[x+y+1=0\]
done
clear
View Answer play_arrow
question_answer 247) If the equation of tangent to a circle at point (3, 5) is\[2x-y-1=0\]and its centre lies on \[x+y=5,\]then the equation of circle is
A)
\[{{x}^{2}}+{{y}^{2}}+6x-16y+28=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-6x-16y+28=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+6x+6y+28=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-6x-6y-28=0\]
done
clear
View Answer play_arrow
question_answer 248) The curve represented by the parametric equations \[x=3(\cos t+\sin t),y=4\]\[(cos\text{ }t-sin\text{ }t)\]is
A)
a parabola
done
clear
B)
an ellipse
done
clear
C)
a hyperbola
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 249) Eccentricity of the hyperbola\[{{x}^{2}}-{{y}^{2}}=4\]is
A)
\[\sqrt{2}\]
done
clear
B)
\[2\sqrt{3}\]
done
clear
C)
\[\sqrt{3}\]
done
clear
D)
\[3\sqrt{3}\]
done
clear
View Answer play_arrow
question_answer 250) The equation of the normal to the parabola \[{{y}^{2}}=4x\]which is parallel to the line \[y=2x-5,\]is
A)
\[y=2x\]
done
clear
B)
\[y=2x-10\]
done
clear
C)
\[y=2x+10\]
done
clear
D)
\[y=2x-12\]
done
clear
View Answer play_arrow
question_answer 251) If (2, 3, 5) is one end of a diameter of the sphere\[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x-12y-2z+20=0,\]then the coordinates of the other end of the diameter are
A)
\[(4,\text{ }3,\text{ }5)\]
done
clear
B)
\[(4,9,-3)\]
done
clear
C)
\[(4,\text{ }3,-3)\]
done
clear
D)
\[(4,-9,3)\]
done
clear
View Answer play_arrow
question_answer 252) If\[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{0},|\overrightarrow{a}|=3,|\overrightarrow{b}|=5,|\overrightarrow{c}|=7,\]then angle between a and b is
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{2\pi }{3}\]
done
clear
C)
\[\frac{5\pi }{3}\]
done
clear
D)
\[\frac{\pi }{3}\]
done
clear
View Answer play_arrow
question_answer 253) If\[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\]are three unit vectors,\[\overrightarrow{b}\ne \overrightarrow{c}\]and \[\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})=\frac{1}{2}\overrightarrow{b},\] then angle between\[\overrightarrow{a}\]and\[\overrightarrow{c}\]is
A)
\[\frac{\pi }{6}\]
done
clear
B)
\[\frac{\pi }{3}\]
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
question_answer 254) The roots of the equation\[a{{x}^{2}}+bx+c=0\]are \[\alpha ,\beta \]and roots of\[A{{x}^{2}}+Bx+C=0\]are \[\alpha -k,\beta -k,\]then the value of\[\frac{({{B}^{2}}-4AC)}{({{b}^{2}}-4ac)}\]is
A)
\[{{\left( \frac{A}{a} \right)}^{2}}\]
done
clear
B)
\[x\le 0\]
done
clear
C)
\[0\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 255) The value of\[x\]which satisfied the in equation \[{{x}^{3}}+1>{{x}^{2}}+x,\]is:
A)
\[x\ge 0\]
done
clear
B)
\[x\le 0\]
done
clear
C)
\[x\ge -1\]
done
clear
D)
\[-1\le x\le 1\]
done
clear
View Answer play_arrow
question_answer 256) If\[\frac{1}{q+r},\frac{1}{r+p},\frac{1}{p+q}\]are in AP, then
A)
\[p,q,r\]will be in AP
done
clear
B)
\[\frac{1}{p},\frac{1}{q},\frac{1}{r}\]will be in AP
done
clear
C)
\[{{p}^{2}},{{q}^{2}},{{r}^{2}}\]will be in AP
done
clear
D)
\[\frac{1}{{{p}^{2}}},\frac{1}{{{q}^{2}}},\frac{1}{{{r}^{2}}}\]will be in AP
done
clear
View Answer play_arrow
question_answer 257) The roots of the equation\[{{x}^{2}}-3x+a=0\]are\[\alpha ,\beta \] and roots of the equation \[{{x}^{2}}-12x+b=0\]are\[\gamma ,\delta \]and\[\alpha ,\beta ,\gamma ,\delta \]are in GP, then
A)
\[a=2,b=32\]
done
clear
B)
\[a=3,b=12\]
done
clear
C)
\[a=4,b=16\]
done
clear
D)
\[a=12,b=3\]
done
clear
View Answer play_arrow
question_answer 258) The sum of the infinite terms of the series\[1+\frac{4}{5}+\frac{7}{{{5}^{2}}}+\frac{10}{{{5}^{3}}}+...\]is
A)
\[\frac{16}{35}\]
done
clear
B)
\[\frac{11}{8}\]
done
clear
C)
\[\frac{35}{16}\]
done
clear
D)
\[\frac{9}{16}\]
done
clear
View Answer play_arrow
question_answer 259) If\[x,2x+2,3x+3,...\]are in GP, then fourth term of this series is
A)
13.5
done
clear
B)
\[-13.5\]
done
clear
C)
27
done
clear
D)
\[-27\]
done
clear
View Answer play_arrow
question_answer 260) The number of total terms in the expansion of\[{{(1+3\sqrt{2}x)}^{9}}+{{(1-3\sqrt{2}x)}^{9}}\]is
A)
9
done
clear
B)
0
done
clear
C)
5
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 261) The value of\[\frac{1+\frac{1}{2!}+\frac{2}{3!}+\frac{{{2}^{2}}}{4!}+\frac{{{2}^{3}}}{5!}+.....}{1+\frac{1}{2!}+\frac{1}{4!}+\frac{1}{6!}+...}\]is
A)
\[\frac{e}{4}\]
done
clear
B)
\[\frac{e}{2}\]
done
clear
C)
\[8e\]
done
clear
D)
\[\frac{e({{e}^{2}}-1)}{2({{e}^{2}}+1)}\]
done
clear
View Answer play_arrow
question_answer 262) If n is a multiple of 3, then coefficient of\[{{x}^{n}}\]in the expansion of\[log(1+x+{{x}^{2}})\]is (where\[|x|<2\])
A)
\[-\frac{2}{n}\]
done
clear
B)
\[-\frac{1}{n}\]
done
clear
C)
\[\frac{1}{n}\]
done
clear
D)
\[\frac{2}{n}\]
done
clear
View Answer play_arrow
question_answer 263) If a, b, c are different positive numbers, then the value of\[(b+ca)(c+a-b)(a+b-c)\]\[-abc\]will be
A)
positive
done
clear
B)
negative
done
clear
C)
zero
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 264) If set A have 10 elements, then the number of relations from A to A is
A)
\[10!\]
done
clear
B)
\[{{10}^{10}}\]
done
clear
C)
\[{{2}^{10}}\]
done
clear
D)
\[{{2}^{10}}-1\]
done
clear
View Answer play_arrow
question_answer 265) If two dice are thrown together. Probability that the sum of the numbers appearing on them is 7, is
A)
\[\frac{5}{36}\]
done
clear
B)
\[\frac{1}{6}\]
done
clear
C)
\[\frac{7}{36}\]
done
clear
D)
\[\frac{8}{36}\]
done
clear
View Answer play_arrow
question_answer 266) If \[A=\left[ \begin{matrix} 1 & 2 \\ 3 & -5 \\ \end{matrix} \right],B=\left[ \begin{matrix} 1 & 0 \\ 0 & 2 \\ \end{matrix} \right]\]and X is a matrix such that\[A=BX,\]then the value of X is
A)
\[\left[ \begin{matrix} 2 & 4 \\ 3 & -5 \\ \end{matrix} \right]\]
done
clear
B)
\[\frac{1}{2}\left[ \begin{matrix} 2 & 4 \\ 3 & -5 \\ \end{matrix} \right]\]
done
clear
C)
\[\left[ \begin{matrix} -2 & 4 \\ 3 & 5 \\ \end{matrix} \right]\]
done
clear
D)
\[\frac{1}{2}\left[ \begin{matrix} -2 & 4 \\ 3 & 5 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
question_answer 267) The system of equations\[x+2y+3z=1,\]\[2x+y+3z=2,\]\[5x+5y+9z=4\]have
A)
no solution is possible
done
clear
B)
only one solution
done
clear
C)
infinite solutions
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 268) If\[{{\left| \begin{matrix} 4 & 1 \\ 2 & 1 \\ \end{matrix} \right|}^{2}}=\left| \begin{matrix} 3 & 2 \\ 1 & x \\ \end{matrix} \right|-\left| \begin{matrix} x & 3 \\ -2 & 1 \\ \end{matrix} \right|,\]then the value of\[x\]is
A)
6
done
clear
B)
7
done
clear
C)
8
done
clear
D)
11
done
clear
View Answer play_arrow
question_answer 269) If\[\left| \begin{matrix} a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x \\ \end{matrix} \right|=0,\]then the values of \[x\]will be
A)
\[x=0,x=4a\]
done
clear
B)
\[x=0,x=a\]
done
clear
C)
\[x=0,\text{ }x=2a\]
done
clear
D)
\[x=0,\text{ }x=3a\]
done
clear
View Answer play_arrow
question_answer 270) If\[\Sigma x=15,\Sigma y=40,\Sigma xy=110\]and\[n=5,\]then the value of cov\[(x,y)\]is
A)
\[-2\]
done
clear
B)
2
done
clear
C)
22
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 271) If\[f:N\to R,f(x)=\frac{(2x-1)}{2}\]and\[g:Q\to R,g(x)=x+2\]are two functions, then the value of\[(gof)\left( \frac{3}{2} \right)\]is
A)
1
done
clear
B)
3
done
clear
C)
\[\frac{7}{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 272) The value of\[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt{\left[ \frac{1}{2}(1-\cos 2x) \right]}}{x}\]is
A)
1
done
clear
B)
\[-1\]
done
clear
C)
0
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 273) If function \[f(x)=\left\{ \begin{matrix} \frac{\sqrt{(1+px)}-\sqrt{(1-px)}}{x}, & x<0 \\ \frac{2x+1}{x-2} & ,0\le x\le 1 \\ \end{matrix} \right.\] is continuous in the interval\[[-1,1],\]then the value of p is
A)
\[-1\]
done
clear
B)
\[-1/2\]
done
clear
C)
1/2
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 274) If\[y=\log |x|\]and\[x\ne 0,\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{1}{x}\]
done
clear
B)
\[-\frac{1}{x}\]
done
clear
C)
\[\frac{1}{|x|}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 275) If\[y={{\sin }^{-1}}\sqrt{(1-x)}+{{\cos }^{-1}}\sqrt{x},\]then\[\frac{dy}{dx}\]is equal to
A)
\[\frac{-1}{\sqrt{x(1-x)}}\]
done
clear
B)
\[\frac{1}{\sqrt{x(1+x)}}\]
done
clear
C)
\[\frac{1}{\sqrt{x(1-x)}}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 276) If\[y=b\cos \left\{ n\log \left( \frac{x}{n} \right) \right\},\]then which of the following is correct?
A)
\[{{x}^{2}}{{y}_{2}}+x{{y}_{1}}-{{n}^{2}}y=0\]
done
clear
B)
\[{{x}^{2}}{{y}_{2}}-x{{y}_{1}}-{{n}^{2}}y=0\]
done
clear
C)
\[{{x}^{2}}{{y}_{2}}+x{{y}_{1}}+{{n}^{2}}y=0\]
done
clear
D)
\[{{x}^{2}}{{y}_{2}}-x{{y}_{1}}+{{n}^{2}}y=0\]
done
clear
View Answer play_arrow
question_answer 277) If tangent to the curve\[x=a{{t}^{2}},\text{ }y=2at\]is perpendicular to\[x-\]axis, then point of contact is
A)
(0, 0)
done
clear
B)
(0, a)
done
clear
C)
(a, 0)
done
clear
D)
(a, a)
done
clear
View Answer play_arrow
question_answer 278) The equation of ellipse whose vertex is (±5,0) and focus is (±4,0), is
A)
\[9{{x}^{2}}+25{{y}^{2}}=225\]
done
clear
B)
\[25{{x}^{2}}+9{{y}^{2}}=225\]
done
clear
C)
\[3{{x}^{2}}+4{{y}^{2}}=192\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 279) The value of\[\int{\frac{dx}{{{e}^{x}}+{{e}^{-x}}}}\]is
A)
\[{{\tan }^{-1}}({{e}^{x}})+c\]
done
clear
B)
\[\log ({{e}^{x}}+{{e}^{-x}})+c\]
done
clear
C)
\[\log ({{e}^{2x}}+1)+c\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 280) The value of\[\int{{{e}^{x}}\left\{ \frac{(x-1)}{{{(x+1)}^{3}}} \right\}}dx\]is
A)
\[\frac{{{e}^{x}}}{{{(x+1)}^{2}}}+c\]
done
clear
B)
\[\frac{{{e}^{x}}}{(x+1)}+c\]
done
clear
C)
\[\frac{-{{e}^{x}}}{(x+1)}+c\]
done
clear
D)
\[\frac{-{{e}^{x}}}{{{(x+1)}^{2}}}+c\]
done
clear
View Answer play_arrow
question_answer 281) The value of\[\int_{-\pi /2}^{\pi /2}{\log \left( \frac{2-\sin \theta }{2+\sin \theta } \right)dx}\]is
A)
0
done
clear
B)
1
done
clear
C)
2
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 282) The value of\[\int_{0}^{\pi /4}{\log (1+\tan x)dx}\]is
A)
\[\frac{1}{2}\pi \log 8\]
done
clear
B)
\[\frac{1}{4}\pi \log 2\]
done
clear
C)
\[\frac{1}{8}\pi \log 2\]
done
clear
D)
\[\frac{1}{4}\pi \log 8\]
done
clear
View Answer play_arrow
question_answer 283) The maximum value of\[f(x)=\int_{1}^{x}{|t|}\,dt\]in the interval\[\left[ -\frac{1}{2},\frac{1}{2} \right]\]is
A)
\[-\frac{1}{2}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[-\frac{5}{8}\]
done
clear
D)
\[\frac{3}{8}\]
done
clear
View Answer play_arrow
question_answer 284) The area of the region bounded by the curve \[y=4+3x-{{x}^{2}}\]and\[x-\]axis is
A)
\[\left( \frac{125}{3} \right)sq\,units\]
done
clear
B)
\[\left( \frac{125}{6} \right)sq\,units\]
done
clear
C)
\[\left( \frac{125}{4} \right)sq\,units\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 285) If the area of the region bounded by the curve \[y=8{{x}^{2}}-{{x}^{5}},\]straight line\[x=0\]and\[x=a\]and the\[x-\]axis is\[\frac{16}{3},\]then the value of a is
A)
\[{{(8-4\sqrt{2})}^{1/3}}\]
done
clear
B)
\[{{(8+\sqrt{2})}^{1/3}}\]
done
clear
C)
no value of\[a\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 286) The solution of the differential equation\[{{x}^{2}}dy+y(x+y)dx=0\]is
A)
\[y+2x=\frac{{{c}^{2}}{{x}^{2}}}{y}\]
done
clear
B)
\[y-2x=\frac{{{c}^{2}}{{x}^{2}}}{y}\]
done
clear
C)
\[y+2x={{c}^{2}}{{x}^{2}}y\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 287) The solution of the differential equation \[\frac{dy}{dx}+\frac{1}{x}\tan y=\frac{1}{{{x}^{2}}}\tan y\sin y\]is
A)
\[2x=\frac{(1+2c{{x}^{2}})}{\sin y}\]
done
clear
B)
\[2x=\sin y(1+2c{{x}^{2}})\]
done
clear
C)
\[2x+\sin y(1+c{{x}^{2}})=0\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 288) If\[{{\alpha }_{1}},{{\alpha }_{2}},....,{{\alpha }_{n-1}}\]are n roots of unity, then the value of\[(1-{{\alpha }_{1}})(1-{{\alpha }_{2}}).....(1-{{\alpha }_{n-1}})\]is
A)
\[n\]
done
clear
B)
\[n-1\]
done
clear
C)
\[-1\]
done
clear
D)
\[1\]
done
clear
View Answer play_arrow
question_answer 289) If\[\left| \frac{({{z}_{1}}-2{{z}_{2}})}{(2-{{z}_{1}}{{\overline{z}}_{2}})} \right|=1\]and\[|{{z}_{2}}|\ne 1,\]where\[{{z}_{1}}\]and\[{{z}_{2}}\]are complex numbers, then the value of\[|{{z}_{1}}|\]is
A)
1
done
clear
B)
\[-1\]
done
clear
C)
2
done
clear
D)
\[-2\]
done
clear
View Answer play_arrow
question_answer 290) The value of\[sin\text{ }20{}^\circ sin\text{ }40{}^\circ sin\text{ }60{}^\circ sin\text{ }80{}^\circ \]is:
A)
\[-\frac{3}{16}\]
done
clear
B)
\[\frac{3}{16}\]
done
clear
C)
\[-\frac{5}{16}\]
done
clear
D)
\[\frac{5}{16}\]
done
clear
View Answer play_arrow
question_answer 291) If\[A+B+C=\frac{\pi }{2},\]then the value of \[sin\text{ }2A+sin\text{ }2B+sin\text{ }2C\]is
A)
\[2\text{ }sin\text{ }A\text{ }sin\text{ }B\text{ }sin\text{ }C\]
done
clear
B)
\[2\text{ }cos\text{ }A\text{ }cos\,B\text{ }cos\text{ }C\]
done
clear
C)
\[4\text{ }sin\text{ }A\text{ }sin\text{ }B\text{ }sin\text{ }C\]
done
clear
D)
\[4\text{ }cos\text{ }A\text{ }cos\text{ B }cos\text{ }C\]
done
clear
View Answer play_arrow
question_answer 292) The period of\[sin4\text{ }x+cos4\text{ }x\]is
A)
\[\pi \]
done
clear
B)
\[\frac{\pi }{2}\]
done
clear
C)
\[2\pi \]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 293) In the interval\[0<x<2\pi ,\]the solution of \[(2\text{ }cos\text{ }x-1)(3+2\text{ }cos\text{ }x)=0\]is
A)
\[\left\{ \frac{\pi }{3} \right\}\]
done
clear
B)
\[\left\{ \frac{\pi }{3},\frac{5\pi }{3} \right\}\]
done
clear
C)
\[\left\{ \frac{\pi }{3},\frac{5\pi }{3},{{\cos }^{-1}}\left( -\frac{3}{2} \right) \right\}\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
question_answer 294) If in the\[\Delta ABC,\angle A=30{}^\circ ,c=10,\angle C=90{}^\circ ,\]then the value of b is
A)
5
done
clear
B)
\[5\sqrt{3}\]
done
clear
C)
10
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 295) If\[{{\sin }^{-1}}\frac{x}{5}+\cos e{{c}^{-1}}\frac{5}{4}=\frac{\pi }{2},\]then the value of\[x\]is
A)
1
done
clear
B)
3
done
clear
C)
4
done
clear
D)
5
done
clear
View Answer play_arrow
question_answer 296) A line is perpendicular to the line\[3x+y=3\] and passes through the point\[(-2,2),\]then its intercept on y-axis is
A)
\[\frac{1}{3}\]
done
clear
B)
\[\frac{2}{3}\]
done
clear
C)
\[1\]
done
clear
D)
\[\frac{8}{3}\]
done
clear
View Answer play_arrow
question_answer 297) The locus of the foot of the perpendicular on the line\[\frac{x}{a}+\frac{y}{b}=1,\]where\[\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}=\frac{1}{{{c}^{2}}}\]from the origin, is
A)
\[{{x}^{2}}+{{y}^{2}}={{c}^{2}}\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}=2{{c}^{2}}\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}=\frac{c}{2}\]
done
clear
D)
None of these
done
clear
View Answer play_arrow
question_answer 298) The focus of parabola\[{{y}^{2}}=4y-4x\]is
A)
(0, 2)
done
clear
B)
(1, 2)
done
clear
C)
(2, 0)
done
clear
D)
(2, 1)
done
clear
View Answer play_arrow
question_answer 299) The focus of the hyperbola\[4{{x}^{2}}-9{{y}^{2}}-36=0\]are
A)
\[(\pm \sqrt{11},0)\]
done
clear
B)
\[(0,\pm \sqrt{12})\]
done
clear
C)
\[(\pm \sqrt{12},0)\]
done
clear
D)
\[(\pm \sqrt{13},0)\]
done
clear
View Answer play_arrow
question_answer 300) The equation of the tangent of the hyperbola \[2{{x}^{2}}-3{{y}^{2}}=6\]which is parallel to the line \[y=3x+4,\]is
A)
\[y=3x-5\]
done
clear
B)
\[y=3x+5\]
done
clear
C)
\[y=3x+5\]and\[y=3x-5\]
done
clear
D)
None of the above
done
clear
View Answer play_arrow
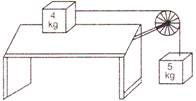
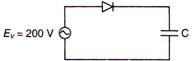
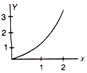
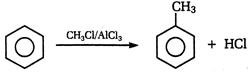 The above reaction is called
The above reaction is called
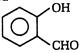 \[+3KCl+{{H}_{2}}O\]
\[+3KCl+{{H}_{2}}O\]
