
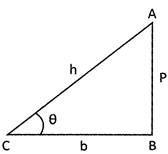
 Then the trigonometrical ratios are defined as follows:
\[\sin \theta =\frac{\text{Perpendicual}}{\text{Hypotenuse}}=\frac{AB}{AC}\]
\[\cos \theta =\frac{Base}{\text{Hypotenuse}}=\frac{BC}{AC}\]
\[\tan \theta =\frac{\text{Perpendicular}}{Base}=\frac{AB}{BC}\]
\[\cot \theta =\frac{Base}{\text{Perpendicular}}=\frac{BC}{AB}\]
\[\sec \theta =\frac{\text{Hypotenuse}}{Base}=\frac{AC}{BC}\]
\[co\sec \theta =\frac{\text{Hypotenuse}}{\text{Perpendicular}}=\frac{AC}{AB}\] AB
If we represent perpendicular, base and hypotenuse by P, b and h respectively then the ratios can be written as:
Then the trigonometrical ratios are defined as follows:
\[\sin \theta =\frac{\text{Perpendicual}}{\text{Hypotenuse}}=\frac{AB}{AC}\]
\[\cos \theta =\frac{Base}{\text{Hypotenuse}}=\frac{BC}{AC}\]
\[\tan \theta =\frac{\text{Perpendicular}}{Base}=\frac{AB}{BC}\]
\[\cot \theta =\frac{Base}{\text{Perpendicular}}=\frac{BC}{AB}\]
\[\sec \theta =\frac{\text{Hypotenuse}}{Base}=\frac{AC}{BC}\]
\[co\sec \theta =\frac{\text{Hypotenuse}}{\text{Perpendicular}}=\frac{AC}{AB}\] AB
If we represent perpendicular, base and hypotenuse by P, b and h respectively then the ratios can be written as:
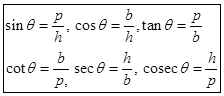 Relationship between Ratios
Relationship between Ratios
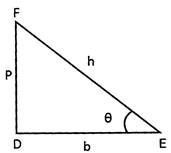 In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are
1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]
We can also derive different relations between identities in different form
(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]
or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]
Similarly
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]
(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]
Similarly
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
or \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]
(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
or \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]
or \[\cos e{{c}^{2}}\theta more...
In the adjoining figure triangle DEF is a right angled triangle right angle at D. Then the trigonometrical identities are
1. \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
2. \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
3. \[co{{\sec }^{2}}\theta -{{\cot }^{2}}\theta =1\]
We can also derive different relations between identities in different form
(a) \[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
or \[{{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \]
or \[\sin \theta =\pm \sqrt{1-{{\cos }^{2}}\theta }\]
Similarly
\[{{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
or \[\cos \theta =\pm \sqrt{1-{{\sin }^{2}}\theta }\]
(b) \[{{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1\]
or \[{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \]
or \[{{\sec }^{2}}\theta =\sqrt{1+{{\tan }^{2}}\theta }\]
Similarly
\[{{\tan }^{2}}\theta ={{\sec }^{2}}\theta -1\]
or \[\tan \theta =\pm \sqrt{{{\sec }^{2}}\theta -1}\]
(c) \[\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1\]
or \[\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta \]
or \[\cos e{{c}^{2}}\theta more...
| Quadrant\[\to \] Ratios \[\downarrow \] | I | II | III | IV |
| \[\sin \theta \] | + | + | more...
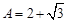 more... more...
Articles CategoriesArchive
Trending Articles
You need to login to perform this action. |