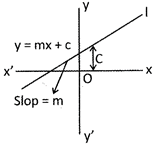
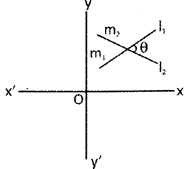
 If the lines are perpendicular, then \[{{m}_{1}}{{m}_{2}}=-1\] and if the lines are parallel then \[{{m}_{1}}{{m}_{2}}\]
If the lines are perpendicular, then \[{{m}_{1}}{{m}_{2}}=-1\] and if the lines are parallel then \[{{m}_{1}}{{m}_{2}}\]

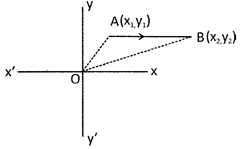
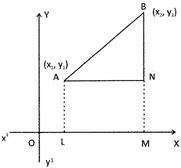 Now, from Figure
\[OL={{X}_{1}},OM={{X}_{2}},AL={{Y}_{1}}\And BM={{Y}_{2}}\].
\[\therefore \,\,\,AN=LM=(OM-OL)={{X}_{2}}-{{X}_{1}}\]
BN = (BM - NM) = (BM - AL) \[={{Y}_{2}}-{{Y}_{1}}\,\,[\therefore \,NM=AL]\]
From right \[\Delta ANB\], By Pythagorean" theorem, we have \[A{{B}^{2}}=(A{{N}^{2}}+B{{M}^{2}})\]
\[\Rightarrow \,\,{{(AB)}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}\]
\[\Rightarrow \,\,(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Hence, the distance between the points \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] given by:
\[(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Section Formula
Let us consider the point P(X, Y) which divides the line segment joining \[A({{x}_{1}},{{x}_{1}})\And B({{x}_{2}}-{{y}_{2}})\] in the ratio m : n, then the coordinate of the point P is given by:
\[X=\frac{m{{x}_{1}}n{{x}_{2}}}{m+n}and\,\,y=\frac{m{{y}_{1}}+n{{y}_{2}}}{m+n}\]
Proof
Let \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\]be the two points and let P(X, Y) divides it in the ratio m:n, then,
\[\frac{AP}{PB}=\frac{m}{n}\]
Now, from Figure
\[OL={{X}_{1}},OM={{X}_{2}},AL={{Y}_{1}}\And BM={{Y}_{2}}\].
\[\therefore \,\,\,AN=LM=(OM-OL)={{X}_{2}}-{{X}_{1}}\]
BN = (BM - NM) = (BM - AL) \[={{Y}_{2}}-{{Y}_{1}}\,\,[\therefore \,NM=AL]\]
From right \[\Delta ANB\], By Pythagorean" theorem, we have \[A{{B}^{2}}=(A{{N}^{2}}+B{{M}^{2}})\]
\[\Rightarrow \,\,{{(AB)}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}\]
\[\Rightarrow \,\,(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Hence, the distance between the points \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] given by:
\[(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Section Formula
Let us consider the point P(X, Y) which divides the line segment joining \[A({{x}_{1}},{{x}_{1}})\And B({{x}_{2}}-{{y}_{2}})\] in the ratio m : n, then the coordinate of the point P is given by:
\[X=\frac{m{{x}_{1}}n{{x}_{2}}}{m+n}and\,\,y=\frac{m{{y}_{1}}+n{{y}_{2}}}{m+n}\]
Proof
Let \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\]be the two points and let P(X, Y) divides it in the ratio m:n, then,
\[\frac{AP}{PB}=\frac{m}{n}\]
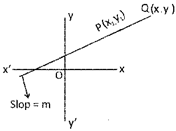
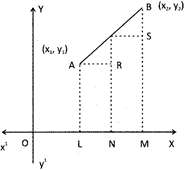 Draw \[AL\bot OX;BM\bot OX;PN\bot OX,AR\bot PN,\And PS\bot \]BM.
Now, \[AR=LM=ON=OL=({{x}_{1}}-{{x}_{2}})\]
\[PS=NM=OM=ON=({{x}_{2}}-x)\]
\[PR=PN-RN=PN-AL=(y-{{y}_{1}})\]
\[BS=MB-SM=BM-PN=({{y}_{2}}-y)\]
Clearly \[\Delta ARP\,and\,\Delta PSB\] are similar & their sides are in proportional.
\[\therefore \,\,\,\,\,\frac{AP}{PB}=\frac{AR}{PS}=\frac{PR}{BS}\]
\[\Rightarrow \,\,\,\,\,\frac{m}{n}=\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{2}}}{{{y}_{2}}-y}\]
\[\Rightarrow \,\,\,\,x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Hence the coordinate of the point \[P\left( x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
Draw \[AL\bot OX;BM\bot OX;PN\bot OX,AR\bot PN,\And PS\bot \]BM.
Now, \[AR=LM=ON=OL=({{x}_{1}}-{{x}_{2}})\]
\[PS=NM=OM=ON=({{x}_{2}}-x)\]
\[PR=PN-RN=PN-AL=(y-{{y}_{1}})\]
\[BS=MB-SM=BM-PN=({{y}_{2}}-y)\]
Clearly \[\Delta ARP\,and\,\Delta PSB\] are similar & their sides are in proportional.
\[\therefore \,\,\,\,\,\frac{AP}{PB}=\frac{AR}{PS}=\frac{PR}{BS}\]
\[\Rightarrow \,\,\,\,\,\frac{m}{n}=\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{2}}}{{{y}_{2}}-y}\]
\[\Rightarrow \,\,\,\,x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Hence the coordinate of the point \[P\left( x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
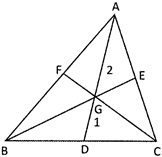 Let G (x, y) be the centroid of A ABC.
Then, G divides AD in the ratio 2 : 1.
\[\therefore \,\,\,\,x=\left\{ \frac{2\frac{({{x}_{2}}+{{x}_{3}})}{2}+1.{{x}_{1}}}{2+1} \right\}=\frac{({{x}_{1}}+{{x}_{2}}+{{x}_{3}})}{3}\]
\[y=\left\{ \frac{2\frac{({{y}_{2}}+{{y}_{3}})}{2}+1.{{y}_{3}}}{2+1} \right\}=\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3}\]
Hence the coordinates of G are \[\left( \frac{({{x}_{1}}+{{x}_{2}}{{+}_{3}}}{3},\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3} \right)\].
Let G (x, y) be the centroid of A ABC.
Then, G divides AD in the ratio 2 : 1.
\[\therefore \,\,\,\,x=\left\{ \frac{2\frac{({{x}_{2}}+{{x}_{3}})}{2}+1.{{x}_{1}}}{2+1} \right\}=\frac{({{x}_{1}}+{{x}_{2}}+{{x}_{3}})}{3}\]
\[y=\left\{ \frac{2\frac{({{y}_{2}}+{{y}_{3}})}{2}+1.{{y}_{3}}}{2+1} \right\}=\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3}\]
Hence the coordinates of G are \[\left( \frac{({{x}_{1}}+{{x}_{2}}{{+}_{3}}}{3},\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3} \right)\].
| Coordinate | I | II | III | IV | V | VI | VII | VIII | |||||||||||||||
| X | + | - | - | + | + | - | - | more...
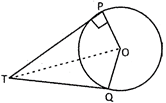 \[\angle OPT=\angle OQT={{90}^{o}},\,\angle POT=\angle QOT\] \[\angle QTO=\angle OTP\,and\,PT\,=\,QT\]
\[\angle OPT=\angle OQT={{90}^{o}},\,\angle POT=\angle QOT\] \[\angle QTO=\angle OTP\,and\,PT\,=\,QT\]
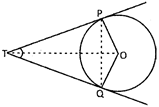 (a) \[\angle QTP=\angle QPO\]
(b) \[\angle QTP=2\angle QPO\]
(c) \[\angle QTP=3\angle QPO\]
(d) \[\angle QTP={{90}^{o}}\]
(e) None of these
Answer: (b)
Explanation
In the given figure, we have
TP = TO. [tangents drawn from an external point are equal in length]
\[\Rightarrow \,\,\angle TPQ=\,\angle TPQ\]
\[In\,\angle QTQ,\,we\,\,have\]
\[\angle TPQ+\angle TQP+PTQ={{180}^{o}}\]
\[\Rightarrow \,\angle TPQ={{90}^{o}}-\frac{1}{2}\angle PTQ\]
\[\Rightarrow \,\frac{1}{2}\angle PTQ={{90}^{o}}-\angle TPQ\] .... (i)
Also, \[\angle OPT={{90}^{o}}\]
\[\Rightarrow \,\angle OPQ={{90}^{o}}-\angle TPQ\] .... (ii)
From (i) and (ii), we get
\[\frac{1}{2}\angle PTQ=\angle OPQ\Rightarrow \angle PTQ=2\angle OPQ\]
(a) \[\angle QTP=\angle QPO\]
(b) \[\angle QTP=2\angle QPO\]
(c) \[\angle QTP=3\angle QPO\]
(d) \[\angle QTP={{90}^{o}}\]
(e) None of these
Answer: (b)
Explanation
In the given figure, we have
TP = TO. [tangents drawn from an external point are equal in length]
\[\Rightarrow \,\,\angle TPQ=\,\angle TPQ\]
\[In\,\angle QTQ,\,we\,\,have\]
\[\angle TPQ+\angle TQP+PTQ={{180}^{o}}\]
\[\Rightarrow \,\angle TPQ={{90}^{o}}-\frac{1}{2}\angle PTQ\]
\[\Rightarrow \,\frac{1}{2}\angle PTQ={{90}^{o}}-\angle TPQ\] .... (i)
Also, \[\angle OPT={{90}^{o}}\]
\[\Rightarrow \,\angle OPQ={{90}^{o}}-\angle TPQ\] .... (ii)
From (i) and (ii), we get
\[\frac{1}{2}\angle PTQ=\angle OPQ\Rightarrow \angle PTQ=2\angle OPQ\]
In this chapter we will discuss about the similarity of triangles. Two figures having the same shape and not necessarily the same size are called the similar figures. Two polygons of the same number of sides are similar if their corresponding angles are equal and their corresponding sides are in the same ratio.
We are familiar with some of the basic solids like cuboid, cone, cylinder, and sphere. In this chapter we will discuss about how to find the surface area and volume of these figures in our daily life, we come across number of solids made up of combinations of two or more of the basic solids.
|