
Condition for Consistency
For the system of linear equation\[{{a}_{1}}x+{{b}_{1}}y={{c}_{1}}\,and\,{{a}_{2}}x+{{b}_{2}}\,y={{c}_{2}}\],
If \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\], then the system of equation has unique solution.
If \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\], then the system of equation has no solution.
If \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\] then the system of equation has infinitely many solution.


The types of solution the pair of linear equation \[3x+4y=7\, and \,4x-3y=7\] have?
(a) Unique solution
(b) No solution
(c) Infinitely many solution
(d) All of these
(e) None of these
Answer: (a)

Which one of the following is the condition for infinitely many solution?
(a) \[{{a}_{1}}{{a}_{2}}={{b}_{1}}{{b}_{2}}\]
(b) \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\]
(c) \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\]
(d) \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]
(e) None of these
Answer: (d)

The value of m for which the given system of equation \[mx-5y=10\, and \,8x=9y=24\] has no solution.
(a) \[\left( m\ne \frac{40}{9}\And m=\frac{10}{3} \right)\]
(b) \[\left( m=\frac{40}{9}\And m\ne \frac{10}{3} \right)\]
(c) \[\left( m=\frac{40}{9}\And m=\frac{10}{3} \right)\]
(d) \[\left( m\ne \frac{40}{9}\And m\ne \frac{10}{3} \right)\]
(e) None of these
Answer: (b)

Find the relation between m and n for which the system of equation \[4x+6y=14\, and \,(m+n)x+(2m-n)y=21\], has unique solution.
(a) 2m = 3n
(b) m = 5n
(c) \[2m\ne 3n\]
(d) \[m\ne 5n\]
(e) None of these
Answer: (d)

The ratio of income of Mack and Jacob is 3 : 4 and the ratio of their expenditure is 1: 2. If their individual saving is Rs. 2000, then their monthly income is:
(a) (Rs. 3000 & Rs. 4000)
(b) (Rs. 2000 & Rs. 3000)
(c) (Rs. 4000 & Rs. 6000)
(d) (Rs. 1000 & Rs. 4000)
(e) None of these
Answer: (a)


Cross Multiplication Method

Solve the system of equations \[2x+3y=17,3x-2y=6\] by the method of cross multiplication.
(a) \[X=4\And y=-3\]
(b) \[X=2\And y=-5\]
(c) \[X=-4\And y=1\]
(d) \[X=-5\And y=7\]
(e) None of these
Answer: (a)
Explanation
By cross multiplication, we have
\[\therefore \,\,\frac{x}{\left[ 3\times (-6)-(-2)\times (-17) \right]}=\frac{y}{\left[ (-17)\times 3-(-6)\times 2 \right]}=\frac{1}{\left[ 2\times (-2)-3\times 3 \right]}\] \[\Rightarrow \,\,\,\frac{x}{(-18-34)}=\frac{y}{(-51+12)}=\frac{1}{(-4-9)}\]
\[\Rightarrow \,\,\,\frac{x}{(-52)}=\frac{y}{(-39)}=\frac{1}{(-13)}=3\]
\[\Rightarrow \,\,x=\,\frac{-52}{-13}=4,y=\frac{-39}{13}=3\]
Hence, \[x=4\And y=3\] is the required solution

Solve the system of equation by cross multiplication method.
\[4x-7y+28=0\]
\[5y-7x+9=0\]
(a) \[x=6\And y=3\]
(b) \[x=2\And y=8\]
(c) \[x=7\And y=8\]
(d) \[x=7\And y=7\]
(e) None of these
Answer: (c)
By cross multiplication, we have
\[\therefore \,\,\,\,\frac{x}{\left[ (-7)\times 9-5\times 28 \right]}=\frac{y}{\left[ 28\times (-7)-9\times 4 \right]}=\frac{1}{\left[ 4\times 5-(-7)\times (-7) \right]}\]\[\Rightarrow \,\,\frac{x}{(-63-140)}=\frac{y}{(-196-36)}=\frac{1}{20-49}\]
\[\Rightarrow \,\,\frac{x}{-203}=\frac{y}{-232}=\frac{1}{-29}\]
\[\Rightarrow \,\,x=\left( \frac{-203}{-29} \right)=7\And y=\left( \frac{-232}{-29} \right)=8\] Hence, x = 7 & y = 8 is the
more...
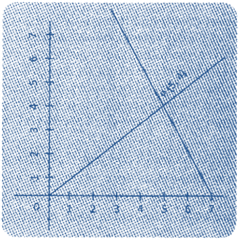
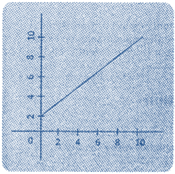
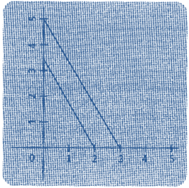


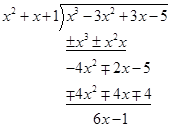
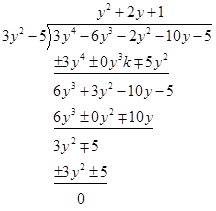

 (2) Infinitely Many Solutions
If the graph of the pair of linear equation is coincident, then the system of linear equation is said to have infinitely many solutions.
\[y=3x+2\,and\,6x-2y+4=0\]
(2) Infinitely Many Solutions
If the graph of the pair of linear equation is coincident, then the system of linear equation is said to have infinitely many solutions.
\[y=3x+2\,and\,6x-2y+4=0\]
 (B) Inconsistent Equation
It has only one type of solution, which is no solution.
(1) No Solution
If the graph of the system of equation is parallel and does not intersect each other at any point, then it is said to have no solution.
\[3x+3y=15\]
\[2y=-2x+6\]
(B) Inconsistent Equation
It has only one type of solution, which is no solution.
(1) No Solution
If the graph of the system of equation is parallel and does not intersect each other at any point, then it is said to have no solution.
\[3x+3y=15\]
\[2y=-2x+6\]

 Solve the system of the equation given by \[\frac{4}{16x+24z}+\frac{12}{21x-14z}=\frac{1}{2}\] and \[\frac{14}{4x+6z}+\frac{4}{(3x-2z)}=2\]
(a) \[(x=2,z=1)\]
(b) \[(x=3,z=5)\]
(c) \[(x=-4,z=1)\]
(d) \[(x=1,z=-1)\]
(e) None of these
Answer: (a)
Solve the system of the equation given by \[\frac{4}{16x+24z}+\frac{12}{21x-14z}=\frac{1}{2}\] and \[\frac{14}{4x+6z}+\frac{4}{(3x-2z)}=2\]
(a) \[(x=2,z=1)\]
(b) \[(x=3,z=5)\]
(c) \[(x=-4,z=1)\]
(d) \[(x=1,z=-1)\]
(e) None of these
Answer: (a)


