question_answer 1) If masses of all molecules of a gas are halved and their speeds are doubled, then the ratio of initial and final pressures is:
A)
1:2
done
clear
B)
2 : 1
done
clear
C)
4 : 1
done
clear
D)
1 : 4
done
clear
View Answer play_arrow
question_answer 2) A force \[\therefore \]N displaces the body by \[{{\upsilon }^{2}}=4rg\]in 2 sec. Power generated will be :
A)
11 watt
done
clear
B)
6 watt
done
clear
C)
22 watt
done
clear
D)
12 watt
done
clear
View Answer play_arrow
question_answer 3) A body moving with uniform acceleration describes 40 m in the first 5 sec and 65 m in next 5 sec. Its initial velocity will be :
A)
4 m/s
done
clear
B)
2.5 m/s
done
clear
C)
5.5 m/s
done
clear
D)
11 m/s
done
clear
View Answer play_arrow
question_answer 4) The displacement time graph for two bodies A and B are straight lines inclined at 30° and 60° respectively with the time axes. If \[\upsilon =\sqrt{4rg}\] and \[\upsilon =\sqrt{4\times 2.5\times 9.8}\] are their velocities, then \[\upsilon =\sqrt{98}\,\,m/s\]will be :
A)
\[\text{2}0\text{ g }=\text{ 2}\times \text{1}{{0}^{-\text{2}}}\text{ kg},\]
done
clear
B)
\[=\frac{360\times 5}{18}=100m/s\]
done
clear
C)
3 : 1
done
clear
D)
1 : 3
done
clear
View Answer play_arrow
question_answer 5) The first excited state of hydrogen atom is 10.2 eV above its ground state. The temperature needed to excite hydrogen atoms to first excited level, is :
A)
\[=\frac{n\times \frac{1}{2}m{{\upsilon }^{2}}}{t}\]
done
clear
B)
\[=\frac{360\times \frac{1}{2}\times 2\times {{10}^{-2}}\times {{(100)}^{2}}}{60}\]
done
clear
C)
\[g=\frac{Gm}{{{R}^{2}}}\]
done
clear
D)
\[\overrightarrow{\text{F}}=\left( \text{2\hat{i}}+\text{4\hat{j}} \right)\]
done
clear
View Answer play_arrow
question_answer 6) The acceleration of a train travelling with speed of 400 m/s as it goes round a curve of radius 160 m, is :
A)
\[\overrightarrow{S}=\left( \text{3\hat{j}}+\text{5\hat{k}} \right)\text{m}\]
done
clear
B)
\[{{\upsilon }_{A}}\]
done
clear
C)
\[{{\upsilon }_{B}}\]
done
clear
D)
\[{{\upsilon }_{A}}:{{\upsilon }_{B}}\]
done
clear
View Answer play_arrow
question_answer 7) The maximum and minimum tensions in the string whirling in a circle of radius 2.5 m are in the ratio 5:3 then its velocity is :
A)
\[\sqrt{3}:1\]
done
clear
B)
7 m/s
done
clear
C)
\[1:\sqrt{3}\]
done
clear
D)
\[7.9\times {{10}^{4}}K\]
done
clear
View Answer play_arrow
question_answer 8) From an automatic gun a man fires 360 bullets per minute with a speed of 360 km/hour. If each weighs 20 g, the power of the gun is :
A)
600 W
done
clear
B)
300 W
done
clear
C)
150 W
done
clear
D)
75 W
done
clear
View Answer play_arrow
question_answer 9) A body has a weight 90 kg on the earths surface, the mass of the moon is 1/9 that of the earths mass and its radius is ½ that of the earths radius. On the moon the weight of the body is:
A)
45 kg
done
clear
B)
202.5 kg
done
clear
C)
90 kg
done
clear
D)
40 kg
done
clear
View Answer play_arrow
question_answer 10) The amplitude of a particle executing SHM is 4 cm. At the mean position the speed of the particle is 16 cm/sec. The distance of the particle from the mean position at which the speed of the particle becomes \[3.5\times {{10}^{4}}K\] cm/s, will be :
A)
\[5.8\times {{10}^{4}}K\]
done
clear
B)
\[\text{14 }\times \,\,\text{1}{{0}^{\text{4}}}\text{ K}\]
done
clear
C)
1 cm
done
clear
D)
2 cm
done
clear
View Answer play_arrow
question_answer 11) The viscous force acting on a rain drop of radius 0.35 mm falling through air with a velocity of 1 m/s, is \[\text{1 km}/{{\text{s}}^{\text{2}}}\]
A)
\[\text{1}00\text{ m}/{{\text{s}}^{\text{2}}}\]
done
clear
B)
\[\text{1}0\text{ m}/{{\text{s}}^{\text{2}}}\]
done
clear
C)
\[\text{1}\,\text{m}/{{\text{s}}^{\text{2}}}\]
done
clear
D)
\[\sqrt{98}m/s\]
done
clear
View Answer play_arrow
question_answer 12) Two narrow capillary tubes A and B are of lengths ( and 111 and of same radius r. The rate of flow of water through the tube A under a constant pressure head P is 3\[\sqrt{\text{49}0}\text{ m}/\text{s}\]. If A and B are connected in series and the same pressure difference P is maintained between the ends of the composite tube, then the rate of flow of water is :
A)
\[\sqrt{\text{4}\text{.9}}\text{ m}/\text{s}\]
done
clear
B)
\[8\sqrt{3}\]
done
clear
C)
\[2\sqrt{3}cm\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 13) The energy of electron in the nth orbit of hydrogen atom is expressed as \[\sqrt{3}cm\]. The shortest and longest wavelength of Lyman series will be :
A)
\[\left( \eta =\text{2}\times \text{1}{{0}^{-\text{4}}}\text{Ns}/{{\text{m}}^{\text{2}}} \right):\]
done
clear
B)
\[6.6\times {{10}^{-6}}N\]
done
clear
C)
\[6.6\times {{10}^{-5}}N\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 14) Pitch of musical note depends on :
A)
its fundamental frequency only
done
clear
B)
its harmonics only
done
clear
C)
its amplitude only
done
clear
D)
the instrument producing the pitch
done
clear
View Answer play_arrow
question_answer 15) An electron is accelerated by a potential difference of 1000 volt. Its velocity will be :
A)
\[1.32\times {{10}^{-7}}N\]
done
clear
B)
\[13.2\times {{10}^{-7}}N\]
done
clear
C)
\[\text{c}{{\text{m}}^{\text{3}}}/\text{sec}\]
done
clear
D)
\[\text{1}\text{.5}\,\,\text{c}{{\text{m}}^{\text{3}}}\text{/s}\]
done
clear
View Answer play_arrow
question_answer 16) The energy of photon of wavelength \[5000\overset{\text{o}}{\mathop{\text{A}}}\,\] is nearly 2.5 eV. Then the energy of X-ray photon of wavelength 1 A will be nearly :
A)
\[3\,\,\text{c}{{\text{m}}^{\text{3}}}\text{/s}\]
done
clear
B)
\[2\,\,\text{c}{{\text{m}}^{\text{3}}}\text{/s}\]
done
clear
C)
\[{{E}_{n}}=\frac{-13.6}{{{n}^{2}}}eV\]
done
clear
D)
\[\text{91}0\text{ { }\!\!\mathrm{\AA}\!\!\text{ }},\text{ 1213 { }\!\!\mathrm{\AA}\!\!\text{ }}\]
done
clear
View Answer play_arrow
question_answer 17) The wavelength of light observed on the earth from a moving star is found to decrease by 0.05%. The star is :
A)
coming closer with a velocity of \[\text{5463}\,\overset{\text{o}}{\mathop{\text{A}}}\,,\text{ 7858}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
moving away with a velocity of \[\text{1315}\,\overset{\text{o}}{\mathop{\text{A}}}\,,\text{ 1530}\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
coming closer with a velocity of \[\text{5}.\text{67}\times \text{l}{{0}^{\text{7}}}\text{m}/\text{s}\]
done
clear
D)
moving away with a velocity of \[0.\text{95 }\times \text{ 1}{{0}^{\text{7}}}\text{ m}/\text{s}\]
done
clear
View Answer play_arrow
question_answer 18) A transistor is used as an amplifier in CB mode with a load resistance of \[\text{1}.\text{89 }\times \text{ 1}{{0}^{7}}\text{ m}/\text{s}\]. The current gain of amplifier is 0.98 and the input resistance is \[\text{3}.\text{78 }\times \text{l}{{0}^{\text{7}}}\text{ m}/\text{s}\], the voltage gain and power gain respectively are :
A)
70, 68.6
done
clear
B)
80, 75.6
done
clear
C)
60, 66.6
done
clear
D)
90, 96.6
done
clear
View Answer play_arrow
question_answer 19) A whistle of frequency 500 Hz, tied to the end of a string of length 1.2 m, revolves at 400 rev/min. A listener standing some distance away in the plane of rotation of whistle hears frequencies in the range of (speed of sound = 340 m/s):
A)
436 to 386 Hz
done
clear
B)
426 to 474 Hz
done
clear
C)
426 to 586 Hz
done
clear
D)
436 to 586 Hz
done
clear
View Answer play_arrow
question_answer 20) In LCR circuit, an alternating emf of angular frequency co is applied then the total impedance will be :
A)
\[2.5\times {{(5000)}^{2}}eV\]
done
clear
B)
\[\text{2}.\text{5 }\times \text{ 5}000\text{ eV}\]
done
clear
C)
\[\frac{2.5}{5000}eV\]
done
clear
D)
\[\frac{2.5}{{{(5000)}^{2}}}eV\]
done
clear
View Answer play_arrow
question_answer 21) In A.C. circuit a resistance of \[\text{1}.\text{5 }\times \text{ 1}{{0}^{\text{4}}}\text{ m}/\text{s}\] is connected in series with an inductance L. If the phase difference between the current and voltage is 45°, the inductive reactance will be :
A)
R/2
done
clear
B)
R/4
done
clear
C)
R
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 22) The output voltage of a transformer connected to 220 volt line is 1100 volt at 2 ampere current. Its efficiency is 100%. The current coming from the line is :
A)
20 A
done
clear
B)
10 A
done
clear
C)
11 A
done
clear
D)
22 A
done
clear
View Answer play_arrow
question_answer 23) A circular coil has 500 turns of wire and its radius is 5 cm. The self inductance of the coil is :
A)
\[\text{1}.\text{5 }\times \text{ 1}{{0}^{\text{4}}}\text{ m}/\text{s}\]
done
clear
B)
25 mH
done
clear
C)
\[\text{1}.\text{5 }\times \text{ 1}{{0}^{5}}\text{ m}/\text{s}\]
done
clear
D)
\[\text{1}.\text{5 }\times \text{ 1}{{0}^{5}}\text{ m}/\text{s}\]
done
clear
View Answer play_arrow
question_answer 24) 2m long wire is moved with a velocity 1 m/s in a magnetic field of intensity 0.5 Wb/m in direction perpendicular to the field. The emf induced in it will be .
A)
2V
done
clear
B)
\[5K\Omega \]
done
clear
C)
0.1 V
done
clear
D)
0.5 V
done
clear
View Answer play_arrow
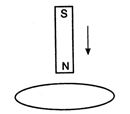
question_answer 25)
The north pole of a magnet is brought near a metallic ring as shown in the fig. The direction of induced current in the ring will be :
A)
clock wise
done
clear
B)
anti-clock wise
done
clear
C)
first clock wise then anti-clock wise
done
clear
D)
first anti-clock wise then clock wise
done
clear
View Answer play_arrow
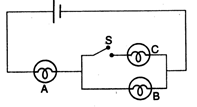
question_answer 26)
In the given fig. A, B and C are three identical bulbs. When the switch S is closed :
A)
the brightness of bulb A does not change and that of B decreases
done
clear
B)
the brightness of bulb A increases and that of B decreases
done
clear
C)
the brightness of A increases bulb B does not glow
done
clear
D)
the brightness of both bulbs A and B decrease
done
clear
View Answer play_arrow
question_answer 27) Two bulbs of 100 W and 200 W working at 220 volt are joined in series with 220 volt supply. Total power consumed will be :
A)
65 watt
done
clear
B)
33 watt
done
clear
C)
300 watt
done
clear
D)
100 watt
done
clear
View Answer play_arrow
question_answer 28) An electron (\[70\Omega \]) kg and charge \[{{\left[ {{(R\omega )}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{1/2}}\]) is moving in a circular orbit in a ^magnetic field of\[{{\left[ {{R}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{\frac{-1}{2}}}\]. Its period of revolution is :
A)
\[{{[{{R}^{2}}+{{(L\omega -C\omega )}^{2}}]}^{1/2}}\]
done
clear
B)
\[{{\left[ {{R}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{-1/2}}\]
done
clear
C)
\[R\Omega \]
done
clear
D)
\[\text{25}\times \text{1}{{0}^{-\text{3}}}\text{ mH}\]
done
clear
View Answer play_arrow
question_answer 29) 1.5 m long wire carries a current 5A. It experiences a force of 7.5 N when placed in a uniform magnetic field of intensity 2T. The angle between the magnetic field and direction of current is :
A)
\[90{}^\circ \]
done
clear
B)
\[60{}^\circ \]
done
clear
C)
\[45{}^\circ \]
done
clear
D)
\[30{}^\circ \]
done
clear
View Answer play_arrow
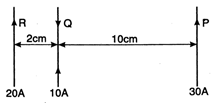
question_answer 30)
Currents flow m three long straight parallel long wires as shown in fig. The force on 10 cm length of wire Q is:
A)
\[\text{5}0\times \text{1}{{0}^{-\text{3}}}\text{H}\]N towards left
done
clear
B)
\[\text{5}0\times \text{1}{{0}^{-\text{3}}}\text{mH}\] N towards right
done
clear
C)
\[1V\]N towards right
done
clear
D)
\[\text{mass}=\text{9}.0\times \text{1}{{0}^{\text{-31}}}\] towards left
done
clear
View Answer play_arrow
question_answer 31) An ammeter gives full scale deflection when a current of 2A flows through it. The resistance of ammeter is \[1.6\times {{10}^{-19}}C\]. If the same ammeter is to be used for measusring a maximum current of 5A, then ammeter must be connected with a resistance of :
A)
\[\text{1}\text{.0}\times \text{1}{{\text{0}}^{\text{-4}}}\text{Wb}/{{\text{m}}^{\text{2}}}\] in parallel
done
clear
B)
\[\text{2}.\text{1}\times \text{1}{{0}^{-\text{6}}}\text{ s}\]. in parallel
done
clear
C)
\[\text{1}.0\text{5}\times \text{1}{{0}^{-\text{6}}}\text{ s}\]. is series
done
clear
D)
\[7\times \text{1}{{0}^{-7}}\text{ s}\]. is series
done
clear
View Answer play_arrow
question_answer 32) The emf of a primary cell is 2 volt. When it is short circuited it provides 4A current then the internal resistance of cell will be :
A)
\[3.5\times {{10}^{-7}}s\]
done
clear
B)
\[\text{2}.\text{6}\times \text{1}{{0}^{-\text{4}}}\]
done
clear
C)
\[\text{2}.\text{6}\times \text{1}{{0}^{-\text{4}}}\]
done
clear
D)
\[\text{1}.\text{4 }\times \text{1}{{0}^{-\text{4}}}\]
done
clear
View Answer play_arrow
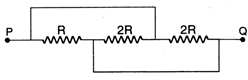
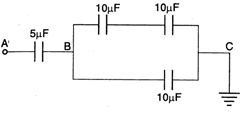
question_answer 33)
The equivalent resistance between the points P and Q in the given circuit is :
A)
\[\text{1}.\text{4 }\times \text{1}{{0}^{-\text{4}}}\]
done
clear
B)
\[12\Omega \]
done
clear
C)
2R
done
clear
D)
5R
done
clear
View Answer play_arrow
question_answer 34) The resistivity of wire depends upon :
A)
its material
done
clear
B)
its shape
done
clear
C)
its length
done
clear
D)
its area of cross-section
done
clear
View Answer play_arrow
question_answer 35) A rod of certain metal is 1.0 m long and 0.6 cm in diameter and its resistance is \[18\Omega \]Another disc made of same metal is 2.0 cm in dimeter and 1.0 mm long. The resistance between the round faces of the disc is :
A)
\[8\Omega \].
done
clear
B)
\[18\Omega \]
done
clear
C)
\[8\Omega \]
done
clear
D)
\[8\Omega \]
done
clear
View Answer play_arrow
question_answer 36) A \[2.0\Omega \]capacitor is charged to 100 V and then its plates are connected by a conducting wire. The heat produced is :
A)
\[4\Omega \]
done
clear
B)
\[0.5\Omega \]
done
clear
C)
\[\frac{6R}{5}\]
done
clear
D)
\[\frac{R}{2}\]
done
clear
View Answer play_arrow
question_answer 37) An \[3\times {{10}^{-3}}\Omega \] particle is accelerated through a p.d of 106 volt then K.E. of particle will be:
A)
8 MeV
done
clear
B)
4 MeV
done
clear
C)
2 MeV
done
clear
D)
1 MeV
done
clear
View Answer play_arrow
question_answer 38)
As shown m fig if the point C is earthed and the point A is given a potential of 2000 volt then the potential at point B will be :
A)
400 V
done
clear
B)
500 V
done
clear
C)
1000 V
done
clear
D)
1300 V
done
clear
View Answer play_arrow
question_answer 39) The radius of nucleus of silver (atomic number = 47) is\[\text{8}.\text{1}0\times \text{1}{{0}^{-\text{5}}}\text{ }\Omega \]. The electric potential on the surface of nucleus is : \[\text{4}.0\text{5}\times \text{1}{{0}^{-\text{6}}}\text{ }\Omega \]
A)
\[\text{1}\text{.35}\times \text{1}{{0}^{-8}}\text{ }\Omega \]
done
clear
B)
\[2.70\times \text{1}{{0}^{-7}}\Omega \]
done
clear
C)
\[2\mu F\]
done
clear
D)
\[0.00\text{1 J}\]
done
clear
View Answer play_arrow
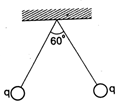
question_answer 40)
Two small sphere balls each carrying charge \[0.0\text{1 J}\] are suspended by two insulated threads of equal length 1 m each, from a point fixed in the ceiling. It is found that in equilibrium, threads are separated by an angle 60° between them as shown in fig., the tension in the thread is :
A)
0.18 N
done
clear
B)
18 N
done
clear
C)
1.8 N
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 41) At a certain place the horizontal component of the earths magnetic field is \[\text{15 J}\] and the angle of dip is \[45{}^\circ \] then total intensity of field at that place will be :
A)
\[0.\text{1 J}\]
done
clear
B)
\[\alpha \]
done
clear
C)
\[\text{3}.\text{4}\times \text{1}{{0}^{-\text{14}}}\text{ m}\]
done
clear
D)
\[(e=1.6\times {{10}^{-19}}C)\]
done
clear
View Answer play_arrow
question_answer 42) A diver inside water (\[\text{1}.\text{99}\times \text{1}{{0}^{\text{6}}}\text{volt}\]) should see the sun set at an angle of :
A)
\[60{}^\circ \]
done
clear
B)
\[90{}^\circ \]
done
clear
C)
\[0{}^\circ \]
done
clear
D)
\[49{}^\circ \]
done
clear
View Answer play_arrow
question_answer 43) The mean distance of sun from the earth is \[\text{2}.\text{9}\times \text{1}{{0}^{\text{6}}}\text{volt}\](nearly). The time taken by the light to reach earth from the sun is :
A)
0.12 min
done
clear
B)
8.33 min
done
clear
C)
12.5 min
done
clear
D)
6.25 min
done
clear
View Answer play_arrow
question_answer 44) A monochromatic light ray of frequency\[\text{4}.\text{99}\times \text{1}{{0}^{\text{6}}}\text{volt}\]from vacuum enters in a medium of refractive index 1.5. Its wavelength in medium will be :
A)
\[5500\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
B)
\[6000\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
C)
\[5000\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
D)
\[4000\overset{\text{o}}{\mathop{\text{A}}}\,\]
done
clear
View Answer play_arrow
question_answer 45) The spectrum of red hot heater will be :
A)
continuous
done
clear
B)
band
done
clear
C)
line
done
clear
D)
absorption
done
clear
View Answer play_arrow
question_answer 46) The focal lengths of convex lens for red and blue light are 100 cm and 96.8 cm respectively. The dispersive power of material of lens is :
A)
0.325
done
clear
B)
0.0325
done
clear
C)
0.98
done
clear
D)
0.968
done
clear
View Answer play_arrow
question_answer 47) The power of an achromatic convergent lens of two lenses is + 2D. The power of convex lens is +5D. The ratio of dispersive power of convex and concave lenses will be :
A)
5 : 3
done
clear
B)
3:5
done
clear
C)
2:5
done
clear
D)
5 : 2
done
clear
View Answer play_arrow
question_answer 48) The diameter of objective of a telescope is 1m. Its resolving limit for the light of wavelength \[4538\overset{\text{o}}{\mathop{\text{A}}}\,\], will be :
A)
\[2B_{0}^{{}}\]
done
clear
B)
\[\sqrt{2}B_{0}^{{}}\]
done
clear
C)
\[B_{0}^{{}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 49) A man cannot see distinctly an object beyond 5m. He wants to see the stars. The focal length of the lens which he must use, will be :
A)
12.5 m
done
clear
B)
65 m
done
clear
C)
6 m
done
clear
D)
5 m
done
clear
View Answer play_arrow
question_answer 50) For thorium A = 232, Z = 90 at the end of some radioactive disintegration we obtain an isotope of lead with A = 208 and Z = 82, then the number of emitted a and P particles are :
A)
\[\mu =\text{1}.\text{33}\]
done
clear
B)
\[\text{1}.\text{5}\times \text{1}{{0}^{\text{8}}}\text{ km}\]
done
clear
C)
\[\text{5}\times \text{1}0{{~}^{14}}\text{Hz}\]
done
clear
D)
\[\text{55}00\text{ { }\!\!\mathrm{\AA}\!\!\text{ }}\]
done
clear
View Answer play_arrow
question_answer 51) The k line of singly ionised calcium has a wavelength of 393.3 nm as measured on earth. In the spectrum of one of the observed galaxies, this spectral line is located at 401.8 nm. The speed with which the galaxy is moving away from us, will be :
A)
6480 km/s
done
clear
B)
3240 km/s
done
clear
C)
4240 km/s
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 52) If unit of length, mass and time each be doubled, the unit of work done is increased by
A)
4 times
done
clear
B)
6 times
done
clear
C)
8 times
done
clear
D)
2 times
done
clear
View Answer play_arrow
question_answer 53) The dimensional formula of universal gas constant:
A)
\[\text{6}000\text{ { }\!\!\mathrm{\AA}\!\!\text{ }}\]
done
clear
B)
\[\text{5}000\text{ { }\!\!\mathrm{\AA}\!\!\text{ }}\]
done
clear
C)
\[\text{4000 { }\!\!\mathrm{\AA}\!\!\text{ }}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 54) A geostationary satellite is orbiting the earth at the height of 6R above the surface of earth, R being radius of earth. The time period of another satellite at a height of 2.5 R from the surface of earth, is:
A)
10 hour
done
clear
B)
\[\text{5}.\text{54}\times \text{1}{{0}^{-\text{7}}}\text{rad}\] hour
done
clear
C)
6 hour
done
clear
D)
\[\text{2}.\text{54}\times \text{1}{{0}^{-\text{4}}}\text{ rad}\] hour
done
clear
View Answer play_arrow
question_answer 55) 5 g of ice at \[0{}^\circ C\] is dropped in a beaker containing 20 g of water at \[40{}^\circ C\]. The final temperature will be:
A)
\[32{}^\circ C\]
done
clear
B)
\[16{}^\circ C\]
done
clear
C)
\[8{}^\circ C\]
done
clear
D)
\[24{}^\circ C\]
done
clear
View Answer play_arrow
question_answer 56) Beryllium shows diagonal relationship with :
A)
Mg
done
clear
B)
Na
done
clear
C)
B
done
clear
D)
Al
done
clear
View Answer play_arrow
question_answer 57) For a reaction, the rate constant is\[\text{6}.\text{54}\times \text{1}{{0}^{-\text{7}}}\text{rad}\]. The half-life period for the inaction is :
A)
0.30 sec
done
clear
B)
0.60 sec
done
clear
C)
3.3 sec
done
clear
D)
data is insufficient
done
clear
View Answer play_arrow
question_answer 58) Artificial radioactivity was discovered by:
A)
Pault
done
clear
B)
Rutherford
done
clear
C)
Soddy
done
clear
D)
Curie
done
clear
View Answer play_arrow
question_answer 59) Electrolysis of an aqueous solution of sodium acetate, yields :
A)
ethane
done
clear
B)
ethane
done
clear
C)
ethane
done
clear
D)
propane
done
clear
View Answer play_arrow
question_answer 60) Ethyl acetoacetate shows, which type of isomerism?
A)
Chain
done
clear
B)
Optical
done
clear
C)
Metamerism
done
clear
D)
Tautomerism
done
clear
View Answer play_arrow
question_answer 61) Which of the following gas is insoluble in water?
A)
\[\alpha =\text{4},\beta =\text{6}~~~~\]
done
clear
B)
\[\alpha =\text{5},\beta =\text{5}\]
done
clear
C)
\[\alpha =\text{6},\beta =\text{4}\]
done
clear
D)
\[\alpha =\text{6},\beta =\text{6}\]
done
clear
View Answer play_arrow
question_answer 62) Dual nature of particles was proposed by:
A)
Heisenberg
done
clear
B)
Lowry
done
clear
C)
De-Broglie
done
clear
D)
Schrodinger
done
clear
View Answer play_arrow
question_answer 63) sp hybridisation is found in :
A)
\[[M{{L}^{2}}{{T}^{-2}}{{\theta }^{-1}}]\]
done
clear
B)
\[[{{M}^{2}}L{{T}^{-2}}\theta ]\]
done
clear
C)
\[[M{{L}^{3}}{{T}^{-1}}{{\theta }^{-1}}]\]
done
clear
D)
\[\frac{6}{\sqrt{2}}\]
done
clear
View Answer play_arrow
question_answer 64) Which of the following is an ore of lead?
A)
Galena
done
clear
B)
Calamine
done
clear
C)
Malachite
done
clear
D)
Dolomite
done
clear
View Answer play_arrow
question_answer 65) The compound X, in the reaction, is :\[6\sqrt{2}\]\[\text{2}.\text{34 se}{{\text{c}}^{\text{-1}}}\]
A)
\[\text{S}{{\text{O}}_{\text{2}}}\]
done
clear
B)
\[\text{N}{{\text{H}}_{3}}\]
done
clear
C)
\[{{\text{H}}_{\text{2}}}\]
done
clear
D)
\[\text{C}{{\text{O}}_{\text{2}}}\]
done
clear
View Answer play_arrow
question_answer 66) Which of the following compound give yellow precipitate with l2 and NaOH?
A)
\[\text{CO}_{3}^{2-}\]
done
clear
B)
\[B{{F}_{3}}\]
done
clear
C)
\[\text{NO}_{3}^{-}\]
done
clear
D)
\[N{{H}_{3}}\]
done
clear
View Answer play_arrow
question_answer 67) The laws of electrolysis were proposed by:
A)
Kohlraush
done
clear
B)
Faraday
done
clear
C)
Nernst
done
clear
D)
Berthelot
done
clear
View Answer play_arrow
question_answer 68) Which of the following does not react with \[X\xrightarrow{C{{H}_{3}}Mgl}Y\xrightarrow{hydrolysis}Mg(OH)I\]?
A)
\[C{{H}_{3}}COOH:\]
done
clear
B)
\[C{{H}_{3}}CHO\]
done
clear
C)
HCHO
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 69) What is the product in the reaction, \[C{{H}_{3}}CON{{H}_{2}}\xrightarrow[{}]{NaN{{O}_{2}}HCl}X\]
A)
\[{{(C{{H}_{3}})}_{2}}CO\]
done
clear
B)
\[HCHO\]
done
clear
C)
\[\text{C}{{\text{H}}_{\text{3}}}\text{OH}\]
done
clear
D)
\[\text{C}{{\text{H}}_{\text{3}}}\text{C}{{\text{H}}_{\text{2}}}\text{C}{{\text{H}}_{\text{2}}}\text{OH}\]
done
clear
View Answer play_arrow
question_answer 70) Which of the following .is not a Lewis base?
A)
\[{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{O}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\]
done
clear
B)
\[\text{C}{{\text{H}}_{\text{3}}}\text{C}{{\text{H}}_{\text{2}}}\text{OH}\]
done
clear
C)
\[\text{NaHS}{{\text{O}}_{\text{3}}}\]
done
clear
D)
\[\text{C}{{\text{H}}_{\text{3}}}\text{COC}{{\text{H}}_{\text{3}}}\]
done
clear
View Answer play_arrow
question_answer 71) The unit of molality is :
A)
mole per litre
done
clear
B)
mole per kilogram
done
clear
C)
per mole per litre
done
clear
D)
mole litre
done
clear
View Answer play_arrow
question_answer 72) What is the ratio of diffusion rate of oxygen and hydrogen?
A)
1:4
done
clear
B)
4:1
done
clear
C)
1 : 8
done
clear
D)
8 : 1
done
clear
View Answer play_arrow
question_answer 73) For the gaseous reaction,\[\text{C}{{\text{H}}_{\text{3}}}\text{CHO}\]
A)
\[\text{C}{{\text{H}}_{\text{3}}}\text{CON}{{\text{H}}_{2}}\xrightarrow{NaN{{O}_{2}}/HCl}X\]
done
clear
B)
\[\text{C}{{\text{H}}_{\text{3}}}\text{COOH}\]
done
clear
C)
\[\overset{+}{\mathop{\text{C}{{\text{H}}_{\text{3}}}\text{CON}{{\text{H}}_{\text{3}}}{{\text{C}}^{-}}}}\,\]
done
clear
D)
\[\text{C}{{\text{H}}_{\text{3}}}\text{N}{{\text{H}}_{\text{2}}}\]
done
clear
View Answer play_arrow
question_answer 74) The oxidation number of Fe in\[\text{C}{{\text{H}}_{\text{3}}}\text{CHO}\]is :
A)
+3
done
clear
B)
+4
done
clear
C)
+2
done
clear
D)
-2
done
clear
View Answer play_arrow
question_answer 75) Which enzyme convert glucose into alcohol?
A)
Invertase
done
clear
B)
Zymase
done
clear
C)
Maltase
done
clear
D)
Diastase
done
clear
View Answer play_arrow
question_answer 76) Fehling solution is :
A)
\[{{\text{H}}_{\text{2}}}\text{O}\]lime
done
clear
B)
\[\text{A}{{\text{g}}^{+}}\]
done
clear
C)
\[\text{N}{{\text{H}}_{\text{3}}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 77) Glucose reacts with bromine water to produce :
A)
gluconic acid
done
clear
B)
glyceraldehyde
done
clear
C)
saccharic acid
done
clear
D)
glucaric acid
done
clear
View Answer play_arrow
question_answer 78) \[O{{H}^{-}}\], product X is :
A)
ethylene bromide
done
clear
B)
vinyl bromide
done
clear
C)
bromo ethane
done
clear
D)
ethyledine bromide
done
clear
View Answer play_arrow
question_answer 79) Glycerol reacts with potassium bisulphate to produce :
A)
allyl iodide
done
clear
B)
allyl sulphate
done
clear
C)
acryl aldehyde
done
clear
D)
glycerol trisulphate
done
clear
View Answer play_arrow
question_answer 80) Sorels cement is :
A)
Portland cement + MgO
done
clear
B)
\[{{N}_{2}}{{O}_{4}}\xrightarrow{{}}2N{{O}_{2}}\]
done
clear
C)
\[\Delta H<\Delta E\]
done
clear
D)
\[\Delta H=\Delta E\]
done
clear
View Answer play_arrow
question_answer 81) Which of the following is the strongest acid?
A)
\[\Delta H=0\]
done
clear
B)
\[\Delta H>\Delta E\]
done
clear
C)
\[{{\text{K}}_{\text{4}}}\left[ \text{Fe}{{\left( \text{CN} \right)}_{\text{6}}} \right]\]
done
clear
D)
\[\text{CuS}{{\text{O}}_{\text{4}}}\text{+}\]
done
clear
View Answer play_arrow
question_answer 82) Which law of thermodynamics help in calculating entropy at different temperatures?
A)
First law
done
clear
B)
Second law
done
clear
C)
Third law
done
clear
D)
Zeroth law
done
clear
View Answer play_arrow
question_answer 83) At NTP, the density of a gas, whose molecular weight is 45, is :
A)
44.8 gm/litre
done
clear
B)
11.4 gm/litre
done
clear
C)
2 gm /litre
done
clear
D)
3 gm/litre
done
clear
View Answer play_arrow
question_answer 84) At equilibrium, the Gibbs free energy is :
A)
+ ve
done
clear
B)
- ve
done
clear
C)
zero
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 85) Which of the following is not an organometallic compound?
A)
Zeisses salt
done
clear
B)
TEL
done
clear
C)
Sodium ethoxide
done
clear
D)
Ferrocene
done
clear
View Answer play_arrow
question_answer 86) Which of the following ions, will have maximum hydration energy?
A)
\[\text{CuS}{{\text{O}}_{\text{4}}}\text{+NaOH(aq)}\]
done
clear
B)
\[\text{CuS}{{\text{O}}_{\text{4}}}+\text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}\]
done
clear
C)
\[CH\equiv CH+HBr\to X\]
done
clear
D)
\[\text{MgC}{{l}_{\text{2}}}.\text{CaSi}{{\text{O}}_{\text{3}}}.\text{2}{{\text{H}}_{\text{2}}}\text{O}\]
done
clear
View Answer play_arrow
question_answer 87) Which set of hydridisation is correct for the following compounds? \[\text{CaSi}{{\text{O}}_{\text{3}}}.\text{MgC}{{\text{O}}_{\text{3}}}\] \[\text{MgC}{{l}_{\text{2}}}.\text{5MgO}.;x{{H}_{\text{2}}}O\] \[HCl{{O}_{4}}\]
A)
sp, \[HCl{{O}_{3}}\], \[HCl{{O}_{2}}\]
done
clear
B)
sp, \[HClO\], \[S{{r}^{2+}}\]
done
clear
C)
\[B{{a}^{2+}}\] \[C{{a}^{2+}}\] \[M{{g}^{2+}}\]
done
clear
D)
\[\text{N}{{\text{O}}_{\text{2}}}\] \[~\text{S}{{\text{F}}_{\text{4}}}\] \[\text{P}{{\text{F}}_{\text{6}}}\]
done
clear
View Answer play_arrow
question_answer 88) Phenol is more acidic than :
A)
done
clear
B)
done
clear
C)
\[~\text{s}{{\text{p}}^{\text{2}}}\]
done
clear
D)
both (a) and (c)
done
clear
View Answer play_arrow
question_answer 89) The reaction, \[\text{s}{{\text{p}}^{\text{3}}}\]Product, is called :
A)
Perkin reaction
done
clear
B)
Levit reaction
done
clear
C)
Wurtz reaction
done
clear
D)
Aldol condensation
done
clear
View Answer play_arrow
question_answer 90) PVC is prepared by the polymerization of:
A)
ethylene
done
clear
B)
1-chloropopene
done
clear
C)
propene
done
clear
D)
1-chloroethene
done
clear
View Answer play_arrow
question_answer 91) \[\text{s}{{\text{p}}^{\text{3}}}\text{d}\] The product B is :
A)
malonic acid
done
clear
B)
glycolic acid
done
clear
C)
lactic acid
done
clear
D)
malic acid
done
clear
View Answer play_arrow
question_answer 92) Solder is an alloy of :
A)
\[\text{s}{{\text{p}}^{\text{3}}}{{\text{d}}^{\text{2}}}\]
done
clear
B)
\[\text{s}{{\text{p}}^{\text{2}}},\]
done
clear
C)
\[\text{s}{{\text{p}}^{3}},\]
done
clear
D)
\[{{\text{d}}^{2}}\text{s}{{\text{p}}^{3}}\]
done
clear
View Answer play_arrow
question_answer 93) The maximum number of electrons in \[\text{s}{{\text{p}}^{3}},\]-orbital with n = 5, m = 1 is :
A)
6
done
clear
B)
2
done
clear
C)
14
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 94) Wolf Kishner reduction, reduces :
A)
-COOH group
done
clear
B)
-C= C- group
done
clear
C)
-CHO group
done
clear
D)
-0- group
done
clear
View Answer play_arrow
question_answer 95) The solubility product of \[\text{s}{{\text{p}}^{3}}{{d}^{2}},\]is\[\text{s}{{\text{p}}^{3}}{{d}^{2}}\]. What is the solubility of \[{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}\]?
A)
\[C{{H}_{3}}Br+Na\to \]
done
clear
B)
\[C{{H}_{3}}CHO\xrightarrow{HCN}A\xrightarrow{HOH}B\]
done
clear
C)
\[\text{Pb}+\text{Zn}+\text{Sn}\]
done
clear
D)
\[\text{Pb}+\text{Zn}\]
done
clear
View Answer play_arrow
question_answer 96) For reaction, \[\text{Pb}+\text{Sn}\], the value of kc will be equal to :
A)
\[\text{Sn}+\text{Zn}\]
done
clear
B)
\[p\]
done
clear
C)
\[\text{A}{{\text{s}}_{\text{2}}}{{\text{S}}_{\text{3}}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 97) Molecular orbital theory was proposed by:
A)
Gillespie and Nyholm
done
clear
B)
Pauling
done
clear
C)
Slater
done
clear
D)
Hund and Mulliken
done
clear
View Answer play_arrow
question_answer 98) The correct order of basicity of amines in water is :
A)
\[\text{2}.\text{8}\times \text{l}{{\text{0}}^{\text{-72}}}\]
done
clear
B)
\[\text{A}{{\text{s}}_{\text{2}}}{{\text{S}}_{\text{3}}}\]
done
clear
C)
\[\text{1}.\text{92 }\times \text{1}{{\text{0}}^{\text{-15}}}\text{ mole}/\text{litre}\]
done
clear
D)
\[\text{1}.7\text{2 }\times \text{1}{{\text{0}}^{\text{-15}}}\text{ mole}/\text{litre}\]
done
clear
View Answer play_arrow
question_answer 99) A galvanic cell with electrode potential of A=+2.23V and B= 1.43V. The value of E°cell is :
A)
3.66 V
done
clear
B)
0.80 V
done
clear
C)
-0.80 V
done
clear
D)
-3.66 V
done
clear
View Answer play_arrow
question_answer 100) A non ideal solution was prepared by mixing 30 ml chloroform and 50 ml acetone. The volume of mixture will be :
A)
>80 ml
done
clear
B)
< 80 ml
done
clear
C)
= 80 ml
done
clear
D)
\[\text{2}.\text{3 }\times \text{1}{{0}^{-\text{16}}}\text{ mole}/\text{litre}\]
done
clear
View Answer play_arrow
question_answer 101) The half-life of \[\text{1}.\text{65}\times \text{1}{{0}^{-\text{36}}}\text{ mole}/\text{litre}\] is (disintegration constant,\[2A(g)3C(g)+D(s)\]) :
A)
\[{{K}_{p}}(RT)\]
done
clear
B)
\[{{K}_{p}}/RT\]
done
clear
C)
\[={{K}_{p}}\]
done
clear
D)
\[{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{2}}}\text{NH}>{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{3}}}\text{N}>\text{C}{{\text{H}}_{\text{3}}}\text{N}{{\text{H}}_{\text{2}}}\]
done
clear
View Answer play_arrow
question_answer 102) Which of the following is a protein?
A)
Pepsin
done
clear
B)
Adrenaline
done
clear
C)
ATP
done
clear
D)
Glutamin
done
clear
View Answer play_arrow
question_answer 103) Which of the following is a mixed oxide?
A)
\[\text{C}{{\text{H}}_{\text{3}}}\text{N}{{\text{H}}_{\text{2}}}>{{(\text{C}{{\text{H}}_{\text{3}}}\text{)}}_{2}}\text{NH}>{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{3}}}\text{N}\]
done
clear
B)
\[{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{3}}}\text{N}>{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{2}}}\text{NH}>\text{C}{{\text{H}}_{\text{3}}}\text{N}{{\text{H}}_{\text{2}}}\]
done
clear
C)
\[{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{3}}}\text{N}>\text{C}{{\text{H}}_{\text{3}}}\text{N}{{\text{H}}_{\text{2}}}>{{\left( \text{C}{{\text{H}}_{\text{3}}} \right)}_{\text{2}}}\text{NH}\]
done
clear
D)
\[\ge \text{8}0\text{ ml}\]
done
clear
View Answer play_arrow
question_answer 104) Which of the following has diamagnetic character?
A)
\[_{6}{{C}^{14}}\]
done
clear
B)
\[\lambda =\text{2}.\text{31}\times \text{1}{{0}^{-\text{4}}}\text{ yea}{{\text{r}}^{\text{-1}}}\]
done
clear
C)
\[\text{4}\times \text{1}{{0}^{\text{2}}}\text{ years}\]
done
clear
D)
\[\text{3}.\text{5}\times \text{1}{{0}^{\text{4}}}\text{ years}\]
done
clear
View Answer play_arrow
question_answer 105) An anaesthetic is :
A)
procaine
done
clear
B)
chloramphenicol
done
clear
C)
\[\text{2}\times \text{1}{{0}^{\text{2}}}\text{ years}\]-hexyl resorcinol
done
clear
D)
cibazol
done
clear
View Answer play_arrow
question_answer 106) Ozone with dry iodine give :
A)
\[\text{3}\times \text{1}{{0}^{\text{3}}}\text{years}\]
done
clear
B)
\[\text{F}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}\]
done
clear
C)
\[\text{Pb}{{\text{O}}_{\text{2}}}\]
done
clear
D)
\[\text{P}{{\text{b}}_{\text{3}}}{{\text{O}}_{\text{4}}}\]
done
clear
View Answer play_arrow
question_answer 107) 2.76 g of silver carbonate on being strongly heated yield a residue weighing:
A)
2.16 g
done
clear
B)
2.48 g
done
clear
C)
2.64 g
done
clear
D)
2.32 g
done
clear
View Answer play_arrow
question_answer 108) Which of the following properties show gradual decrease with increase in atomic number across a period in the periodic table?
A)
Electron affinity
done
clear
B)
lonization potential
done
clear
C)
Electronegativity
done
clear
D)
Size of atom
done
clear
View Answer play_arrow
question_answer 109) When KBr is treated with concentrated \[\text{Ba}{{\text{O}}_{\text{2}}}\]redish brown gas evolved, gas is :
A)
mixture of bromine and HBr
done
clear
B)
\[{{[NiC{{l}_{4}}]}^{2-}}\]
done
clear
C)
bromine
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 110) Which of the following basic radicals will not be precipitated by H2S gas in the presence of\[{{[CO{{F}_{6}}]}^{3-}}\]?
A)
\[{{[Fe{{({{H}_{2}}O)}_{6}}]}^{2+}}\]
done
clear
B)
\[{{[Ni{{(CN)}_{4}}]}^{2-}}\]
done
clear
C)
\[n\]
done
clear
D)
\[{{I}_{4}}{{O}_{4}}\]
done
clear
View Answer play_arrow
question_answer 111) \[{{I}_{2}}{{O}_{3}}\] is equal to:
A)
\[I{{O}_{2}}\]
done
clear
B)
\[{{I}_{2}}{{O}_{4}}\]
done
clear
C)
\[{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\]
done
clear
D)
\[\text{HBr}\]
done
clear
View Answer play_arrow
question_answer 112) \[\text{N}{{\text{H}}_{\text{3}}}\]will be purely imaginary, if \[M{{n}^{2+}}\] is equal to :
A)
\[N{{i}^{2+}}\]
done
clear
B)
\[C{{d}^{2+}}\]
done
clear
C)
\[C{{a}^{2+}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 113) If three complex number are in A.R, then they lie on :
A)
a circle in the complex plane
done
clear
B)
a straight line in the complex plane
done
clear
C)
a parabola in the complex plane
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 114) If the cube roots of unity are \[\left( \frac{1}{1-2i}+\frac{3}{1+i} \right)\left( \frac{3+4i}{2-4i} \right)\] then the roots of the equation\[\frac{1}{2}+\frac{9}{2}i\] are :
A)
\[\frac{1}{2}-\frac{9}{2}i\]
done
clear
B)
\[\frac{1}{4}-\frac{9}{4}i\]
done
clear
C)
\[\frac{1}{4}+\frac{9}{4}i\]
done
clear
D)
\[\frac{3+2i\sin \theta }{1-2i\sin \theta }\]
done
clear
View Answer play_arrow
question_answer 115) 99th term of the series\[\theta \]is :
A)
9998
done
clear
B)
9999
done
clear
C)
10000
done
clear
D)
100000
done
clear
View Answer play_arrow
question_answer 116) If a, b, c, d and p are different real numbers such that\[2n\pi \pm \frac{\pi }{3}\]\[n\pi +\frac{\pi }{3}\], then a, b, c, d are in :
A)
A.P.
done
clear
B)
G.P.
done
clear
C)
H.P.
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 117) The sum of the series \[n\pi \pm \frac{\pi }{3}\] upto 20 terms is :
A)
188090
done
clear
B)
189080
done
clear
C)
199080
done
clear
D)
199089
done
clear
View Answer play_arrow
question_answer 118) \[1,\omega ,{{\omega }^{2}}\]equals :
A)
\[{{(x-2)}^{3}}+27=0\]
done
clear
B)
\[-1,-1,-1\]
done
clear
C)
\[-1,-\omega ,-{{\omega }^{2}}\]
done
clear
D)
\[-1,2+3\omega ,2+3{{\omega }^{2}}\]
done
clear
View Answer play_arrow
question_answer 119) If \[-1,2-3\omega ,2-3{{\omega }^{2}}\]and \[\text{2}+\text{7}+\text{14}+\text{23}+\text{34}...\] where \[\left( {{\text{a}}^{\text{2}}}+{{\text{b}}^{\text{2}}}+{{\text{c}}^{\text{2}}} \right){{P}^{\text{2}}}-\text{ 2}\left( \text{ab}+\text{bc}+\text{cd} \right)P\] then\[+({{b}^{2}}+{{c}^{2}}+{{d}^{2}}\le 0\] has at least :
A)
four real roots
done
clear
B)
two real roots
done
clear
C)
four imaginary roots
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 120) The solution set of the equation \[{{1.3}^{2}}+{{2.5}^{2}}+{{3.7}^{2}}+.....\] is :
A)
\[\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{n(n+1)}\]
done
clear
B)
(4)
done
clear
C)
\[\frac{1}{n(n+1)}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 121) Number of roots of the equation\[\frac{n}{(n+1)}\]is
A)
one
done
clear
B)
two
done
clear
C)
infinite
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 122) If \[\frac{2n}{(n+1)}\]and \[\frac{2}{n(n+1)}\], then the value of r is :
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 123) A student is allowed to select at most n books from a collection of \[p(x)=a{{x}^{2}}+bx+c\] books. If the total number of ways in which he can select one book is 63, then the value of n is equal to :
A)
2
done
clear
B)
3
done
clear
C)
4
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 124) The number of ways in which a committee can be formed of 5 members from 6 men and 4 women if the committee has at least one woman, is :
A)
186
done
clear
B)
246
done
clear
C)
252
done
clear
D)
244
done
clear
View Answer play_arrow
question_answer 125) \[Q(x)=-a{{x}^{2}}+dx+c\]is equal to :
A)
\[ac\ne 0\]
done
clear
B)
\[p(x).Q(x)=0\]
done
clear
C)
\[{{x}^{\log x{{(1-x)}^{2}}=9}}\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 126) The coefficient of \[(-\text{2},\text{4)}\] in the expansion of \[(0,-\text{2},\text{ 4)}\]will be :
A)
\[x-\frac{2}{x-1}=1-\frac{2}{x-1}\]
done
clear
B)
\[^{n}{{C}_{r-1}}=36{{,}^{n}}{{C}_{r}}=84\]
done
clear
C)
\[^{n}{{C}_{r-1}}=126\]
done
clear
D)
\[(2n+1)\]
done
clear
View Answer play_arrow
question_answer 127) Let n be an odd integer. If \[\sum\limits_{r=0}^{n}{^{n+r}{{C}_{n}}}\]for every value of \[^{n+m+1}{{C}_{n+1}}\],then:
A)
\[^{n+m+2}{{C}_{n}}\]
done
clear
B)
\[^{n+m+3}{{C}_{n-1}}\]
done
clear
C)
\[{{x}^{-7}}\]
done
clear
D)
\[{{\left[ ax-\frac{1}{b{{x}^{2}}} \right]}^{11}}\]
done
clear
View Answer play_arrow
question_answer 128) \[\frac{462{{a}^{6}}}{{{b}^{5}}}\]is equal to :
A)
\[\frac{462{{a}^{5}}}{{{b}^{6}}}\]
done
clear
B)
\[-\frac{462{{a}^{5}}}{{{b}^{6}}}\]
done
clear
C)
\[-\frac{462{{a}^{6}}}{{{b}^{5}}}\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 129) If k is a scalar and J is a unit matrix of order 3, then adj (kl) is equal to :
A)
\[\sin n\theta =\sum\limits_{r=0}^{n}{{{b}_{r}}{{\sin }^{r}}\theta }\]
done
clear
B)
\[\theta \]
done
clear
C)
\[{{b}_{0}}=0,{{b}_{1}}=3\]
done
clear
D)
\[{{b}_{0}}=1,{{b}_{1}}=n\]
done
clear
View Answer play_arrow
question_answer 130) The value of the determinant\[{{b}_{0}}=-1,{{b}_{1}}=n\]is equal to :
A)
\[{{b}_{0}}=0,{{b}_{1}}={{n}^{2}}-3n+3\]
done
clear
B)
\[\left| \begin{matrix} a+b & a+2b & a+3b \\ a+2b & a+3b & a+4b \\ a+4b & a+5b & a+6b \\ \end{matrix} \right|\]
done
clear
C)
\[{{a}^{2}}+{{b}^{2}}+{{c}^{2}}-3abc\]
done
clear
D)
\[3ab\]
done
clear
View Answer play_arrow
question_answer 131) If \[3a+5b\], then \[{{k}^{3}}I\] is equal to :
A)
\[{{k}^{2}}I\]
done
clear
B)
\[-{{k}^{3}}I\]
done
clear
C)
\[-{{k}^{2}}I\]
done
clear
D)
\[\left| \begin{matrix} 1 & 1 & 1 \\ 1 & 1-x & 1 \\ 1 & 1 & 1+y \\ \end{matrix} \right|\]
done
clear
View Answer play_arrow
question_answer 132) If \[3-x+y\], then \[(1-x)(1-y)\] is equal to :
A)
\[xy\]
done
clear
B)
\[-xy\]
done
clear
C)
\[A=\left[ \begin{matrix} 3 & 2 \\ 0 & 1 \\ \end{matrix} \right]\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 133) If \[{{({{A}^{-1}})}^{3}}\],then the value of \[\frac{1}{27}\left( \begin{matrix} 1 & -8 \\ 0 & 27 \\ \end{matrix} \right)\] is equal to :
A)
1
done
clear
B)
2
done
clear
C)
0
done
clear
D)
\[\frac{1}{27}\left( \begin{matrix} -1 & 26 \\ 0 & 27 \\ \end{matrix} \right)\]
done
clear
View Answer play_arrow
question_answer 134) In a \[\frac{1}{27}\left( \begin{matrix} 1 & -26 \\ 0 & -27 \\ \end{matrix} \right)\], if\[\frac{1}{27}\left( \begin{matrix} -1 & -26 \\ 0 & -27 \\ \end{matrix} \right)\], then the value of\[\alpha +\beta -\lambda =\pi \]is equal to :
A)
1
done
clear
B)
2
done
clear
C)
\[{{\sin }^{2}}\alpha +{{\sin }^{2}}\beta -{{\sin }^{2}}\gamma \]
done
clear
D)
\[\text{2 sin }\alpha \text{ sin}\beta \text{ cos }\gamma \]
done
clear
View Answer play_arrow
question_answer 135) There exist a triangle ABC, satisfying the conditions :
A)
\[\text{2 cos}\alpha \text{ cos}\beta \text{ cos }\gamma \]
done
clear
B)
\[\text{2sin}\alpha \text{ sin}\beta \text{ sin }\gamma \]
done
clear
C)
\[x\cos \theta =y\cos \left( \theta +\frac{2\pi }{3} \right)=z\cos \left( \theta +\frac{4\pi }{3} \right)\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 136) The number of values of x in the interval \[\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\] satisfying the equation \[3\,\,\,\cos \,\,\,\theta \]is :
A)
0
done
clear
B)
5
done
clear
C)
6
done
clear
D)
10
done
clear
View Answer play_arrow
question_answer 137) The angle of depression of a ship from the top of a tower 30 m high is 60°. Then the distance of ship from the base of tower is :
A)
30 m
done
clear
B)
\[\Delta ABC\]
done
clear
C)
\[\text{3a}=\text{b}+\text{c}\]
done
clear
D)
10 m
done
clear
View Answer play_arrow
question_answer 138) The area of triangle formed by the points \[\cot \frac{B}{2}\cot \frac{C}{2}\]is equal to :
A)
\[\sqrt{3}\]
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
\[b\sin A=a,A<\frac{\pi }{2}\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 139) The points (1,3) and (5,1) are the opposite vertices of a rectangle. The other two vertices lie on the line \[b\sin A>a,A>\frac{\pi }{2}\], then the value of c will be :
A)
4
done
clear
B)
-4
done
clear
C)
2
done
clear
D)
-2
done
clear
View Answer play_arrow
question_answer 140) Given the four lines with equations \[b\sin A>a,A<\frac{\pi }{2}\]and \[[0,5\pi ]\], then these lines are :
A)
concurrent
done
clear
B)
perpendicular
done
clear
C)
the sides of a rectangle
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 141) The angle between the lines \[3{{\sin }^{2}}x-7\sin x+2=0\] is equal to :
A)
45°
done
clear
B)
60°
done
clear
C)
90°
done
clear
D)
180°
done
clear
View Answer play_arrow
question_answer 142) The equation to a pair of opposite sides of a parallelogram are \[30\sqrt{3}m\] and \[10\sqrt{3}m\], the equation to its diagonals are :
A)
\[\left( \text{a},\text{b}+\text{c} \right),\left( \text{b},\text{c}+\text{a} \right),\left( \text{c},\text{a}+\text{b} \right)\]and \[abc\]
done
clear
B)
\[~{{\text{a}}^{\text{2}}}+{{\text{b}}^{\text{2}}}+{{\text{c}}^{\text{2}}}\] and \[\text{ab}+\text{bc}+\text{ca}\]
done
clear
C)
\[y=2x+c\] and \[x+2y=3,3x+4y=7,2x+3y=4\]
done
clear
D)
\[4x+5y=6\] and y \[xy=0\]
done
clear
View Answer play_arrow
question_answer 143) The equation of the chord of the circle, \[{{x}^{2}}-5x+6=0\] having \[{{y}^{2}}-6y+5=0\] as its mid-point, is:
A)
\[x+4y=13\]
done
clear
B)
\[y=4x-7\]
done
clear
C)
\[4x+y=13\]
done
clear
D)
\[4y=x-7\]
done
clear
View Answer play_arrow
question_answer 144) A circle of radius 5 touches another circle \[4x+y=13\]at (5, 5),then its equation is :
A)
\[y=4x-7\]
done
clear
B)
\[y-4x=13\]
done
clear
C)
\[y+4x-7\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 145) The equation of the latus-rectum of the parabola \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] is equal to :
A)
\[({{x}_{1}},{{y}_{1}})\]
done
clear
B)
\[x{{y}_{1}}+y{{x}_{1}}={{a}^{2}}\]
done
clear
C)
\[{{x}_{1}}+{{y}_{1}}=a\]
done
clear
D)
\[x{{x}_{1}}+y{{y}_{1}}=x_{1}^{2}+y_{1}^{2}\]
done
clear
View Answer play_arrow
question_answer 146) The length of major and minor axis of an ellipse are 10 and 8 respectively and its major axis along the y-axis the equation of the ellipse referred to its centre as origin is :
A)
\[x{{x}_{1}}+y{{y}_{1}}={{a}^{2}}\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}-2x-4y-20=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+18x+16y+120=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}-18x-16y+120=0\]
done
clear
View Answer play_arrow
question_answer 147) The point of intersection of tangents at the ends of the latus-rectum of the parabola \[{{x}^{2}}+{{y}^{2}}-18x+16y+120=0\] is equal to :
A)
(1,0)
done
clear
B)
\[{{x}^{2}}+4x+2y=0\]
done
clear
C)
\[2y+3=0\]
done
clear
D)
\[3y=2\]
done
clear
View Answer play_arrow
question_answer 148) Eccentricity of the parabola \[2y=3\] is equal to :
A)
\[3y+2=0\]
done
clear
B)
\[\frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{16}=1\]
done
clear
C)
\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{25}=1\]
done
clear
D)
\[\frac{{{x}^{2}}}{100}+\frac{{{y}^{2}}}{64}=1\]
done
clear
View Answer play_arrow
question_answer 149) The angle between the lines \[\frac{{{x}^{2}}}{64}+\frac{{{y}^{2}}}{100}=1\]and \[{{y}^{2}}=4x\] is equal to :
A)
\[(-1,0)\]
done
clear
B)
\[\left( 0,1 \right)\]
done
clear
C)
\[\left( 0,-\text{l} \right)\]
done
clear
D)
\[{{x}^{2}}-4x-4y+4=0\]
done
clear
View Answer play_arrow
question_answer 150) \[e=0\]is equal to:
A)
\[e=1\]
done
clear
B)
\[e>4\]
done
clear
C)
0
done
clear
D)
\[e=4\]
done
clear
View Answer play_arrow
question_answer 151) If the points whose position vectors are\[\frac{x}{1}=\frac{y}{0}=\frac{z}{-1}\] and \[\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\]lie on a plane, then \[{{\cos }^{-1}}\left( \frac{1}{5} \right)\]is equal to :
A)
\[{{\cos }^{-1}}\left( \frac{1}{3} \right)\]
done
clear
B)
\[{{\cos }^{-1}}\left( \frac{1}{2} \right)\]
done
clear
C)
\[{{\cos }^{-1}}\left( \frac{1}{4} \right)\]
done
clear
D)
\[(a-b).(b-c)\times (c-a)\]
done
clear
View Answer play_arrow
question_answer 152) If \[2a.b\times c\] and \[a.b\times c\] \[a.b\] and \[3\hat{i}-2\hat{j}-\hat{k},2\hat{i}+3\hat{j}-4\hat{k},-\hat{i}+\hat{j}+2\hat{k}\] are non-coplanar vectors, then \[4\hat{i}+5\hat{j}+\lambda \hat{k}\]is equal to:
A)
-1
done
clear
B)
0
done
clear
C)
1
done
clear
D)
4
done
clear
View Answer play_arrow
question_answer 153) In \[\lambda \]if \[-\frac{146}{17}\], then\[\frac{146}{17}\] equals :
A)
\[-\frac{17}{146}\]
done
clear
B)
\[\frac{17}{146}\]
done
clear
C)
\[\left| \begin{matrix} a & {{a}^{2}} & 1+{{a}^{3}} \\ b & {{b}^{3}} & 1+{{b}^{3}} \\ c & {{c}^{3}} & 1+{{c}^{3}} \\ \end{matrix} \right|=0\]
done
clear
D)
\[(1,a,{{a}^{2}})\]
done
clear
View Answer play_arrow
question_answer 154) Let \[(1,b,{{b}^{2}})\]and a unit vector \[(1,c,{{c}^{2}})\] be coplanar, if \[\text{abc}\] is perpendicular to \[\Delta ABC\] then \[2\overrightarrow{AC}=3\overrightarrow{CB}\]is equal to:
A)
\[2\overrightarrow{OA}+3\overrightarrow{OB}\]
done
clear
B)
\[4\overrightarrow{OC}\]
done
clear
C)
\[-\overrightarrow{OC}\]
done
clear
D)
\[\overrightarrow{OC}\]
done
clear
View Answer play_arrow
question_answer 155) \[4\overrightarrow{OC}\]is equal to :
A)
\[\overrightarrow{a}\text{ }=\text{2\hat{i}}+\text{\hat{j}+ \hat{k}},\text{ }\overrightarrow{\text{b}}=\text{\hat{i}}+\text{2\hat{j}}-\text{\hat{k}}\]
done
clear
B)
\[\overrightarrow{c}\]
done
clear
C)
\[\overrightarrow{c}\]
done
clear
D)
0
done
clear
View Answer play_arrow
question_answer 156) If\[\overrightarrow{a}\text{ }=\text{2\hat{i}}+\text{\hat{j}+ \hat{k}},\text{ }\overrightarrow{\text{b}}=\text{\hat{i}}+\text{2\hat{j}}-\text{\hat{k}}\], when \[\overrightarrow{c}\], where \[\frac{1}{\sqrt{2}}(-\hat{j}+\hat{k})\] is greatest integer function, then \[\frac{1}{\sqrt{3}}(-\hat{i}-\hat{j}-\hat{k})\] is equal to :
A)
-1
done
clear
B)
1
done
clear
C)
does not exist
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 157) The function \[\frac{1}{\sqrt{5}}(\hat{i}-2\hat{j})\],\[\frac{1}{\sqrt{3}}(\hat{i}-\hat{j}-\hat{k})\]where\[\underset{x\to 1}{\mathop{\lim }}\,(1-x)\tan \left( \frac{\pi x}{2} \right)\]assumes its minimum value only at one point, if :
A)
\[\frac{\pi }{2}\]
done
clear
B)
\[\pi \]
done
clear
C)
\[\frac{2}{\pi }\]
done
clear
D)
\[f(x)=\frac{\sin [x]}{[x]}\]
done
clear
View Answer play_arrow
question_answer 158) \[[x]\ne 0\]
A)
exists and is equals \[[x]\]
done
clear
B)
exists and is equals \[\underset{x\to 0}{\mathop{\lim }}\,f[x]\]
done
clear
C)
does not exist because \[f(x)=|px-q|+r|x|\]
done
clear
D)
does not exist because left hand limit is not equal to right hand limit
done
clear
View Answer play_arrow
question_answer 159) Differential coefficient of sec \[x\in (-\infty ,\infty )\] with respect to \[p>0,q>0,r>0\] at \[p\ne q\]is equal to :
A)
2
done
clear
B)
4
done
clear
C)
6
done
clear
D)
1
done
clear
View Answer play_arrow
question_answer 160) The function \[q\ne r\]increases, if :
A)
\[r\ne p\]
done
clear
B)
\[p=q=r\]
done
clear
C)
\[\underset{x\to 1}{\mathop{\lim }}\,\frac{\sqrt{1-\cos 2(x-1)}}{x-1}\]
done
clear
D)
\[\sqrt{2}\]
done
clear
View Answer play_arrow
question_answer 161) \[-\sqrt{2}\] is equal to :
A)
\[x-1\to 0\]
done
clear
B)
\[{{\sec }^{-1}}\frac{1}{2{{x}^{2}}-1}\]
done
clear
C)
\[\sqrt{1-{{x}^{2}}}\]
done
clear
D)
\[x=\frac{1}{2}\]
done
clear
View Answer play_arrow
question_answer 162) Area bounded by the curve \[f(x)={{\sin }^{4}}x+{{\cos }^{4}}x\] and the straight line \[0<x<\frac{\pi }{8}\], is equal to :
A)
\[\frac{\pi }{4}<x<\frac{3\pi }{8}\] sq. units
done
clear
B)
\[\frac{3\pi }{8}<x<\frac{5\pi }{8}\]sq. units
done
clear
C)
\[\frac{5\pi }{8}<x<\frac{3\pi }{4}\]sq. units
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 163) The solution of the differential equation\[\int{\sqrt{1+\sin \frac{x}{2}}}dx\] is :
A)
\[\frac{1}{4}\left[ \cos \frac{x}{4}-\sin \frac{x}{4} \right]+C\]
done
clear
B)
\[4\left[ \cos \frac{x}{4}-\sin \frac{x}{4} \right]+C\]
done
clear
C)
\[4\left[ \sin \frac{x}{4}-\cos \frac{x}{4} \right]+C\]
done
clear
D)
\[4\left[ \sin \frac{x}{4}+\cos \frac{x}{4} \right]+C\]
done
clear
View Answer play_arrow
question_answer 164) In a binomial distribution, mean is 3 and standard deviation is \[x=4y\], then the probability distribution is :
A)
\[x=4y-2\]
done
clear
B)
\[\frac{8}{9}\]
done
clear
C)
\[\frac{9}{8}\]
done
clear
D)
\[\frac{4}{3}\]
done
clear
View Answer play_arrow
question_answer 165) The probability of India winning a test match against West indies is \[({{x}^{2}}-y{{x}^{2}})\frac{dy}{dx}+{{y}^{2}}+x{{y}^{2}}=0\] assuming independence from match to match the probability that in a 5 match series Indias second win occurs at the third test, is :
A)
2/3
done
clear
B)
½
done
clear
C)
1/4
done
clear
D)
1/8
done
clear
View Answer play_arrow
question_answer 166) If both the regression lines intersect perpendicularly, then :
A)
\[\log \left( \frac{x}{y} \right)=\frac{1}{x}+\frac{1}{y}+c\]
done
clear
B)
\[\log \left( \frac{y}{x} \right)=\frac{1}{x}+\frac{1}{y}+c\]
done
clear
C)
\[\log (xy)=\frac{1}{x}+\frac{1}{y}+c\]
done
clear
D)
\[\log (xy)+\frac{1}{x}+\frac{1}{y}=c\]
done
clear
View Answer play_arrow
question_answer 167) If\[\frac{3}{2}\], \[{{\left( \frac{3}{4}+\frac{1}{4} \right)}^{12}}\], and \[{{\left( \frac{1}{4}+\frac{3}{4} \right)}^{12}}\], then the coefficient of correlation is :
A)
0.1
done
clear
B)
0.3
done
clear
C)
0.2
done
clear
D)
0.1
done
clear
View Answer play_arrow
question_answer 168) For any two independent events \[{{\left( \frac{1}{4}+\frac{3}{4} \right)}^{9}}\] anc \[{{\left( \frac{3}{4}+\frac{1}{4} \right)}^{9}}\], \[\frac{1}{2}\]) is equal to :
A)
\[r<-1\]
done
clear
B)
\[r=-1\]
done
clear
C)
\[r=0\]
done
clear
D)
none of these
done
clear
View Answer play_arrow
question_answer 169) The degree of the differential equation \[r=\frac{1}{2}\]is equal to:
A)
1
done
clear
B)
2
done
clear
C)
3
done
clear
D)
6
done
clear
View Answer play_arrow
question_answer 170) \[\overline{x}+\overline{y}=0\] is equal to :
A)
\[\sum {{x}_{i}}{{y}_{i}}=12,{{\sigma }_{x}}=2,{{\sigma }_{y}}=3\]
done
clear
B)
0
done
clear
C)
1
done
clear
D)
\[n=10\]
done
clear
View Answer play_arrow