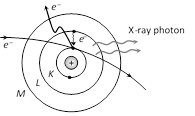
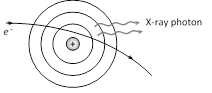
 To fill this vacancy electrons from higher shells jump to fill the created vacancies, we know that when an electron jumps from a higher energy orbit
\[{{E}_{1}}\] to lower energy orbit \[{{E}_{2}}\], it radiates energy \[({{E}_{1}}-{{E}_{2}})\]. Thus this energy difference is radiated in the form of X-rays of very small but definite wavelength which depends upon the target material. The X-ray spectrum consists of sharp lines and is called characteristic X-ray spectrum.
(1) K, L, M, ... series : If the electron striking the target eject an electron from the K-shell of the atom, a vacancy is created in the K-shell. Immediately an electron from one of the outer shell, say L-shell jumps to the K-shell, emitting an X-ray photon of energy equal to the energy difference between the two shells. Similarly, if an electron from the M-shell jumps to the K-shell, X-ray photon of higher energy is emitted. The X-ray photons emitted due to the jump of electron from the L, M, N shells to the K-shells gives \[{{K}_{\alpha }},\,\,{{K}_{\beta }},\,\,{{K}_{\gamma }}\] lines of the K-series of the spectrum.
To fill this vacancy electrons from higher shells jump to fill the created vacancies, we know that when an electron jumps from a higher energy orbit
\[{{E}_{1}}\] to lower energy orbit \[{{E}_{2}}\], it radiates energy \[({{E}_{1}}-{{E}_{2}})\]. Thus this energy difference is radiated in the form of X-rays of very small but definite wavelength which depends upon the target material. The X-ray spectrum consists of sharp lines and is called characteristic X-ray spectrum.
(1) K, L, M, ... series : If the electron striking the target eject an electron from the K-shell of the atom, a vacancy is created in the K-shell. Immediately an electron from one of the outer shell, say L-shell jumps to the K-shell, emitting an X-ray photon of energy equal to the energy difference between the two shells. Similarly, if an electron from the M-shell jumps to the K-shell, X-ray photon of higher energy is emitted. The X-ray photons emitted due to the jump of electron from the L, M, N shells to the K-shells gives \[{{K}_{\alpha }},\,\,{{K}_{\beta }},\,\,{{K}_{\gamma }}\] lines of the K-series of the spectrum.
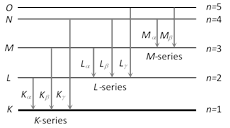 If the electron striking the target ejects an electron from the L-shell of the target atom, an electron from the M, N ... shells jumps to the L-shell so that X-rays photons of lesser energy are emitted.
These photons form the L-series of the spectrum. In a similar way the formation of M series, N series etc. may be explained.
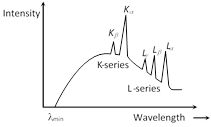
(2) Intensity-wavelength graph : At certain sharply defined wavelengths, the intensity of X-rays is very large as marked \[{{K}_{\alpha }},\,\,{{K}_{\beta }}\] as shown in figure. These X-rays are known as characteristic X-rays. At other wavelengths the intensity varies gradually and these X-rays are called continuous X-rays.
If the electron striking the target ejects an electron from the L-shell of the target atom, an electron from the M, N ... shells jumps to the L-shell so that X-rays photons of lesser energy are emitted.
These photons form the L-series of the spectrum. In a similar way the formation of M series, N series etc. may be explained.
(2) Intensity-wavelength graph : At certain sharply defined wavelengths, the intensity of X-rays is very large as marked \[{{K}_{\alpha }},\,\,{{K}_{\beta }}\] as shown in figure. These X-rays are known as characteristic X-rays. At other wavelengths the intensity varies gradually and these X-rays are called continuous X-rays.
 (1) Minimum wavelength : When the electron looses whole of it's energy in a single collision with the atom, an X-ray photon of maximum energy h\[{{v}_{\max }}\] is emitted i.e.\[\frac{1}{2}m{{v}^{2}}=eV=h{{\nu }_{\max }}=\frac{hc}{{{\lambda }_{\min }}}\]
where v = velocity of electron before collision with target atom, V = potential difference through which electron is accelerated, c = speed of light \[=3\times {{10}^{8}}\,m/s\]
Maximum frequency of radiations (X-rays) \[{{\nu }_{\max }}=\frac{eV}{h}\]
Minimum wavelength = cut off wavelength of X-ray
\[{{\lambda }_{\min }}=\frac{hc}{eV}=\frac{12375}{V}{\AA}\]
(2) Intensity wavelength graph : The continuous X-ray spectra consist of all the wavelengths over a given range. These wavelength are of different intensities. Following figure shows the intensity variation of different wavelengths for various accelerating voltages applied to X-ray tube.
(1) Minimum wavelength : When the electron looses whole of it's energy in a single collision with the atom, an X-ray photon of maximum energy h\[{{v}_{\max }}\] is emitted i.e.\[\frac{1}{2}m{{v}^{2}}=eV=h{{\nu }_{\max }}=\frac{hc}{{{\lambda }_{\min }}}\]
where v = velocity of electron before collision with target atom, V = potential difference through which electron is accelerated, c = speed of light \[=3\times {{10}^{8}}\,m/s\]
Maximum frequency of radiations (X-rays) \[{{\nu }_{\max }}=\frac{eV}{h}\]
Minimum wavelength = cut off wavelength of X-ray
\[{{\lambda }_{\min }}=\frac{hc}{eV}=\frac{12375}{V}{\AA}\]
(2) Intensity wavelength graph : The continuous X-ray spectra consist of all the wavelengths over a given range. These wavelength are of different intensities. Following figure shows the intensity variation of different wavelengths for various accelerating voltages applied to X-ray tube.
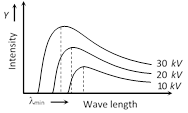 For each voltage, the intensity curve starts at a particular minimum wavelength \[({{\lambda }_{\min }})\]. Rises rapidly to a maximum and then drops gradually.
The wavelength at which the intensity is maximum depends on the accelerating voltage, being shorter for higher voltage and vice-versa.
For each voltage, the intensity curve starts at a particular minimum wavelength \[({{\lambda }_{\min }})\]. Rises rapidly to a maximum and then drops gradually.
The wavelength at which the intensity is maximum depends on the accelerating voltage, being shorter for higher voltage and vice-versa. 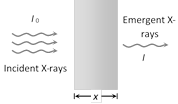 \[\mu \propto {{\lambda }^{3}};\,(\lambda \]= Wavelength of X-ray)
\[\mu \propto {{\bar{\nu }}^{3}}\,(\nu =\] Frequency of X-ray)
\[\mu \propto {{Z}^{4}}\,(Z=\]Atomic number of target)
\[\mu \propto {{\lambda }^{3}};\,(\lambda \]= Wavelength of X-ray)
\[\mu \propto {{\bar{\nu }}^{3}}\,(\nu =\] Frequency of X-ray)
\[\mu \propto {{Z}^{4}}\,(Z=\]Atomic number of target) 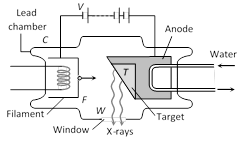 (4) The filament is heated by passing the current through it. A high potential difference (\[\approx \] 10 kV to 80 kV) is applied between the target and cathode to accelerate the electrons which are emitted by filament. The stream of highly energetic electrons are focussed on the target.
(5) Most of the energy of the electrons is converted into heat (above 98%) and only a fraction of the energy of the electrons (about 2%) is used to produce X-rays.
(6) During the operation of the tube, a huge quantity of heat is produced in this target, this heat is conducted through the copper anode to the cooling fins from where it is dissipated by radiation and convection.
(7) Control of intensity of X-rays : Intensity implies the number of X-ray photons produced from the target. The intensity of X-rays emitted is directly proportional to the electrons emitted per second from the filament and this can be increased by increasing the filament current. So intensity of X-rays \[\propto \] Filament current
(8) Control of quality or penetration power of X-rays : Quality of X-rays implies the penetrating power of X-rays, which can be controlled by varying the potential difference between the cathode and the target. For large potential difference, energy of bombarding electrons will be large and hence larger is the penetration power of X-rays.
Types of X-rays
(4) The filament is heated by passing the current through it. A high potential difference (\[\approx \] 10 kV to 80 kV) is applied between the target and cathode to accelerate the electrons which are emitted by filament. The stream of highly energetic electrons are focussed on the target.
(5) Most of the energy of the electrons is converted into heat (above 98%) and only a fraction of the energy of the electrons (about 2%) is used to produce X-rays.
(6) During the operation of the tube, a huge quantity of heat is produced in this target, this heat is conducted through the copper anode to the cooling fins from where it is dissipated by radiation and convection.
(7) Control of intensity of X-rays : Intensity implies the number of X-ray photons produced from the target. The intensity of X-rays emitted is directly proportional to the electrons emitted per second from the filament and this can be increased by increasing the filament current. So intensity of X-rays \[\propto \] Filament current
(8) Control of quality or penetration power of X-rays : Quality of X-rays implies the penetrating power of X-rays, which can be controlled by varying the potential difference between the cathode and the target. For large potential difference, energy of bombarding electrons will be large and hence larger is the penetration power of X-rays.
Types of X-rays
| Hard X-rays | Soft X-rays |
| More penetration power | Less penetration power |
| More frequency of the order of \[\approx {{10}^{19}}\,Hz\] | Less frequency of the order of \[\approx {{10}^{16}}\,Hz\] |
| more...
(1) X-rays were discovered by scientist Rontgen thats why they are also called Rontgen rays.
(2) Rontgen discovered that when pressure inside a discharge tube is kept \[{{10}^{-3}}\,mm\] of Hg and potential difference is kept 25 kV, then some unknown radiations (X-rays) are emitted by anode.
(3) There are three essential requirements for the production of X-rays.
(i) A source of electron
(ii) An arrangement to accelerate the electrons
(iii) A target of suitable material of high atomic weight and high melting point on which these high speed electrons strike.
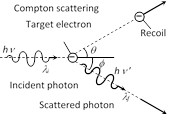
(1) The scattering of a photon by an electron is called Compton effect.
(2) The energy and momentum is conserved.
(3) Scattered photon will have less energy (more wavelength) as compare to incident photon (less wavelength).
(4) The energy lost by the photon is taken by electron as kinetic energy.
(5) The change in wavelength due to Compton effect is called Compton shift. Compton shift \[{{\lambda }_{f}}-{{\lambda }_{i}}=\Delta \lambda =\frac{h}{{{m}_{0}}c}(1-\cos \varphi )\]
If \[\phi ={{0}^{o}},\,\,\Delta \lambda =0\]
\[\phi ={{90}^{o}},\,\,\Delta \lambda =\frac{h}{{{m}_{0}}c}=0.24\,nm\] \[\varphi ={{180}^{o}},\,\Delta \lambda =\frac{2h}{{{m}_{0}}c}=\,0.48nm\] (called Compton wave length)
(1) \[h\nu =h{{\nu }_{0}}+{{K}_{\max }}\] and \[{{K}_{\max }}=e{{V}_{0}}\]
(2) \[{{K}_{\max }}=e{{V}_{0}}=h(\nu -{{\nu }_{0}})\]\[\Rightarrow \]\[\frac{1}{2}mv_{\max }^{2}=h(\nu -{{\nu }_{0}})\]
(3) \[{{v}_{\max }}=\sqrt{\frac{2h(\nu -{{\nu }_{0}})}{m}}\]
(4) \[{{K}_{\max }}=\frac{1}{2}mv_{\max }^{2}=e{{V}_{0}}=hc\,\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)=hc\,\left( \frac{{{\lambda }_{0}}-\lambda }{\lambda {{\lambda }_{0}}} \right)\]
(5) \[{{v}_{\max }}=\sqrt{\frac{2hc}{m}\frac{\left( {{\lambda }_{0}}-\lambda \right)}{\lambda {{\lambda }_{0}}}}\]
(6) \[{{V}_{0}}=\frac{h}{e}(\nu -{{\nu }_{0}})=\frac{hc}{e}\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)=12375\,\left( \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right)\]
(1) Effect of intensity : If the intensity of light is increased (while it's frequency is kept the same) the current levels off at a higher value, showing that more electrons are being emitted per unit time. But the stopping potential \[{{V}_{0}}\] doesn't change i.e.
Intensity \[\propto \] no. of incident photon \[\propto \] no. of emitted photoelectron per time \[\propto \] photo current
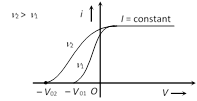
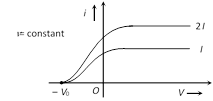 (2) Effect of frequency : If frequency of incident light increases, (keeping intensity is constant) stopping potential increases but their is no change in photoelectric current
(2) Effect of frequency : If frequency of incident light increases, (keeping intensity is constant) stopping potential increases but their is no change in photoelectric current
 Current Affairs CategoriesArchive
Trending Current Affairs
You need to login to perform this action. |