Current Affairs 6th Class

  The Neolithic Revolution   Summary         1.            The period when man started practicing agriculture from being a hunter-gatherer is known as the Neolithic Revolution. 2.            At this time, man also learnt to keep animals. They began to tame lots of different animals and eventually they started keeping herds of sheep, goats and cattle. Animals were also a source of food. 3.            Slowly, the wandering lifestyle changed and they built huts near water sources. 4.            Archaeologists have found evidence of farmers and herders all over the subcontinent. So, we know that a variety of crops were grown and animals were domesticated. 5.            They made tools called celts which had edges that were sharpened by grinding. 6.            The wheel was probably invented around 7,000 BCE. 7.            Mehrgarh provides the earliest evidence of transition from hunting and gathering to agriculture and animal domestication.   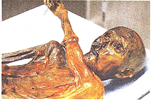In September 1991, two German tourists, Helmut and Erika Simon, found a well-preserved dead body of a man who lived about 5,300 years ago He was discovered in a glacier of the Otztal Alps, near the border between Austria Italy. He has been nicknamed 'Otzi the Iceman' after the valley of his discovery the body has been extensively examined, X-rayed, measured and dated. Analysis of Otz?s tooth enamel shows that he spent his childhood near the present village of Feldthurns, Italy. He had 57 tattoos, some of which were located on or near acupuncture points. Scientists believe that these tattoos indicate an early type of acupuncture. Items found with him include a copper axe with a\[ye{{w}^{1}}\]handle, a flint-bladed knife with an \[as{{h}^{2}}\]handle and a\[quive{{r}^{3}}\]of 14 arrows with\[viburnu{{m}^{4}}\]and dogwood5 shafts. Otzi is a natural mummy and belongs to the Chalcolithic Age.     As we already know, about 10,000 years ago, the climate became warmer. Warmer weather made life easier and population began to grow. People could not find enough food by hunting and gathering. They needed a new way to survive. Thus they started farming and animal domestication. The period during which man turned from hunting and food gathering to agriculture is so important that it is known as the Neolithic Revolution. It was a gradual process which took place over more...

                                           The Lives of the Hunter-Gatherers   Summary   1.            The hunter-gatherers were the earliest humans on the earth. These early humans hunted animals and gathered wild plants for food. 2.            The hunter-gatherers were nomads moving from one place to another. 3.            The early humans made simple things using material found in nature. They used wood/ bones, stones, antlers, tusks and shells to make simple tools. 4.            Different types of tools have been discovered. It took thousands of years before a stone tool changed its shape and was made more efficient. 5.            The places where humans lived are called habitation sites. These were mostly near rivers or lakes. The places where stone tools were made are called factory sites. 6.            Striking paintings have been found on the ceilings, floors and walls of caves and rock shelters. The most common subject of the art was hunting scenes, which were beautifully and realistically depicted. 7.            The climate became warmer as the ice caps were shrinking. More grasses and trees grew and with them grew the number of grass eating animals. Early humans now began to think of rearing these animals.     Have you ever wondered how the earliest man on the earth looked like? Nobody knows for sure but researchers and studies by experts show that man evolved from apes. Then, over 5 million years ago, some apes in Africa learnt to walk upright. This was a long and gradual evolutionary process. It took millions of years before apes evolved into the 'modern7 humans of today.   THE EARLIEST PEOPLE AND THEIR WAY OF LIFE The hunter-gatherers were the earliest humans on the earth. These early humans hunted animals and gathered wild plants for food. Their lives were not very different from those of other animals. They spent all day prowling about in the jungles and swamps, protecting themselves from other beasts and searching for food. Life consisted of collecting fruits, seeds, nuts, leaves, digging up roots, trapping animals and birds for food and killing them with stone tools. They had to take whatever nature offered them. Securing food was not easy. They had to be very alert, quick and strong. Gradually they learnt to distinguish which berries were poisonous, which parts of the plants were edible, which animals were easy to kill more...

  History - When, Where and How     Summary   1.           History is a study of the past. It helps us to understand change and how it came about and how the society we live in came to be. 2.           Many geographical location in India were inhabited by the early settlers. Humans began settlements near rivers. This gave them access to water. Historians have identified many such sites. 3.           The history of a place is shaped by the location and geography of that particular place.  The physical features of the Indian subcontinent have greatly influenced its history. 4.           Sources of history give us information about the past. Once we get the information, the past can be reconstructed. 5.           Archaeologists are people who excavate to find evidence of the past. Archaeologist evidence includes cave paintings, coins, inscriptions, monuments and burials. 6.           Literary sources consist of biographies, manuscripts, travelogues, religious and secular literature.    7.           The birth of Christ is used as a reference point to measure time in years.       History is a study of the past. It comes from the Greek word historia meaning information acquired by inquiry. It is the true story of mankind and man's adventures on the earth. No one knows exactly when it began but it is still going on at the present time.   WHAT IS HISTORY   This is a very frequently asked question. Our past and present are inseparable. One cannot divorce the past from the present because the past shapes the future. It helps us to understand change and how it came about and how the society we live in came to be.   Things around us just did not happen. They happened over time. We cannot understand the things and the ways of life today unless we know how they developed. When you are reading this book, you are using paper. Where has this paper come from? Who was the first to make paper? The Egyptians were the first to start the art of papermaking sometime around 3500 BCE. It was made from papyrus reeds. The word "paper" more...

Food Production and Management   Synopsis  

• Agriculture is the science or practice of growing crops.

 

• Plants of the same kind are grown and cultivated at one place on a large scale are called crops.

 

• There are three main crop seasons -

(i) Kharif (June-September), e.g., rice, jute, maize, groundnut and cotton. (ii) Rabi (October-March), e.g., wheat, mustard, potato, barley and gram. (iii) Summer crops.  

• The steps involved in cultivating a crop are as follows.

 

• Ploughing, levelling and manuring the soil.

 

• Sowing seeds at the correct depth and with right spaces between them. Some seeds are sown in nurseries and the seedlings are then transplanted to the main field.

 

• Improving soil fertility by adding manure and chemical fertilizers and also by adopting methods like crop rotation and leaving the field fallow.

 

• Ensuring irrigation at the right time.

 

• Protecting crops from weeds, pests and diseases either by using chemicals or by using natural methods.

 

• Harvesting, threshing and winnowing.

 

• Legumes are often used in crop rotation, because the nitrogen fixing bacteria which live in their roots improve soil fertility.

 

• Nitrogen fixation is a part of the nitrogen cycle, which is, continued cycling of nitrogen from the air to the soil and to living organisms.

 

• Grains are stored in silos or god owns that have been fumigated. Buffer stock is maintained for emergencies.

 

• Scientists have developed hybridisation processes to grow disease resistant varieties of plants. The earliest success is the production of high-yielding varieties of plants which led to increase in the production of food crops. This is often referred to as the Green Revolution.

 

• The branch of agriculture dealing with the rearing of farm animals is called animal husbandry.

 

• Animals give us milk, meat and eggs. Animal products are an excellent source of protein. Animal proteins are superior to plant proteins. Egg white contains the protein albumen.

Science in Everyday Life  

• Science helps us to acquire knowledge about new things and happenings around us. Rapid development and improvement have come about through science and its various applications. Following are few a scientists with their remarkable discoveries:

Chief Scientists                                    Work   Nagarjuna                                                Indian mathematician; inventor of the digit zero Edward Jenner                                     Discovered numerous methods to cure diseases Edward Jenner                                     Discovered the world's first vaccine Alexander Fleming                             Discovered world's first antibiotic- penicillin—which cured various bacterial infections. Madame Curie                                      Discovered radium and polonium Antonie Van                                            Invented the microscope, an instrument, Leeuwenhoek                                       useful for studying various types of germs, examining the blood and so on. Louis Pasteur                                        Discovered methods of preserving milk, jam, etc., and pasteurization Jagadish Chandra Bose                 Studied the sensitivity of plants in detail  

• Other Modern Scientists: Sir C. V. Raman, S Ramanujan, S. N. Bose, M. N. Saha, D.N. Wadia, B. Sahni, P. Maheshwari, G. N. Ramachandran, T.R. Sheshadri, Homi Bhabha and Vikram Sarabhai.

Things Around Us All the objects are made up of one or more materials. Materials may be classified in two categories: (1) Naturally occurring materials (2) Man made materials   NATURALLY OCCURRING MATERIALS · Examples are coal, wood, rocks, minerals, water, gold, petroleum, etc. MAN MADE MATERIALS · Examples are glass, plastic, fertiliser, paper, stainless steel, etc. · The entire universe is made up of matter. All materials and substances are made up of matter. Anything that we can see, touch, smell or taste is matter. · Anything that has mass and occupies space is called matter. · Matter can exist in three different states, i.e., solid, liquid and gaseous. (1) Solid - Example: wood (2) Liquid - Example: water (3) Gas - Example: oxygen · By changing the temperature, the state of the matter can be changed. Some forms of matter can be changed from one state to another and then can be reverted to the original state. · The process of changing a solid into a liquid by heating is called melting. The melting of a substance takes place at a fixed temperature. This temperature is called the melting point of that substance. · Ice melts at \[0{}^\circ C.\] Ice on melting forms water. On boiling water, forms steam. Steam is in a gaseous state. Most of the liquids keep on changing slowly into vapours at all temperatures. This process is called evaporation. · On continued heating, the temperature of a liquid rises and starts boiling at a fixed temperature. This temperature is called the boiling point of the liquid. Water boils at \[100{}^\circ C.\] · The process of changing vapour or a gas into a liquid by cooling is called condensation. For example, when water boils in a vessel, water droplets are formed due to cooling of steam on the lid and get converted into water. · The process of changing a liquid into a solid on cooling is called freezing, as water on cooling turns into ice. \

• Gold, copper, iron and silver change into liquid and gaseous states at high temperatures.
• Materials are classified based on their state, their solubility in water, their behaviour towards a magnet, their density with respect to water, their transparency or opaqueness, etc.
• Things around us seem to be of an endless variety. Many objects and materials are made up of only a few basic units (building blocks). There are naturally occurring basic units on the Earth. These basic units are called elements. A few more elements have also been prepared by scientists. Now there are more than 110 known elements. These elements are said to be the building blocks of materials like the brick, which are the building blocks of a building.
• Some of the common elements are hydrogen, helium, carbon, nitrogen, oxygen, sodium, magnesium, aluminium, silicon, phosphorus, sulphur, zinc, bromine, silver, tin, iodine, gold and mercury. Most of the common materials are made up of one or more than more...

Separation of Substances

• A mixture refers to the physical combination of two or more substances in which their individual identities are retained. The components, whether two or more, can be separated. For example, separating small pieces of stone from wheat and rice, peeling off the skin of a banana before eating it, separating cream from milk, etc.
• Separation of mixtures into their constituents is often necessary for several reasons. These are as follows:
• To remove undesirable substances
• To remove harmful substances
• To obtain a pure sample of a substance
• To obtain useful components

  METHODS OF SEPARATION

• Winnowing: Winnowing is a simple method of cleaning food materials from a mixture. It separates the grains from the husk because one particle is lighter than the other. Farmers thresh wheat or paddy to loosen the grains from the chaff. This mixture is made to fall from a height. The breeze blows away the chaff, while the grains fall almost vertically. The chaff forms a separate heap at a little distance away from the heap of grains.
• Hand picking: If the mixture comprises solids of different colours, shape or sizes, it can be separated by hand picking. For example, picking stone pebbles from rice, pulses, wheat or other food grains. This method is normally used when the quantity of impurities as well as the material to be cleaned is small in quantity.
• Sieving: Sieving is possible only when the particles of a mixture are of different sizes. This method is used specially for purifying the mixtures of food materials from undesirable materials.
• Separation with magnet: Magnets attract iron. Thus, good quality magnets are used to separate iron from a mixture.
• Sedimentation and Decantation: Insoluble solids, i.e., solids that do not dissolve in a liquid can be separated from it by processes like sedimentation and decantation.

(a) Sedimentation is the process of settling down of an insoluble solid in a liquid at the bottom of a container. (b) Decantation is the process of separating out the clear liquid on the top without disturbing the sediment. This process is only done after sedimentation. For example, a mixture of sand and water is left for a while. The sand settles down and forms a layer at the bottom, this is sedimentation. And when clear water is poured into another vessel without disturbing the sand at the bottom, it is called decantation.

• If a solid is soluble in water or two liquids are miscible (or soluble into each other) then, the process of sedimentation cannot be used for separation. Mixture of water and sugar and mixture of kerosene oil and petrol represent a solid soluble in water and two miscible liquids, respectively.
• Two immiscible (or insoluble) liquids like a mixture of water and kerosene oil can be separated by decantation and by using a separating funnel. This method of separation is based on the property of the mixture that one constituent is heavier (water more...

Measurement

• Measurement is one of the most useful processes in science and in our daily life. Without actual measurements, we cannot make correct judgments about a given object. It is not always easy to find out the length, area, volume or mass of different objects just by looking at them.
• For the sake of uniformity, scientists all over the world have accepted certain standard units for measuring different quantities. For example

Quantity	Standard Unit
Length	Meter
Mass	Kilogram
Time	Second

• Standard unit of length                                               : Metre
• Meaning of length                                                          : Metre can be used as a unit to measure the length of a room, the height of a tree or a building or length and breadth of a playground.

• Short form of standard unit                                      : m
• Other standard units                                                    : 10 millimeters (mm) = 1 centimeter (cm)

                                                                                                            : 100 cm = 1 meter (m)                                                                                                             : 1000 m = 1 Kilometer (Km)

• Standard unit of area                                                    : \[Metr{{e}^{2}}\]
• Meaning of area                                                               : Area is the measure of surface of an object
• Short form of standard unit                                      : \[{{m}^{2}}\]
• Another unit of standard unit                                  : \[1\,acre=100\,{{m}^{2}}\]

                                                                                                              : \[1\,hectare=100\,acre=1000\,{{m}^{2}}\]

• Standard unit of volume                                               : \[\begin{array}{*{35}{l}}
• Metr{{e}^{3}}  \\
• \end{array}\]or cubic meter
• Meaning of volume                                                          : The space occupied by an object is called its volume. The space availablein a container is called its capacity. In fact, the capacity of a container is its inner volume.

• Short form of standard unit                                        : \[{{m}^{3}}\]
• Other standard units                                                       : When the object is small, instead of considering \[{{m}^{3}}\] as a unit, more...

Changes Around Us  

• From morning till night, we observe many changes around us. For example, sudden change in the weather, rainfall, flowering of plants, germination of seeds, ripening of fruits, drying of clothes, change of day into night, melting of ice, evaporation of water, burning of fuels, cooking of rice, formation of curd from milk, rusting of iron, burning of fireworks, etc. Based on these examples, changes can be classified in the following ways:

(i)   Slow and fast changes (ii)   Desirable and undesirable changes (iii) Periodic and non-periodic changes (iv)  Reversible and irreversible changes (v) Physical and chemical changes   (i) Slow and fast changes: Slow changes take place over days, months or years. For example, rusting of iron nails, germination of seeds, ripening of fruits, etc. Fast changes occur within a short span of time. For example, spinning of a top, burning of a matchstick, curdling of milk by adding lemon juice, etc. (ii) Desirable and undesirable changes: The changes that are beneficial or desirable for us are called desirable changes. For example formation of curd from milk, formation of manure from cow dung and dead plants. But there are some changes that may be undesirable or harmful. These are called undesirable changes. For example-the burning of a factory, flooding of a river, rotting of food stuff, etc.

• A change may be desirable at one time but undesirable at some other time. For example, the burning of a fuel (wood, coal) to produce heat is a desirable change. However burning is an undesirable change, when a house or a factory is burnt
• A change may be desirable for someone and undesirable for others. The cutting of trees may be desirable for someone who needs wood but undesirable for others because it disturbs the balance in nature.

(iii) Periodic and non-periodic changes: Changes that occur again and again after a fixed interval of time and their recurrence can be predicted are called periodic changes. For example - winter, summer, autumn, spring and rainy seasons recur each year, the waxing and waning of the moon nights recur each month, generation of high and low tides in the sea, etc. Changes that do not repeat themselves at regular intervals of time and cannot be predicted are called nonperiodic changes. For example - train accidents, the occurrence of earthquakes, landslides, sneezing, etc. (iv) Reversible and irreversible changes: If a change can be reversed, it is called a reversible change. For example, ice changes into water on heating whereas on cooling water changes back to ice. Similarly, when we put a weight on a rubber band or a spring, it stretches; but when we remove the weight, it comes back to its original shape. If a change cannot be reversed, it is called irreversible change. For example, when coal is burnt, it changes into ash and smoke and we cannot get back coal from ash and smoke. Ageing, changing of milk into curd more...

Motion, Force, and Machines MOTION

• When an object changes its position with time as compared to a stationary object, it is said to be in motion.
• In science, motions are classified as follows: (i) linear motion, (ii) random motion, (iii) circular motion, (iv) oscillatory motion.

(i)Linear motion: A bullet fired from a rifle, a boy sliding down a slope or a ball rolling on the ground or moving along a line are examples of linear motion. Note: In a linear motion, an object may move along a straight line or a curved line. (ii) Random motion: The motion of a fly, of a player on a football ground, or of a child at home are not along a fixed path. They keep on changing directions. Such motions are called random motions. (iii) Circular motion: The Moon moves around the Earth. The Earth moves round the Sun. A bull moves around a central pole. These objects move along a circular path. Such motions are called circular motions. (iv) Oscillatory motion: If a hanging object is taken to one side and then released, it starts moving like a swing. Such to-and-fro motion is called oscillatory motion.   SPEED The speed of an object can be calculated by using the relation: \[speed=\frac{Total\,\,\text{distance}\,\,travelled}{Time\,\,taken}\] Example: If a train travels 120 km in 3 hours, its speed per hour will be \[Speed=\frac{120}{3}\] \[Speed=40\,Kilometre/hour\]

• The standard unit of distance is metre and the standard unit of time is second. Therefore, the unit of speed is metre/second or m/s or \[m{{s}^{-1}}\].
• For convenience, the speed of some objects is expressed in metres/minute. Cheetah is a fast animal. It can move at a speed of 1,700 metres/minute.

  FORCE

• The push or pull applied on an object is called force. The direction in which the object is pushed or pulled is called the direction of force. The effect of force can bring three kinds of changes—

(i)   Change in speed (ii)   Change in direction (iii) Change in shape (i) Change in speed: If a force is applied in the direction of motion of the object, its speed increases and if the force is applied in the direction opposite to the direction of motion of the object, its speed decreases. For example: Hitting (applying force) a glass marble in motion with another marble from behind increases the speed of the moving marble. However, when the moving marble is hit (applied force) with another marble from the opposite direction, the speed of the moving marble decreases. (ii)Change in direction: Force can change the direction of motion of a moving object. For example: During a game of cricket, if a moving ball is hit by a bat, the direction of the ball changes; the smoke rising from an agarbatti changes its direction if we gently blow air on it. (iii) Change in shape: When a force is applied on an object, it may undergo a change in shape. more...