 Closed Circuit: When there is no gap in an electric circuit or the normal path of current has not been interrupted, the circuit is known as closed or complete circuit.
Open Circuit: When there is a gap in an electric circuit or the normal path of current has been interrupted, the circuit is known as an open circuit or incomplete circuit.
Conductors and Insulators
The substances which allow electric current to pass through them are called conductors. For example, copper, gold, silver, aluminium, iron, etc. are good conductors of electricity.
The substances which do not allow electric current to pass through them are called insulators.
For example, wood, plastic, paper, rubber, etc are insulators.
Electric Cell
An electric cell is a device which can generate electric current in a closed circuit. It is small and easily portable so it is very useful for us. There are a number of machines like watches, calculators, toys, cars, etc. in which electrical cell is used to produce electric current. Dry cell, button cell, solar cell are the examples of electric cell.
Dry Cell
A dry cell is a cylindrical device in which a number of chemicals are stored. It has a metal cap on one side called positive terminal and a metal sheet at other side called negative terminal. It produces electric current from the chemical stored inside it.
Closed Circuit: When there is no gap in an electric circuit or the normal path of current has not been interrupted, the circuit is known as closed or complete circuit.
Open Circuit: When there is a gap in an electric circuit or the normal path of current has been interrupted, the circuit is known as an open circuit or incomplete circuit.
Conductors and Insulators
The substances which allow electric current to pass through them are called conductors. For example, copper, gold, silver, aluminium, iron, etc. are good conductors of electricity.
The substances which do not allow electric current to pass through them are called insulators.
For example, wood, plastic, paper, rubber, etc are insulators.
Electric Cell
An electric cell is a device which can generate electric current in a closed circuit. It is small and easily portable so it is very useful for us. There are a number of machines like watches, calculators, toys, cars, etc. in which electrical cell is used to produce electric current. Dry cell, button cell, solar cell are the examples of electric cell.
Dry Cell
A dry cell is a cylindrical device in which a number of chemicals are stored. It has a metal cap on one side called positive terminal and a metal sheet at other side called negative terminal. It produces electric current from the chemical stored inside it.
 Electric Bulb
An electric bulb is a device which produces light energy using electrical energy. It consists of a glass bulb fixed on a metal case, a thin wire fixed between the two thick wires called filament of the bulb and the gas filled inside the glass bulb. When electric current passes through the filament, it emits light which makes the bulb glow.
Electric Bulb
An electric bulb is a device which produces light energy using electrical energy. It consists of a glass bulb fixed on a metal case, a thin wire fixed between the two thick wires called filament of the bulb and the gas filled inside the glass bulb. When electric current passes through the filament, it emits light which makes the bulb glow.
 Magnet
Magnet is a substance which attracts magnetic materials such as iron, nickel, steel and cobalt. Magnets are of different shapes and sizes. For example, U-shaped magnet, cylindrical magnet, bar magnet, etc. Each magnet has two poles, south pole and north pole.
Magnetic Materials: The materials which are attracted by a magnet are called magnetic materials. For example, iron, nickel, steel and cobalt are magnetic materials. Magnetic materials more...
Magnet
Magnet is a substance which attracts magnetic materials such as iron, nickel, steel and cobalt. Magnets are of different shapes and sizes. For example, U-shaped magnet, cylindrical magnet, bar magnet, etc. Each magnet has two poles, south pole and north pole.
Magnetic Materials: The materials which are attracted by a magnet are called magnetic materials. For example, iron, nickel, steel and cobalt are magnetic materials. Magnetic materials more... 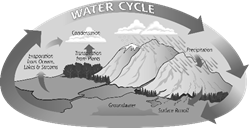 Due to sunlight water from the different sources converts into water vapor. These water vapors rise up in the atmosphere and condense to water drops forming cloud. Then they return back to the surface of earth in the form of rain.
Sources of Water
Oceans, seas, lakes, rivers, ponds, rainwater and ground water are the sources of water.
Rain Water: Rainwater is the purest form of water. It collects on the earth in the form of surface water and underground water.
Surface Water: Water present on the surface of the earth in the form of oceans, seas, rivers, lakes, ponds and streams is called surface water. Ocean contains almost 97% of water present on the earth. But it is saline therefore it is unfit for drinking.
Underground Water: Some of the rainwater seeps through the soil and gathers in the non-porous rocks below. This water is known as underground water.
Conservation of Water
As we have studied earlier water is very important for us. So we must conserve water whenever it is possible. Some ways of water conservation are:
Due to sunlight water from the different sources converts into water vapor. These water vapors rise up in the atmosphere and condense to water drops forming cloud. Then they return back to the surface of earth in the form of rain.
Sources of Water
Oceans, seas, lakes, rivers, ponds, rainwater and ground water are the sources of water.
Rain Water: Rainwater is the purest form of water. It collects on the earth in the form of surface water and underground water.
Surface Water: Water present on the surface of the earth in the form of oceans, seas, rivers, lakes, ponds and streams is called surface water. Ocean contains almost 97% of water present on the earth. But it is saline therefore it is unfit for drinking.
Underground Water: Some of the rainwater seeps through the soil and gathers in the non-porous rocks below. This water is known as underground water.
Conservation of Water
As we have studied earlier water is very important for us. So we must conserve water whenever it is possible. Some ways of water conservation are:
| Crores | Ten Lakhs | Lakhs | Ten Thousands | Thousands | Hundreds | Tens | Ones | ||||||||||||||
| 2 | 9 | 8 | more...
Fraction and Decimals
Fraction
Fraction is a method for representing the parts of a whole number. An orange is divided into two equal parts and so the first part of orange is half of the whole orange and represented by \[\frac{1}{2}\] of the orange.
Types of Fractions
Proper Fractions
A fraction whose numerator is less than denominator is called a proper fraction.
\[\frac{3}{5}\]’ \[\frac{1}{2}\]’ \[\frac{7}{9}\] are Proper fractions.
Improper Fractions
A fraction is called improper fraction even if:
LCM and HCF
LCM (Least Common Multiple)
LCM of two or more numbers is their least common multiple. LCM of 4 and 6 is 12, it means, 12 is the least common multiple of 4 and 6, therefore, 12 is exactly divisible by each of 4 and 6.
LCM by Prime Factorization Method
The following steps are used to determine the LCM of two or more numbers by prime factorisation method:
Step 1: Find the prime factors of each number.
Step 2: Product of highest power of prime factors is their LCM.
LCM by Division Method
The following steps are used to determine the LCM of two or more numbers by division method:
Step 1: Numbers are arranged or separated in a row by commas.
Step 2: Find the number which divides exactly atleast two of the given numbers.
Step 3: Follow step 2 till there are no numbers (atleast two) divisible by any number.
Step 4: LCM is the product of all divisors and indivisible numbers.
Example:
Find the least number which is exactly divisible by each of 28 and 42.
(a) 64 (b) 84
(c) 52 (d) All of these
(e) None of these
Answer (b)
Explanation: \[28=2\times 2\times 7,\,\,42=2\times 3\times 7\]
LCM =\[2\times 2\times 3\times 7=84\]
HCF (Highest Common Factor)
Highest Common Factor is also called Greatest Common Measure (GCM) or Greatest Common Divisor (GCD). H.C.F of two or more numbers is the greatest number which exactly divides each of the numbers.
HCF by Prime Factorization Method
The HCF of two or more numbers is obtained by the following steps:
Step 1: Find the prime factors of each of the given number.
Step 2: Find the common prime factors from prime factors of all the given numbers.
Step 3: The product of the common prime factors is their HCF.
HCF by Continued Division Method
The HCF of two or more numbers can also be obtained by continued division method. The greatest number is considered as dividend and smallest number as divisor.
Follow the following steps to perform the HCF of the given numbers:
Step 1: Divide the greatest number by smallest.
Step 2: If remainder is zero, then divisor is the HCF of the given number.
Step 3: If remainder is not zero then, divide again by considering divisor as new dividend and remainder as new divisor till remainder becomes zero.
Step 4: The HCF of the numbers is last divisor which gives zero remainder.
HCF of more than two Numbers
The HCF of more than two numbers is the HCF of resulting HCF of two numbers with third number. Therefore, HCF of more than two numbers is obtained by finding the HCF of two numbers with third, fourth and so on.
HCF of Larger Numbers
The HCF of smaller number (One or two digit numbers) is simply obtained by division but division of larger numbers take more more...
Ratio and Proportion
Ratio
Ratio of two quantities is the comparison of the given quantities. Ratio is widely used for comparison of two quantities in such a way that one quantity is how much increased or decreased by the other quantity.
For example, Peter has 20 litres of milk but John has 5 litres, the comparison of the quantities is said to be, Peter has 15 litres more milk than John, but by division of both the quantity, it is said that Peter has, \[\frac{20}{5}=4\] times of milk than John. It can be expressed in the ratio form as\[4:1\]
Note: In the ratio\[a:b\]\[(b\ne 0)\], the quantities a and b are called the terms of the ratio and the first term (ie. a) is called antecedent and the second term (ie. b) is called consequent.
Simplest form of a Ratio
If the common factor of antecedent and consequent in a ratio is 1 then it is called in its simplest form.
Comparison of Ratio
Comparison of the given ratios are compared by first converting them into like fractions, for example to compare \[5:6,\text{ }8:13\text{ }and\text{ }9:16\]first convert them into the fractional form
i.e. \[\frac{5}{6},\frac{8}{13},\frac{9}{16}\].
The LCM of denominators of the fractions\[=2\times 3\times 13\times 8=624\]
Now, make denominators of every fraction to 624 by multiplying with the same number to both numerator and denominator of each fraction.
Hence,\[\frac{5}{6}\times \frac{104}{104}=\]\[\frac{520}{624},\frac{8}{13}\times \frac{48}{48}\]\[=\frac{384}{624}\]and\[\frac{9}{16}\times \frac{39}{39}\]\[=\frac{351}{624}\].Equivalent fractions of the given fractions are \[\frac{520}{624},\frac{384}{624},\frac{351}{624}\]. We know that the greater fraction has greater numerator, therefore the ascending order of the fractions are, \[\frac{351}{624}<\frac{384}{624}<\frac{520}{624}\] or \[\frac{9}{16}<\frac{8}{13}<\frac{5}{6}\] or \[9:16<8:13<5:6\], thus the smallest ratio among the given ratio is \[9:16\]and greatest ratio is\[5:6\].
Equivalent Ratio
The equivalent ratio of a given ratio is obtained by multiplying or dividing the antecedent and consequent of the ratio by the same number. The equivalent ratio of \[\text{a}\,\,\text{:}\,\,\text{b}\] is \[\text{a}\,\times \,\text{q}\,\,\text{:}\,\,\text{b}\,\times \,\text{q}\]whereas, a, b, q are natural numbers and q is greater than 1.
Hence, the equivalent ratios of \[5:8\]are, \[\frac{5}{8}\times \frac{2}{2}=\frac{10}{16}\] or\[10:16\], \[\frac{5}{8}\times \frac{3}{3}=\frac{15}{24}\] or\[15:24\], \[\frac{5}{8}\times \frac{12}{12}=\frac{60}{96}\] or\[60:96\].
Example: Mapped distance between two points on a map is 9 cm. Find the ratio of actual as well as mapped distance if 1 cm = 100 m.
(a) \[10000:1\] (b) \[375:1\]
(c) \[23:56\] (d) \[200:1\]
(e) None of these
Answer (a)
Explanation: Required ratio =\[900\times 100:9=\]
\[90000:9=10000:1\]
Example: Consumption of milk in a day is 6 litre. Find the ratio of Consumption of milk in month of April and quantity of milk in a day?
(a) \[99:2\] (b) \[30:1\]
(c) \[123:3\] (d) \[47:3\]
(e) None of these
Answer (b)
Explanation: Required ratio \[=30\times 6:6=30:1\]
Proportion
The equality of two ratios is called proportion. If a cake is distributed among eight boys and each boy gets equal part of the cake then cake is said to be distributed in proportion. The simplest form of ratio \[12:96\]is \[1:8\]and\[19:152\]is \[1:8\]therefore, \[12:96\]and \[19:152\] are in proportion and written as \[12:96::19:152\]or more...
Geometry and Symmetry
Basic Geometrical Shapes
Lines and angles are the main geometrical concept and every geometrical figure is made up of lines and angles. Triangles are also constructed by using lines and angles.
Point
A geometrical figure which indicates position but not the dimension is called a point. A point does not have length, breadth and height. A point is a fine dot. P is a point on a plane of paper as shown below.
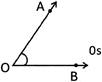 Vertex or common end point is O.
OA and OB are the arms of \[\angle AOB\]
The name of the above angle can be given as \[\angle AOB\]or \[\angle BOA\]
The unit of measurement of an angle is degree\[({}^\circ )\]
Types of Angles
Acute Angle
The angle between \[0{}^\circ \] and \[90{}^\circ \] is called an acute angle.
For example, \[10{}^\circ ,\,\,30{}^\circ ,\,\,60{}^\circ ,\,\,80{}^\circ \]are acute angles.
Right Angle
An angle of measure \[90{}^\circ \] is called a right angle.
Obtuse Angle
An angle whose measure is between \[90{}^\circ \] and \[180{}^\circ \] is called an obtuse angle.
Straight Angle
An angle whose measure is \[180{}^\circ \,\,\text{is}\]called a straight angle.
Vertex or common end point is O.
OA and OB are the arms of \[\angle AOB\]
The name of the above angle can be given as \[\angle AOB\]or \[\angle BOA\]
The unit of measurement of an angle is degree\[({}^\circ )\]
Types of Angles
Acute Angle
The angle between \[0{}^\circ \] and \[90{}^\circ \] is called an acute angle.
For example, \[10{}^\circ ,\,\,30{}^\circ ,\,\,60{}^\circ ,\,\,80{}^\circ \]are acute angles.
Right Angle
An angle of measure \[90{}^\circ \] is called a right angle.
Obtuse Angle
An angle whose measure is between \[90{}^\circ \] and \[180{}^\circ \] is called an obtuse angle.
Straight Angle
An angle whose measure is \[180{}^\circ \,\,\text{is}\]called a straight angle.
 Vertically more...
Vertically more...
Mensuration
Perimeter and Area of Plane Figures
Perimeter of geometrical figure is the sum of its sides. There are different types of geometrical figures. Figures are classified by their shapes and sizes. Area of a geometrical figure is its total surface area.
Perimeter and Area of a Triangle
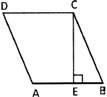 Perimeter of a Parallelogram = 2 (sum of two adjacent sides)
Hence, perimeter of a parallelogram \[\text{ABCD=2(AB+BC)}\]Area of a parallelogram = Base \[\text{ }\!\!\times\!\!\text{ }\] Height
Therefore, the area of a parallelogram \[\text{ABCD=AB }\!\!\times\!\!\text{ CE}\]
Perimeter and Area of a Rectangle
A rectangle has four right angles and its opposite sides are equal.
Longer side of a rectangle is called length and shorter side is called width.
Perimeter of a Parallelogram = 2 (sum of two adjacent sides)
Hence, perimeter of a parallelogram \[\text{ABCD=2(AB+BC)}\]Area of a parallelogram = Base \[\text{ }\!\!\times\!\!\text{ }\] Height
Therefore, the area of a parallelogram \[\text{ABCD=AB }\!\!\times\!\!\text{ CE}\]
Perimeter and Area of a Rectangle
A rectangle has four right angles and its opposite sides are equal.
Longer side of a rectangle is called length and shorter side is called width.
 Perimeter of rectangle
\[ABCD=AB+BC+CD+DA\]
= length + width + length + width = 2(length + width)
Hence, perimeter of a rectangle = 2(length + width)
Area of a rectangle = length \[\times \]width
Perimeter and Area of a Rhombus
A rhombus is a parallelogram with four equal sides.
Therefore, perimeter of rhombus\[=4\times side\]. In the figure given below ABCD is a rhombus.
Perimeter of rectangle
\[ABCD=AB+BC+CD+DA\]
= length + width + length + width = 2(length + width)
Hence, perimeter of a rectangle = 2(length + width)
Area of a rectangle = length \[\times \]width
Perimeter and Area of a Rhombus
A rhombus is a parallelogram with four equal sides.
Therefore, perimeter of rhombus\[=4\times side\]. In the figure given below ABCD is a rhombus.
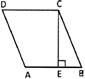 Perimeter of a rhombus, \[=4\times side\]
Area of a rhombus = base \[\times \] height
Also area of a rhombus \[\text{=}\frac{1}{2}\times \] product of length of diagonals.
Perimeter and Area of a Square
A square has four equal sides and each angle of\[90{}^\circ \].
In the picture given below, ABCD is a square because its all sides are equal and each angle is a right angle.
Perimeter of a rhombus, \[=4\times side\]
Area of a rhombus = base \[\times \] height
Also area of a rhombus \[\text{=}\frac{1}{2}\times \] product of length of diagonals.
Perimeter and Area of a Square
A square has four equal sides and each angle of\[90{}^\circ \].
In the picture given below, ABCD is a square because its all sides are equal and each angle is a right angle.
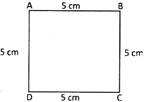 Perimeter of square = side + side + side + side\[=4\times side\]
Area of a Square = side \[\times \]side = \[{{(side)}^{2}}\]
Perimeter and Area of a Trapezium
A quadrilateral whose one pair of sides are parallel is called a trapezium. The given figure is a trapezium in which parallel sides are AB and CD and non-parallel sides are AD and BC
Perimeter of square = side + side + side + side\[=4\times side\]
Area of a Square = side \[\times \]side = \[{{(side)}^{2}}\]
Perimeter and Area of a Trapezium
A quadrilateral whose one pair of sides are parallel is called a trapezium. The given figure is a trapezium in which parallel sides are AB and CD and non-parallel sides are AD and BC
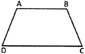 Perimeter of a trapezium = Sum of the length of all sides
Area of a trapezium \[=\frac{1}{2}\times \] (Sum of lengths of parallel sides) \[\times \]distance between parallel sides.
Cirumference and Area of a circle
A round plane figure whose all points are equidistant from a fixe point is called a circle and the fixed point is called centre of the circle more...
Perimeter of a trapezium = Sum of the length of all sides
Area of a trapezium \[=\frac{1}{2}\times \] (Sum of lengths of parallel sides) \[\times \]distance between parallel sides.
Cirumference and Area of a circle
A round plane figure whose all points are equidistant from a fixe point is called a circle and the fixed point is called centre of the circle more...
Data Handling
In this chapter we will learn about pictograph and bar graph.
Data
Data is a collection of facts, such as numbers, observations, words or even description things.
Observation
Each numerical figure in a data is called observation.
Frequency
The number of times a particular observation occurs is called its frequency.
Statistical Graph
The information provided by a numerical frequency distribution is easy to understand when we represent it in terms of diagrams or graphs.
To represent statistical data, we use different types of diagrams or graphs. Some of them are:
(i) Pictograph
(ii) Bar graph
Pictograph
A pictograph represents the given data through pictures of objects. It helps to answer the questions on the data at a glance.
Example:
The following pictograph, shows the number of cakes sold at a bakery over five days.
| ||||||||||||||||||