Current Affairs 6th Class

The Living World  

• There is a variety of living organisms around us. Each one of them possesses a definite shape, size, structure and a colour pattern Similarly, things like living places (water and land), home (nests holes of trees), food habits, etc., give each organism a different identity.
• Each kind of organism has many individuals. There are differences and similarities among the individuals of a kind based on which they can be recognised.
• The individuals of a kind have a similarity in their body parts and their functioning. They eat the same kind of food and live in the same habitat. They cooperate among themselves for reproduction. Such a group of similar individuals is known as species. Each species has a name.
• Each plant and animal has a scientific name consisting in two words. These scientific names help us in identifying each type of plant or animal and the group to which it belongs. When they are written the first letter of the first word (group name) is always written as a capital letter, but the first letter of the second word (individual name) is written as a small letter.

 

Example — Scientific names and their writing pattern
Indian Tiger	Panthera tigris
Indian Peafowl	Pavo cristatus
Man	Homo Sapines
Mango	Manifera indica

  Note: Although in different languages the plants and the animals may be called by different names, their scientific names are the same all over the world.

• Living organisms are very different in shape, size, habitat, food habits and behaviour. They breathe in different ways and move around in different ways. They even have different ways of growing and reproducing themselves. All have different names but despite all these differences, they all have one most important thing in common—they are all living.
• The living organisms share some features with the non-living objects. All living and non-living objects are made of matter. They all have mass and occupy space. But life is the process seen only in living objects in the form of growth, movement, feeding or eating, sensitivity, respiration, excretion and reproduction.
• The world of living organisms can be divided into two groups:

(i) plants and (ii) animals.

• An important difference between plants and animals is the way they obtain their food. Most animals, being able to move around, obtain food by looking for and going after it. However, most plants are fixed. They manufacture their own food. The process by which they manufacture their food is called photosynthesis.
• Plants and animals reproduce themselves. They produce one or more individuals of their own kind. Plants reproduce mainly through seeds or spores. Certain plants reproduce through leaves, for example, Bryophyllum. Some also reproduce through stems, like ginger, potato. Animals reproduce by laying more...

Air  

• Air is everywhere around us. No living being can survive without air.
• The air covers the whole Earth. This cover of air is called the atmosphere. We live within the atmosphere. It extends over hundreds of kilometres. Up to a height of 16 km, we find clouds, rain and snow. As we go up in the atmosphere, there is less and less air. Jet planes usually fly above the clouds.
• Air is matter. It occupies space and has mass. It has no colour and we can see through it. It fills all the space available to it.
• Air is a mixture of several gases. Nearly fourth-fifths (4/5) of it is nitrogen. About one-fifth (1/5) of it is oxygen. Air also has a small amount of carbon dioxide, argon, helium, water vapour and dust particles.
• At higher altitudes, air is thin and under the water, the available oxygen is less. Thus, breathing becomes difficult. Therefore, mountaineers and divers carry cylinders containing oxygen with them. Oxygen is also supplied to the patients who suffer from breathing difficulties.
• Oxygen is used by living organisms for respiration. During respiration, oxygen breaks down the food to release energy. During this process, carbon dioxide and water vapour are produced and released.
• Carbon dioxide along with water is used by the green plants in the presence of sunlight to make their food. This process is called photosynthesis. During this process, oxygen is released. In nature, the balance of oxygen and carbon dioxide is, thus, maintained.

  AIR IS USEFUL TO HUMAN BEINGS

• Air is required by human beings for respiration.
• Air is necessary for burning. A chulha, sign or kerosene stove burn only when sufficient air is available.
• Vehicles such as bicycles, few kinds of carts, scooters, cars, trucks and aeroplanes have tyres filled with compressed air. Such tires make transport smooth and easier.
• Balls used for playing and balloons can be used only when they are inflated with air.
• Compressed air is used in machines for digging, mining and breaking stones. It is also used for lifting liquid substances from a mine.
• Compressed air is used in the brake systems of trains.
• Air helps in drying agricultural products such as grains, pulses, dry fruits and wet clothes.
• People feel cool in summer under a fan. The fan circulates air. This helps in rapid evaporation of sweat.
• Air helps in the movement of sail boats, gliders, parachutes and aircraft. Birds, bats and insects fly in the air.
• Air makes a windmill move. A windmill is used to draw water from tube wells and to operate flour mills. Along the coast, windmills are used to generate electricity.

   

Water   Water is the most common and important substance around us. Water is essential for almost every task we perform on a daily basis as well as for agriculture and industries.

• All animals and plants need water. The human body has about 70 percent water by weight. Similarly the elephants and plants have 80 percent and 60 per cent water by weight respectively.
• Animals drink water from ponds, streams and rivers. Plants take in water from the soil through their roots. From the roots, it goes to different parts of the plant. The plant uses this water for its life processes. It also loses water continuously from the tiny openings in the leaves. The process is called transpiration.
• Seeds cannot germinate without water. Water helps animals in releasing heat which maintains their body temperatures.
• A villager in India uses about 12 litres of water every day. In cities, a person uses 50-2000 litres of water every day. With the rising living standards, the requirement of water has also increased.
• Large amounts of water are consumed in agricultural activities. Many industries such as paper, rayon, petroleum refining, fertiliser, dye, drug and chemical industries require large quantities of water.
• In some countries, people use water to warm their houses. It is used to keep things cool. A car radiator is filled with water to keep the engine cool.
• The largest amount of water on the Earth is in oceans. The oceans cover more than two-thirds (2/3) surface area of the Earth. Seawater is salty and cannot be used at home and in agriculture. So, we depend upon other sources of water like springs, rivers, lakes, ponds, wells, rain, snow and underground water. Water obtained from these sources is not always fit for drinking and cooking purposes. Many impurities and germs may be present in it.
• Various methods are used to make this impure water fit for drinking. People in cities get pure water from taps. This impure water travels a long way to reach the taps. In many cases, water is first pumped from a source, such as a river or lake, and collected in a reservoir. Then it goes to the waterworks where it is cleaned. Here, it is filtered through layers of gravel and sand. The dirt stays behind in the sand, then water is treated with some chemicals like chlorine to kill the germs. The clean water is supplied through main pipes to different parts of the city. Smaller pipes take the water to each house.

At places where tap water is not available, people draw out water from rivers, lakes, springs and wells. Water from these sources should be made fit for use by boiling, filtering and treating it with some chemicals such as potassium permanganate.    

• Pure water is colourless, odourless, tasteless and transparent. Small quantities of dissolved salts and gases give a pleasant taste to water. Water from the wells, more...

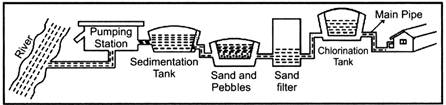
States of Matter  

• We see a variety of objects around us. Generally, all objects are classified into three categories:

(i)   Solids (stone, wood, iron, etc.) (ii)   Liquids (water, oil, milk, etc.) (iii) Gases (oxygen, air, vapour, etc.)

• Water can exist in all the three forms—solid, liquid, gas.
• Solids and liquids have surfaces but gases do not have surfaces.

• Liquids need a container to kept it, otherwise they tend to flow. On the other hand solids can be heaped anywhere.
• All matters are made up of tiny particles called molecules. Molecules are constantly moving about. The higher the temperature, the greater is their motion. Also, when two molecules come closer they tend to stick together because there is a weak force of attraction between them.
• The movement of molecules in solids, liquids and gases has been described:

  Solids: In a solid, the intermolecular forces are so strong that molecules cannot slip away. They are kept together in order and are not allowed to move much. This makes it clear why solids melt on heating and liquids turn into gases when heated. Also, when a gas is cooled, its molecules slow down and eventually condense into a liquid.   Liquids: In a liquid, the molecular motions are not great enough to overcome the force of attraction between the molecules. This is why, the molecules tend to stay together and give a condensed form. However, these forces are not strong enough to prevent the liquid from flowing.   Gases: In a gas, molecules are moving fast. They overcome the molecular force of attraction and move in all directions. This is why, a gas keeps expanding until it fills all the available space.    

Electricity   Charge

• Charge is the fundamental quantity of electricity.
  • The classical study of electricity is generally divided into many areas:
• Electrostatics: It deals with phenomena due to attractions or repulsions of electric charges but not dependent upon their motion.
• Electric Current: The study of the forms of energy associated with the flow of electric charge.
• Electromagnetism: The study of the forces acting between electrically charged particles in motion.
• Electric Charge: (Often just called charge) It is of two types, i.e. positive (+) and negative \[\left( - \right)\] charges.
• The term neutral does not refer to third type of charge, but to the presence in a region of positive and negative charges in equal amount.

  Methods of Charging

• Friction: The frictional charging process results in a transfer of electrons between the two objects that are rubbed together.
• Conduction: It involves touching a negatively charged object to a neutral object. Upon contact, electrons move from the negatively charged object to the neutral object.
• Induction: If a negatively charged object is used to change a neutral object by induction, then the neutral object will acquire a positive charge and vice-versa.

  Electrical Properties of Materials

• Conductors: Charge moves easily through
• Metals
• Electrolytes (ionised liquids)
• Plasmas (ionised gases)
  • Insulators: Charge does not move easily through
• Non-metals (pure water, organics, gases, ...)
• Semiconductors: Sometimes behave as a conductor and sometimes as an insulator.
• Metalloids (silicon, germanium, doped metals, ...)
  • Superconductors: The perfect conductor that offers no resistance below critical temperature.
  • Many substances become superconductors when they are below some critical temperature.
  • The SI unit of charge is the coulomb (C).

  Coulomb's Law The force between two point charges is directly proportional to the product of magnitude of each charge \[\mathbf{(}{{\mathbf{q}}_{\mathbf{1}}}\mathbf{,}\,{{\mathbf{q}}_{\mathbf{2}}}\mathbf{)}\] and inversely proportional to square of the separation between their centres (r) and directed along the line connecting their centres (r’). This relationship is known as Coulomb's Law.   Electric Current

• Electric current is the rate at which charge flows through a surface.
  • As a scalar quantity it has magnitude only.
  • The symbol for current is I.
• The SI unit of current is the ampere (A) which is named after the French scientist Andre-Marie Ampere.
• Since charge is measured in coulombs and time is measured in seconds, an ampere is the same as a coulomb per second.

Q = It I = Ampere Q = Coulomb t = Second   Resistance

• Resistance is the property of a conductor to resist the flow of charges through it. Its SI unit is ohm \[(\Omega )\].
• Resistivity is a characteristic property of the material. It is a measure of material's ability to oppose electric current. Its SI unit is \[\Omega -M\] (ohm-metre).
• Resistivity depends on the nature of the material not on its dimensions as resistance.

Resistance\[(R)\,=\,\rho \frac{L}{A}\] where    \[\rho =\]resistivity of more...

Magnet  

• A magnet is an object or a device that gives off external magnetic field.
• Basically, it applies a force over a distance on other magnets, electrical currents, beams of charge, circuits, or magnetic materials.
• The magnetic field of an object can create a magnetic force on other objects with magnetic fields. That force is what we call magnetism.
• When a magnetic field is applied to a moving electric charge, such as a moving proton or the electrical current in a wire, the force on the charge is called Lorentz force.
• Magnets have two poles, called the north (N) and south (S) poles. Two magnets will be attracted by their opposite poles, and each will repel the like pole of the other magnet.
• Repulsion: When two magnetic objects have like poles facing each other, the magnetic force pushes them apart.
• A magnetic field consists of imaginary lines of flux coming from moving or spinning electric circuit.
• Examples include the spin of a proton and the motion of electrons through a wire in an electric circuit.
• Magnets also strongly attract Ferro-magnetic materials such as iron, nickel and cobalt.

  Magnetism

• A magnetic field consists of imaginary lines of flux coming from moving or spinning electrically charged particles. Examples include the spin of a proton and the motion of electrons through a wire in an electric circuit.
  • Magnetism is the force exerted by magnets when they attract or repel each other. Magnetism is caused by the motion of electric charges.
• In most substances, equal numbers of electrons spin in opposite directions, which cancel out their magnetism. That is why materials such as cloth or paper are said to be weakly magnetic. In substances such as iron, cobalt and nickel, most of the electrons spin in the same direction. This makes the atoms in these substances strongly magnetic, but they are not yet magnets.
• A magnet is an object that exhibits a strong magnetic field and will attract materials like iron to it. Magnets have two poles, called the north (N) and south (S) poles. Two magnets will be attracted by their opposite poles and each will repel the like pole of the other magnet.

  Magnetic field

• A magnetic field consists of imaginary lines of flux coming from moving or spinning electrically charged particles. Examples include the spin of a proton and the motion of electrons through a wire in an electric circuit.

 

  Motion and Measurement of Distances   Synopsis    

• Different modes of transport are used to go from one place to another.

 

• In ancient times, people used the length of a foot, the width of a finger, the distance of a step as units of measurement. This caused variation and inaccuracy and a need to develop a uniform system of measurement arose.

 

•  Now, the International System of Units (S.I. unit) is followed all over the world.

 

• A unit is a standardized quantity of a physical property, used as a factor to express quantities of that property.

 

•  A standard unit is the measurement value which remains the same even when it is measured by anybody at any place.

 

• The standard units of length are millimetre (mm), centimetre (cm), metre (m) and kilometer (km).

 

• The following is the relationship between the units.

\[10\text{ }mm=1\text{ }cm\] \[100\,\,cm=1\text{ }m\] \[1000\text{ }m=1\text{ }km\]        

• The correct technique of measuring length is the eye being directly in line with the other end of the object as shown in the adjacent figure.

 

•  A thread or string and a ruler are used for measuring the length of a curved line and the circumference of a ball.

  Types of motion

•   Motion in a straight line is called rectilinear motion.

 

• A man walking and the motion of a cycle, a bus and that of a car on a straight path are all in translatory motion.
• If the motions of points or parts of an object are along a circular path instead of a straight line path/then the motion of the body is said to be in rotatory motion.

 

• The to and fro motions of an object about a fixed point is called oscillatory motion.

 

• Oscillatory motion which is very fast to begin with and soon slows down and comes to rest is called vibratory motion.

       

Light, Shadows and Reflection   Synopsis    

• Objects which emit light energy by themselves are called luminous bodies.

          e.g., the sun, the stars, and glow worms.

•  The bodies which do not have light energy of their own but reflect the light energy falling on them and hence are visible to us are called non-luminous bodies.

         e.g., the moon, objects around us, books, chairs, buildings, trees, etc.  

• The moon appears bright due to the reflection of sunlight falling on it.

 

• Transparent bodies are substances through which light is propagated easily,

          e.g., glass/water/etc.  

• Translucent bodies are substances through which light is propagated partially.

          e.g., oil, ground glass, etc.  

• Opaque bodies are substances through which light is not propagated.

         e.g., wood, iron, etc.  

• Light travels in straight lines.

 

• Smooth surfaces like mirrors form images.

 

• The shadow of an object is formed because of the rectilinear propagation of light. A shadow is the area of darkness formed on the screen, when an opaque body is placed in between the screen and a source of light

 

• A pin hole camera uses the principle of rectilinear propagation of light. It produces a real image which is much smaller than the object and is inverted (upside down).

       

•  The returning of a light ray passing through an optical medium into the same medium from the surface of the second medium is called the reflection of light.

 

• The surfaces which reflect light are called reflecting surfaces.
•  Images are different from shadows.

Electricity and Circuits   Synopsis  

• Electricity is a form of energy widely used by man.

 

• The simplest form of a circuit is when the two terminals of a cell are connected to the two terminals of a bulb through a switch.

 

• In an electric circuit/the direction of current is taken from the positive terminal to the negative terminal of the source.

 

• When a circuit is complete, current (charges) starts flowing. It stops flowing when the circuit breaks at a point.

 

• A switch is used to break or complete a circuit.

 

• Materials that allow electricity to pass through them are called conductors. Most of the metals and impure water are examples of conductors.

 

• Materials that do not allow electricity to pass through them are called insulators. Dry wood, pure water, air and rubber are examples of insulators.

 

• To represent an electric circuit certain symbols are being used. A list of few symbols are given below in the table.

   

Circuit components	Symbols
Cell
Battery
Tap key
more... Catgeory: 6th Class Fun with Magnets Fun With Magnets   Synopsis   Substances that can attract iron are called magnets.   Substances can be divided into magnetic and non-magnetic substances.   Substances that are attracted by a magnet are called magnetic substances. Usually things made up of iron, nickel or cobalt are magnetic.   Substances that are not attracted by a magnet are called nan-magnetic substances. Paper, plastic and wood are a few examples of non-magnetic substances.   Magnets are divided into two groups - natural and artificial magnets. Magnetite (lodestone) is a naturally occurring magnet.   Artificial magnets can be of many shapes and are commonly used in different articles like electric bells, radio, etc.   The magnetic force or the force of attraction in a magnet is concentrated at the two ends of a magnet. These ends are called poles. They are called the north pole and the south pole.   Properties of magnets          (i) There are always two poles in a magnet placed at opposite ends. This holds true even if we break or cut the magnet into      smaller pieces. Each piece           will have two poles.          (ii) When two different magnets are brought closer, like poles repel and unlike poles attract each other.          (iii) A magnet, when suspended freely, always comes to rest in a line along the north-south line of that place.   The bar AB (of iron or steel) to be magnetized is stroked with a bar magnet from one end to the other using the same pole as shown in the figure. This process is repeated for about 50 times.     The end A from where the process starts develops the same polarity as the pole of the magnet stroking and the other end develops the opposite polarity.   Magnets lose their properties when they are heated, hammered or dropped and if they are not stored properly.   Magnetism is widely used to make articles like cassettes, computers, T.V., ATM cards, etc. Catgeory: 6th Class Current Affairs Categories National International Agreements Appointments Government Schemes Summits Awards & Honours Business Economy & Banking Defense Sports Ranks & Reports Important Days Persons Science & Technology State Environment Bills & Acts Schemes Miscellaneous Archive August 2020(12) February 2020(215) January 2020(211) July 2020(35) June 2020(143) March 2020(99) May 2020(49) April 2019(263) August 2019(324) December 2019(331) February 2019(280) January 2019(306) July 2019(359) June 2019(231) March 2019(259) May 2019(258) November 2019(228) October 2019(222) September 2019(322) April 2018(298) August 2018(290) December 2018(292) July 2018(306) June 2018(311) March 2018(5) May 2018(328) November 2018(277) October 2018(276) September 2018(281) Trending Current Affairs Smart Cities India 2018 Expo Underway In New Delhi CII Pegs India's GDP Growth At 7.3-7.7% For 2018-19 World Environment Day 2018 Celebrated In New Delhi President 3-Nation Visit: India & Cuba Sign MoUs SCM BrahMos Test Fired Under Extreme Conditions 4 Indian-Origin Names In List Of Fortune's 40 Young Influential People Colombia joins NATO as global partner Bangladesh Cabinet Clears Deal With India For Port Usage PM Inaugurates Key Development Projects In Varanasi Paisabazaar.com Launches India’s First ‘Chance of Approval’ Feature Please Wait you are being redirected.... You need to login to perform this action. You will be redirected in 3 sec × Reset Password. Email : Send Password Cancel Add Mobile Enter Mobile Number Submit Logout Enter OTP OTP has been sent to your mobile number and is valid for one hour Enter One Time Password Submit Change Mobile: Submit Logout Mobile Number Verified Your mobile number is verified. Close Free Videos × For free video lectures fill in the form below and we will get back to you. * Email Address: * Mobile Number: Submit Cancel