| Object | Subject | Object | Subject | |||||||||||||||||||||||||||||||||||||||
| me | I | you | you | |||||||||||||||||||||||||||||||||||||||
| her | she | them | more...
Tenses
Tenses tell us about past, present and future.
Let us look at some examples to recognise the tenses.
Past Tense
1.
Gopal loved Sita.
2.
Rama was jumping in the garden.
3.
We had gone to the market yesterday.
4.
I had been painting the wall for two hours.
In these sentences, second form of verb, was, had etc.,
shows the past tense.
To recognise the past tense, we have to see the helping
verb in the sentence as underlined in the above sentences.
Present Tense
1.
Gopal loves Sita.
2.
Rama is jumping in the garden.
3.
They are playing.
4.
We have gone to the hospital.
5.
She has gone to the market.
6.
I have been painting the wall for two hours.
Future tense
1.
Gopal will love Sita.
2.
Rama will be jumping in the garden.
3.
I shall be playing in the garden.
4.
We shall have gone to the market.
5.
She will have gone to the hospital.
6.
I shall have been painting the walls for two months.
In the above examples you recognise the tense by
recognising the underlined helping verbs related to concerned tenses.
Conjunction
Conjunctions are words which join two sentences or two
words. Actually, you can say the conjunctive words act as a bridge in between two
sentences or words or numbers.
·
Example 1
1.
Entire world is made up of tiny particles and we are the part of
this.
2.
Two boys and three girls make five people.
3.
To say anything is easy but its implementation is hard.
4.
Do or die.
So, you can define conjunction as
follows:
The words which join two sentences or words or number.
The words, 'and, but, or' are the conjunctive words.
But you must give attention that conjunction must be
carefully distinguished from the relative pronouns, relative adverbs and
prepositions which are connecting words.
·
Example 2
1.
This is the building that the contractor built.
2.
This is the house where Ram lived.
3.
Go there and get the packet.
These three sentences use relative pronouns, relative
adverbs and conjunctions. In the first sentence ?that? is the relative pronoun
which joins both the parts of the sentence. In the second sentence relative
adverb 'where' modifies the verb and joins the two parts of the sentence. In
the third sentence ?and? is the conjunction which joins the two parts of the
sentence.
Actually the conjunction merely joins the two sentences while
in case of relative pronouns, and relative adverb etc., they do more.
Some other words used as conjunctions
in pairs:
1.
Either - or
? Either go away or sit down.
2.
Neither - nor
? Neither win nor lose.
3.
Both - and
? We both lay on bed and sleep.
4.
Though - yet
? Though he was feeling bad yet he never expressed.
5.
Whether - or
? I do not bother whether he stays or
not
6.
Not only - but also
? Not only men but also women can join
army
Classification of Conjunction
There are two types of conjunction
1.
Coordinating conjunction
2.
Subordinating conjunction
Coordinating Conjunction:
Those conjunctions which join two statements of equal
rank. For example:
? Earth is moving around the Sun and Moon is moving around
the Earth.
Types of coordinating conjunction
(a) Cumulative or Copulative
It merely adds one statement to another. For example:
? We carved not a line and we raised
not a stone.
(b) Adversative
It more...
Preposition
A
preposition is a word placed before a noun or a pronoun to show the relation of
a person of a thing with something else. For example: in, of, off, etc.
There
is a cow in the field.
?In?
shows the relation between the cow and the field.
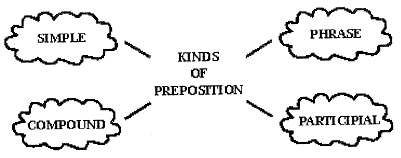1.
Simple Prepositions:
Which shows simply the relation of a person or thing with
something else. For example: at, by, from
2.
Compound Preposition:
It is generally formed by prefixing a preposition to a
noun, an adjective or an adverb. For example: about, behind, underneath
3.
Phrase Prepositions:
They are the groups of words used as a single preposition.
For example: in accordance with, in place of
4.
Participle Prepositions:
The words which are similar to present participles of
verbs are sometimes used as prepositions, they are called participle
prepositions. For example: barring, concerning, etc.
Concering (= about) yesterday?s fire, there are many
rumours in the bazar.
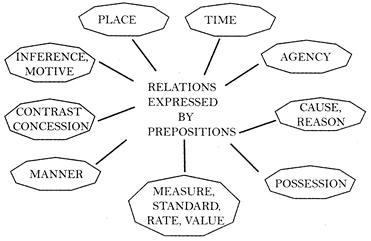1.
Place
For example:
Went around the world.
Ran across the road.
2.
Time
For example:
After his death.
In the afternoon.
3.
Agency
For example:
Cut it with a knife.
He was stunned by a blow.
4.
Cause, Reason
For example:
Died from fatigue.
Took medicine for cold.
5.
Possession
For example:
There was no money on him.
A man of means.
6.
Measure, Standard, Rate, Value
For example:
I am taller than you by two inches.
7.
Manner
For example:
Fought with courage.
Won with ease.
8.
Contrast, Concession
For example:
After every effort.
9.
Inference, Motive
For example:
Light emanates from the sun.
Special Uses of Prepositions
1.
Use ?in or at? with names of cities, town or village.
For example: We stayed in Mumbai./We stayed at Mumbai.
2.
Use ?at or to? talk about group activities and shops.
For example: I saw him at the baker?s.
3.
Use ?in? with the names of streets and ?at? with house number
For example: He lives in Tanga street
at house no. 17.
4.
Use ?on? when think of a place as a surface.
For example: The dog is lying on the
floor.
5.
?Till? is used for time and ?to? is used for place.
For example: He slept till eight o?
clock.
6. more...
Adverb
The
word that modifies the verb is called adverb.
For
example: quickly, very, etc.
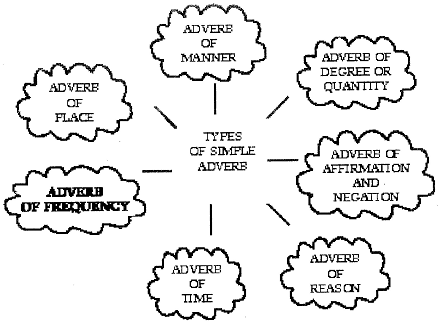1.
Adverb of Manner:
It shows how or in what manner.
For example:
Rama sleeps soundly.
The girl works hard.
2.
Adverb of Degree or Quantity:
It shows how much or in what degree.
For example:
He is too careless.
I am so glad.
3.
Adverb of Affirmation and Negation:
It shows confirmation.
For example:
He certainly went to Bhopal.
I do not know him.
4.
Adverb of Reason:
It shows the reasoning.
For example:
He therefore left home.
5.
Adverb of Time:
It shows when the verb takes place.
For example:
Wasted time never returns.
She comes to school daily.
6.
Adverb of Frequency:
It shows how often.
For example:
She often makes mistakes.
He seldom comes here.
7.
Adverb of Place:
It shows where.
For example:
My mother is out.
The horse runs away
Interrogative Adverb:
The adverb which is used to ask questions is called
interrogative adverb.
For example:
When did you come?
(Interrogative adverb of time)
Where is Rahul?
(Interrogative adverb of place)
Relative Adverb:
The adverb which relates back to its antecedent sentence
is called relative adverb.
For example:
This is the reason why I left.
How to Compare Adverbs?
Some adverbs, like adjectives, have three degrees of
comparison positive, comparative and superlative.
Fast Faster Fastest
Formation of Adverb:
Mostly adverbs are the compound of noun, compound of
preposition and adjective, compound of preposition and adverbs and are derived
from pronouns, e.g.
a bed (on bed) (compound of Noun)
abroad (compound
of preposition and adjective)
without (compound
of preposition on and adverb)
there (derived
from pronoun)
Some adverbs are formed by adjectives.
For example: beautifully happily
sometimes, etc.
Uses of Adverb:
1.
Adverb of manner is used generally after the verb or after the
object.
For example: It is raining heavily
2.
Adverb of place and of time after the verb or object.
For example: I met him yesterday
3.
Adverb of frequency used between the subject and the verb.
For example: His wdfe never cooks.
4.
Adverbs are usually put before an auxiliary or the single verb ?be?.
For example: Do you eat meat? Yes, I sometimes do.
5.
When an adverb modifies an adjective or another adverb, the adverb
usually comes before it.
For example: Rama is rather a lazy
girl.
6.
But more...
Verb
Verb is a word or group of words
that expresses action. feeling or existence.
1.
Intransitive Verb:
The verb that does not need any
object to make a sentence meaningful is called intransitive verb.
For example:
Ram writes.
Neetu plays.
2.
Transitive Verb:
The verb that needs an object to
make a meaningful sentence is called transitive verb.
For example:
Neetu plays
lawn tennis.
Nita loves
me.
(a) Transitive Verb
with Two Objects
There are two
objects with transitive verbs:
A person and
a thing
The person is an indirect and
the thing is a direct object.
For example:
Mr. Sharma
teaches us Hindi.
He told us
about an incident.
If direct object comes before
indirect object, then we have to use ?to? or ?for? before indirect object.
For example:
I bought a
bouquet for my mother.
(a) Transitive
Verb with Object and Complement
There is a complement with
object in the sentence.
For example:
He offered
her (object) a book (complement).
3.
Linking Verb:
The verb that needs a complement
to make a meaningful sentence is called linking verb.
(a)
Subjective Complement:
The
complement describes subject.
For example:
The soup is
hot.
Hot describes
the soup (subject).
(b)
Objective Complement:
The
complement describes object.
For example:
They chose
Mr. Khanna, their leader.
Leader describes Mr. Khanna (object).
4.
Auxiliary Verb:
Auxiliary verbs are the helping verbs which help the main
verb in tense, mood or voice.
For example: has, have, shall, is, are, am
I had opened the door
All the verbs have three forms.
| |||||||||||||||||||||||||||||||||||||||
1.
